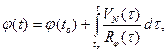Обобщенное уравнение пуассона для бинс

Алгоритм идеальной работы автономных БИНС

УТВЕРЖДАЮ

Директор ЦНИИ «Электроприбор»

Академик РАН

В.Г. Пешехонов

«_____»__________________2013 г.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по проведению в учебном центре ЦНИИ «Электроприбор» лабораторной работы

Имитационное моделирование алгоритма работы бесплатформенной инерциальной навигационной системы

Цель работы

Целью данной работы является имитационное моделирование алгоритмов идеальной работы автономной бесплатформенной инерциальной навигационной системы (БИНС) и изучение влияния точностных характеристик ее чувствительных элементов на погрешность выработки кинематических параметров.

Целью работы является также ознакомление с методами нелинейного динамического моделирования в пакете Simulink.

Общие сведения

Сутьинерциального метода навигации заключается в интегрировании в реальном масштабе времени дифференциальных уравнений поступательного движения ц.м. подвижного объекта. В качестве исходной информации (первичных навигационных измерений) здесь используются измерения вектора кажущегося ускорения,которые осуществляются с помощью акселерометров. Системы, реализующие данный метод, принято называть инерциальными навигационными системами (ИНС).

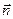
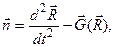
Линейные акселерометры – это измерительные приборы, которые реагируют на линейное ускорение своего основания (корпуса) по отношению к свободно падающему телу и используются для измерения этого, т. е. кажущегося ускорения основания, на котором они установлены.

(1)

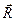
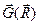
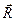
здесь — радиус-вектор, определяющий положение корпуса прибора относительно ц.м. Земли;

— удельная сила притяжения Земли в центре корпуса акселерометра и являющаяся функцией радиус-вектора .

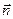
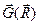
Уравнение (1) иногда называют основным уравнением инерциальной навигации, т.к. в его интегрировании и состоитсущность метода инерциальной навигации. Т.е. по измеренным составляющим вектора и априори известной зависимости путем двойного интегрирования при известных начальных условиях и заданной или вычисленной ориентации измерительных осей акселерометров относительно навигационных осей можно определять линейную скорость и координаты местоположения подвижного объекта.

Задачей ИНС является выработка кинематических параметров движения объекта: как навигационных (характеризующих поступательное движение ц.м. объекта в низкочастотной области спектра), так и динамических (характеризующих высокочастотное угловое и линейное движение с учетом рыскания, качки и орбитального движения некоторой точки корабля относительно его ц.м.).

Алгоритм идеальной работы автономных БИНС

В состав БИНС входят инерциальный измерительный модуль (ИИМ), содержащий чувствительные элементы – акселерометры и гироскопы, и вычислитель, реализующий алгоритмы работы БИНС. При этом акселерометры вырабатывают первичную навигационную информацию (производят первичные навигационные измерения). Гироскопы в БИНС — три датчика угловой скорости (ДУС) типа лазерного, волоконно-оптического или микромеханического гироскопа используются для определения (вычисления) угловой ориентации блока акселерометров относительно выбранной навигационной системы координат.

Вырабатываемыми кинематическими параметрами (выходная информация вычислителя) являются:

— углы курса, бортовой и килевой качки, определяющие ориентацию осей ИИМ БИНС относительно сопровождающего географического трехгранника ;

— восточная, северная и вертикальная составляющие линейной скорости объекта относительно Земли;

— широта, долгота и высота места объекта.

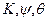
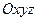
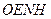
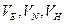
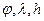
Первичными навигационными измерениями (исходной информацией для выработки выходных данных) ИИМ на ДУС являются:

— составляющие вектора кажущегося ускорения на оси ИИМ;

— составляющие вектора угловой скорости вращения трехгранника на свои оси.

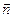
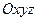
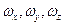
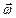
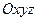
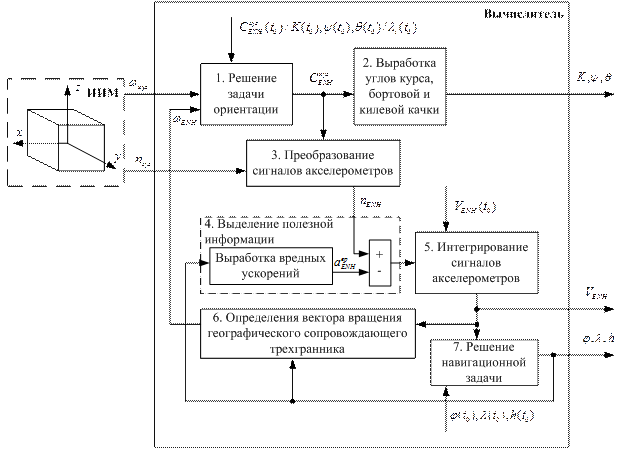
Рис. 1. Блок-схема алгоритма идеальной работы автономных БИНС

Блок-схема алгоритма идеальной работы автономных БИНС приведена на рис.1 и состоит из следующих блоков:

1. Решение задачи ориентации

Определение ориентации ИИМ БИНС, содержащего блок акселерометров, и подвижного объекта в целом относительно сопровождающего географического трехгранника с целью приведения сигналов акселерометров к осям навигационного сопровождающего трехгранника необходимой для последующего решения навигационной задачи. Ориентация объекта и блока акселерометров в частности задаётся матрицей направляющих косинусов, т.е. матрицей перехода от осей 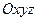связанных с объектом (рис. 2) к географическим осям (рис. 3). Обычно оси ИИМ совпадают со связанными с объектом.

Задача ориентации решается с использованием данных блока гироскопов. В БИНС с ИИМ на ДУС — это интегрирование кинематических уравнений вращательного движения объекта с целью вычисления матрицы ориентации

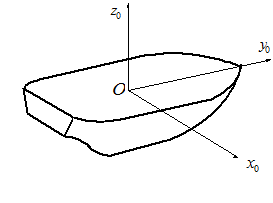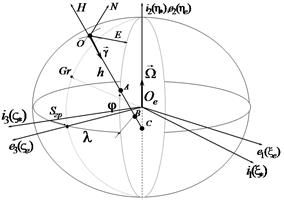Рис.2. Система координат 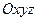, связанная с корпусом объекта	Рис.3. Географический сопровождающий трехгранник и инерциальная СК

Кинематические уравнениясвязывают вектор 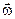угловой скорости вращения объекта с производными по времени от параметров ориентации. Вид кинематических уравнений определяется в зависимости от кинематических параметров, поэтому для углов Эйлера-Крылова, направляющих косинусов, и параметров Родрига-Гамильтона уравнения различны. Для решения кинематических уравнений, как и для любых других дифференциальных уравнений, должны быть известны начальные условия, для чего решается задача начальной выставки.

Для углов Эйлера-Крылова

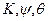
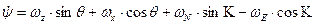
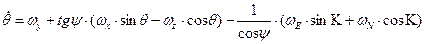
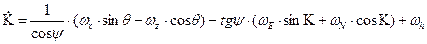
Когда преобразование задается тремя последовательными плоскими поворотами на углы курса, килевой и бортовой качки , то кинематические уравнения имеют следующий вид

,

, (2)

,

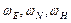
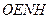
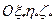
где – проекции на свои оси угловой скорости вращения географического сопровождающего трехгранника относительно инерциальной СК .

Матрица ориентации вычисляется следующим образом

. (3)

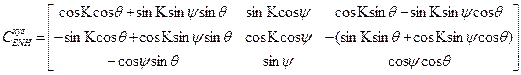
Для направляющих косинусов (уравнение Пуассона)

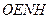
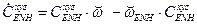
Если на борту подвижного объекта необходимо определять его ориентацию относительно системы координат, которая вращается в инерциальном пространстве, например, географического сопровождающего трехгранника , тогда необходимо воспользоваться обобщенным уравнением Пуассона

, (4)

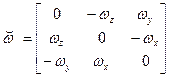
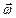
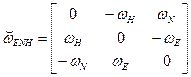
где — кососимметрическая матрица, соответствующая вектору ;

— кососимметрическая матрица, соответствующая вектору угловой скорости вращения географического сопровождающего трехгранника относительно инерциальной СК в проекции на свои оси.

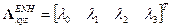
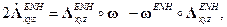
В кватернионной форме для кватерниона осуществляющий переход от географического сопровождающего трехгранника к связанному кинематические уравнения имеют вид

(5)

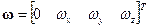
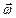
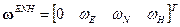
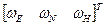
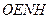
где – гиперкомплексное отражение вектора ;

– гиперкомплексное отражение вектора угловой скорости вращения географического сопровождающего трехгранника относительно инерциальной СК в проекции на свои оси.

Или в матричной форме:

. (6)

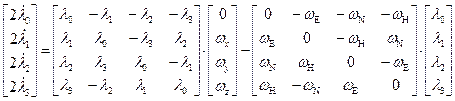
Матрица ориентации формируется по параметрам Родрига-Гамильтона следующим образом

. (7)

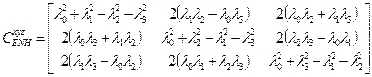
2. Выработка углов курса, бортовой и килевой качки

Если кинематические уравнения представлены в виде (4,5), то зная элементы матрицы ориентации можно вычислить выходные параметры ориентации, т.е. углы по следующим формулам:

, , , (8)

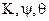
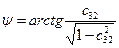
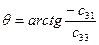
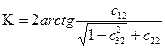
где 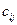— элементы матрицы ориентации .

Поскольку модули углов и меньше 90º, то приведенные выше выражения однозначно определяют значения углов килевой и бортовой качек. Внутри диапазона от 0 до 360º функция разрывов не имеет и однозначно определяет значение угла .

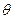
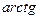
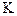
3. Преобразование сигналов акселерометров

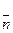
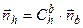
Используя решение задачи ориентации, значения вектора кажущегося ускорения, измеряемого блоком акселерометров в осях ИИМ, преобразуются к осям географического сопровождающего трехгранника следующим образом

. (9)

4. Выделение из сигналов акселерометров полезной информации

Так как задача навигации подвижного объекта решается вблизи поверхности Земли, то из сигналов акселерометров 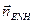, приведенных к осям географического сопровождающего трехгранника, необходимо исключить так называемые «вредные» ускорения, определяющие кориолисово и переносное ускорения ц.м. объекта или точнее точки расположения блока акселерометров на объекте, а также составляющие вектора ускорения силы тяжести.

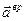
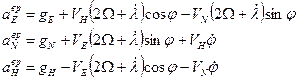
Значения «вредных» ускорений формируются в вычислителе БИНС по данным, вырабатываемым самой БИНС, и априорным данным о параметрах Земли: форме, размерах и угловой скорости вращения, по следующим формулам:

(10)

Для формирования модельных значений вектора необходимо располагать соответствующей моделью гравитационного поля Земли:

, (11)

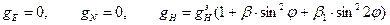
где м/с 2 , для параметров эллипсоида Красовского: b=0.0053171, b₁=0.0000071.

5. Интегрирование сигналов акселерометров,

Сигналы акселерометров «очищенных» от «вредных» ускорений интегрируются с привлечением начальных условий о составляющих вектора линейной скорости объекта в навигационных осях:

(12)

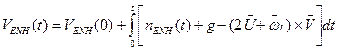
6. Вычисление текущих значений составляющих

вектора угловой скорости вращения географического сопровождающего трехгранника 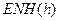по данным о составляющих вектора линейной скорости объекта в навигационных осях, радиусах кривизны нормальных сечений и широте места для формирования обратной связи в задачу ориентации.

Составляющие определяются соотношениями

, , , (13)

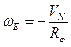
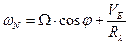
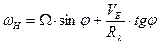
где 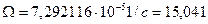°/ч — угловая скорость суточного вращения Земли.

Радиусы кривизны нормальных сечений:

(14)

м – параметры эллипсоида Красовского.

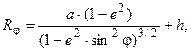
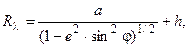
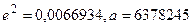
7. Решение навигационной задачи

Интегрирование составляющих вектора линейной скорости объекта в навигационных осях с привлечением начальных условий о координатах места объекта

(15)

.

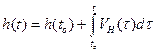
Распределение Пуассона: формулы, уравнения, модель, свойства

Распределение Пуассона: формулы, уравнения, модель, свойства — Наука

Содержание:

В распределение Пуассона Это дискретное распределение вероятностей, с помощью которого можно узнать вероятность того, что в пределах большого размера выборки и в течение определенного интервала произойдет событие, вероятность которого мала.

Часто вместо биномиального распределения можно использовать распределение Пуассона, если выполняются следующие условия: большая выборка и малая вероятность.

Симеон-Дени Пуассон (1781-1840) создал это распределение, носящее его имя, очень полезное, когда дело доходит до непредсказуемых событий. Пуассон опубликовал свои результаты в 1837 году — исследование вероятности появления ошибочных уголовных приговоров.

Позже другие исследователи адаптировали распределение в других областях, например, количество звезд, которые можно найти в определенном объеме пространства, или вероятность того, что солдат погибнет от удара лошади.

Формула и уравнения

Математическая форма распределения Пуассона следующая:

– μ (также иногда обозначается как λ) среднее значение или параметр распределения

— Число Эйлера: е = 2,71828

— Вероятность получения y = k равна P

– k количество успехов 0, 1,2,3 .

– п количество тестов или событий (размер выборки)

Дискретные случайные величины, как видно из их названия, зависят от случая и принимают только дискретные значения: 0, 1, 2, 3, 4…, k.

Среднее значение распределения определяется как:

Дисперсия σ, которая измеряет разброс данных, является еще одним важным параметром. Для распределения Пуассона это:

Пуассон определил, что при n → ∞ и p → 0 среднее μ — также называется ожидаемое значение— стремится к постоянной:

Важный: п — вероятность наступления события с учетом всего населения, а P (у) предсказание Пуассона на выборке.

Модель и свойства

Распределение Пуассона обладает следующими свойствами:

-Объем выборки большой: п → ∞.

— Рассматриваемые события или события не зависят друг от друга и происходят случайным образом.

-Вероятность п это определенное событие Y происходит в течение определенного периода времени очень мало: P → 0.

-Вероятность более одного события, произошедшего во временном интервале, равна 0.

-Среднее значение приближается к константе, определяемой: μ = n.p (n — размер выборки)

-Поскольку дисперсия σ равна μ, по мере того, как она принимает большие значения, изменчивость также становится больше.

-События должны быть равномерно распределены в используемом временном интервале.

-Множество возможных значений события Y составляет: 0,1,2,3,4….

-Сумма я переменные, которые следуют распределению Пуассона, также являются другой переменной Пуассона. Его среднее значение — это сумма средних значений этих переменных.

Отличия от биномиального распределения

Распределение Пуассона отличается от биномиального распределения следующими важными способами:

-Биномиальное распределение зависит как от размера выборки n, так и от вероятности п, но на распределение Пуассона влияет только среднее μ.

-В биномиальном распределении возможные значения случайной величины Y они равны 0,1,2,…, N, однако в распределении Пуассона для этих значений нет верхнего предела.

Примеры

Первоначально Пуассон применил свой знаменитый дистрибутив к судебным делам, но на промышленном уровне одним из первых его применений было пивоварение. В этом процессе для брожения используются дрожжевые культуры.

Дрожжи состоят из живых клеток, популяция которых меняется во времени. При изготовлении пива необходимо добавлять необходимое количество, поэтому необходимо знать количество ячеек в единице объема.

Во время Второй мировой войны распределение Пуассона использовалось, чтобы выяснить, действительно ли немцы целятся в Лондон из Кале или стреляют наугад. Для союзников было важно определить, насколько хорошие технологии были доступны нацистам.

Практическое применение

Приложения распределения Пуассона всегда относятся к счетам во времени или счетам в пространстве. А поскольку вероятность возникновения невелика, его еще называют «законом редких событий».

Вот список событий, которые попадают в одну из этих категорий:

-Регистрация частиц в радиоактивном распаде, который, как и рост дрожжевых клеток, является экспоненциальной функцией.

-Количество посещений определенного сайта.

-Прибытие людей к очереди для оплаты или присутствия (теория очереди).

-Количество автомобилей, которые проезжают определенную точку дороги за заданный промежуток времени.

— Мутации, произошедшие в определенной цепи ДНК после облучения.

-Количество метеоритов диаметром более 1 м, выпавших за год.

-Дефекты на квадратный метр ткани.

-Количество кровяных телец в 1 кубическом сантиметре.

-Звонков поминутно на АТС.

-Шоколадные чипсы присутствуют в 1 кг теста для торта.

-Количество деревьев, зараженных определенным паразитом, на 1 га леса.

Обратите внимание, что эти случайные переменные представляют количество раз, когда событие происходит в течение фиксированного периода времени (звонков за минуту на телефонную станцию) или заданный регион пространства (дефекты ткани на квадратный метр).

Эти события, как уже было установлено, не зависят от времени, прошедшего с момента последнего события.

Аппроксимация биномиального распределения распределением Пуассона

Распределение Пуассона является хорошим приближением к биномиальному распределению, если:

-Размер выборки большой: п ≥ 100

-Вероятность рмаленький: р ≤ 0,1

– μ находится в следующем порядке: np ≤ 10

В таких случаях распределение Пуассона является отличным инструментом, поскольку в этих случаях может быть трудно применить биномиальное распределение.

Решенные упражнения

Упражнение 1

Сейсмологическое исследование показало, что за последние 100 лет во всем мире произошло 93 сильных землетрясения силой не менее 6,0 баллов по логарифмической шкале Рихтера. Предположим, что распределение Пуассона является подходящей моделью в этом случае. Найти:

а) Среднее количество сильных землетрясений в год.

б) да P (у) это вероятность появления Y землетрясения в течение случайно выбранного года, найдите следующие вероятности:

c) Истинные результаты исследования следующие:

– 47 лет (0 землетрясений)

— 31 год (1 землетрясение)

— 13 лет (2 землетрясения)

— 5 лет (3 землетрясения)

— 2 года (4 землетрясения)

— 0 лет (5 землетрясений)

— 1 год (6 землетрясений)

— 1 год (7 землетрясений)

Как эти результаты соотносятся с результатами, полученными в части b? Подходит ли распределение Пуассона для моделирования этих событий?

Решение для)

а) Землетрясения — это события, вероятность которых п он небольшой, и мы рассматриваем ограниченный период времени в один год. Среднее количество землетрясений:

μ = 93/100 землетрясений / год = 0,93 землетрясений в год.

Решение б)

б) Для расчета требуемых вероятностей значения подставляются в формулу, приведенную в начале:

Это намного меньше, чем P (2).

Результаты перечислены ниже:

P (0) = 0,395, P (1) = 0,367, P (2) = 0,171, P (3) = 0,0529, P (4) = 0,0123, P (5) = 0,00229, P (6) = 0,000355, P (7) = 0,0000471.

Например, мы могли бы сказать, что существует вероятность 39,5%, что в данном году не произойдет сильного землетрясения. Или что в этом году произошло 5,29% из 3 крупных землетрясений.

Решение c)

в) Частоты анализируются, умножая на n = 100 лет:

39,5; 36,7; 17,1; 5,29; 1,23; 0,229; 0,0355 и 0,00471.

— Частота 39,5 указывает на то, что за 39,5 лет из 100 происходит 0 сильных землетрясений, мы можем сказать, что это довольно близко к фактическому результату за 47 лет без каких-либо крупных землетрясений.

Давайте сравним другой результат Пуассона с реальными результатами:

— Полученное значение 36,7 означает, что за 37 лет произошло 1 сильное землетрясение. Фактический результат состоит в том, что за 31 год произошло 1 сильное землетрясение, что хорошо соответствует модели.

— Ожидается 17,1 года с 2 сильными землетрясениями, и известно, что за 13 лет, что является близким значением, действительно было 2 сильных землетрясения.

Поэтому для этого случая приемлема модель Пуассона.

Упражнение 2.

По оценке одной компании, количество компонентов, которые выходят из строя до достижения 100 часов работы, следует распределению Пуассона. Если за это время среднее количество отказов равно 8, найдите следующие вероятности:

а) Что компонент выходит из строя через 25 часов.

б) Отказ менее двух компонентов за 50 часов.

c) По крайней мере, три компонента выходят из строя за 125 часов.

Решение для)

а) Известно, что в среднем за 100 часов отказов 8, поэтому за 25 часов ожидается четверть отказов, то есть 2 отказа. Это будет параметр μ.

Требуется вероятность отказа 1 компонента, случайная величина — «компоненты, которые выходят из строя до 25 часов», а ее значение — y = 1. Подставив в функцию вероятности:

Однако вопрос в вероятности того, что они выйдут из строя. менее двух компонентов за 50 часов не точно 2 компонента выйдут из строя за 50 часов, поэтому необходимо добавить вероятности, что:

-Ошибка только 1

P (отказ менее 2 компонентов) = P (0) + P (1)

P (отказ менее 2 компонентов) = 0,0183 + 0,0732 = 0.0915

в) что они терпят неудачу по крайней мере 3 компонента за 125 часов означает, что 3, 4, 5 или более могут выйти из строя за это время.

Вероятность того, что это произойдет по крайней мере одно из нескольких событий равно 1 минус вероятность того, что ни одно из событий не произойдет.

— Желаемое событие — отказ 3 или более компонентов за 125 часов

-Неисправность означает отказ менее 3 компонентов, вероятность которого составляет: П (0) + П (1) + П (2)

Параметр μ распределения в этом случае равен:

μ = 8 + 2 = 10 отказов за 125 часов.

P (3 или более компонентов выходят из строя) = 1- P (0) — P (1) — P (2) =

Ссылки

1. MathWorks. Распределение Пуассона. Получено с: es.mathworks.com
2. Менденхолл, В. 1981. Статистика для управления и экономики. 3-й. издание. Grupo Редакционное Ибероамерика.
3. Stat Trek. Изучите статистику. Распределение Пуассона. Получено с: stattrek.com,
4. Триола, м. 2012. Элементарная статистика. 11-е. Под ред. Пирсона Образование.
5. Википедия. Распределение Пуассона. Получено с: en.wikipedia.org

Что такое детрит? (В биологии, геологии и медицине)

Уравнение Пуассона и распределение Больцмана (часть 1)

В продолжение предыдущей статьи «Есть ли плазма в космосе?» я хотел бы в познавательных целях рассказать об уравнениях, которые применялись при выводе уравнения Дебая-Хюккеля. Это уравнение Пуассона и распределение Больцмана.

Мы выяснили, что плазма квазинейтральна в равновесном состоянии и что под действием электрического поля от движущихся зарядов, заряженные частицы смещаются на дебаевскую длину и поле в пределах этой длины затухает. В электростатике взаимодействие заряженных частиц описывается кулоновским уравнением:

где – величины взаимодействующих точечных зарядов, – квадрат расстояния между зарядами. Коэффициент k является константой. Если мы используем систему в электростатических единицах СГС, обозначаемых СГСЭq, то k = 1. Если используется система СИ, то , где – диэлектрическая проницаемость среды, в которой расположены заряды, – электрическая постоянная, равная 8,86 ∙ .

В физике непосредственно силой не пользуются, а вводят понятие электростатического поля распределённых зарядов и измеряют поле величиной напряженности электрического поля. Для этого в каждую точку поля мысленно помещают единичный пробный заряд и измеряют силу, с которой поле зарядов действует на пробный заряд:

Отсюда, если подставить в это уравнение силу Кулона, то получим:

Но и этим физики не ограничиваются, для того чтобы описать полноценно электрическое поле. Рассмотрим единичный заряд, помещённый в электростатическое поле. Поле выполняет работу по перемещению этого заряда на элементарное расстояние ds из точки P1 в точку P2:

Величину называют разностью потенциалов или напряжением. Напряжение измеряется в Вольтах. Знак минус говорит нам о том, что само поле выполняет работу для переноса единицы положительного заряда. Силы, перемещающие заряды являются консервативными, так как работа по замкнутому пути равна всегда нулю, независимо от того, по какому пути перемещается заряд.

Отсюда следует глубокий смысл разности потенциалов. Если зафиксировать точку Р1 и перемещать заряд в переменную точку Р2, то работа зависит только от положения второй точки Р2. Таким образом мы можем ввести понятие потенциала. Потенциал – это силовая функция, показывающая какую необходимо выполнить работу полю, чтобы переместить заряд из бесконечности в данную точку P2, где условно принимают потенциал в бесконечности равным нулю.

Чтобы понять уравнение Пуассона, необходимо разбираться в «особой» векторной математике. Я вкратце расскажу про такие понятия как градиент поля и дивергенции (подразумевается, что читатель знаком с математическим анализом)
Пусть f(x,y,z) является некоторой непрерывной дифференцируемой функцией координат. Зная её частные производные в каждой точке пространства можно построить вектор, компоненты которого x, y, z равны соответствующим частным производным:

где – единичные векторы соответствующих осей x, y, z. Значок читается «набла» и является дифференциальным оператором

Этот оператор ввёл в математику Гамильтон. С набла можно выполнять обычные математические операции, такие как обычное произведение, скалярное произведение, векторное произведение и так далее.

Теперь вернёмся к электростатическому полю E. С одной стороны изменение потенциала при переходе из одной точки в другую имеет следующий вид:

С другой стороны, согласно формуле (*)

Применяя только что введённое понятие градиент, эта формула преобразуется в:

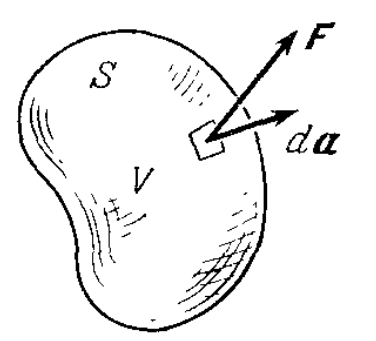
Теперь разберёмся с таким понятием, как дивергенция поля. Рассмотрим конечный замкнутый объем V произвольной формы (см. рис. ниже). Обозначим площадь этой поверхности S. Полный поток вектора F, выходящего из этого объема по определению равно

, где da является бесконечно малым вектором, величина которого равна площади малого элемента поверхности S, а направление совпадает с наружной нормалью к этому элементу.
Возьмём этот поток вектора F поделим на объём и найдём предел при стремящейся к нулю, т.е. будем стягивать объём в бесконечно малую точку.

Мы подошли к понятию дивергенции. Обозначается дивергенция символом div и является отношением потока вектора F к объёму V, при V стремящейся к нулю.

Прежде чем показать, как получается уравнение Пуассона, важно знать закон Гаусса и теорему Гаусса. Представим себе сферу, внутри которой находится заряд q. Заряд создаёт вокруг себя электрическое поле напряжённости E. Возьмём поток вектора E

где S площадь нашей сферы равная . Следовательно

Это и есть закон Гаусса, утверждающий, что поток электрического поля E через любую замкнутую поверхность равен произведению на полный заряд, охватываемый поверхностью:

где – плотность объёмного заряда, т.е. величина электрического заряда в единице объёма, и – элементарный объём, выделенный внутри нашего замкнутого объёма.

Теорема Гаусса (полное название теорема Гаусса-Остроградского) чисто математическая теорема о дивергенции. Перепишем полный поток вектора F следующим образом:

В пределе, когда N → ∞, →0 величина в скобках становится дивергенцией и сумма переходит в объёмный интеграл:

Это и есть теорема Гаусса, и является поистине самой важной формулой полевой теории. Применим эту теорему к электростатическому полю. С одной стороны, согласно закону Гаусса

А с другой стороны, согласно теореме Гаусса (только не путайте теорему с законом Гаусса):

Комбинируя два последних уравнения, получим:

Вспомним формулу (**) и подставим сюда вместо E потенциал поля

Дивергенция градиента это новый оператор, который в математике называют оператор Лапласа, или сокращённо лапласиан. Лапласиан обозначается значком набла следующим образом и равен

Перепишем предыдущую формулу в форме лапласиана:

Наконец мы получили уравнение Пуассона. В первой статье это уравнение было немного в другой форме, с учётом диэлектрической проницаемости среды. Вспомните силу Кулона в системе СИ, там константа . Соответственно в законе Гаусса будет не , а коэффициент . Таким образом получаем уравнение Пуассона в форме представленной в предыдущей статье

Таким образом по сути уравнение Пуассона – это закон Кулона (а точнее закон Гаусса) переписанный в другой форме, в обозначениях векторного дифференциального анализа.

В следующей статье мы разберём важное распределение из математической статистики — распределение Больцмана.