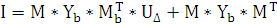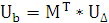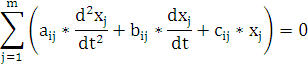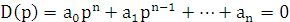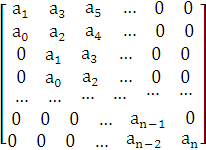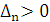Матричная форма уравнений состояния ЭЭС
Матричное уравнение состояния ЭЭС — система уравнений, описывающая режим работы ЭЭС.
Виды матричных уравнений состояния:
1. Обобщенное уравнение состояния.
2. Уравнение узловых напряжений.
3. Уравнение контурных токов.
Обобщенное уравнение состояния получается за счет объединения уравнений состояния, составленных по 1-му и 2-му законам Кирхгофа.

Матричная форма представления уравнения узловых напряжений
Ток ветвей из 1-ого закона Ома
Из 1-ого закона Кирхгофа

Обозначим 
Физический смысл матрицы узловых проводимостей следующий: на главной диагонали расположены элементы 

Этапы расчета по методу узловых напряжений.
1. Определяются значения узловых напряжений
2. Определяются падения напряжений в ветвях
3. Определяются токи ветвей из закона Ома
4. Рассчитываются остальные параметры режима.
Матричная форма представления уравнений контурных токов
Ток ветвей из 2-ого закона Кирхгофа
Обозначим 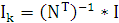

Физический смысл матрицы контурных токов следующий: на главной диагонали расположены элементы 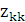

При наличии задающих токов в схеме равнения контурных токов имеют вид

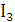
Для получения 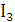

Матрица 
Матрица 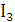

Рассчитать установившийся режим работы СЭС. Исходные данные приведены в таблице 3.1.
| Вариант | Рисунок | Параметры ЛЭП, погонное сопротивление, Ом/км |
| 1,2,3 | 4,5 | 6,7 |
| 0,075+j0,420 | 0,098+j0,429 | 0,121+j0,435 |
| 0,121+j0,435 | 0,075+j0,420 | 0,098+j0,429 |
| 0,098+j0,429 | 0,121+j0,435 | 0,075+j0,420 |
| 0,075+j0,420 | 0,098+j0,429 | 0,121+j0,435 |
| 0,121+j0,435 | 0,075+j0,420 | 0,098+j0,429 |
| 0,098+j0,429 | 0,121+j0,435 | 0,075+j0,420 |
| 0,075+j0,420 | 0,098+j0,429 | 0,121+j0,435 |
| 0,121+j0,435 | 0,075+j0,420 | 0,098+j0,429 |
| 0,098+j0,429 | 0,121+j0,435 | 0,075+j0,420 |
| 0,075+j0,420 | 0,098+j0,429 | 0,121+j0,435 |
Продолжение таблицы 3.1
| Вариант | Параметры ЛЭП, длина, км | Задающие мощности нагрузок узлов, МВА | ||
| 70+j30 | 75+j40 | 110+j30 | 100+j40 | 80+j50 |
| 80+j50 | 100+j40 | 75+j40 | 75+j40 | 120+j50 |
| 120+j50 | 80+j50 | 75+j35 | 80+j50 | 100+j40 |
| 100+j40 | 70+j30 | 100+j40 | 110+j30 | 75+j40 |
| 75+j40 | 120+j50 | 80+j50 | 75+j40 | 75+j35 |
| 110+j30 | 75+j35 | 70+j30 | 100+j40 | 80+j50 |
| 80+j50 | 75+j40 | 120+j50 | 80+j50 | 110+j30 |
| 75+j35 | 100+j40 | 75+j40 | 70+j30 | 120+j50 |
| 120+j50 | 80+j50 | 100+j40 | 120+j50 | 100+j40 |
| 75+j40 | 110+j30 | 80+j50 | 75+j35 | 70+j30 |
Варианты исходных схем
Расчётная работа 4.
Расчет устойчивости СЭС
— изучить методы определения устойчивости СЭС;
— изучить критерии устойчивости методов;
Основные теоретические положения:
Методы исследования статической устойчивости электроэнергетических систем.
Постановка задачи расчетов:
Задача исследования устойчивости ЭЭС требует наличия методов, которые давали бы возможность по доступным, легко полученным признакам, устанавливать устойчивость системы.
Критерий устойчивости- необходимое и/ или достаточное условие (группа условий), при выполнении которых система является устойчивой.
Основной критерий устойчивости состояния системы
Характеристическое уравнение имеет вид
Равенство нулю характеристического уравнения возможно, только если все его корни имеют отрицательные вещественные части.
Для того, чтобы состояние равновесия было устойчивым, необходимо и достаточно, чтобы все корни характеристического уравнения лежали в левой комплексной полуплоскости.
Характеристическое уравнение, как правило, имеет несколько действительных и несколько комплексно-сопряженных корней. При простых корнях общее решение системы имеет вид


Алгебраический критерий устойчивости.
Содержит группу условий — неравенств, при соблюдении которых система устойчива.
Для проведения алгебраического анализа необходимы коэффициенты характеристического уравнения.
1. Если все коэффициенты 
2. Если при изменении параметров системы хотя бы один из коэффициентов меняет знак, система неустойчива.
3. Необходимые условия устойчивости представляют собой различные соотношения.
Устанавливает соотношения в форме неравенств, соблюдение которых является необходимым и достаточным условием устойчивости системы.
Все коэффициенты с индексом i n обозначаются нулями.
Для соблюдения устойчивости требуется, чтоб все n диагональных миноров матрицы Гурвица были положительны.
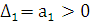

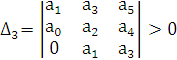
Критерий Гурвица используется для определения устойчивости систем 3-4-го порядков.
Используется для систем порядка выше 4, когда параметры заданы числами.
Из коэффициентов характеристического уравнения составляется таблица Рауса с количеством строк n+1 .
Элементы 1-й строки- коэффициенты с четными индексами.
Элементы 2-й строки- коэффициенты с нечетными индексами.
Элементы следующих строк находятся по формуле

Необходимое и достаточное условие устойчивости:
Все коэффициенты первого столбца должны быть положительны


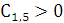
Число перемен знаков в 1-м столбце таблицы Рауса равно числу корней характеристического уравнения.
  |   |   |   | |
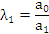 | 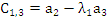 | 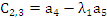 | 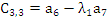 |  |
 |  | 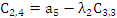 |  |  |
 |  | 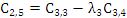 | 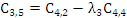 |  |
Если числа в 1-м столбце отличны от нуля, таблица называется регулярной. В регулярном случае характеристическое уравнение не имеет чисто мнимых корней.
Если в 1-м столбце есть нулевой элемент, таблица называется нерегулярной. В этом случае для построения таблицы строку, в которой элементы 
Разность между числом нулей и числом полюсов функции F(p) внутри контура С равен числу оборотов, которое делает вектор в плоскости W(jω), идущий из O в F(p), когда точка p описывает контур С.
Для отсутствия корней с положительной действительной частью характеристического уравнения ( т.е. для обеспечении устойчивости), необходимо и достаточно, чтобы при прохождении точкой p мнимой оси в положительном направлении приращение аргумента D(p) было равно n.П.
Характеристическое уравнение представим в виде
Для определения устойчивости по Михайлову необходимо определить приращение аргумента 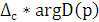


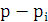
Вектор 
Характеристический вектор, изображенный в декартовых координатах U и V при изменении 
Система устойчива, если 
Система неустойчива, если 
Для обеспечения устойчивости необходимо и достаточно:
1.
2.
3. Все корни уравнений 
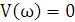
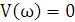
Для анализа устойчивости системы, ряд звеньев которой задан лишь амплитудно-фазовыми характеристиками, применяют критерий Найквиста.
Критерий Найквиста основан на применении принципа аргумента к вектору — годографу комплексного коэффициента усиления разомкнутой системы.
Он позволяет по АФХ разомкнутой системы определить устойчивость соответствующей замкнутой системы.
Необходимое и достаточное условие устойчивости замкнутой системы:
1. Для устойчивой разомкнутой системы
2. Для неустойчивой разомкнутой системы
Возможная формула АФХ разомкнутой системы определяются рядом условий:
1. Если многочлен Q(p)и R(p) имеют положительные свободные члены 
2. Если многочлен Q(p)имеет нулевой корень, т.е. разомкнутся система находится на границе апериодической устойчивости (нейтральна), 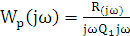
3. Если Q(p)имеет пару чисто мнимых корней . т.е. разомкнутая система находится на границе периодической устойчивости(нейтральна ) 
4. Если степень R(p) меньше, чем Q(p) , 
Если степени R(p)и Q(p)равны, 
Вектор 1+ 





Геометрическая формулировка критерия Найквиста:
Для устойчивости замкнутой системы необходимо и достаточно, чтобы:
1. АФХ устойчивой или нейтральной разомкнутой системы не охватывала точкуС(-1;0)
2. АФХ неустойчивой разомкнутой системы охватывала точку С(-1;0) 
Если многочлен Q(jω) имеет высокую степень, то для построения АФХ разомкнутой системы требуется большие вычисления. В этом случае удобнее использовать инверсную амплитудно-фазовую характеристику

Критерии Найквиста для ИАФХ:
Для устойчивости замкнутой системы необходимо и достаточно, чтобы ИАФХ устойчивой разомкнутой системы охватывала точку С (-1;0)
D‑разбиение по двум параметрам.
Будем рассматривать наиболее распространенный случай, когда два параметра входят в характеристический многочлен линейно (т. е. ни в одном из коэффициентов многочлена нет ни произведения, ни высших степеней П). Характеристическое уравнение системы
Найдем значения П1 и П2, при которых характеристическое уравнение имеет пару чисто мнимых корней р1,2 =± jωi.
Уравнение распадается на два:
Решим систему с помощью правила Крамера:


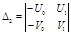
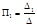

Кривые П1(ω), П2(ω) – четные функции, т.е. П(–ω) = П(ω). Определители Δ(ω), Δ1(ω), Δ2(ω) – нечетные функции. При изменении ω от –∞ до 0 получим кривую D‑разбиения на плоскости параметров П1 и П2. При изменении ω от 0 до +∞ получим ту же кривую, т.к. функции П(ω) – четные.
При изменении ω главный определитель Δ может менять знак. Прохождение значения Δ через нуль соответствует двум случаям:
1) при Δ = 0 значения Δ1 и Δ2 конечны и не равны нулю. Тогда П1 и П2 обращаются в бесконечность.
2) при Δ = 0 значение Δ1= Δ2 = 0. Тогда П1 и П2 становятся неопределенными. Равенство нулю определителей при фиксированном значении ωi означает, что все коэффициенты двух уравнений пропорциональны:
Тогда вместо двух уравнений можно записать одно:
Это соотношение определяет в плоскости П2, П1 для некоторого фиксированного значения ω = ωi положение линии, называемой особой прямой. Чтобы найти особые прямые, надо определить все значения ωi, при которых одновременно Δ = Δ1= Δ2 = 0.
Для получения особых прямых нужно:
1) Приравнять а0 = 0, если оно зависит от П1, П2, и получить уравнение особой прямой, соответствующей ω = ∞;
2) Приравнять ап = 0, если оно зависит от П1, П2, и получить уравнение особой прямой, соответствующей ω = 0;
3) Найти все отличные от нуля значения ω, при которых Δ = Δ1= Δ2 = 0. Подставив эти значения ω в уравнение, получим уравнения соответствующих особых прямых.
Штриховка границ D-разбиения.

Пусть изображающая точка М перемещается по плоскости П2, П1. До тех пор пока она перемещается внутри области D(m), и не попадает на кривую D-разбиения, число корней т в правой полуплоскости остается постоянным. Как только точка М попадает на кривую D-разбиения, на мнимую ось плоскости р выйдет пара корне й. При пересечении кривой D-разбиения эта пара корней перейдет из одной полуплоскости в другую. Чтобы выяснить направление перехода корней (из левой полуплоскости корней в правую или наоборот), применяется правило штриховки.
Сравним движение по мнимой оси плоскости корней с направлением движения по кривой D‑разбиения. Если в плоскости корней перемещаться по мнимой оси из – ∞ в + ∞, то область, где должны располагаться корни для того, чтобы система была устойчива, будет всегда слева. Заштрихуем слева мнимую ось jω. Перемещаясь вдоль границы D-разбиения из точки, соответствующей ω = –∞, к точке, соответствующей ω = +∞, заштрихуем кривую также слева в том случае, если Δ > 0. Изменение знака определителя меняет направление штриховки.
Правило штриховки:при обходе в сторону возрастающих ω (от –∞ до +∞) кривая D‑разбиения штрихуется слева, если главный определитель Δ > 0, и справа, если Δ
Обобщенное уравнение состояния в матричной форме
Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.
Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где 
 . . | (1) |
Однако, для дальнейших выкладок будет удобнее представить ток 
 . . | (2) |
Подставив (2) в (1), получим:
 . . | (3) |
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства
 , , | (4) |
где Z – диагональная квадратная (размерностью матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому
 , , | (5) |
 , , | (6) |
то есть получили новую запись в матричной форме второго закона Кирхгофа.
Метод контурных токов в матричной форме
В соответствии с введенным ранее понятием матрицы главных контуров В , записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам.
Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c = n — m +1 . Выражение (6) запишем следующим образом:
 . . | (7) |
В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j –го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока j –й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения
 , , | (8) |
где 

С учетом (8) соотношение (7) можно записать, как:
 | (9) |
Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить
 , , | (10) |
 . . | (11) |
то получим матричную форму записи уравнений, составленных по методу контурных токов:
 , , | (12) |
где 

В развернутой форме (12) можно записать, как:
 , , | (13) |
то есть получили известный из метода контурных токов результат.
Рассмотрим пример составления контурных уравнений.
Пусть имеем схему по рис. 2. Данная схема имеет четыре узла ( m =4) и шесть обобщенных ветвей ( n =6). Число независимых контуров, равное числу ветвей связи,
Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.
Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:
B
Диагональная матрица сопротивлений ветвей
Z
Матрица контурных сопротивлений
Zk=BZB T

Матрицы ЭДС и токов источников
 |  |
 |  |
Тогда матрица контурных ЭДС

Матрица контурных токов
 |  . . |
Таким образом, окончательно получаем:

где 








Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.
Метод узловых потенциалов в матричной форме
На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:
 , , | (14) |
где 

Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа, согласно которому
 , , | (15) |
 .. .. | (16) |
Выражение (16) перепишем, как:
 . . | (17) |
Принимая потенциал узла, для которого отсутствует строка в матрице А , равным нулю, определим напряжения на зажимах ветвей:
 . . | (18) |
Тогда получаем матричное уравнение вида:
 . . | (19) |
Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить
 | (20) |
 , , | (21) |
то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:
 | (22) |
где 

В развернутом виде соотношение (22) можно записать, как:
 | (23) |
то есть получили известный из метода узловых потенциалов результат.
Рассмотрим составление узловых уравнений на примере схемы по рис. 4.
Данная схема имеет 3 узла ( m =3) и 5 ветвей ( n =5) . Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.
А
Диагональная матрица проводимостей ветвей:
Y
где 
Матрица узловых проводимостей

Матрицы токов и ЭДС источников
 |  |
 |  |
Следовательно, матрица узловых токов будет иметь вид:
Таким образом, окончательно получаем:

где 




Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В чем заключаются преимущества использования матричных методов расчета цепей?
- Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.
- Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
- Составить узловые уравнения для цепи на рис. 2.
Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано ветвями 3 и 4 (см. рис. 5).
№74 Расчет переходных процессов методом переменных состояния.
Уравнениями состояния электрической цепи называют любую систему дифференциальных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.
В более узком смысле в математике уравнениями состояния называют систему дифференциальных уравнений 1-го порядка, разрешенных относительно производных (форма Коши). Система уравнений состояния в обобщенной форме имеет вид:
Та же система уравнений в матричной форме:
или в обобщённой матричной форме:
Система уравнений состояния формы Коши решается методом численного интегрирования (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стандартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по следующему алгоритму (метод Эйлера) для к-го шага:
Значения производных на к-ом шаге:
Значения переменных на к-ом шаге:
Для определения значений переменных и их производных на 1-м шаге ин¬тегрирова¬ния используются их значения на момент t=0, т.е. их начальные условия x1(0), x2(0). xn(0).
Уравнения состояния формы Коши для заданной схемы могут быть получены из системы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются »лишние» переменные, имеющие зависимые начальные условия, и оставляют переменные iL(t) и uC(t), которые не изменяются скачком и имеют независи-мые начальные условия iL(0) и uC(0); б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.
В случае сложных схем уравнения состояния формы Коши могут быть составлены топологическими методами с использованием матриц соединений [A] и [B].
Последовательность расчета переходного процесса методом переменных состояния выглядит так:
1. Производится расчет схемы в установившемся режиме до коммутации и определяются независимые начальные условия iL(0) и uC(0).
2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.
3. Методом исключения »лишних» переменных система уравнений Кирхгофа преобразуется в систему уравнений Коши, составляются матрицы коэффициентов.
4. Выбирается расчетное время (продолжительность переходного процесса) и число шагов интегрирования N.
5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы x=f(t)или в виде таблицы координат функций для заданных моментов времени.
Пример. Для схемы рис. 74.1 с заданными параметрами элементов (e(t)=Emsin(ωt+ψE), R, R1, R2, R3, L1, L2, C) выполнить расчет переходного процесса и определить функцию uab(t).
1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия i1(0), i2(0), uC(0).
2. Составляется система дифференциальных уравнений по законам Кирхгофа:
3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.
Для этой цели из (1) выражаем
и делаем подстановку в (1) и (2), а из (4) делаем подстановку в (1). Тогда получим:
Подсчитаем значения отднльных коэфициэнтов:
Составляем матрицы коэффициентов:
В качества исследуемого промежутка времени выбираем период переменного тока
Число шагов интегрирования принимаем N = 1000,
Вводим исходные данные в ЭВМ и выполняем рассчет.
В качестве выходной функции принимаем:
Для выходной функции Uab(T) строим графическую диаграмму в интервале периода Т.
http://toehelp.ru/theory/toe/lecture06/lecture06.html
http://toehelp.com.ua/lectures/074.html