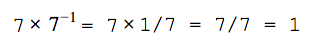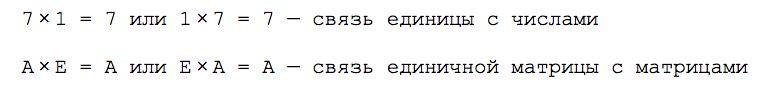Обратная матрица простейшие матричные уравнения ранг матрицы

Обратная матрица простейшие матричные уравнения ранг матрицы

4.1 ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ

Квадратная матрица А порядка n называется невырожденной (или неособенной), если det A ≠ 0. В противном случае матрица А – вырожденная (или особенная). Матрица A является обратной для квадратной невырожденной матрицы А, если A A AA E , где E ‑ единичная матрица порядка n :

.

Теорема 4.1. (необходимое и достаточное условие существования обратной матрицы). Обратная матрица A существует тогда и только тогда, когда исходная матрица А невырожденная .

Доказательство . Необходимость. Пусть матрица А имеет обратную A , т. е. A A AA E . По свойству 10 определителей имеем D ( A A ) = D ( A ) D ( А ) D ( E ) = 1 и, следовательно, D ( А ) 0.

Достаточность . Пусть D ( А ) 0. Рассмотрим квадратную матрицу n -го порядка , называемую присоединенной . Ее элементами служат алгебраические дополнения элементов матрицы , транспонированной к матрице А:

.

Легко показать, что

.

Отсюда следует, что если в качестве обратной матрицы взять матрицу A , то произведения A A и AA равны единичной матрице E n -го порядка: A A AA E .

Рангом матрицы А (обозначается rang А или r ( A )) является наибольший порядок порожденных ею миноров (определителей), отличных от нуля. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется ее базисным минором. Строки и столбцы, участвующие в образовании базисного минора, также будут базисными. Матрица может иметь несколько базисных миноров, однако все их порядки одинаковы и равны рангу матрицы.

Ранг матрицы не изменится, если:

1) строки и столбцы матрицы поменять местами;

2) переставить местами два любых ее столбца (строки);

3) удалить из нее столбец (строку), все элементы которого равны нулю;

4) удалить из нее столбец (строку), являющийся линейной комбинацией остальных ее столбцов (строк);

5) умножить ее произвольный столбец (строку) на любое отличное от нуля число;

6) к любому ее столбцу (строке) прибавить произвольную линейную комбинацию остальных столбцов (строк) этой матрицы.

Преобразования 2) ‑ 6) называются элементарными. Две матрицы являются эквивалентными, если одна получается из другой с помощью элементарных преобразований и обозначается как А

Для рангов матриц справедливы следующие соотношения:

1) r (A + В ) r(A) + r(B),

3) r (A В ) min<r(A); r(B)>,

5) r ( A В ) = r ( A ), если В – квадратная матрица и D ( В ) 0,

6) r ( A В ) r ( A ) + r (В) – n , где n – число столбцов матрицы А или строк матрицы В.

Что такое обратная матрица

Сложная тема из линейной алгебры.

Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко:

Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.

С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.

Читать ли эту статью?

❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной.

✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс.

Обратное — это как?

В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:

Обратные числа при умножении друг на друга всегда дают единицу:

Обратная матрица

В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.

Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:

Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.

Пример квадратной единичной матрицы размером 5×5. Единичная матрица может быть любого размера — состоять из любого количества строк и столбцов

Как рассчитать обратную матрицу

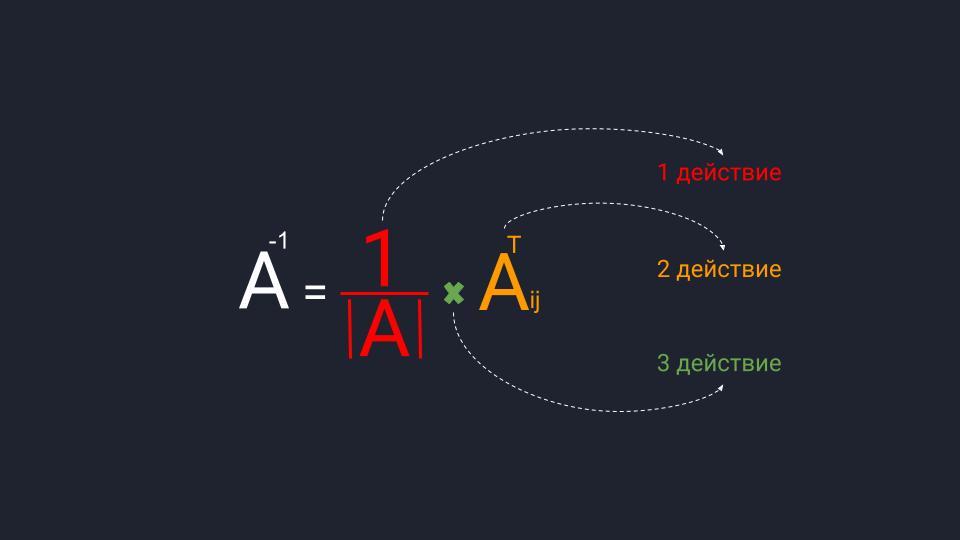
Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:

1. Разделить единицу на матричный определитель.
2. Найти транспонированную матрицу алгебраических дополнений.
3. Перемножить полученные значения.

Далее мы по порядку во всём разберёмся.

Формула расчёта обратной матрицы: |A| — матричный определитель; Aᵀᵢⱼ — матрица алгебраических дополнений

Определитель — это особое число, которое «определяет» свойства матрицы.

Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3.

Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.

Формула для расчёта определителя второго порядка

Пример расчёта определителя второго порядка

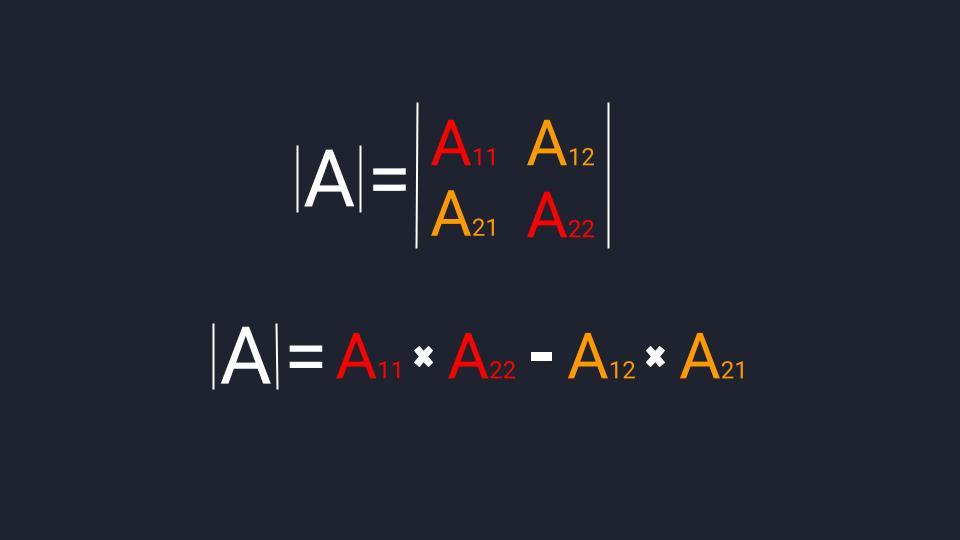
Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям.

Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.

Считаем определитель третьего порядка: 1-й этап — главная диагональ

Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.

Считаем определитель третьего порядка: 2-й этап — первый треугольник

Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.

Считаем определитель третьего порядка: 3-й этап — второй треугольник

Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.

Считаем определитель третьего порядка: 4-й этап — вторая диагональ

Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.

Считаем определитель третьего порядка: 5-й этап — третий треугольник

Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.

Считаем определитель третьего порядка: 6-й этап — четвёртый треугольник

Общий вид формулы для расчёта определителя третьего порядка

Пример расчёта определителя третьего порядка

Транспонированная матрица алгебраических дополнений вычисляется в три шага:

1. Мы из исходной матрицы находим матрицу миноров.
2. Меняем в матрице миноров знак некоторых элементов и получаем матрицу алгебраических дополнений.
3. Находим транспонированную матрицу из матрицы алгебраических дополнений.

Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка.

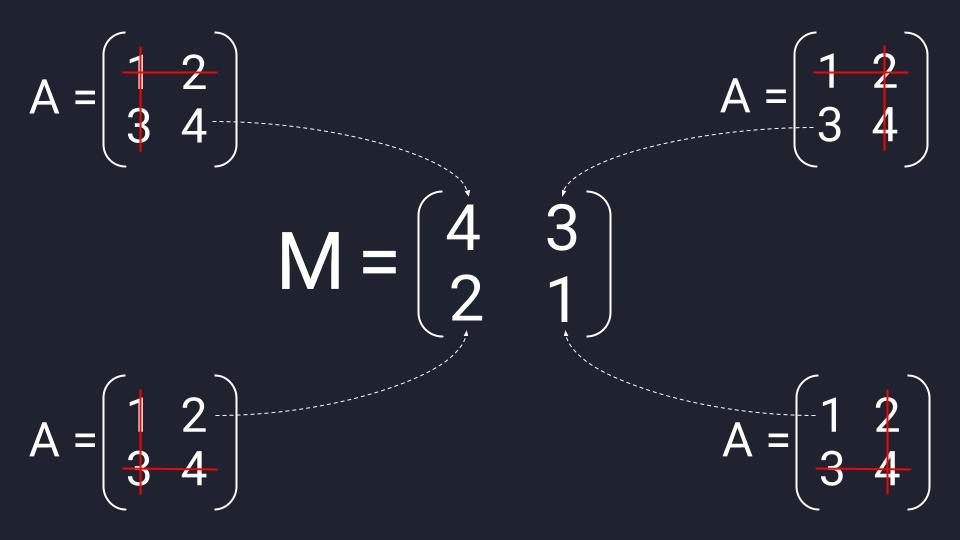
Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы:

• Вычёркиваем первую строку и первый столбец исходной матрицы — получаем первый элемент первой строки матрицы миноров.
• Вычёркиваем первую строку и второй столбец — получаем второй элемент первой строки матрицы миноров.
• Вычёркиваем вторую строку и первый столбец — получаем первый элемент второй строки матрицы миноров.
• Вычёркиваем вторую строку и второй столбец — получаем второй элемент второй строки матрицы миноров.

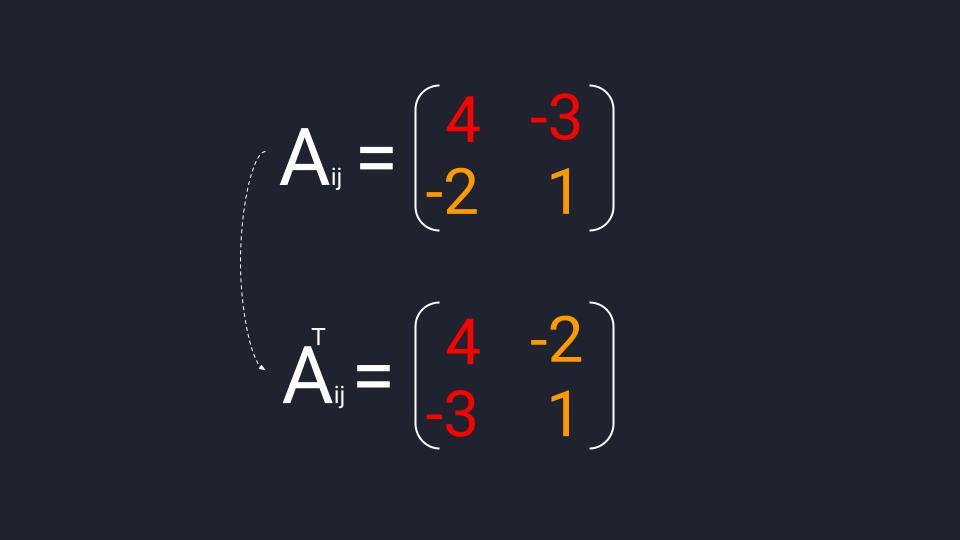
Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.

Пример вычисления матрицы миноров из матрицы второго порядка

Пример вычисления матрицы алгебраических дополнений (Aᵢⱼ ) из матрицы миноров второго порядка

Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров второго порядка

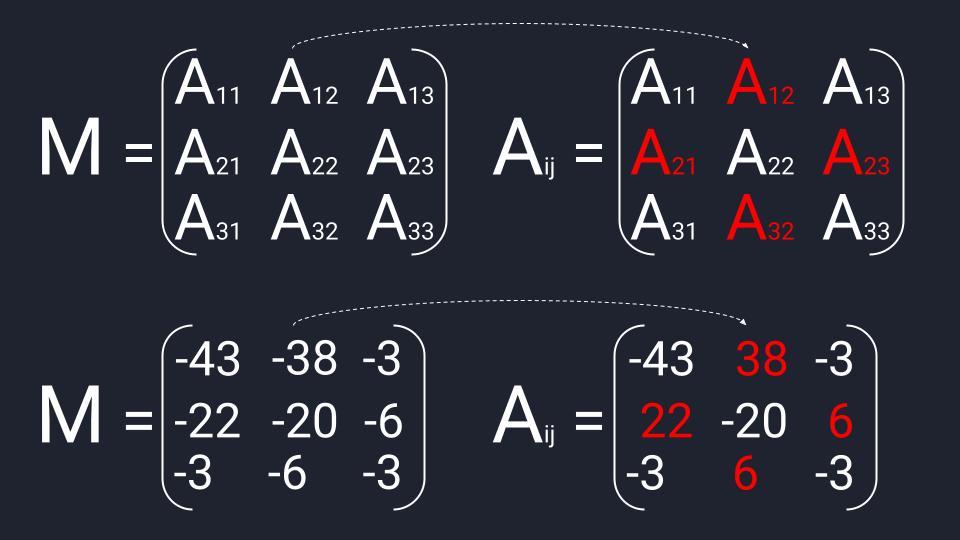
Матрица миноров третьего порядка рассчитывается по следующему принципу:

1. Последовательно вычёркиваем строки и столбцы.
2. Получаем четыре элемента и считаем определитель.
3. Записываем результат в матрицу миноров третьего порядка.

Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему:

1. Определите элемент, который вы ищете для матрицы. Пусть это будет A₁₁.
2. Найдите этот же элемент в исходной матрице и отметьте его точкой.
3. Проведите от этой точки две линии: вдоль строки и вдоль столбца.

После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.

Пример вычисления первого элемента матрицы миноров из матрицы третьего порядка. Треугольник, или греческая дельта, — это обозначение определителя вне матрицы

Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами.

1-я строка 1-й элемент:

1-я строка 2-й элемент:

1-я строка 3-й элемент:

2-я строка 1-й элемент:

2-я строка 2-й элемент:

2-я строка 3-й элемент:

3-я строка 1-й элемент:

3-я строка 2-й элемент:

3-я строка 3-й элемент:

Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.

Получаем из матрицы третьего порядка матрицу миноров

Меняем знаки в матрице миноров и получаем матрицу алгебраических дополнений (Aᵢⱼ)

Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров третьего порядка

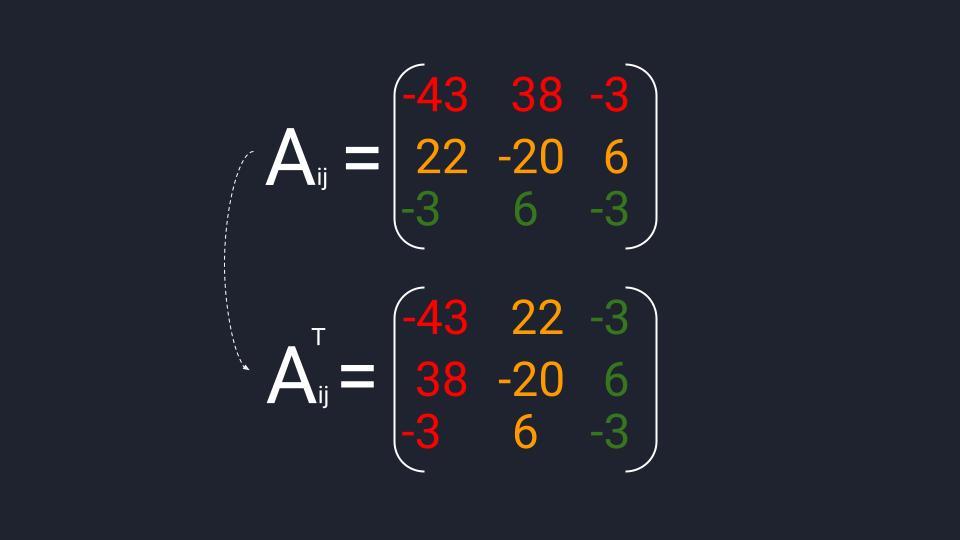
Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:

Пример вычисления обратной матрицы второго порядка: мы внесли дробь в матрицу, но могли этого не делать — просто так захотелось

Пример вычисления обратной матрицы третьего порядка: мы оставили дробь за пределами матрицы и вынесли из матрицы минус. Матрица — это таблица с числами, поэтому не обращайте внимание, если числа получаются большими или неудобными

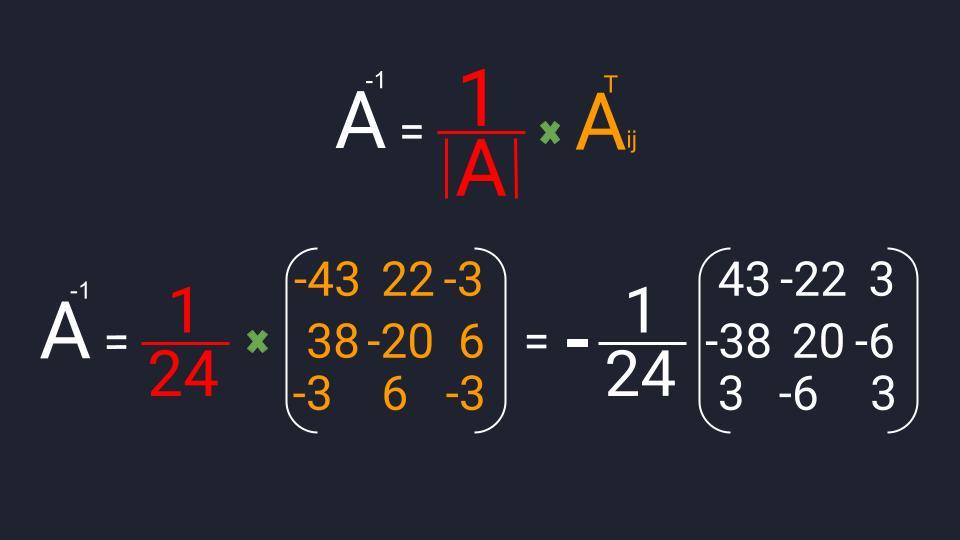
Господи, зачем всё это?

Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь?

• Вам не нужно уметь решать все эти уравнения самостоятельно. Для этого давно есть мощные алгоритмы.
• Достаточно понимать, из чего всё это складывается. Вот матрица. Вот некий алгоритм, который делает из этой матрицы какую-то другую матрицу. Это всё просто арифметика, числа туда, числа сюда.
• В конце этого пути мы покажем, как из этих кубиков собрано машинное обучение. И вы увидите, что машинное обучение — это просто много алгебры. Просто арифметика, числа туда, числа сюда.
• И вы понимаете, что никакого искусственного интеллекта не существует. Это всё, от начала и до конца, работа с числами и расчёты по формулам. Просто когда это делается в больших масштабах, создаётся иллюзия осмысленной деятельности. Ключевое слово — иллюзия.

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Обратная матрица

Для квадратной матрицы $ A_<> $ матрица $ B_<> $ называется левой обратной, если $ BA=E_<> $, где $ E_<> $ — единичная матрица; для матрицы $ A_<> $ матрица $ C_<> $ называется правой обратной если $ AC=E $.

Теорема. Для того, чтобы существовала левая обратная матрица для матрицы $ A_<> $ необходимо и достаточно, чтобы $ \det A_<> \ne 0 $. В этом случае, левая обратная матрица будет единственной и совпадает с правой обратной: $ AB=BA=E $.

Доказательство. Необходимость условия $ \det A_<> \ne 0 $ для существования, например, левой обратной матрицы следует из условия $$ \det (B \cdot A)= \det E \quad \iff \quad (\det B) (\det A) =1 \ . $$

При выполнении условия $ \det A_<> \ne 0 $ можем взять $$ A^<-1>=\frac< \operatorname(A) ><\det A>= \left( \begin \frac> <\det A>& \frac> <\det A>& \dots & \frac> <\det A>\\ &&& \\ \frac> <\det A>& \frac> <\det A>& \dots & \frac> <\det A>\\ &&& \\ \vdots & & & \vdots \\ \frac> <\det A>& \frac> <\det A>& \dots & \frac> <\det A>\end \right) \ . $$ Пока что мы получили правую обратную матрицу: доказано, что она удовлетворяет условию $ A C = E_<> $. Проверка того, что полученная матрица будет являться и левой обратной, т.е. удовлетворяет условию $ C A=E $, производится снова с использованием теоремы о сумме произведений элементов столбца матрицы $ A_<> $ на алгебраические дополнения к другому столбцу той же матрицы (см. теорему $ 2 $ ☞ ЗДЕСЬ ). Теперь покажем, единственность полученной обратной матрицы. Предположим, что каким-то другим способом найдена еще одна матрица $ C_1 $ обладающая тем же самым свойством $ A C_1 = E $. Домножим это равенство слева на матрицу $ C_<> $: $$ C(AC_1) = C E \ . $$ Операция умножения матриц подчиняется ассоциативному закону, поэтому $$ (CA) C_1 = C , $$ но, по доказанному ранее, $ CA=E_<> $. И мы получили равенство $ C_1 = C $, доказывающее единственность правой обратной матрицы. Аналогично доказывается единственность и левой обратной. ♦

Обратную матрицу к матрице $ A_<> $ обозначают $ A_<>^ <-1>$, а сама процедура нахождения такой матрицы называется обращением матрицы $ A_<> $. Матрица, определитель которой отличен от нуля, называется неособенной или невырожденной или обратимой.

Способы построения

1. Первый способ следует из доказательства предыдущей теоремы. Вычислим все алгебраические дополнения к элементам матрицы $ A_<> $, составим из них новую матрицу порядка $ n_<> $ и транспонируем ее. Полученная матрица $$ \operatorname(A) =\left(\left[A_ \right]_^n \right)^ <\top>= \left( \begin A_ <11>& A_<21>& \dots & A_ \\ A_ <12>& A_ <22>& \dots & A_ \\ \dots & & & \dots \\ A_ <1n>& A_ <2n>& \dots & A_ \end \right) $$ называется взаимной или союзной матрице $ A_<> $. При условии $ \det A_<> \ne 0 $ будем иметь: $$ A^<-1>=\frac<\tilde A ><\det A>= \left( \begin \frac> <\det A>& \frac> <\det A>& \dots & \frac> <\det A>\\ &&& \\ \frac> <\det A>& \frac> <\det A>& \dots & \frac> <\det A>\\ &&& \\ \vdots & & & \vdots \\ \frac> <\det A>& \frac> <\det A>& \dots & \frac> <\det A>\end \right) $$

Пример. Вычислить

$$ \left( \begin 4&7& 1 &5 \\ 3 & 4 & 0 &-6 \\ -11 & 8 & 2 & 9\\ -12 & -10 &0 & 8 \end \right)^ <-1>\ . $$

Решение. Вычисляем определитель этой матрицы: $ \det A = -226 \ne 0 $. Обратная матрица существует. Вычисляем алгебраические дополнения элементов: $$ \overbrace<\left| \begin 4 & 0 &-6 \\ 8 & 2 & 9\\ -10 &0 & 8 \end \right|>^>=-56, \ \overbrace<-\left| \begin 3 & 0 &-6 \\ -11 & 2 & 9\\ -12 &0 & 8 \end \right|>^>=96, \overbrace<\left| \begin 3 & 4 &-6 \\ -11 & 8 & 9\\ -12 &-10 & 8 \end \right|>^>=-854, \overbrace<-\left| \begin 3 & 4 & 0 \\ -11 & 8 & 2 \\ -12 & -10 &0 \end \right|>^>=36, $$ $$ A_<21>=-58,\ A_<22>=164,\ A_<23>=-1506,\ A_<24>=118, \dots, A_<44>=58 \ . $$ Cоставляем из них матрицу: $$ \left( \begin -56 & 96 & -854 & 36 \\ -58 & 164 & -1506 & 118 \\ 28&-48 & 314& -9 \\ -40& 117 & -949 & 58 \end \right) \ . $$ и не забываем ее транспонировать, а также поделить на определитель!

2. Второй способ нахождения $ A^<-1>_<> $ часто называют методом Гаусса-Йордана 2) или методом приписывания единичной матрицы. Он, фактически, заключается в одновременном решении семейства систем линейных уравнений $$ AX_1=E_<[1]>, AX_2=E_<[2]>,\dots, AX_n=E_ <[n]>$$ где $ E_<[1]>, E_<[2]>,\dots, E_ <[n]>$ – столбцы единичной матрицы: $$ E_<[1]>=\left( \begin 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end \right),\ E_<[2]>=\left( \begin 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end \right),\dots, E_<[n]>=\left( \begin 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end \right),\ $$ Левые части этих систем одинаковы, поэтому метод исключения переменных Гаусса, примененный к одной, будет действителен и для другой — различия будут проявляться лишь в правых частях. Строго формальное обоснование метода следующее. Рассмотрим систему линейных уравнений относительно неизвестных $ x_1,\dots,x_n,y_1,\dots,y_n $: $$ AX=Y \ . $$ Здесь $ X=(x_1,\dots,x_n)^<\top>, Y=(y_1,\dots,y_n)^ <\top>$. Если $ A_<>^ <-1>$ существует, то эту систему можно разрешить относительно столбца переменных $ X_<> $: $$ X=A^<-1>Y \ . $$ С другой стороны, перепишем ту же систему в матричном виде: $$AX=Y \quad \iff \quad AX=EY \quad \iff \quad \left[A \mid E \right] \left(\begin X \\ -Y \end \right)= \mathbb O_ <2n\times 1>\ ; $$ здесь $ E_<> $ — единичная матрица порядка $ n_<> $. Элементарными преобразованиями над строками матрицы $ \left[A \mid E \right] $ добиваемся того, чтобы в левой ее половине возникла единичная матрица: $ \left[E \mid Q \right] $ (этого всегда можно добиться при условии $ \det A_<>\ne 0 $). Поскольку элементарные преобразования приводят систему линейных уравнений к эквивалентной ей системе (т.е. имеющей то же множество решений), то $$ \left[A \mid E \right] \left(\begin X \\ -Y \end \right)= \mathbb O \quad \iff \quad \left[E \mid Q \right] \left(\begin X \\ -Y \end \right)= \mathbb O \quad \iff \quad X=QY \ . $$ Сравнивая два представления решений системы, приходим к равенству $$ A^<-1>Y = QY $$ справедливому для любого столбца $ Y_<> $. Выбираем $ Y_<> $ из множества столбцов единичной матрицы, получаем: $$ A^<-1>E_<[1]>= QE_<[1]>,\ A^<-1>E_<[2]>= QE_<[2]>,\dots, A^<-1>E_<[n]>= QE_ <[n]>\quad \iff \quad A^<-1>E=QE \quad \iff \quad A^<-1>=Q \ . $$

Алгоритм обращения матрицы посредством приписыванием к ней единичной

1. Осуществляем конкатенацию матриц $ A $ и единичной матрицы $ E $ того же порядка: формируем расширенную $ n\times 2n_<> $-матрицу $ \left[A \mid E \right] $.

2. Элементарными преобразованиями строк расширенной матрицы, добиваемся, чтобы в левой ее половине получилась единичная матрица.

3. Если это удается сделать, то матрица, получившаяся в правой половине и будет $ A_<>^ <-1>$. Если это сделать невозможно, то $ \det A_<>=0 $, т.е. $ A_<>^ <-1>$ не существует.

Пример. Вычислить

$$ \left( \begin 4& 5 &1 \\ 1 & 3 &-2 \\ 3 & 1 & 2 \end \right)^ <-1>$$ приписыванием единичной матрицы.

Решение. $$\left(\begin 4& 5 &1&1&0&0\\ 1 & 3 &-2&0&1&0\\ 3 & 1 & 2&0&0&1 \end\right)\to \left(\begin 1 & 3 &-2&0&1&0\\ 4& 5 &1&1&0&0\\ 3 & 1 & 2&0&0&1 \end\right) \to $$ $$ \to \left(\begin 1&3&-2&0&1&0\\ 0&-7&9&1&-4&0\\ 0&-8&8&0&-3&1 \end\right) \to \left(\begin 1&3&-2&0&1&0\\ 0&-8&8&0&-3&1\\ 0&-7&9&1&-4&0 \end\right) \to $$ $$ \to \left(\begin 1&3&-2&0&1&0\\ 0&-1&1&0&-3/8& 1/8\\ 0&-7&9&1&-4&0 \end\right)\to \left(\begin 1&3&-2&0&1&0\\ 0&-1&1&0&-3/8& 1/8\\ 0&0&2&1&-11/8&-7/8 \end\right) \to $$ $$ \to \left(\begin 1&3&-2&0&1&0\\ 0&-1&1&0&-3/8& 1/8\\ 0&0&1&1/2&-11/16& -7/16 \end\right)\to $$ $$ \to \left(\begin 1&3&-2&0&1&0\\ 0&-1&0&-1/2& 5/16& 9/16\\ 0&0&1&1/2&-11/16&-7/16 \end\right)\to $$ $$ \to \left(\begin 1&0&0&-1/2& 9/16 &13/16\\ 0&1&0&1/2&-5/16& -9/16\\ 0&0&1&1/2&-11/16&-7/16 \end\right) . $$

Ответ. $$ \left( \begin -1/2& 9/16 & 13/16 \\ 1/2&-5/16 & -9/16 \\ 1/2&-11/16 &-7/16 \end \right) $$

Алгоритм шифрования Rijndael, используемый в мобильной телефонии, имеет в одной из стадий следующее преобразование байтов

$$ \begin y_0 \\ y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ y_6 \\ y_7 \end = \begin 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \end \begin x_0 \\ x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \end + \begin 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 \end \pmod <2>$$ Найти обратное преобразование.

Ответ ☞ ЗДЕСЬ.

3. Этот способ основан на теореме Гамильтона-Кэли. Если найден характеристический полином матрицы $ A_<> $: $$ \det(A-\lambda E)\equiv (-1)^n (\lambda^n + a_1 \lambda^ + \dots + a_\lambda + a_n ) \, $$ то при условии $ a_n \ne 0 $ матрица $ A_<> $ обратима и $$ A^<-1>= — \frac<1> \left( A^+a_1 A^ + \dots + a_ E \right) \ , $$ т.е. $ A^ <-1>$ может быть вычислена посредством возведения в степень матрицы $ A_<> $.

Свойства операции обращения

Если в левой части каждого каждого из следующих равенств операции определены, то равенства справедливы:

Использование для решения систем линейных уравнений

Рассмотрим систему линейных уравнений с квадратной матрицей $ A $, т.е. такую, у которой число уравнений совпадает с числом неизвестных: $$ \left\<\begin a_<11>x_1 +a_<12>x_2+\ldots+a_<1n>x_n &=&b_1\\ a_<21>x_1 +a_<22>x_2+\ldots+a_<2n>x_n &=&b_2\\ \ldots& & \ldots \\ a_x_1 +a_x_2+\ldots+a_x_n &=&b_n \end\right. \quad \iff \quad AX= <\mathcal B>$$ Теорема Крамера утверждает, что такая система имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля: $ \det A \ne 0 $. Это же условие является необходимым и достаточным и для существования обратной матрицы $ A^ <-1>$. Но тогда решение системы можно записать в матричной форме: $$ X=A^ <-1> <\mathcal B>\ , $$ и такое представление бывает удобно в тех задачах, в которых требуется решить семейства систем с одинаковой матрицей $ A $, но различными столбцами правых частей $ <\mathcal B>$. Как соотносятся формулы Крамера и только что полученная формула? — Для пояснения, распишем первую компоненту решения, воспользовавшись представлением обратной матрицы по способу 1 ( см. ☞ ЗДЕСЬ ). Имеем: $$ x_1 = \frac> <\det A>b_1 + \frac> <\det A>b_2 + \dots + \frac> <\det A>b_n $$ Но полученное выражение совпадает с разложением определителя $$ \frac<1> <\det A>\left| \begin b_ <1>& a_ <12>& \dots & a_ <1n>\\ b_ <2>& a_ <22>& \dots & a_ <2n>\\ \dots &&& \dots \\ b_ & a_ & \dots & a_ \end \right| $$ по первому столбцу, т.е. мы получили первую из формул Крамера.

Обратные к конкретным типам матриц

1. треугольной матрице (верхней или нижней), если существует, то будет треугольной матрицей (того же типа);

2. симметричной матрице, если существует, то будет симметричной матрицей;

3. кососимметричной матрице нечетного порядка не существует, а в случае четного порядка, если существует, то будет кососимметричной матрицей;

4. ортогональной матрице $ Q_<> $ всегда существует и получается транспонированием матрицы: $ Q^ <-1>= Q^ <\top>$.

5. квадратной матрице Вандермонда $$ \left( \begin 1& 1& \ldots& 1\\ x_1& x_2& \ldots& x_n\\ x_1^2& x_2^2& \ldots& x_n^2\\ \vdots& \vdots& & \vdots \\ x_1^& x_2^& \ldots& x_n^ \end \right) $$ существует тогда и только тогда, когда все $ x_1,\dots,x_n $ различны. Выражение ☞ ЗДЕСЬ.

В некоторых приложениях важно по виду матрицы быстро определить существует ли у нее обратная — без непосредственного нахождения этой обратной. Для некоторых типов матриц можно получить «вычислительно дешевые» критерии отличия их определителей от нуля.

Следующая теорема основана на связи определителя матрицы с ее собственными числами.

Теорема. Матрица $ A_<> $, у которой элементы каждой строки обладают свойством

$$ |a_|>|a_|+\dots+|a_|+|a_|+\dots+|a_| \quad npu \quad \forall j\in \ <1,\dots,n\>$$ (модуль элемента на главной диагонали больше суммы модулей остальных элементов строки) называется матрицей с диагональным доминированием (преобладанием). Такая матрица всегда обратима.

Доказательство следует из того факта, что $ \det A_<> \ne 0 $ тогда и только тогда, когда в наборе собственных чисел матрицы 3) $ A_<> $ нет нулевого (см. следствие к теореме 1 ☞ ЗДЕСЬ ). Локализовать собственные числа матрицы можно с помощью теоремы Гершгорина: любое собственное число $ \lambda_<> $ матрицы $ A_<> $ должно удовлетворять хотя бы одному неравенству $$ |\lambda — a_| ♦

Обращение блочных матриц

Теорема [Фробениус]. 4) . Пусть имеется блочная квадратная матрица вида

$$ \left( \begin A & B \\ C & D \end \right) \quad , $$ где матрица $ A_<> $ — квадратная порядка $ k_<> $, а матрица $ D_<> $ — квадратная порядка $ \ell_<> $. Тогда $$\left( \begin A & B \\ C & D \end \right)^<-1>= \left( \begin A^ <-1>+A^<-1>BK^<-1>CA^ <-1>& -A^<-1>BK^ <-1>\\ -K^<-1>CA^ <-1>& K^ <-1>\end \right) \ , $$ где матрица $$ K=D-CA^<-1>B $$ называется шуровским дополнением 5) к подматрице $ A_<> $. Здесь предполагается, что матрицы $ A_<> $ и $ K_<> $ — неособенные.

При $ B=\mathbb O $ имеем:

$$ \left( \begin A & \mathbb O \\ C & D \end \right)^<-1>= \left( \begin A^ <-1>& \mathbb O \\ -D^<-1>CA^ <-1>& D^ <-1>\end \right) \ , $$ если матрицы $ A_<> $ и $ D_<> $ — неособенные.

Доказательство. Будем искать $$ \left( \begin A & \mathbb O \\ C & D \end \right)^ <-1>$$ в виде $$ \left( \begin X & Y \\ U & V \end \right)_ $$ при $ k\times k $-матрице $ X $ и $ \ell\times \ell $-матрице $ V $. Разбиваем матричное равенство $$ \left( \begin X & Y \\ U & V \end \right) \left( \begin A & \mathbb O \\ C & D \end \right) =\left( \begin E_k & \mathbb O \\ \mathbb O & E_ <\ell>\end \right) $$ на четыре отдельных $$ \begin XA+YC=E_k, & YD=\mathbb O, \\ UA+VC=\mathbb O, & VD=E_ <\ell>\end \quad \Rightarrow \quad \begin Y=\mathbb O, \\ V=D^<-1>. \end $$ Подставляем полученное в два оставшихся равенства: $ X=A^ <-1>$, $ U=-D^<-1>CA^ <-1>$. ♦

Найти обратную матрицу для матрицы Фробениуса

$$ <\mathfrak F>= \left( \begin 0 & 1 & 0 & 0 & \dots & 0 & 0 \\ 0 & 0 & 1 & 0 & \dots & 0 & 0 \\ 0 & 0 & 0 & 1 & \dots & 0 & 0 \\ \dots& &&&\ddots & & \dots \\ 0 & 0 & 0 & 0 & \dots & 0 & 1 \\ a_n & a_ & a_ & & \dots & a_2 & a_1 \end \right)_ $$

Решение и ответ ☞ ЗДЕСЬ

Обращение «возмущенных» матриц

Довольно часто ставится задача нахождения обратной к матрице $ A+B_<> $ при условии, что известна матрица $ A^ <-1>$ и доступна некоторая дополнительная информация о «возмущении» — о матрице $ B_<> $.

Следующий результат формулируем только для случая вещественных матриц, хотя существует его обобщение для комплексных.

Теорема [Шерман, Моррисон]. [3]. Пусть матрицы

Особенно полезен этот результат для случая возмущения матрицы $ A_<> $ посредством матриц одноранговых:

Вычислить $ (A+B)^ <-1>$ для

$$ A=\left(\begin -7 & 22 & — 55 \\ -94 & 87 & -56 \\ 0 & -62 & 97 \end \right), \ B=\left(\begin 1 & 1 & 2 \\ 0 & 1 & 1 \\ -1 & 0 & -1 \end \right) \ , $$ если известно, что $$ A^ <-1>= \frac<1> <154713>\left(\begin -4967 & -1276 & — 3553 \\ -9118 & 679 & -4778 \\ -5828 & 434 & -1459 \end \right) \ . $$

Используется в модифицированном симплекс-методе, в котором на каждом шаге требуется вычислять обратную матрицу для матрицы, которая отличается от матрицы, полученной на предыдущем шаге только в одном столбце [4].

Псевдообратная матрица

Эта матрица определяется не только для квадратной матрицы $ A_<> $.

Пусть сначала матрица $ A_<> $ порядка $ m\times n_<> $ — вещественная и $ m \ge n_<> $ (число строк не меньше числа столбцов). Если $ \operatorname (A) = n $ (столбцы матрицы линейно независимы), то псевдообратная к матрице $ A_<> $ определяется как матрица $$ A^<+>=(A^<\top>A)^ <-1>A^ <\top>\ . $$ Эта матрица имеет порядок $ n \times m_<> $. Матрица $ (A^<\top>A)^ <-1>$ существует ввиду того факта, что при условии $ \operatorname (A) = n $ будет выполнено $ \det (A^ <\top>A) > 0 $ (см. теорему $ 2 $ в пункте ☞ ТЕОРЕМА БИНЕ-КОШИ или же пункт ☞ СВОЙСТВА ОПРЕДЕЛИТЕЛЯ ГРАМА ). Очевидно, что $ A^ <+>\cdot A = E_ $, т.е. псевдообратная матрица является левой обратной для матрицы $ A_<> $. В случае $ m=n_<> $ псевдообратная матрица совпадает с обратной матрицей: $ A^<+>=A^ <-1>$.

Пример. Найти псевдообратную матрицу к матрице

$$ A= \left( \begin 1 & 0 \\ 0 & 1 \\ 1 & 1 \end \right) \ . $$

Решение. $$ A^<\top>= \left( \begin 1 & 0 & 1 \\ 0 & 1 & 1 \end \right) \quad \Rightarrow \quad A^ <\top>\cdot A = \left( \begin 2 & 1 \\ 1 & 2 \end \right) \quad \Rightarrow \quad (A^ <\top>\cdot A)^ <-1>= \left( \begin 2/3 & -1/3 \\ -1/3 & 2/3 \end \right) \ \Rightarrow $$ $$ \Rightarrow \ A^ <+>= (A^ <\top>\cdot A)^ <-1>A^ <\top>= \left( \begin 2/3 & -1/3 & 1/3 \\ -1/3 & 2/3 & 1/3 \end \right) \ . $$ При этом $$ A^ <+>\cdot A = \left( \begin 1 & 0 \\ 0 & 1 \end \right),\quad A \cdot A^ <+>= \left( \begin 2/3 & -1/3 & 1/3 \\ -1/3 & 2/3 & 1/3 \\ 1/3 & 1/3 & 2/3 \end \right) \ , $$ т.е. матрица $ A^ <+>$ не будет правой обратной для матрицы $ A_<> $. ♦

Вычислить псевдообратную матрицу для $$ \mathbf\ \left( \begin 1 & 0 \\ 1 & 1 \\ 1 & 1 \end \right) \quad ; \quad \mathbf\ \left( \begin x_1 \\ x_2 \\ x_3 \end \right) \ . $$

Концепция псевдообратной матрицы естественным образом возникает из понятия псевдорешения системы линейных уравнений. Если $ A^ <+>$ существует, то псевдорешение (как правило, переопределенной и несовместной!) системы уравнений $ AX=\mathcal B_<> $ находится по формуле $ X= A^ <+>\mathcal B $ при любом столбце $ \mathcal B_<> $. Верно и обратное: если $ E_<[1]>, E_<[2]>,\dots, E_ <[m]>$ – столбцы единичной матрицы $ E_m $: $$ E_<[1]>=\left( \begin 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end \right),\ E_<[2]>=\left( \begin 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end \right),\dots, E_<[m]>=\left( \begin 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end \right),\ $$ а псевдорешение системы уравнений $ AX=E_ <[j]>$ обозначить $ X_ $ (оно существует и единственно при условии $ \operatorname (A) = n $), то $$ A^<+>=\left[X_1,X_2,\dots,X_m \right] \ . $$

Теорема. Пусть $ A \in \mathbb R^ $, $ m \ge n_<> $ и $ \operatorname (A) = n $. Тогда псевдообратная матрица $ A^ <+>$ является решением задачи минимизации

$$ \min_> ||AX-E_m||^2 $$ где $ || \cdot || $ означает евклидову норму (норму Фробениуса) матрицы : $$ ||[h_]_||^2=\sum_ h_^2 \ . $$ При сделанных предположениях решение задачи единственно.

С учетом этого результата понятно как распространить понятие псевдообратной матрицы на случай матрицы $ A \in \mathbb R^ $, у которой число строк меньше числа столбцов: $ m ☞ ЗДЕСЬ.

Источники

[1]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ.1960, с.187-192

[2]. Беклемишев Д.В. Дополнительные главы линейной алгебры. М.Наука.1983, с.187-234

[3]. Gill P.E., Murray W., Wright M.H. Numerical Linear Algebra and Optimization. V.1. Addison-Wesley, NY, 1991

[4]. Таха Х. Введение в исследование операций. Т.1, глава 7. М.Мир. 1985