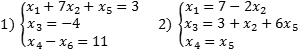Общая теория системы алгебраических уравнений

Системы линейных уравнений: основные понятия

— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

— это последовательность чисел ( k ₁, k ₂, . k_n ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x ₁, x ₂, . x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

1. Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
2. Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
3. Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.

Переменная x_i называется , если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной x_i должен быть равен нулю.

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x ₁, x ₃ и x ₄. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x ₁, x ₃ и x ₅. Достаточно переписать самое последнее уравнение в виде x ₅ = x ₄.

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:

1. Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x ₁ = b ₁, x ₂ = b ₂, . x_k = b_k ;
2. Число разрешенных переменных r меньше общего числа переменных k : r k . Остальные ( k − r ) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Так, в приведенных выше системах переменные x ₂, x ₅, x ₆ (для первой системы) и x ₂, x ₅ (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.

Теорема. Если в системе из n уравнений переменные x ₁, x ₂, . x_r — разрешенные, а x _{r + 1}, x _{r + 2}, . x _k — свободные, то:

1. Если задать значения свободным переменным ( x _{r + 1} = t _{r + 1}, x _{r + 2} = t _{r + 2}, . x_k = t_k ), а затем найти значения x ₁, x ₂, . x_r , получим одно из решений.
2. Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.

И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.

Общая теория систем линейных уравнений

Условия совместности.

Займемся изучением систем из m уравнений с n неизвестными. Систему
\begina_<1>^<1>x^<1>+a_<2>^<1>x^<2>+. +a_^<1>x^=b^<1>,\\a_<1>^<2>x^<1>+a_<2>^<2>x^<2>+. +a_^<2>x^=b^<2>,\\\cdots\\a_<1>^x^<1>+a_<2>^x^<2>+. +a_^x^=b^\end мы можем кратко записать в виде \tag <1>A\boldsymbol=\boldsymbol.
Система задается своей расширенной матрицей A^ <*>, получаемой объединением матрицы системы A и столбца свободных членов \boldsymbol .

Простое и эффективное условие, необходимое и достаточное для совместности системы (1) , дает следующая теорема, называемая теоремой Кронекера-Капелли.

Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Иначе утверждение теоремы можно сформулировать так: приписывание к матрице A размеров m \times n столбца \boldsymbol высоты m не меняет ее ранга тогда и только тогда, когда этот столбец — линейная комбинация столбцов A .

Если \mathbf\,A^ <*>= \mathbf\,A , то базисный минор A является базисным и для A^ <*>. Следовательно, \boldsymbol раскладывается по базисным столбцам A . Мы можем считать его линейной комбинацией всех столбцов A , добавив недостающие столбцы с нулевыми коэффициентами.

Обратно, если \boldsymbol раскладывается по столбцам A , то элементарными преобразованиями столбцов можно превратить A^ <*>в матрицу A_ <0>, получаемую из A приписыванием нулевого столбца. Из утверждения о том, что ранг матрицы не меняется при элементарных преобразованиях, следует \mathbf\,A_ <0>= \mathbf\,A^ <*>. С другой стороны, \mathbf\,A_ <0>= \mathbf\,A , так как добавление нулевого столбца не может создать новых невырожденных подматриц. Отсюда \mathbf\,A = \mathbf\,A^ <*>, как и требовалось.

Иначе это утверждение можно сформулировать так.

Система линейных уравнений несовместна тогда и только тогда, когда противоречивое равенство 0=1 является линейной комбинацией ее уравнений.

Равенство рангов матрицы системы и расширенной матрицы можно выразить, понимая ранг матрицы как строчный ранг. Это приведет нас к важной теореме, известной как теорема Фредгольма.

Транспонируем матрицу A системы (1) и рассмотрим систему из n линейных уравнений \tag <2>\begin a_<1>^<1>y_<1>+a_<1>^<2>y_<2>+. +a_<1>^y_=0,\\ a_<2>^<1>y_<1>+a_<2>^<2>y_<2>+. +a_<2>^y_=0,\\\cdots\\a_^<1>y_<1>+a_^<2>y_<2>+. +a_^y_=0\end с m неизвестными, матрицей A^и свободными членами, равными нулю. Она называется сопряженной однородной системой для системы (1) . Если \boldsymbol — столбец высоты m из неизвестных, то систему (2) можно записать как A^\boldsymbol=\boldsymbol , или лучше в виде \tag <3>\boldsymbol^A=\boldsymbol, где \boldsymbol — нулевая строка длины n .

Для того чтобы система (1) была совместна, необходимо и достаточно, чтобы каждое решение сопряженной однородной системы (3) удовлетворяло уравнению \tag <4>\boldsymbol^\boldsymbol=y_<1>b^<1>+. +y_b^=0.

1^ <\circ>. Пусть система (1) совместна, то есть существует столбец \boldsymbol высоты n , для которого A\boldsymbol=\boldsymbol . Тогда для любого столбца \boldsymbol высоты m выполнено \boldsymbol^A\boldsymbol=\boldsymbol^\boldsymbol . Если \boldsymbol — решение системы (3) , то \boldsymbol^\boldsymbol=(\boldsymbol^A)\boldsymbol=\boldsymbol\boldsymbol=0 .

2^ <\circ>. Предположим теперь, что система (1) несовместна. Тогда согласно утверждению 1 строка \begin 0&. & 0& 1 \end входит в упрощенный вид расширенной матрицы A^<*>=\begin A& |& \boldsymbol \end и, следовательно, является линейной комбинацией ее строк. Обозначим коэффициенты этой линейной комбинации y_<1>. y_ и составим из них столбец \boldsymbol . Для этого столбца \boldsymbol^\begin A& |& \boldsymbol \end=\begin 0&. & 1 \end (согласно данного утверждения). Это же равенство можно расписать как два: \boldsymbol^A=\boldsymbol и \boldsymbol^\boldsymbol=1 . Итак, нам удалось найти решение системы (3) , не удовлетворяющее условию (4) . Это заканчивает доказательство.

В качестве примера применим теорему Фредгольма к выводу условия параллельности двух различных прямых на плоскости. Их уравнения составляют систему A_<1>x+B_<1>y+C_<1>=0,\ A_<2>x+B_<2>y+C_<2>=0.
Она не имеет решений, если существуют такие числа y_<1>, y_ <2>, что y_<1>A_<1>+y_<2>A_<2>=0 , y_<1>B_<1>+y_<2>B_<2>=0 , но y_<1>C_<1>+y_<2>C_ <2>\neq 0 . Ясно, что y_ <1>и y_ <2>не равны нулю. Поэтому можно положить \lambda=-y_<2>/y_ <1>и записать полученное условие в виде: существует число \lambda такое, что A_<1>=\lambda A_ <2>, B_<1>=\lambda B_ <2>и C_ <1>\neq \lambda C_ <2>.

Нахождение решений.

В этом пункте мы будем предполагать, что дана совместная система из m линейных уравнений с n неизвестными. Ранг матрицы системы обозначим r . Поскольку ранг расширенной матрицы тоже равен r , мы можем считать базисные столбцы матрицы системы базисными столбцами расширенной матрицы. Элементарными преобразованиями строк приведем расширенную матрицу к упрощенному виду (возможность этого мы уже доказывали). Наша система линейных уравнений перейдет в эквивалентную ей систему из r линейно независимых уравнений.

Для удобства записи будем предполагать, что первые r столбцов — базисные. Тогда преобразованную систему можно записать в виде \tag <5>\begin x^<1>=\beta^<1>-(\alpha_^<1>x^+. +\alpha_^<1>x^),\\\cdots\\x^=\beta^-(\alpha_^x^+. +\alpha_^x^).\end
Здесь \alpha_^ и \beta^ — элементы преобразованной расширенной матрицы. В левых частях равенств мы оставили неизвестные, соответствующие выбранным нами базисным столбцам, так называемые базисные неизвестные. Остальные неизвестные, называемые параметрическими, перенесены в правые части равенств.

Как бы мы ни задали значения параметрических неизвестных, по формулам (5) мы найдем значения базисных так, что они вместе со значениями параметрических неизвестных образуют решение системы (1) . Легко видеть, что так мы получим все множество решений.

На формулах (5) можно было бы и остановиться, но ниже мы дадим более простое и наглядное, а также принципиально важное описание совокупности решений системы линейных уравнений.

Приведенная система.

Сопоставим системе линейных уравнений (1) однородную систему с той же матрицей коэффициентов: \tag<6>A\boldsymbol=\boldsymbol. По отношению к системе (1) она называется приведенной.

Пусть \boldsymbol_ <0>— решение системы (1) . Столбец \boldsymbol также будет ее решением тогда и только тогда, когда найдется такое решение у приведенной системы (6) , что \boldsymbol=\boldsymbol_<0>+\boldsymbol .

Пусть \boldsymbol — решение системы (1) . Рассмотрим разность \boldsymbol=\boldsymbol-\boldsymbol_ <0>. Для нее A\boldsymbol=A\boldsymbol-A\boldsymbol_<0>=\boldsymbol-\boldsymbol=\boldsymbol .

Обратно, если \boldsymbol — решение системы (6) , и \boldsymbol=\boldsymbol_<0>+\boldsymbol , то A\boldsymbol=A\boldsymbol_<0>+A\boldsymbol=\boldsymbol+\boldsymbol=\boldsymbol .

Это предложение сводит задачу описания множества решений совместной системы линейных уравнений к описанию множества решений ее приведенной системы.

Однородная система совместна. Действительно, нулевой столбец является ее решением. Это решение называется тривиальным.

Пусть столбцы матрицы A линейно независимы, то есть \mathbf\,A=n . Тогда система (6) имеет единственное решение (ранее мы это уже доказывали) и, следовательно, нетривиальных решений не имеет.

Если \boldsymbol_ <1>и \boldsymbol_ <2>— решения однородной системы, то любая их линейная комбинация — также решение этой системы.

Действительно, из A\boldsymbol_<1>=\boldsymbol и A\boldsymbol_<2>=\boldsymbol для любых \alpha и \beta следует A(\alpha \boldsymbol_<1>+\beta \boldsymbol_<2>)=\alpha A \boldsymbol_<1>+\beta A\boldsymbol_<2>=\boldsymbol .

Если однородная система имеет нетривиальные решения, то можно указать несколько линейно независимых решений таких, что любое решение является их линейной комбинацией. Сделаем это.

Матрица F , состоящая из столбцов высоты n , называется фундаментальной матрицей для однородной системы с матрицей А, если:

1. AF=O ;
2. столбцы F линейно независимы;
3. ранг F максимален среди рангов матриц, удовлетворяющих условию 1).

Столбцы фундаментальной матрицы называются фундаментальной системой решений.

Если фундаментальная матрица существует, то каждый ее столбец в силу первого условия определения — решение системы. Если система не имеет нетривиальных решений, то фундаментальной матрицы нет. Это будет в том случае, когда столбцы А линейно независимы: \mathbf\,A=n .

Ниже мы докажем, что в остальных случаях фундаментальная матрица существует, но сначала выясним, что означает третье условие в определении.

Пусть A — матрица размеров m \times n и ранга r . Если AF=O , то \mathbf\,F \leq n-r .

Приведем матрицу A к упрощенному виду элементарными преобразованиями строк, а затем элементарными преобразованиями столбцов обратим в нулевые все небазисные столбцы. Мы получим матрицу A’=PAQ , где P и Q — произведения соответствующих элементарных матриц. Первые r строк A’ — строки единичной матрицы порядка n , а остальные — нулевые. Обозначим F’=Q^<-1>F . Тогда \mathbf\,F’ = \mathbf\,F . Используя ранее доказанное нами утверждение, легко заметить, что первые r строк матрицы A’F’ совпадают с первыми r строками F’ . Но A’F’=PAF=O и, следовательно, F’ содержит r нулевых строк. Так как всего в ней n строк, \mathbf\,F’ \leq n-r . Это равносильно доказываемому утверждению.

Покажем теперь, как может быть построена фундаментальная матрица. Согласно ранее доказанному утверждению, решение однородной системы состоит из коэффициентов равной нулю линейной комбинации столбцов матрицы системы. Мы можем получить такие линейные комбинации, основываясь на теореме о базисном миноре. Снова для удобства записи будем считать, что в матрице A первые r столбцов — базисные. Каждый из небазисных столбцов \boldsymbol_ (j=r+1. n) раскладывается по базисным: \tag <7>\boldsymbol_=\alpha_^<1>\boldsymbol_<1>+. +\alpha_^\boldsymbol_. Отсюда следует, что столбец \begin -\alpha_^<1>. -\alpha_^& 0. 0& 1& 0. 0 \end^решением. (Единица в нем стоит на j -м месте.)

Таких решений можно составить столько, сколько есть небазисных столбцов, то есть (n-r) . Убедимся в том, что эти решения линейно независимы. Для этого объединим все столбцы в одну матрицу \tag <8>\begin -\alpha_^<1>& -\alpha_^<1>&. -\alpha_^<1>,\\\cdots\\-\alpha_^& -\alpha_^&. -\alpha_^,\\1& 0&. & 0\\0& 1&. & 0\\\cdots\\0& 0&. & 1\end.
Подматрица в последних n-r строках — единичная. Поэтому ранг матрицы (8) равен числу столбцов, и столбцы линейно независимы.

Таким образом, мы получили

Если ранг матрицы однородной системы линейных уравнений r меньше числа неизвестных n , то система имеет фундаментальную матрицу из n-r столбцов.

Итак, система столбцов (8) — фундаментальная система решений. Она называется нормальной фундаментальной системой решений. Каждому выбору базисных столбцов соответствует своя нормальная фундаментальная система решений. Вообще же, каждая система из n-r линейно независимых решений является фундаментальной.

Для нахождения матрицы (8) можно привести матрицу A системы к упрощенному виду, что даст коэффициенты разложения небазисных столбцов по базисным.

Пусть F — фундаментальная матрица системы A\boldsymbol=\boldsymbol . Рассмотрим произвольный столбец с высоты n-r . Произведение F\boldsymbol — столбец высоты n , и из равенства AF\boldsymbol =\boldsymbol следует, что при любом с столбец F\boldsymbol — решение системы. Оказывается, имеет место

Столбец \boldsymbol — решение системы A\boldsymbol=\boldsymbol тогда и только тогда, когда существует такой столбец \boldsymbol , что \tag <9>\boldsymbol=F\boldsymbol.

Остается доказать необходимость условия. Пусть \boldsymbol — решение. Присоединив его к F , получим матрицу F^<*>=\begin F\ |\ \boldsymbol \end . Эта матрица удовлетворяет условию AF^<*>=O , так как каждый ее столбец — решение. Значит, \mathbf\,F^<*>=n-r . По теореме Кронекера-Капелли мы заключаем отсюда, что существует столбец \boldsymbol , удовлетворяющий системе F\boldsymbol=\boldsymbol .

Общее решение системы линейных уравнений.

Теперь мы можем собрать воедино наши результаты — утверждения 2 и 6.

Выражение, стоящее в правой части формулы (10) , называется общим решением системы линейных уравнений. Если \boldsymbol_<1>. \boldsymbol_ — фундаментальная система решений, а c_<1>. c_ — произвольные постоянные, то формула (10) может быть написана так: \tag <11>\boldsymbol=\boldsymbol_<0>+c_<1>\boldsymbol_<1>+. +c_\boldsymbol_.

Теорема 3 верна, в частности, и для однородных систем. Если \boldsymbol_ <0>— тривиальное решение, то (10) совпадает с (9) .

Одна из ранее доказанных нами теорем гласит, что для существования единственного решения системы из n линейных уравнений с n неизвестными достаточно, чтобы матрица системы имела детерминант, отличный от нуля. Сейчас легко получить и необходимость этого условия.

Пусть A — матрица системы из n линейных уравнений с n неизвестными. Если \det A=0 , то система либо не имеет решения, либо имеет бесконечно много решений.

Равенство \det A=0 означает, что \mathbf\,A и, следовательно, приведенная система имеет бесконечно много решений. Если данная система совместна, то из теоремы 3 следует, что и она имеет бесконечно много решений.

Пример.

Рассмотрим уравнение плоскости как систему \tag<12>Ax+By+Cz+D=0 из одного уравнения. Пусть A \neq 0 и потому является базисным минором матрицы системы. Ранг расширенной матрицы 1, значит, система совместна. Одно ее решение можно найти, положив параметрические неизвестные равными нулю: y=z=0 . Мы получим x=-D/A . Так как n=3 , r=1 , фундаментальная матрица имеет два столбца. Мы найдем их, придав параметрическим неизвестным два набора значений: y=1 , z=0 и y=0 , z=1 . Соответствующие значения базисной неизвестной x , найденные из приведенной системы, будут -B/A и -C/A . Итак, общее решение системы (12) \tag <13>\begin x\\ y\\ z \end=\begin -D/A\\ 0\\ 0 \end+c_ <1>\begin -B/A\\ 1\\ 0 \end+c_ <2>\begin -C/A\\ 0\\ 1 \end.

Выясним геометрический смысл полученного решения. Очевидно, прежде всего, что решение \begin -D/A& 0& 0 \end^состоит из координат некоторой (начальной) точки плоскости, или, что то же, из компонент ее радиус-вектора. В формуле (10) решение x_0 можно выбирать произвольно. Это соответствует произволу выбора начальной точки плоскости. Мы уже знаем, что компоненты лежащих в плоскости векторов удовлетворяют уравнению A\alpha_<1>+B\alpha_<2>+C\alpha_<3>=0 , то есть приведенной системе. Два линейно независимых решения этой системы (фундаментальная система решений) могут быть приняты за направляющие векторы плоскости. Таким образом, формула (13) — не что иное, как параметрические уравнения плоскости.

Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений с неизвестными называется система уравнений вида

Числа называются коэффициентами системы ; — свободными членами , — неизвестными . Количество уравнений в системе может быть меньше, больше или равно числу неизвестных.

Решением системы называется упорядоченная совокупность чисел такая, что после замены неизвестных соответственно числами каждое уравнение системы превращается в верное числовое равенство. Система называется совместной , если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной .

Система (5.1) называется однородной , если все свободные члены равны нулю:

В отличие от однородной, систему общего вида (5.1) называют неоднородной .

Систему (5.1) принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы

свободные члены записываем в столбец свободных членов

а неизвестные — в столбец неизвестных

Матричная запись неоднородной системы уравнений (5.1) имеет вид

Матричную запись (5.3) системы уравнений можно представить в эквивалентной форме

Тогда решение системы представляется столбцом и удовлетворяет равенству

т.е. столбец свободных членов является линейной комбинацией столбцов матрицы системы.

Относительно системы уравнений нас интересуют ответы на следующие вопросы:

1. Совместна система или нет?

2. Если система совместна, то имеет ли она единственное решение или нет?

3. Если решение единственное, то как его найти?

4. Если система имеет бесконечно много решений, то какова структура множества решений?

5. Как в бесконечном множестве решений системы определить одно решение, наилучшее с практической точки зрения?

6. Если система несовместна, то как определить ее приближенное решение?

Правило Крамера

Рассмотрим случай, когда число уравнений равно числу неизвестных , т.е. систему

где матрица системы — квадратная n-го порядка:

Ее определитель обозначим

Теорема 5.1 (правило Крамера). Если определитель матрицы системы линейных уравнений с неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам

где — определитель матрицы, полученной из матрицы системы заменой i-го столбца столбцом свободных членов, т.е.

В самом деле, рассмотрим систему (5.6) как матричное уравнение . Так как определитель матрицы отличен от нуля, по теореме 4.2 заключаем, что матричное уравнение имеет единственное решение:

где — обратная матрица. Запишем i-й элемент столбца , учитывая, что в i-й строке присоединенной матрицы стоят алгебраические дополнения i-го столбца матрицы

Заметим, что в скобках записано разложение определителя по i-му столбцу, т.е. , что и требовалось доказать.

1. На практике при больших правило Крамера не применяется, так как вычисление определителя n-го порядка требует большого числа арифметических операций. Поэтому применяются более экономичные алгоритмы. Обычно, правило Крамера используется, когда нужно найти только несколько неизвестных (например, одну) среди многих. В теоретических исследованиях правило Крамера незаменимо и используется весьма продуктивно.

2. Если и хотя бы один определитель , то система несовместна. Если , то возможны два случая: либо система несовместна, либо имеет бесконечно много решений.

Пример 5.1. Решить систему линейных уравнений с помощью правила Крамера

Решение. Составим матрицу системы . Вычислим ее определитель

Так как определитель отличен от нуля, система имеет единственное решение (см. теорему 5.1). Находим определители и неизвестные

Условие совместности системы линейных уравнений

Рассмотрим систему (5.3) линейных уравнений с неизвестными. Составим блочную матрицу, приписав к матрице справа столбец свободных членов. Получим расширенную матрицу системы :

Эта матрица содержит всю информацию о системе уравнений, за исключением обозначений неизвестных.

Теорема 5.2 Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы: .

Необходимость следует из равенства (5.5) и следствия 1 теоремы 3.3. Если система имеет решение, то столбец свободных членов есть линейная комбинация столбцов матрицы системы. Поэтому при вычеркивании столбца Ь из расширенной матрицы ее ранг не изменяется. Следовательно, .

Для доказательства достаточности нужно использовать теорему о базисном миноре. Из равенства следует, что базисный минор матрицы является базисным минором расширенной матрицы . Поэтому столбец является линейной комбинацией столбцов базисного минора матрицы , а, значит, и всех столбцов матрицы . Следовательно, существуют числа , удовлетворяющие условию (5.5), т.е. система совместна.

Замечание 5.2. Теорема Кронекера-Капелли дает лишь критерий существования решения системы, но не указывает способа отыскания этого решения.

Пример 5.2. Определить, имеет ли система уравнений решения

Решение. Составим матрицу системы и расширенную матрицу системы

Ранг матрицы равен 2, так как она имеет не равные нулю миноры второго порядка и третья строка этой матрицы равна сумме первых двух строк. Следовательно, третью строку можно вычеркнуть, при этом ранг матрицы не изменится. Ранг расширенной матрицы равен трем, так как она имеет не равный нулю минор третьего порядка, например, минор, составленный из первого, второго и последнего столбцов расширенной матрицы

Следовательно, . Поэтому система несовместна (не имеет решений).