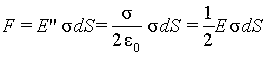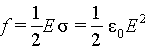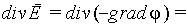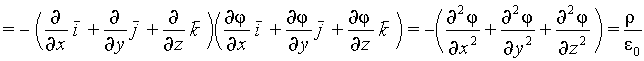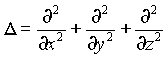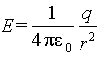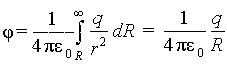Уравнение Пуассона и математическая постановка задач электростатики
Вы будете перенаправлены на Автор24
Решение уравнения Пуассона
В достаточно большом количестве случаев наиболее удобным методом поиска напряженности поля является решение дифференциального уравнения для потенциала. Получим его, используя в качестве основы теорему Остроградского — Гаусса в дифференциальной форме:
где $\rho $ — плотность распределения заряда, $<\varepsilon >_0$ — электрическая постоянная, $div\overrightarrow
Подставим (2) в (1), получим:
Учитываем, что $divgrad\varphi =<\nabla >^2\varphi =\frac<<\partial >^2\varphi ><\partial x^2>+\frac<<\partial >^2\varphi ><\partial y^2>+\frac<<\partial >^2\varphi ><\partial z^2>$, где $\triangle =<\nabla >^2$- оператор Лапласа, тогда равенство (3) запишем как:
Уравнение (4) называется уравнением Пуассона (для вакуума) в системе СИ. Если заряды отсутствуют, то уравнение (4) преобразуется в уравнение Лапласа:
После того, как найден потенциал из уравнения Пуассона, обычно вычисляется напряженность по формуле (2). Решения уравнения Пуассона должны удовлетворять таким требованиям:
- Потенциал должен быть непрерывной функцией.
- Потенциал должен быть конечной функцией.
- Производные от потенциала как функции по координатам должны быть конечными.
Если заряды сосредоточены в объеме V, то решением уравнения (4) будет выражение для потенциала вида:
Итак, общая задача электростатики сводится к нахождению решения дифференциального уравнения (уравнения Пуассона), которое удовлетворяет выше перечисленным требованиям. Нахождение решения — задача весьма сложная. Теоретические решения известны для небольшого количества частных случаев. Если удалось подобрать функцию $\varphi $, которая удовлетворяет всем условиям задачи, то она единственная.
Готовые работы на аналогичную тему
Не всегда есть необходимости задавать заряды или потенциалы во всем пространстве. Например, если необходимо найти электрическое поле в полости, которая окружена проводящей оболочкой, то можно найти поле только для тел внутри самой полости.
Каждое решение уравнения Пуассона в ограниченной области однозначно определяется краевыми условиями, которые накладывают на поведение решения. На границе перехода из одной среды в другую выполняются граничные условия:
где $\sigma $- поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 1 в 2, $\tau -\ $единичный вектор, касательный к границе.
Данные уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной составляющей вектора напряженностей электрического поля при переходе через любую заряженную поверхность не зависимо от формы этой поверхности и наличия и отсутствия зарядов вне ее.
Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Уравнение Пуассона может быть записано не только в декартовых координатах, но также в сферических и цилиндрических, полярных.
В сферических координатах ($r,\theta ,\vartheta)$ уравнение Пуассона имеет следующий вид:
В полярных координатах ($r,\theta )$ система координат уравнение имеет вид:
В цилиндрических координатах ($r,\vartheta,z)$ уравнение имеет вид:
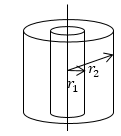
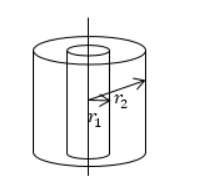
Задание: Найдите поле между двумя коаксиальными цилиндрами с радиусами $r_1$ и $r_2$, разность потенциалов между которыми равна $\triangle U=<\varphi >_1-<\varphi >_2.$
Запишем уравнение Лапласа в цилиндрических координатах с учетом аксиальной симметрии:
Оно имеет решение $\varphi =-Aln(r)$+B. Выберем нулевой потенциал на наружном цилиндре, найдем, получим:
$\varphi \left(r_2\right)=0=-Alnr_2+B,$ следовательно
Ответ: Поле между двумя коаксиальными цилиндрами задается функцией $\varphi (r)=-\frac<\triangle U><
Задание: Найти, используя уравнение Пуассона потенциал поля, которое создает бесконечно длинный круглый цилиндр радиуса R с объемной плотностью заряда $\rho $.
Ось Z направим по оси цилиндра. Так как цилиндрическое распределение заряда аксиально симметрично, то потенциал обладает той же симметрией, то есть он является функцией $\varphi \left(r\right),\ $где r — расстояние от оси цилиндра. Поэтому используем цилиндрическую систему координат. Запишем уравнение Пуассона в ней с учетом симметрии:
где $C_1$,$\
Так как поверхностных зарядов нет, то напряженность электрического поля на поверхности шара непрерывна, то есть непрерывна производная от потенциала при r=R. И непрерывен сам потенциал. Эти условия дают два алгебраических уравнения для того, чтобы найти постоянные $C_2$,$\
Следовательно, получаем выражения для потенциалов:
\[<\varphi >_1\left(r\right)=-\frac<1><4>\frac<\rho ><<\varepsilon >_0> r ^ 2 \left(0 Ответ: Потенциал поля равен: $$ \varphi_1 \left(r \right)=-\frac<1><4>\frac<\rho > <\varepsilon_0>r^2 \left (0
Уравнение Пуассона и математическая постановка задач электростатики
Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:
где ρ является плотностью распределения заряда, ε 0 — электрической постоянной, d i v E → = ∇ → E → = ∂ E x ∂ x + ∂ E y ∂ y + ∂ E z ∂ z — дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.
Произведем подстановку ( 2 ) в ( 1 ) :
Учитывая, что d i v g r a d φ = ∇ 2 φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 + ∂ 2 φ ∂ z 2 , где ∆ = ∇ 2 — это оператор Лапласа, равенство ( 3 ) принимает вид:
Выражение ( 4 ) получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:
После нахождения потенциала переходим к вычислению напряженности, используя ( 2 ) . Решения уравнения Пуассона должны удовлетворять требованиям:
- значение потенциала как непрерывная функция;
- потенциал должен быть конечной функцией;
- производные потенциала как функции по координатам должны быть конечными.
При наличии сосредоточенных зарядов в объеме V , решение уравнения ( 4 ) будет выражаться для потенциала вида:
Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию φ , удовлетворяющую условиям, то она является единственным решением.
В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.
Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:
E 2 n — E 1 n = 4 π σ , или ∂ φ 1 ∂ n — ∂ φ 2 ∂ n = 0 .
где σ — это поверхностная полость свободных зарядов, n – единичный вектор нормали к границе раздела, проведенный из среды 1 в 2 , τ — единичный вектор, касательный к границе.
Эти уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной вектора напряженностей электрического поля при переходе через любую заряженную поверхность независимо от ее формы и наличия или отсутствия зарядов вне ее.
Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Запись уравнения может быть как при помощи декартовых координат, также и сферических, цилиндрических, полярных.
При наличии сферических r , θ , υ уравнение Пуассона запишется как:
1 r 2 · ∂ ∂ r r 2 ∂ φ ∂ r + 1 r 2 sin θ ∂ θ sin θ · ∂ φ ∂ θ + ∂ 2 φ r 2 sin 2 θ ∂ φ 2 = — 1 ε 0 ρ .
В полярных r , θ :
1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ r 2 ∂ θ 2 = — 1 ε 0 ρ .
В цилиндрических r , υ , z :
1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ ∂ z 2 + ∂ 2 φ r 2 ∂ υ 2 = — 1 ε 0 ρ .
Примеры решения задач
Найти поле между коаксиальными цилиндрами с радиусами r 1 и r 2 и с имеющейся разностью потенциалов ∆ U = φ 1 — φ 2 .
Решение
Необходимо зафиксировать уравнение Лапласа с цилиндрическими координатами, учитывая аксиальную симметрию:
1 r · ∂ ∂ r r ∂ φ ∂ r = 0 .
Решение имеет вид φ = — A ln ( r ) + B . Для этого следует выбрать нулевой потенциал на нужном цилиндре, тогда:
φ ( r 2 ) = 0 = — A ln r 2 + B , следовательно
φ ( r 1 ) = ∆ U = — A ln r 1 + B , получим:
A = ∆ U ln r 2 r 1 .
φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .
Ответ: поле с двумя коаксиальными цилиндрами может быть задано при помощи функции φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .
Найти потенциал поля, которое создает бесконечно круглый цилиндр с радиусом R и объемной плотностью заряда ρ . Использовать уравнение Пуассона.
Решение
Необходимо направить ось Z по оси цилиндра. Видно, что цилиндрическое распределение заряда аксиально симметрично, потенциал имеет такую же симметрию, иначе говоря, считается функцией φ ( r ) с r , являющимся расстоянием от оси цилиндра. Для решения используется цилиндрическая система координат. Уравнение Пуассона в ней запишется как:
φ 2 = C 2 ln r + C ‘ 2 .
C 1 , C ‘ 1 , C 2 , C ‘ 2 — это постоянные интегрирования. Имеем, что потенциал во всех точках должен быть конечным, а l i m r → 0 ln r = ∞ . Отсюда следует, что C 1 = 0 . Далее необходимо пронормировать потенциал, задействовав условие φ 1 ( 0 ) = 0 . Получим C ‘ 1 = 0 .
Поверхностные заряды отсутствуют, поэтому напряженность электрического поля на поверхности шара является непрерывной. Следовательно, что и производная от потенциала также непрерывна при r = R , как и сам потенциал. Исходя из условий, можно найти C 2 , C ‘ 2 :
C 2 ln R + C ‘ 2 = — 1 4 ρ ε 0 R 2 .
C 2 R = — 1 2 ρ ε 0 R .
Значит, полученные выражения записываются как:
Ответ: потенциал поля равняется:
Общая задача электростатики уравнение пуассона
Для определенности будем рассматривать только твердые тела. Проводник электричества — это тело, в котором много «свободных» электронов. Электроны могут двигаться в веществе свободно, но не могут покидать поверхности. В условиях электростатики электроны движутся только до тех пор пока за малые доли секунды не расположатся так, что повсюду внутри проводника создастся нулевое электрическое поле. Такое поведение электронов легко понять, если принять во внимание, что пока поле не нулевое, на электроны действует сила, приводящая к их перемещению.
Рассмотрим внутренность проводника. Так как E=0, то (см. 1.18) и grad φ =0, т.е. φ =const. Любой проводник — это эквипотенциальная область, а его поверхность эквипотенциальна. Поскольку E=0 всюду в проводнике, то и divE=0, а так как согласно теореме Гаусса в дифференциальной форме divE= ρ/ε o, то и ρ =0, т.е. плотность заряда во внутренней части проводника обращается в нуль. Любой заряд, попавший в проводник, собирается на его поверхности, располагаясь так, чтобы выполнялись условия равновесия заряда на проводнике: внутри проводника E=0, а снаружи, вблизи поверхности, E=En. Таким образом напряженность E по обе стороны поверхности имеет различные значения, и, стало быть, на самой поверхности остается неопределенной.
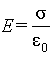 | (4.1) |
| Таким образом напряженность поля в некоторой точке вблизи поверхности вне проводника выражается через поверхностную плотность заряда s вблизи этой точки. |
При этом надо иметь в виду, что s в районе выбранной точки определяется равновесным распределением заряда по всему проводнику, и напряженность поля вблизи данной точки определяется всем зарядом проводника. Это особенно наглядно видно при определении силы, действующей на поверхностные заряды.
В случае одного единственного уединенного проводника все электрические силы сводятся к взаимному отталкиванию зарядов. Так как заряды не могут покинуть проводник, то к его поверхности будут приложены силы, стремящиеся ее растянуть.
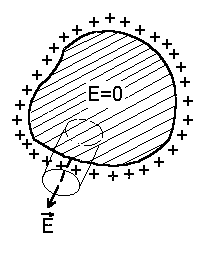
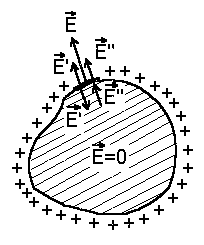 | Рассмотрим элемент поверхности проводника dS. Поле E’ заряда, находящегося на dS, направлено в обе стороны от площадки. Весь остальной заряд на проводнике располагается таким образом, чтобы созданное им вблизи dS поле E» компенсировало поле E’ внутри проводника (см. рис. 4.2). Согласно принципу суперпозиции E=E’+E». Таким образом внутри проводника E=E‘ — E»=0, откуда E‘=E». В двух смежных точках с внешней и внутренней стороны dS поле E» одинаково. Так как с внешней стороны модуль напряженности поля E=E‘+E»= σ / ε o (см. 4.1), то E‘=E»= σ / 2ε o. Сила, действующая на элемент поверхности dS, равна произведению заряда на этом элементе на напряженность поля, создаваемую всеми зарядами проводника кроме тех, которые находятся на dS, т.е. F= σ dSE». Тогда сила
|
а на единицу площади поверхности проводника приходится сила
Направление этой силы совпадает с направлением внешней нормали к элементу поверхности проводника.
Уравнение Пуассона
Подставляя (1.18) в (2.17), найдем общее дифференциальное уравнение для потенциала.
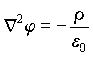 , , | (4.2а) |
что может быть записано, также, как
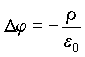 , , | (4.2б) |
где D — оператор Лапласа, имеющий в декартовой системе координат следующий вид:
Уравнение (4.2а-б), носящее имя Пуассона, можно рассматривать как дифференциальное выражение, соответствующее интегралу (1.16) с помощью которого потенциал в точке вычисляется как сумма вкладов от всех источников заряда, распределенных в пространстве с плотностью r .
Если между проводниками нет зарядов, то уравнение Пуассона переходит в следующее уравнение, которое носит название уравнения Лапласа:
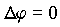 | (4.3) |
Основная задача электростатики
Задача заключается в определении функции φ (x,y,z), которая удовлетворяет уравнению (4.3), а также определенным граничным условиям. Граничные условия — это значения φ (x,y,z) во всех точках поверхности, охватывающей область, в которой определена функция φ. При этом на поверхности, удаленной в бесконечность, потенциал φ принимается равным нулю. На проводящих поверхностях могут быть заданы потенциалы каждого проводника или величина полного заряда на каждом проводнике. Объемные заряды предполагаются отсутствующими, ибо заряды проводников сосредоточены на их поверхности.
Основная задача электростатики может быть сформулирована следующим образом.
Дано: расположение и форма всех проводников, а также либо потенциал каждого проводника, либо общий заряд каждого проводника.
Найти: поле этих проводников и распределение зарядов по их поверхности.
В теории доказывается, что существует только одна функция φ (x,y,z), удовлетворяющая уравнению Лапласа и принимающая на границах заданные значения, т.е., что решение задачи единственно.
Однозначность решения позволяет заключить, что как угодно найденная любая функция φ (x,y,z), являющаяся решением уравнения (4.3) и удовлетворяющая граничным условиям есть единственное и потому истинное решение задачи.
Метод изображений
Метод изображений — это способ решения основной задачи электростатики, основанный на подмене исходной конфигурации проводников некоторым другим распределением зарядов, потенциал которого на поверхности проводников и в бесконечности совпадает с граничными условиями исходной задачи. Новая задача, разумеется, должна иметь простое решение. Поскольку решение при данных граничных условиях единственно, то оно является и решением исходной задачи.
Пример: Точечный заряд q находится на расстоянии d от бесконечного проводника, занимающего левое полупространство. Определить поле в правом полупространстве.
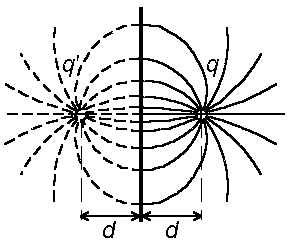 | Общий заряд точечного проводника задан. Потенциал проводника, уходящего в бесконечность, естественно принять за нуль. Этими условиями решение определяется однозначно. Чтобы найти это решение, предположим, что на продолжении перпендикуляра, опущенного из заряда на поверхность проводника, находится на расстоянии d заряд q‘ = — q (см. рис. 4.3) и затем мысленно уберем сам проводник . Тогда плоскость, совпадавшая ранее с поверхностью проводника, будет обладать требуемым нулевым потенциалом, ибо все точки этой плоскости будут равно отстоять от равных по величине и противоположных по знаку зарядов. |
Стало быть, поле совокупности этих зарядов в правом полупространстве удовлетворяет условиям задачи, из чего на основании того, что решение единственно следует, что поле это в правом полупространстве тождественно искомому полю заряда q и зарядов, индуцированных им на поверхности бесконечного проводника. Таким образом задача сведена к простой задаче двух зарядов. Следует заметить, что внутри проводника E=0, и поле не совпадает с полем заряда и проводника.
Поле в полости
Покажем, что в пустой полости внутри проводника электрическое поле равно нулю. Функция φ (x,y,z) должна удовлетворять уравнению Лапласа всюду внутри полости. Вся граница полости (или замкнутой проводящей оболочки) является эквипотенциальной, т.е. на ней φ = φ о. Одним из решений уравнения (4.3) является решение φ (x,y,z)=const во всей области определения функции, т.е. во всем объеме полости. Выберем в качестве этой константы φ о. Тогда полученное решение удовлетворяет граничным условиям, причем это единственное решение. Для напряженности поля получим E= —grad φ о= 0. Таким образом в электростатике никаким распределением зарядов снаружи замкнутой проводящей оболочки невозможно создать поле внутри нее.
Емкость
Электроемкость или просто емкость — это мера способности проводника накапливать электрический заряд. Потенциал уединенного проводника произвольной формы пропорционален его заряду. Пропорциональность между зарядом, сообщенном проводнику, и его потенциалом возникает из-за принципа суперпозиции. Пусть известно решение уравнения Лапласа во всем пространстве вокруг проводника, при заданном заряде проводника в качестве граничных условий. Если согласно принципу суперпозиции наложить на это решение другое такое же решение для тех же граничных условий, то заряды и поля удвоятся и работа по переносу заряда из бесконечности в данную точку поля тоже удвоится. По этой причине потенциал проводника пропорционален его заряду. Численно емкость равна заряду q, который необходимо сообщить уединенному телу для изменения его потенциала φ на единицу, и определяется соотношением C=q/ φ . За единицу емкости принимают емкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл. Эта единица емкости называется Фарадом (Ф).
Вычислим емкость проводящего шара радиуса R в вакууме. Заряд проводника сосредоточен на его поверхности. Поле заряженной сферы легко находится с помощью теоремы Гаусса:
Потенциал сферы равен
Тогда емкость равна C=q/ φ = 4 π εo R.
http://zaochnik.com/spravochnik/fizika/elektricheskoe-pole/uravnenie-puassona/
http://iatephysics.narod.ru/lecture4/lecture4.htm