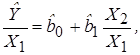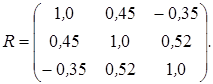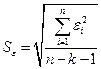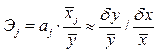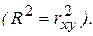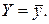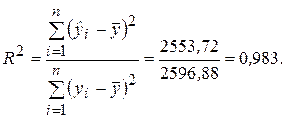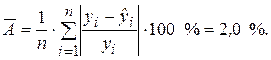Общее качество уравнения регрессии оценивается с помощью

Проверка общего качества уравнения

Множественной регрессии

Для проверки общего качества уравнения регрессии обычно используется коэффициент детерминации R 2 , который характеризует долю дисперсии зависимой переменной Y, объясняемую регрессионной моделью, и определяется по формуле:

(3.27)

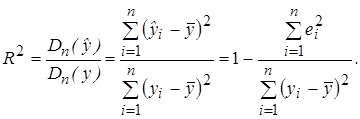
Свойства коэффициента R 2 подробно рассмотрены в разделе 2.4.

Для множественной регрессии коэффициент детерминации (или множественный коэффициент детерминации) является неубывающей функцией числа объясняющих переменных, т. е. добавление новой объясняющей переменной (фактора-аргумента Х) в модель никогда не уменьшает значение R 2 . Действительно, каждая новая объясняющая переменная может лишь дополнить информацию, объясняющую поведение зависимой переменной. В целом это уменьшает неопределенность в поведении исследуемой величины Y. Однако увеличение R 2 при добавлении новых переменных далеко не всегда приводит к улучшению качества регрессионной модели, так как эти переменные могут не оказывать существенного влияния на результативный признак. Поэтому, наряду с коэффициентом R 2 , для анализа используется скорректированный коэффициент детерминации 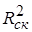, определяемый соотношением:

(3.28)

или с учетом (3.27)

. (3.29)

Можно заметить, что знаменатель в (3.29) является несмещенной оценкой общей дисперсии зависимой переменной Y, а числитель – несмещенной оценкой остаточной дисперсии (дисперсии случайных отклонений).

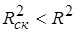
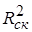
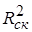
Скорректированный коэффициент детерминации устраняет (корректирует) неоправданный эффект, связанный с ростом R 2 при увеличении числа объясняющих переменных. Из (3.28) следует, что при m > 1 Можно показать, что увеличивается при добавлении новой объясняющей переменной только тогда, когда t-статистика для этой переменной по модулю больше единицы, т. е. когда ее коэффициент регрессии (параметр модели) считается относительно значимым. Таким образом, в определенной степени использование скорректированного коэффициента детерминации более предпочтительно для сравнения регрессионных моделей при изменении количества объясняющих переменных (регрессоров). Добавление в модель новых регрессоров может осуществляться до тех пор, пока растет .

В компьютерных пакетах приводятся данные как по R 2 , так и по 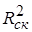, которые используются на практике для оценки суммарной меры общего качества построенной регрессионной модели.

В общем случае качество модели считается удовлетворительным, если R 2 > 0,5. Однако не следует рассматривать коэффициент детерминации как абсолютный показатель качества модели. Можно привести ряд примеров, когда неправильно специфицированные модели имели сравнительно высокие коэффициенты детерминации. Поэтому коэффициент детерминации в современной эконометрике следует рассматривать лишь как один из показателей, который необходим для анализа строящейся модели.

Анализ общей (совокупной) статистической значимости уравнения множественной регрессии осуществляется на основе проверки основной гипотезы об одновременном равенстве нулю всех коэффициентов при объясняющих переменных:

Если данная гипотеза не отклоняется, то естественно считать уравнение модели статистически незначимым, т. е. не выражающим существенную линейную связь между Y и Х₁, Х₂, …, Х_m.

Напомним (см. раздел 2.4.3), что общая дисперсия зависимой переменной D_n(y) может быть представлена в виде суммы двух составляющих:

где D_n(y) – соответственно, дисперсия, объясняемая уравнением множественной регрессии, и необъясняемая (остаточная) дисперсия, характеризующая влияние неучтенных факторов.

Исходя из этого проводится дисперсионный анализ для проверки гипотезы Н₀ (F-тест).

Строится проверочная F-статистика:

(3.30)

где – объясняемая дисперсия (в уравнении множественной регрессии вместе со свободным членом оценивается k = m + 1 параметров); – остаточная дисперсия. При выполнении предпосылок МНК построенная статистика имеет распределение Фишера с числами степеней свободы v₁ = m, v₂ = n — m — 1. Поэтому гипотеза Н₀ отклоняется, если при заданном уровне значимости a значение F_набл, рассчитанное по формуле (3.30), больше, чем критическое значение F_кр = F_{a; m; n — 1 — m} (F_набл > F_кр), и делается вывод о статистической значимости уравнения множественной регрессии. В противном случае (F_набл > F_кр) нет оснований для отклонения Н₀. Это означает, что объясняемая построенной моделью дисперсия соизмерима с дисперсией, вызванной неучтенными факторами, а следовательно, общее качество модели невысоко.

Если рассчитан коэффициент детерминации R 2 , то критерий значимости уравнения регрессии (3.30) может быть представлен в следующем виде:

(3.31)

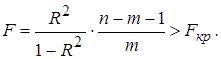
Критерий (3.31) обычно используется на практике для тестирования гипотезы о статистической значимости коэффициента детерминации (Н₀ : R 2 = 0; Н₁ : R 2 > 0) которая эквивалентна гипотезе об общей статистической значимости уравнения множественной регрессии.

Отметим, что в отличие от парной регрессии, где t-тест и F-тест равносильны, в случае множественной регрессии коэффициент R 2 приобретает самостоятельную значимость.

Пример 3.2. Оценим статистическую значимость построенной модели.

Пусть при оценке регрессии с тремя объясняющими переменными ( по 30 наблюдениям получено значение коэффициента детерминации R 2 = 0,7. Тогда, наблюдаемое значение F-ста­тистики . По таблице критических точек распределения Фишера найдем F_{0,05; 3; 26} = 2,98 при заданном уровне значимости a = 0,05. Поскольку F_набл = 20,2 > F_кр = 2,98, то нулевая гипотеза отклоняется, т. е. отвергается предположение о незначимости линейной связи.

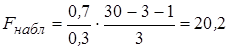
Мультиколлинеарность

Весьма нежелательным эффектом, который может проявляться при построении моделей множественной регрессии и искажать статистическую информацию, полученную по модели, является мультиколлинеарность [1,28,33]– линейная взаимосвязь двух или нескольких объясняющих переменных. Различают функциональную и корреляционную формы мультиколлинеарности.

При функциональной форме мультиколлинеарности по крайней мере два регрессора связаны между собой линейной функциональной зависимостью. В этом случае определитель матрицы Х Т Х равен нулю в силу присутствия линейно зависимых вектор-столбцов (нарушается предпосылка 5 МНК), что приводит к невозможности решения соответствующий системы уравнений и получения оценок параметров регрессионной модели.

Однако в эконометрических исследованиях мультиколлинеарность чаще всего проявляется в более сложной корреляционной форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Ниже рассмотрены некоторые способы обнаружения, а также уменьшения и устранения мультиколлинеарности.

Один из таких способов заключается в исследовании матрицы Х Т Х. Если ее определитель близок к нулю, то это может свидетельствовать о наличии мультиколлинеарности. В этом случае наблюдаются значительные стандартные ошибки коэффициентов регрессии и их статистическая незначимость по t-критерию, хотя в целом регрессионная модель может оказаться значимой по F-тесту.

Другой подход состоит в анализе матрицы парных коэффициентов корреляции между объясняющими переменными (факторами). Если бы факторы не коррелировали между собой, то корреляционная матрица R была бы единичной матрицей, поскольку все недиагональные элементы (х_i ¹ x_j) равны нулю. Определитель такой матрицы равен единице [Тимофеев, 2013]. Например, для модели, включающей три объясняющих переменных , в этом случае имеем:

. (3.32)

Если же, наоборот, между факторами-аргументами существует полная линейная зависимость и все коэффициенты корреляции равны 1 (|r_ij| = 1), то определитель матрицы межфакторной корреляции равен нулю

. (3.33)

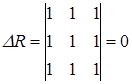
Таким образом, чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность объясняющих переменных и ненадежнее оценки множественной регрессии, полученные с использованием МНК.

Если в модели больше двух объясняющих переменных, то для обнаружения мультиколлинеарности полезно находить частные коэффициенты корреляции, поскольку парные коэффициенты корреляции определяют силу линейной зависимости между двумя факторами без учета влияния на них других объясняющих переменных. Например, между двумя экономическими переменными может наблюдаться высокий положительный коэффициент корреляции совсем не потому, что одна из них стимулирует изменение другой, а вследствие того, что обе эти переменные изменяются в одном направлении под влиянием других факторов, присутствующих в модели. Поэтому возникает необходимость оценки действительной тесноты (силы) линейной связи между двумя факторами, очищенной от влияния других переменных. Параметр, определяющий степень корреляции между двумя факторами Х_i и X_j при исключении влияния остальных переменных называется частным коэффициентом корреляции.

Например, в случае модели с тремя объясняющими переменными Х₁, Х₂, Х₃ частный коэффициент корреляции между Х₁ и Х₂ рассчитывается по формуле:

(3.34)

Частный коэффициент корреляции может существенно отличаться от «обычного» парного коэффициента корреляции r₁₂. Пусть, например, r₁₂ = 0,5; r₁₃ = 0,5; r₂₃ = -0,5. Тогда частный коэффициент корреляции r_12.3 = 1 (3.34), т. е. при относительно невысоком коэффициенте корреляции r₁₂ частный коэффициент корреляции указывает на высокую зависимость (коллинеарность) между переменными Х_i и X_j.

Таким образом, для обоснованного вывода о корреляции между объясняющими переменными множественной регрессии необходимо рассчитывать частные коэффициенты корреляции.

Частный коэффициент корреляции r_{ij.1, 2, …, m}, как и парный коэффициент r_ij, может принимать значения от -1 до 1. Присутствие в модели пар переменных, имеющих высокие коэффициенты частной корреляции (обычно больше 0,8), свидетельствует о наличии мультиколлинеарности.

Для устранения или уменьшения мультиколлинеарности используется ряд методов, простейшим из которых является исключение из модели одной или нескольких коррелированных переменных. Обычно решение об исключении какой-либо переменной принимается на основании экономических соображений. Следует заметить, что при удалении из анализа объясняющей переменной можно допустить ошибку спецификации. Например, при изучении спроса на некоторый товар в качестве объясняющих переменных целесообразно использовать цену данного товара и цены товаров-заменителей, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, вероятнее всего, допустим ошибку спецификации. Вследствие этого можно получить смещенные оценки и сделать ненадежные выводы.

Иногда для уменьшения мультиколлинеарности достаточно (если это возможно) увеличить объем выборки. Например, при использовании ежегодных показателей можно перейти к поквартальным данным. Увеличение количества данных сокращает дисперсии коэффициентов регрессионной модели и тем самым увеличивает их статистическую значимость.

В ряде случаев минимизировать либо вообще устранить мультиколлинеарность можно с помощью преобразования переменных, в результате которого осуществляется переход к новым переменным, представляющим собой линейные или относительные комбинации исходных [11].

Например, построенная регрессионная модель имеет вид:

(3.35)

причем Х₁ и Х₂ – коррелированные переменные. В этом случае целесообразно оценивать регрессионные уравнения относительных величин:

.

Следует ожидать, что в моделях, построенных аналогично (3.36), эффект мультиколлинеарности не будет проявляться.

Существуют также другие, более теоретически разработанные способы обнаружения и подавления мультиколлинеарности, подробное описание которых выходит за рамки данной книги. Одним из таких методов является факторный анализ. Сущностью факторного анализа является процедура вращения факторов, т.е. перераспределение дисперсии по определённому методу с целью получения максимально простой и наглядной структуры факторов (выделение главных компонент) [23,35]. В результате проведения факторного анализа можно соответствующим образом сократить число переменных, тем самым избежать проявления мультиколлинеарности. При этом в один фактор объединяются сильно коррелирующие между собой переменные, что позволяет проводить регрессионный анализ на главных компонентах.

Факторный анализ играет большую самостоятельную роль в экономике и, прежде всего, разработан для поиска ненаблюдаемых, латентных переменных (факторов), имеющих определённый социально-экономический смысл [23].

Следует заметить, что если основная задача, решаемая с помощью эконометрической модели – прогнозирование поведения реального экономического объекта, то при общем удовлетворительном качестве модели проявление мультиколлинеарности не является слишком серьезной проблемой, требующей приложения больших усилий по ее выявлению и устранению, т. к. в данном случае наличие мультиколлинеарности не будет существенно сказываться на прогнозных качествах модели. Таким образом, вопрос о том – следует ли серьезно заниматься проблемой мультиколлинеарности или «смириться» с ее проявлением – решается исходя из целей и задач эконометрического анализа.

Вопросы и упражнения для самопроверки

1. Какова общая структура модели множественной линейной регрессии?

2. Опишите алгоритм определения коэффициентов множественной линейной регрессии (параметров модели) по МНК в матричной форме.

3. Как определяется статистическая значимость коэффициентов регрессии?

4. В чем суть скорректированного коэффициента детерминации и его отличие от обычного R 2 ?

5. Как используется F-статистика во множественном регрессионном анализе?

6. Вычислите величину стандартной ошибки регрессионной модели со свободным членом и без него, если 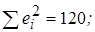n = 30; m = 3.

7. На основе n = 30 наблюдений оценена модель с тремя объясняющими переменными. Получены следующие результаты:

Стандартные ошибки (2,5) (1,6) (2,8) (0,07)

Проведите необходимые расчеты и занесите данные в скобки. Сделайте выводы о существенности коэффициентов регрессии на уровне значимости a =0,05.

8. Имеются данные о ставках месячных доходов по трем акциям за шестимесячный период:

Есть основания предполагать, что доходы по акции С(Y) зависят от доходов по акциям А(X₁) и В(X₂). Необходимо:

а) составить уравнение регрессии Y по X₁ и X₂ с использованием МНК (указание: для удобства вычислений сумм первых степеней, квадратов и попарных произведений переменных составьте вспомогательную таблицу);

б) найти множественный коэффициент детерминации R 2 и оценить общее качество построенной модели;

в) проверить значимость полученного уравнения регрессионной модели на уровне a = 0,05.

9. Объясните суть матрицы ковариаций случайных отклонений.

10. Дайте определение и объясните смысл мультиколлинеарности факторов-аргументов.

11. Каковы основные последствия мультиколлинеарности?

12. Какие вы знаете способы обнаружения мультиколлинеарности?

13. Как оценивается степень коррелированности между двумя объясняющими переменными?

14. Перечислите основные методы устранения мультиколлинеарности.

15. В чем заключается сущность факторного анализа?

16. Как определяются парный и частный коэффициенты корреляции для независимых переменных.

17. Для модели с тремя независимыми переменными X₁, X₂, X₃ построенной по n = 50 наблюдениям, определена следующая корреляционная матрица:

б) определить, имеет ли место мультиколлинеарность для уравнения регрессии.

Показатели качества регрессии

Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия) модели регрессии наблю­даемым данным проводится на основе анализа остатков — .

Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности, почти независимые) одинаково распределенные случайные величины.

Качество модели регрессии оценивается по следующим направлениям:

проверка качества всего уравнения регрессии;

проверка значимости всего уравнения регрессии;

проверка статистической значимости коэффициентов уравнения регрессии;

проверка выполнения предпосылок МНК.

При анализе качества модели регрессии, в первую очередь, используется коэффициент детерминации, который определяется следующим образом:

где 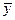— среднее значение зависимой переменной,

— предсказанное (расчетное) значение зависимой переменной.

Коэффициент детерминации показывает долю вариации результативного признака, находя­щегося под воздействием изучаемых факторов, т. е. определяет, ка­кая доля вариации признака Y учтена в модели и обусловлена влия­нием на него факторов.

Чем ближе 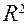к 1, тем выше качество модели.

Для оценки качества регрессионных моделей целесообразно также ис­пользовать коэффициент множественной корреляции (индекс корреляции) R

R = =

Данный коэффициент является универсальным, так как он отра­жает тесноту связи и точность модели, а также может использовать­ся при любой форме связи переменных.

Важным моментом является проверка значимости построенного уравнения в целом и отдельных параметров.

Оценить значимость уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и Х, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y

Оценка значимости уравнения регрессии производится для того, чтобы узнать, пригодно уравнение регрессии для практического использования (например, для прогноза) или нет.

Для проверки значимости модели регрессии используется F-критерий Фишера. Если расчетное значение с n1= k и n2 = (n — k — 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.

В качестве меры точности применяют несмещенную оценку дис­персии остаточной компоненты, которая представляет собой отно­шение суммы квадратов уровней остаточной компоненты к величи­не (n- k -1), где k – количество факторов, включенных в модель. Квадратный корень из этой величины ( ) называется стандартной ошибкой:

значимость отдельных коэффициентов регрессии проверяется по t-статистике пу­тем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):

,

где Saj — это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии aj. Величина Saj представляет собой квадратный корень из произ­ведения несмещенной оценки дисперсии и j -го диагонального эле­мента матрицы, обратной матрице системы нормальных уравнений.

где — диагональный элемент матрицы .

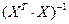
Если расчетное значение t-критерия с (n — k — 1) степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует ис­ключить из модели (при этом ее качество не ухудшится).

Проверка выполнения предпосылок МНК.

Рассмотрим выполнение предпосылки гомоскедастичности, или равноизменчивости случайной составляющей (возмущения).

Невыполнение этой предпосылки, т.е. нарушение условия гомоскедастичности возмущений означает, что дисперсия возмущения зависит от значений факторов. Такие регрессионные модели называются моделями с гетероскедастичностью возмущений.

Обнаружение гетероскедастичности. Для обнаружения гетероскедастич­ности обычно используют тесты, в которых делаются различные предположения о зависимости между дисперсией случайного члена и объясняющей переменной: тест ранговой корреляции Спирмена, тест Голдфельда — Квандта, тест Глейзера, двусторонний критерий Фишера и другие [2].

При малом объеме выборки для оценки гетероскедастич­ности может использоваться метод Голдфельда — Квандта. Данный тест используется для проверки такого типа гетероскедастичности, когда дисперсия остатков воз­растает пропорционально квадрату фактора. При этом делается предположение, что, случайная составляющая 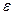распределена нормально.

Чтобы оценить на­рушение гомоскедастичности по тесту Голдфельда — Квандта необходимо выполнить следующие шаги.

Упорядочение п наблюдений по мере возрастания перемен­ной х.

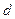
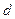
Исключение средних наблюдений ( должно быть примерно равно четверти общего количества наблюдений).

Разделение совокупности на две группы (соответственно с малыми и большими значениями фактора ) и определение по каждой из групп уравнений регрессии.

Определение остаточной суммы квадратов для первой регрессии и второй регрессии .

Вычисление отношений (или ). В числителе должна быть большая сумма квадратов.

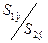
Полученное от­ношение имеет F распределение со степенями свободы k1=n1-k и k2=n-n1-k, (k– число оцениваемых параметров в уравнении регрессии).

Если , то гетероскедастичность имеет место.

Чем больше величина F превышает табличное значение F -критерия, тем более нарушена предпосылка о равенстве дисперсий остаточ­ных величин.

Оценка влияния отдельных факторов на зависимую переменную на основе модели (коэффициенты эластичности, b — коэффициенты).

Важную роль при оценке влияния факторов играют коэффициен­ты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени ко­леблемости. Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности Э(j) и бета-коэффициенты b(j).

Эластичность Y по отношению к Х(j) определяется как процентное изменение Y, отнесенное к соответствующему процентному изменению Х. В общем случае эластичности не постоянны, они различаются, если измерены для различных точек на линии регрессии. По умолчанию стандартные программы, оценивающие эластичность, вычисляют ее в точках средних значений:

Эластичность ненормирована и может изменяться от — до + . Важно, что она безразмерна, так что интерпретация эластичности =2.0 означает, что если изменится на 1%, то это приведет к изменению на 2%. Если =-0.5, то это означает, что увеличение на 1% приведет к уменьшению на 0.5%.

Высокий уровень эластичности означает сильное влияние независимой переменной на объясняемую переменную.

где Sxj — среднеквадратическое отклонение фактора j

где .

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора j на один процент. Однако он не учитывает степень колеблемости факторов.

Бета-коэффициент показывает, на какую часть величины средне­го квадратического отклонения Sy изменится зависи­мая переменная Y с изменением соответствующей независимой пере­менной Хj на величину своего среднеквадратического отклонения при фиксирован­ном на постоянном уровне значении остальных независимых пере­менных.

Указанные коэффициенты позволяют упорядочить факторы по степени влияния факторов на зависимую переменную.

Долю влияния фактора в суммарном влиянии всех факторов мож­но оценить по величине дельта — коэффициентов D (j):

где — коэффициент парной корреляции между фактором j (j = 1. m) и зависимой переменной.

В качестве основного литературного источника рекомендуется использовать [4], в качестве дополнительного – [2].

Анализ общего качества уравнения регрессии.

Коэффициент детерминации R 2

После проверки точности и статистической значимости каждого коэффициента регрессионной модели обычно проводится анализ общего качества уравнения модели, которое оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Другими словами, необходимо оценить, насколько широко рассеяны точки наблюдений по их совокупности относительно линии регрессии (линии модели). Поэтому представляется естественным вывод о том, что проверку общего качества регрессионной модели следует проводить на основе дисперсионного анализа, сравнивая дисперсии модельных и реальных значений исследуемой переменной Y.

Рассмотрим для определенного набора наблюдений n дисперсию D_n(y), которая характеризует разброс значений y_i вокруг среднего значения. Из дисперсионного анализа следует, что эту дисперсию можно разбить на две части: объясняемую уравнением регрессии и не объясняемую (т. е. связанную со случайными отклонениями e_i). Тогда выполняется следующее соотношение:

(2.27)

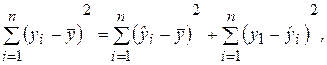
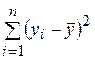
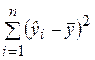
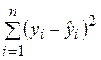
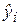
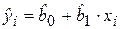
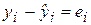
где – общая сумма квадратов отклонений зависимой переменной Y от среднего значения;

– сумма квадратов, объясняемая уравнением регрессии;

– необъясненная (остаточная) сумма квадратов. Напомним, что определяется как , а .

Разделив выражение (2.27) на его левую часть, получим формулу для оценки характеристики, которая обозначается как R 2 и называется коэффициентом детерминации:

(2.28)

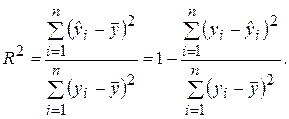
Коэффициент детерминации R 2 является мерой качества уравнения регрессионной модели и определяет долю дисперсии (разброса), объясняемую регрессией Y на Х, в общей дисперсии зависимой переменной Y.

Из проведенных рассуждений следует, что R 2 принимает значения между 0 и 1 (0 £ R 2 £ 1). Чем ближе R 2 к единице, тем теснее линейная связь между Х и Y (экспериментальные точки теснее примыкают к линии регрессии). Чем ближе R 2 к нулю, тем такая связь слабее. Если R 2 = 0, то дисперсия зависимой переменной полностью обусловлена воздействием неучтенных факторов и линия регрессии (модели) должна быть параллельна оси абсцисс (Y = ).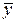

Например, если для построенной модели R 2 = 0,7, то согласно (2.28) можно утверждать, что поведение зависимой переменной (результативного признака) Y на 70 % объясняется влиянием фактора Х и на 30 % обусловлено влиянием неучтенных факторов. Доля влияния неучтенных факторов связана со случайными отклонениями e_i и определяется отношением 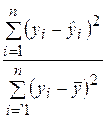, характеризующим долю разброса зависимой переменной, не объясняемую линейной регрессией Y на Х.

Естественно, что для исследуемого объекта наиболее качественной будет считаться модель с наибольшим значением коэффициента детерминации R 2 .

Заметим, что коэффициент детерминации имеет смысл рассматривать только при наличии параметра 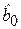(свободного члена) в уравнении регрессионной модели.

Таким образом, коэффициент детерминации R 2 определяет степень тесноты статистической связи между Y и Х. Но об этом же говорит выборочный коэффициент корреляции r_xy. Рассматривая эти характеристики, можно установить, что в случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции

Действительно, учитывая (2.13),

.

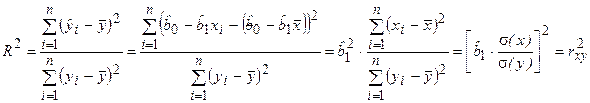
Естественно, возникает вопрос, какое значение R 2 можно считать удовлетворительным. Ответ на этот вопрос может быть неоднозначным, особенно в случае множественной регрессионной модели и зависит от объема выборки n и постановки задачи, вытекающей из предмодельного анализа.

Более точно проверить значимость уравнения регрессии, т. е. установить, соответствует ли построенная модель реальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной, позволяет F-тест, который проводится по схеме статистической проверки гипотез. Тестируется гипотеза Н₀ о статистической незначимости уравнения регрессии.

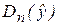
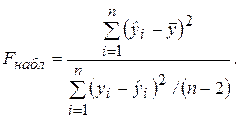
Рассмотрим «объясненную» и «необъясненную» дисперсии: и D_n(e). Отношение этих дисперсий, рассчитанное на одну степень свободы, имеет F-распределение (F-статистику), фактически наблюдаемое значение которой для парной регрессии определяется формулой

(2.29)

Учитывая смысл дисперсий 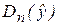и D_n(e), можно считать, что значение F_набл показывает, в какой мере уравнение регрессии лучше оценивает значение зависимой переменной по сравнению с

Согласно схеме статистической проверки гипотез, гипотеза Н₀ отклоняется, т. е. признается статистическая значимость и надежность уравнения регрессии на заданном уровне α, если F_набл превосходит критическое (табличное) значение F-статистики Фишера (F_набл > F_кр = F_α, 1, n — 2). Если F_набл 2 . В этом случае гипотеза Н₀ о статистической незначимости регрессионной модели заменяется эквивалентной гипотезой о статистической незначимости R 2 .

Для парной регрессионной модели способы проверки значимости коэффициента 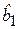с использованием t-критерия (t-тест) и уравнения регрессии (показателя тесноты связи R 2 ) с использованием F-критерия равносильны, поскольку эти критерии связаны соотношением F = t 2 .

Наряду с коэффициентом детерминации R 2 для оценки качества парной регрессионной модели можно использовать характеристику, называемую средней ошибкой аппроксимации :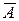

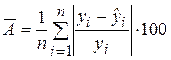
%. (2.31)

Средняя ошибка аппроксимации определяет среднее относительное отклонение расчетных данных (оцененных по уравнению модели) от фактических. 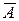является безразмерной величиной и обычно выражается в процентах. Принято считать, что качество модели считается удовлетворительным, если средняя ошибка аппроксимации не превышает 8-9 %.

Пример 2.3.Проверить общее качество и статистическую значимость уравнения регрессии для модели, построенной в примере 2.1.

Оценку качества построенной модели дают коэффициент детерминации R 2 и средняя ошибка аппроксимации .

Вычислим коэффициент детерминации, воспользовавшись данными табл. 2.1.

Величина коэффициента детерминации показывает, что поведение результативного признака (недельного потребления) Y на 98,3 % объясняется влиянием фактора Х (изменением недельного дохода), а остальные 1,7 % составляют долю необъясненной вариации, происходящей под действием прочих (неучтенных) факторов.

Расчет средней ошибки аппроксимации представлен в последнем столбце табл. 2.1.

Рассчитанные значения коэффициента детерминации и средней ошибки аппроксимации свидетельствуют о достаточно высоком общем качестве построенной модели.

Проверим статистическую значимость уравнения регрессионной модели с помощью F-теста. Расчетное (наблюдаемое) значение F-статистики Фишера вычисляется по формуле:

.

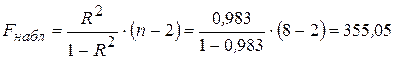
Табличное значение F-статистики при уровне значимости α = 0,01 и числе степеней свободы ν = n – 2 будет составлять 13,75 (F_кр = 13,75).

Так как F_набл > F_кр (355,05 > 13,75), то нулевая гипотеза Н₀ отклоняется и уравнение регрессионной модели признается статистически значимым и весьма надежным, поскольку наблюдаемое значение F-статистики превосходит табличное значение критерия более чем в 25 раз.

Дата добавления: 2016-06-02 ; просмотров: 2223 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ