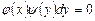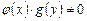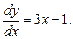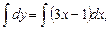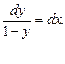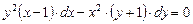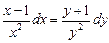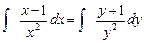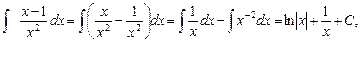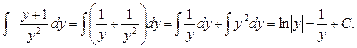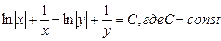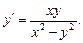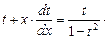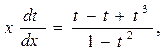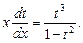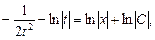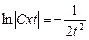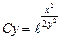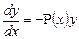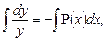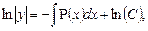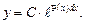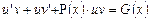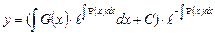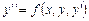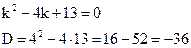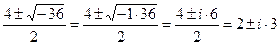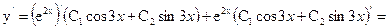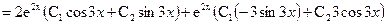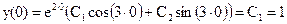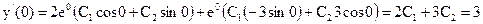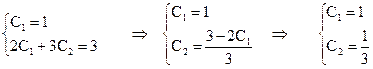Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Приложение №2
2. Валуце И. И., Дилигул Г. Д. Математика для техникумов. Учебное пособие.-М.: Наука. Гл. ред. физ.-мат. лит., 1999г.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов.- М.: Наука, 1970-2001, т. 1,2.
4. Кудрявцев В.А., Демидович Б.П. Краткий курс Высшей математики.- М.: Наука, 1989.
5. Данко П. Е., Попов А.Г., Кажевников Т.Я. Высшая математика в упражнениях и задачах. — М.:Наука,1999,ч.1,2
1.Основные понятия дифференциального уравнения.
Определение. Дифференциальное уравнения — это уравнение, связывающее функционально зависимые переменные и их производные.
Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком этого уравнения.
Если искомая функция зависит только от одного аргумента, то уравнение называется обыкновенным.
Мы будем решать только обыкновенные дифференциальные уравнения.
В общем случае обыкновенное дифференциальное уравнение n–го порядка может быть записано в виде F(x, y, y / ,y // . y ( n ) )=0 , где y(x)- неизвестная функция, F-некоторая функциональная зависимость между независимой переменнойx, функцией y и её производными.
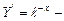

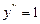
Определение: Функция, обращающая дифференциальное уравнение в тождество, называется решением этого уравнения.
2.Дифференциальные уравнения 1-го порядка с разделенными переменными.
В общем виде дифференциальное уравнение 1-го порядка можно записать как равенство F(x, y, y′) = 0
Дифференциальное уравнение вида f(x)dx = g(y)dy называют уравнением с разделёнными переменными.
Пример. Найти общее решение уравнения xdx+ydy=0
Разделим переменные, запишем уравнение в виде xdx = -ydy
Проинтегрируем обе части уравнения, получим
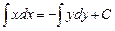
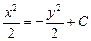
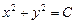
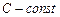
3.Дифференциальные уравнения 1-го порядка с разделяющими переменными.
Определение.Уравнением с разделяющимися переменными называется уравнение вида h(x)g(x) dx —
Чтобы привести это уравнение к уравнению с разделенными переменными достаточно разделить его на произведение
Пример.Найти общее решение уравнения y’ = 3x – 1
Представим производную у’ как 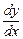
Чтобы разделить переменные, умножим обе части уравнения на dx. Полученное равенство проинтегрируем:
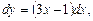
Ответ: 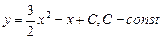
Пример.Найти решение уравнения y’+y-1=0.
Запишем уравнение в виде: y’ = 1 –y. Представим производную у’ как 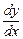
Уравнение примет вид 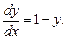
Найдём интегралы от обеих частей равенства:
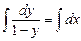
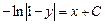
Ответ: 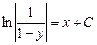
Пример.Найти общий интеграл (общее решение) уравнения
Вынесем за скобки общие множители:
Теперь разделим обе части уравнения на (y 2 ∙x 2 ) и сократим на x 2 и y 2 :
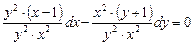
Проинтегрируем обе части отдельно:
Общий интеграл (решение) уравнения имеет вид:
Преобразуем по свойству логарифмов и получим:
Ответ: 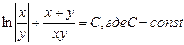
4.Однородные дифференциальные уравнения 1-го порядка
К уравнениям с разделяющимися переменными приводятся и так называемые однородные дифференциальные уравнения первого порядка.
Определение.Уравнение вида 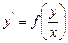
Такое уравнение подстановкой 

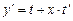
Пример.Найти общее решение дифференциального уравнения
Разделим правую часть уравнения (числитель и знаменатель) на x 2 . Получим уравнение 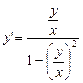
Выполним подстановки 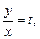
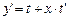
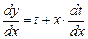
Перенесем t в правую часть и приведём дроби к общему знаменателю, то есть 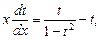
По основному свойству пропорции можно записать 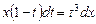
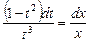
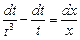
Проинтегрируем обе части равенства:
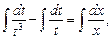
Выполним обратную подстановку 
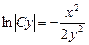
Выразим Cy, получим
Ответ:
6.Линейные дифференциальные уравнения 1-го порядка
Определение.Линейным дифференциальным уравнением 1-го порядка называется уравнение относительно неизвестной функции и её производной 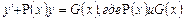
1)Если 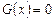
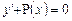
Это уравнение с разделяющимися переменными. Разделим переменные и выполним интегрирования отдельно каждой части уравнения:
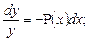
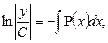
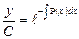
Если G(x)≠0, то уравнение 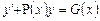
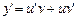
Сгруппируем слагаемые и получим уравнение 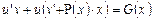
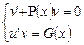
Теперь найдем v из первого уравнения системы (уравнение с разделяющимися переменными): 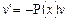
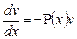
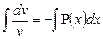
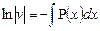
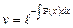
Подставим полученный результат во второе уравнение системы:
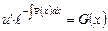
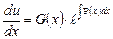

Теперь находим общее решение исходного уравнения, как произведение u на v:
7.Дифференциальные уравнения 2-го порядка
Дифференциальные уравнения 2-го порядка в общем виде можно записать как
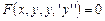
Линейным дифференциальным уравнением второго порядка называется уравнение вида 
Если 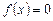
Пример. Найти общее и частное решения дифференциального уравнения
y» – 4y’ + 13y = 0, y(0) = 1, y ‘(0) = 3
Решение. Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Составим и решим характеристическое уравнение:
k1,2 =
Тогда общее решение уравнения: у = e 2 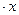
Для нахождения частного решения продифференцируем это выражение:
Из условий у(0) = 1, у'(0) = 3 находим
Поэтому частное решение данного дифференциального уравнения имеет вид:
Ответ:
Правила дифференцирования. Таблица производных и интегралов
| № | Функции | Производные |
| y = Cu | (Cu)’ = C(u)’ | |
| y = u ± v | (u ± v)’ = u’ ± v’ | |
| y = u ∙ v | (u ∙ v)’ = u’v + v’u | |
y = 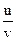 | 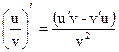 | |
| y = f(g(x)) | (f(g(x)))’ = 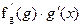 |
Производные элементарных функций
| (C)’ = 0 | 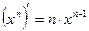 |
| (sin x) ‘ = cos x | (cos x) ‘ = — sin x |
(tg x) ‘ = 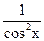 | (ctg x) ‘ = 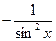 |
| (e x ) ‘ = e x | (a x )’ = a x ln(a) |
(lnx)’ = 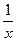 | 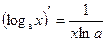 |
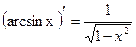 | 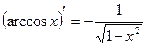 |
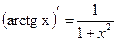 | 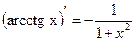 |
Неопределенные интегралы элементарных функций
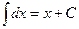 | 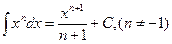 |
 | 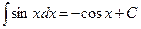 |
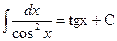 | 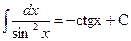 |
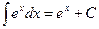 | 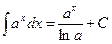 |
 | 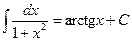 |
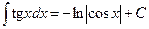 | 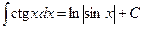 |
Решить дифференциальные уравнения и выбрать правильный ответ:
1.
a) 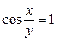

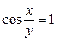
2.
a) 
3.
a) 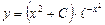
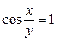
Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»
Разделы: Математика
I. Обыкновенные дифференциальные уравнения
1.1. Основные понятия и определения
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Решением дифференциального уравнения называется такая функция 
Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение
1. Рассмотрим дифференциальное уравнение первого порядка
Решением этого уравнения является функция y = 5 ln x. Действительно, 

А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.
2. Рассмотрим дифференциальное уравнение второго порядка y» — 5y’ +6y = 0. Функция 
Действительно, 
Подставляя эти выражения в уравнение, получим: 

А это и значит, что функция 
Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.
Общим решением дифференциального уравнения называется функция вида 
Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.
График частного решения дифференциального уравнения называется интегральной кривой.
1.Найти частное решение дифференциального уравнения первого порядка
xdx + ydy = 0, если y = 4 при x = 3.
Решение. Интегрируя обе части уравнения, получим
Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде 

Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 3 2 + 4 2 = C 2 ; C=5.
Подставляя С=5 в общее решение, получим x 2 +y 2 = 5 2 .
Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.
2. Найти общее решение дифференциального уравнения
Решением этого уравнения является всякая функция вида 



Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство 

Например, непосредственной подстановкой можно убедиться, что функции 

Задача, в которой требуется найти частное решение уравнения y’ = f(x,y) удовлетворяющее начальному условию y(x0) = y0, называется задачей Коши.
Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x0) = y0, называется решением задачи Коши.
Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y’ = f(x,y) при условии y(x0) = y0,, означает найти интегральную кривую уравнения y’ = f(x,y) которая проходит через заданную точку M0(x0,y0).
II. Дифференциальные уравнения первого порядка
2.1. Основные понятия
Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.
В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.
Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.
Общим решением дифференциального уравнения первого порядка называется функция вида 
Пример. Рассмотрим дифференциальное уравнение первого порядка 
Решением этого уравнения является функция 
Действительно, заменив в данном уравнении, 


Следовательно, функция 

Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1 в общее решение уравнения 

Таким образом, частное решение получим из общего 


2.2. Дифференциальные уравнения с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы 
Для тех y, для которых 

Уравнение вида 
Проинтегрировав обе части уравнения 

Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными
- Производную функции переписать через её дифференциалы
- Разделить переменные.
- Проинтегрировать обе части равенства, найти общее решение.
- Если заданы начальные условия, найти частное решение.
Решить уравнение y’ = xy
Решение. Производную функции y’ заменим на
разделим переменные
проинтегрируем обе части равенства:
Ответ:
Найти частное решение уравнения
Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде 
Интегрируя обе части последнего равенства, найдем
Подставив начальные значения x0 = 1, y0 = 3 найдем С 9=1-1+C, т.е. С = 9.
Следовательно, искомый частный интеграл будет 
Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом
Решение. Согласно условию
Это уравнение с разделяющимися переменными. Разделив переменные, получим:
Проинтегрировав обе части уравнения, получим:
Используя начальные условия, x = 2 и y = — 3 найдем C:
Следовательно, искомое уравнение имеет вид
2.3. Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)
где f(x) и g(x) — некоторые заданные функции.
Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид: y’ = f(x)y
Если 
Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: 
В частности, если С =0, то решением является y = 0 Если линейное однородное уравнение имеет вид y’ = ky где k — некоторая постоянная, то его общее решение имеет вид: 
Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой 
т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения 
Для линейного неоднородного уравнения вида 
где k и b— некоторые числа и 


Пример. Решить уравнение y’ + 2y +3 = 0
Решение. Представим уравнение в виде y’ = -2y — 3 где k = -2, b= -3 Общее решение задается формулой 
Следовательно, 
Ответ:
2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли
Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v — неизвестные функции от x. Этот метод решения называется методом Бернулли.
Алгоритм решения линейного дифференциального уравнения первого порядка
1. Ввести подстановку y=uv.
2. Продифференцировать это равенство y’ = u’v + uv’
3. Подставить y и y’ в данное уравнение: u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).
4. Сгруппировать члены уравнения так, чтобы u вынести за скобки:
5. Из скобки, приравняв ее к нулю, найти функцию
Это уравнение с разделяющимися переменными:
Разделим переменные и получим:
Откуда 

6. Подставить полученное значение v в уравнение 
и найти функцию 
7. Записать общее решение в виде: 

Найти частное решение уравнения y’ = -2y +3 = 0 если y =1 при x = 0
Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’
Подставляя y и y’ в данное уравнение, получим
Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки
Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)
Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: 
Подставим полученное значение v в уравнение 
Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: 


Ответ:
III. Дифференциальные уравнения высших порядков
3.1. Основные понятия и определения
Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y») = 0
Общим решением дифференциального уравнения второго порядка называется функция вида 
Частным решением дифференциального уравнения второго порядка называется решение, полученное из общего 
3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y» + py’ +qy = 0, где pи q— постоянные величины.
Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
1. Записать дифференциальное уравнение в виде: y» + py’ +qy = 0.
2. Составить его характеристическое уравнение, обозначив y» через r 2 , y’ через r, yчерез 1: 
3.Вычислить дискриминант D = p 2 -4q и найти корни характеристического уравнения; при этом если:
а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня 

б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни 
Общее решение
Дифференцируя общее решение, получим
Составим систему из двух уравнений
Подставим вместо 




Таким образом, искомым частным решением является функция

2. Найти частное решение уравнения