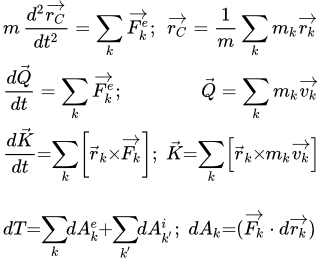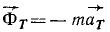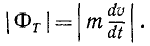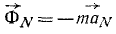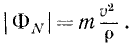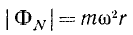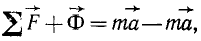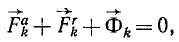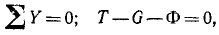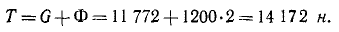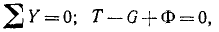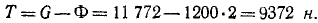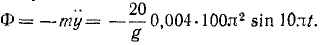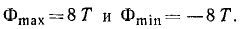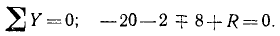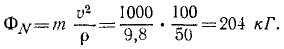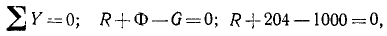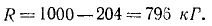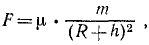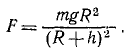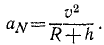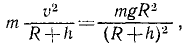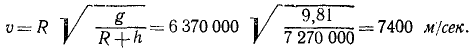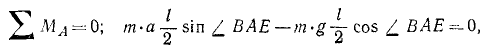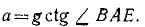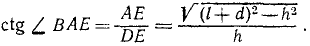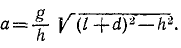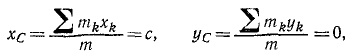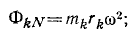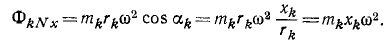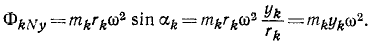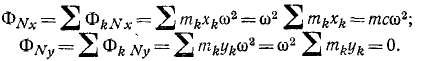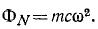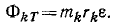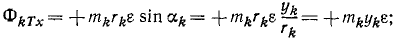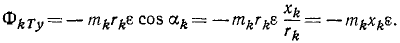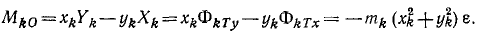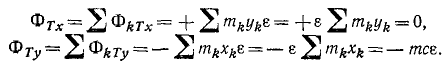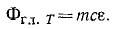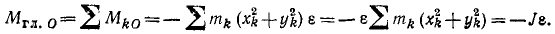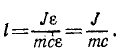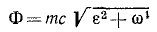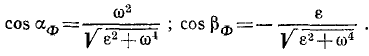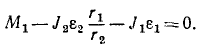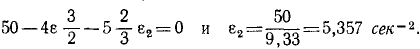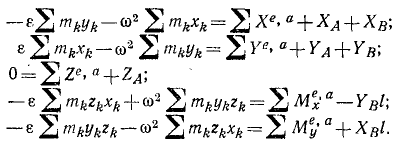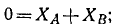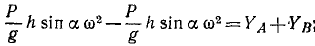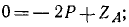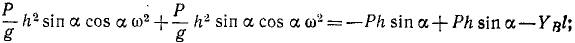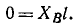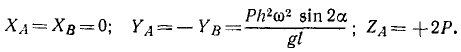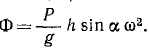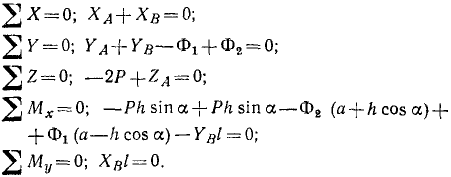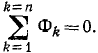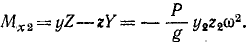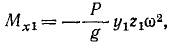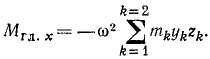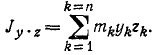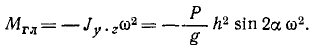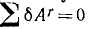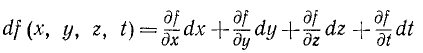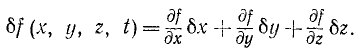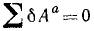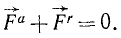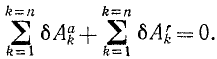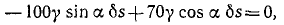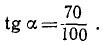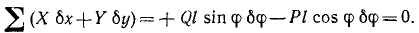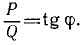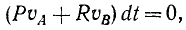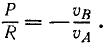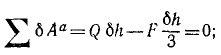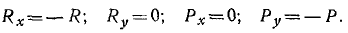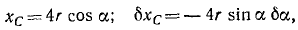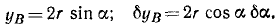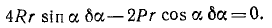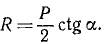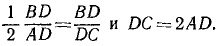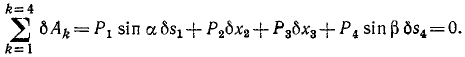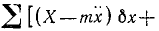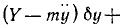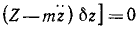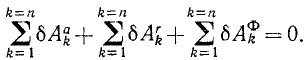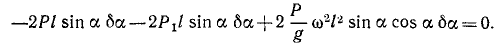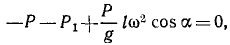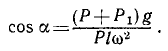iSopromat.ru
Рассмотрим общее уравнение динамики механической системы, которое также называется принципом Даламбера-Лагранжа:
Объединяя этот принцип с принципом возможных перемещений для систем с идеальными связями получаем уравнение:
которое называют общим уравнением динамики (или принципом Даламбера-Лагранжа).
При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и сил инерции на любом возможном перемещении системы будет равна нолю.
Поскольку в уравнении присутствуют силы инерции, а следовательно и ускорения, то эти уравнения представляют собой дифференциальные уравнения движения механической системы с идеальными связями.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Динамика твердого тела и системы. Все определения, законы и теоремы
Механическая система. Основные понятия
Свойства внутренних сил
Приводимые ниже свойства внутренних сил являются третьим законом Ньютона для системы материальных точек.
Свойство 1
Векторная сумма (главный вектор) всех внутренних сил системы равна нулю:
.
Свойство 2
Векторная сумма моментов всех внутренних сил системы, относительно произвольной точки O равена нулю:
.
Дифференциальные уравнения движения точек системы
Согласно второму закону Ньютона, дифференциальное уравнение движения материальной точки k массой mk , входящей в систему, имеет вид:
.
Спроектировав это уравнение на оси декартовой системы координат Oxyz , получим для каждой точки три уравнения:
.
Общие теоремы динамики механической системы
Общие теоремы динамики – это теорема о движении центра масс механической системы, теорема об изменении количества движения, теорема об изменении главного момента количества движения (кинетического момента) и теорема об изменении кинетической энергии механической системы.
Теорема о движении центра масс механической системы
Теорема о движении центра масс механической системы
Произведение массы системы на ускорение ее центра масс равно векторной сумме всех действующих на систему внешних сил:
.
Здесь – масса системы; – ускорение центра масс системы: ;
– скорость центра масс системы: ;
– радиус вектор (координаты) центра масс системы: ;
– координаты и массы точек, из которых состоит система.
Теорема об изменении количества движения (импульса)
Теорема об изменении количества движения в дифференциальной форме
Производная по времени от количества движения (импульса) системы равна векторной сумме всех действующих на систему внешних сил:
.
Теорема об изменении количества движения в интегральной форме
Изменение количества движения (импульса) системы за некоторый промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени:
.
Закон сохранения количества движения (импульса)
Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения.
Если сумма проекций внешних сил на какую-либо ось равна нулю, то проекция количества движения системы на эту ось будет постоянной.
Тело переменной массы. Движение ракеты
Уравнение Мещерского
Дифференциальное уравнение движения точки переменной массы называется уравнением Мещерского:
.
Здесь – масса тела, которая является функцией от времени t ; – векторная сумма приложенных к телу внешних сил; – скорость отделяющихся частиц относительно тела.
Реактивная сила направлена в сторону, противоположную истечению отделяющихся частиц (топлива), и определяется по формуле:
,
где – расход топлива (кг/с).
Формула Циолковского
Скорость v движения ракеты под действием одной только реактивной силы определяется по формуле Циолковского:
.
Здесь – начальная скорость ракеты; u – скорость истечения реактивных газов относительно ракеты; – масса сгоревшего топлива; – масса корпуса ракеты с остатками топлива. Когда топливо выгорает полностью, то – это масса корпуса ракеты с полезной нагрузкой.
Отношение первоначальной массы ракеты (с полным запасом топлива) к массе корпуса ракеты называется числом Циолковского:
.
Для достижения первой космической скорости км/с , при , требуется, чтобы скорость истечения реактивных газов была не менее км/с . В современных жидкостных двигателях удается получить скорость истечения км/с . Поэтому, для достижения космических скоростей, ракеты должны быть многоступенчатыми.
Теорема об изменении главного момента количества движения (теорема моментов)
Теорема моментов в инерциальной системе координат
Главный момент количества движения (или кинетический момент) системы является характеристикой вращательного движения. Возьмем систему координат Oxyz с началом в точке O . Тогда , проекции кинетического момента системы на оси координат являются моментами количества движения системы относительно этих осей:
;
;
.
Если система состоит из нескольких частей, то главный момент количества движения системы равен сумме моментов количеств движения отдельных ее частей.
Теорема об изменении главного момента количества движения (теорема моментов)
Производная по времени от главного момента количества движения системы относительно некоторого неподвижного центра O равна сумме моментов всех внешних сил системы относительно того же центра:
(М2) .
Выпишем компоненты уравнения (М2) в неподвижной системе координат Oxyz :
;
;
.
Закон сохранения главного момента количества движения (момента импульса)
Если сумма моментов всех приложенных к системе внешних сил относительно данного неподвижного центра O равна нулю, то главный момент количества движения системы относительно этого центра будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения:
.
Часто встречаются случаи, когда система вращается вокруг неподвижной оси. Тогда нужно спроектировать векторное уравнение (М2) на направление этой оси. В результате получим теорему моментов, применительно к вращению относительно оси.
Производная по времени от кинетического момента системы относительно некоторой неподвижной оси равна сумме моментов всех внешних сил системы относительно этой оси. Если сумма моментов всех приложенных к системе внешних сил относительно некоторой неподвижной оси равна нулю, то кинетический момент системы относительно этой оси будет постоянным.
Теорема моментов в системе координат, связанной с центром масс
Кинетический момент системы относительно неподвижного центра удобно использовать в тех задачах, в которых система имеет одну или несколько закрепленных точек. Например при вращении тела или системы тел вокруг точки или оси. Когда таких точек нет, то наиболее удобным в использовании является кинетический момент относительно центра масс в системе координат, в которой центр масс покоится, а оси остаются параллельными осям инерциальной системы отсчета. В общем случае, система отсчета, связанная с центром масс, не является инерциальной, но она не вращается относительно инерциальной системы отсчета.
Главным моментом количества движения системы относительно ее центра масс C называется величина , равная векторной сумме моментов количеств движения всех точек системы относительно центра масс в системе отсчета, в которой центр масс покоится, а оси системы координат параллельны осям инерциальной системы координат:
(М3) .
Здесь – скорости точек системы и скорость ее центра масс в инерциальной системе отсчета. Тогда – скорость точки массой в системе отсчета, связанной с центром масс.
Связь кинетических моментов в различных системах отсчета
Кинетический момент системы относительно неподвижной точки O равен сумме кинетического момента центра масс C , если в нем сосредоточить всю массу системы, и кинетического момента системы относительно центра масс :
(М4) .
То есть можно сказать, что вращение системы вокруг неподвижной точки O складывается из вращения центра масс C вокруг точки O , и вращения элементов системы вокруг центра масс C .
В (М2) ⇑ мы использовали кинетический момент системы, вычисляемый относительно произвольной неподвижной точки в инерциальной системе отсчета. Уравнения для кинетического момента имеют тот же вид, если в качестве полюса взять центр масс C системы.
Теорема моментов относительно центра масс системы
Производная по времени от главного момента количества движения системы относительно ее центра масс C , равна сумме моментов всех внешних сил системы относительно того же центра:
(М5) .
В (М5) мы используем неинерциальную систему координат, начало которой, в течении всего движения системы, находится в центре масс, а оси параллельны осям инерциальной системы координат. Естественно, что если мы выберем инерциальную систему координат, начало которой в данный момент времени совпадает с центром масс, то теорема моментов не изменит своего вида (М5). То есть центр масс обладает такой особенностью, что теорема моментов относительно него имеет одну и ту же форму, как в инерциальной системе отсчета, так и в неинерциальной системе, начало которой на всем протяжении движения совпадает с центром масс, а оси параллельны осям инерциальной системы отсчета. Такая особенность возникает только для центра масс системы. Для других точек, уравнение моментов в неинерциальной системе отсчета не имеет вида (М5).
Кинетический момент твердого тела
Пусть твердое тело вращается с угловой скоростью ω вокруг неподвижной оси Oz . Тогда его кинетический момент относительно этой оси равен произведению момента инерции относительно этой оси на угловую скорость вращения:
.
Если на твердое тело действуют внешние силы, то применяя теорему моментов, находим:
.
Если момент сил относительно оси Oz равен нулю: , то угловая скорость постоянна: .
В произвольном случае, кинетический момент выражается через компоненты угловой скорости и тензора инерции. Пусть, в данный момент времени, скорость точки O тела равна нулю: . То есть точка O является мгновенным центром вращения тела. Тогда компоненты кинетического момента тела относительно точки O определяется по формуле:
.
Здесь – компоненты тензора инерции тела ⇑ относительно точки O . Они связаны с моментами инерции формулами ⇑. Также подразумевается, что индексы p, q принимают значения x, y, z :
.
Здесь мы выбрали в качестве полюса неподвижную (в рассматриваемый момент времени) точку. Если, в качестве полюса выбрать центр масс тела, то компоненты момента импульса определяются по аналогичной формуле:
.
Для других точек, момент импульса выражается через угловую скорость более сложным образом.
В большинстве случаев, наиболее удобным полюсом оказывается центр масс C тела. Тогда, для компонент кинетического момента относительно произвольного центра O , имеем:
.
Здесь – радиус-вектор, проведенный из точки O в точку центра масс C ; m – масса тела; – скорость центра масс; – компоненты тензора инерции относительно точки C . Как видно, первое слагаемое является кинетическим моментом материальной точки, находящейся в центре масс тела и движущейся со скоростью центра масс. Второе слагаемое является вкладом вращения тела относительно его центра масс. То есть, как было указано выше ⇑, кинетический момент твердого тела относительно произвольной неподвижной точки O равен сумме кинетического момента поступательного движения центра масс относительно точки O и кинетического момента вращательного движения тела относительно его центра масс.
Теорема об изменении кинетической энергии
Кинетической энергия системы
Если система состоит из нескольких тел, то кинетическая энергия системы равна сумме кинетических энергий тел, составляющих систему.
Теорема Кенига
Кинетическая энергия системы равна сумме кинетической энергии центра масс C системы, масса m которого равна массе всей системы: , и кинетической энергии этой системы в ее движении относительно центра масс:
.
Здесь – скорость движения центра масс.
Если тело массы m совершает поступательное движение со скоростью , то скорости всех его точек равны . Кинетическая энергия поступательного движения:
(К1) .
Если тело вращается с угловой скоростью ω вокруг неподвижной оси Oz , то кинетическая энергия вращательного движения определяется по формуле:
(К2) ,
где – момент инерции тела относительно оси вращения.
В произвольном случае, кинетическая энергия равна сумме кинетической энергии поступательного движения центра масс и энергии вращательного движения относительно центра масс:
(К3) .
Здесь ω – абсолютное значение угловой скорости вращения тела; CL – ось, проведенная через центр масс, параллельно направлению вектора угловой скорости; – момент инерции относительно оси CL . Направление оси вращения может меняться со временем. Указанная формула дает мгновенное значение кинетической энергии.
Формула (К3) удобна, если тело вращается вокруг неподвижной оси. Если же вектор угловой скорости может менять направление относительно тела, то нам пришлось бы вычислять момент инерции относительно каждого положения оси вращения. В этом случае удобно выразить кинетическую энергию вращения через компоненты тензора инерции относительно центра масс тела:
(К4) .
Работа сил и мощность
Все сказанное в отношении работы и потенциальной энергии в разделе «Динамика материальной точки», имеет место и для динамики системы тел.
См. Работа силы. Мощность Силовые поля и потенциальная энергия
Единственное отличие заключается в том, что там силы приложены только к одной исследуемой точке. Для системы, внешние силы могут быть приложены к разным точкам, составляющих систему. При этом одна сила приложена только к одной точке, но этих сил может быть много. Точку, к которой приложена сила называют точкой приложения силы.
При рассмотрении твердых тел, мы можем упростить реальную систему сил, воспользовавшись результатами статики. Для этого нужно преобразовать сложную систему реальных сил на эквивалентную ей, более простую, систему. Так например, систему сил тяжести, действующих на каждую точку тела, можно заменить одной равнодействующей силой, приложенной к центру масс тела. Тогда все вычисления можно выполнять только для одной силы с точкой приложения в центре масс тела.
Работа при перемещении точки
Элементарная работа , которую совершает сила , при элементарном перемещении ее точки приложения, равна скалярному произведению векторов силы и перемещения:
;
.
То есть она равна произведению модуля вектора силы , перемещения и косинусу угла между ними. Это, в свою очередь, равно произведению касательной компоненты силы к траектории движения, и модуля элементарного перемещения . Здесь – скорость точки приложения силы; – промежуток времени, в течении которого происходит перемещение.
Мощность равна скалярному произведению векторов силы и скорости:
.
Работа , которую совершает сила , при перемещении точки ее приложения из точки в точку , равна сумме (интегралу) элементарных работ:
.
Работа при движении тела
Если тело движется поступательно, то скорости и перемещения всех его точек равны. В этом случае, работа и мощность вычисляются также как и при перемещении точки. Этот случай рассмотрен выше.
Для тела, вращающегося вокруг неподвижной оси Oz , элементарная работа равна произведению момента силы относительно этой оси на элементарный угол поворота dφ :
.
Здесь – мгновенное значение угловой скорости вращения; dt – время, в течении которого происходит поворот на угол dφ .
Мощность равна произведению момента силы на угловую скорость:
.
Для тела, вращающегося вокруг неподвижной точки O , элементарная работа равна скалярному произведению вектора момента силы относительно этой точки на вектор элементарного угла поворота :
.
Вектор элементарного поворота направлен вдоль вектора мгновенной угловой скорости : .
Мощность равна скалярному произведению векторов момента силы и угловой скорости:
.
При произвольном движении твердого тела, мы, произвольным образом, выбираем точку O , связанную с телом, которую называем полюсом. Тогда элементарная работа равна работе, которую совершает сила при перемещении полюса , и работе момента силы относительно полюса при элементарном повороте тела:
.
Заметим, что элементарный угол поворота и угловая скорость вращения не зависят от выбора полюса.
Мощность:
.
Теорема об изменении кинетической энергии системы
Теорема об изменении кинетической энергии системы в дифференциальной форме.
Дифференциал (приращение) кинетической энергии системы при некотором ее перемещении равно сумме дифференциалов работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.
Теорема об изменении кинетической энергии системы в интегральной форме.
Изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.
Неизменяемая система – это механическая система, в которой расстояние между любыми двумя взаимодействующими точками остается постоянным во все время движения.
Идеальные связи – это связи, для которых сумма элементарных работ их реакций на любом возможном перемещении системы равна нулю.
Для систем с идеальными связями и неизменяемых систем, сумма работ внутренних сил равна нулю: . Для таких систем, изменение кинетической энергии системы равно сумме работ всех внешних сил, приложенных к системе:
.
Коэффициент полезного действия
В машинах и механизмах, совершающих некоторую полезную работу, силы можно разделить на следующие виды.
Движущие силы – это силы, совершающие положительную работу Aзатр .
Силы полезного сопротивления – это силы, совершающие отрицательную работу – Aпол. сопр , но выполняют полезное действие.
Силы вредного сопротивления – это силы, совершающие отрицательную работу – Aвр. сопр , и не выполняющие полезных действий.
Попеременные силы – это силы, совершающие то положительную, то отрицательную работу, но за достаточно большой промежуток времени, их сумма работ равна нулю. Механический коэффициент полезного действия машины – это величина, равная отношению работы полезных сил сопротивления (полезной работы) к работе движущих сил (затраченной на приведение машины в движение):
.
Пусть Nмаш – полезная мощность машины; Nдв – мощность двигателя. Тогда
.
Закон сохранения полной механической энергии
Если система движется под действием потенциальных сил, то сумма кинетической T и потенциальной Π энергий сохраняет постоянное значение:
.
Механическая энергия – это сумма кинетической и потенциальной энергии.
Уменьшение механической энергии, как правило, связано с ее превращением в тепловую, электрическую, электромагнитную энергию, энергию звука и электромагнитных колебаний (свет, электромагнитные волны). Увеличение механической энергии связано с обратными процессами превращения различных видов энергии в механическую.
Геометрия масс
Моменты и тензор инерции твердого тела
В этом разделе мы рассматриваем величины, характеризующие распределение массы системы в пространстве.
Сложившаяся система обозначений
Тензор инерции твердого тела
Для вычисления момента импульса и кинетической энергии твердого тела, нам нужно знать всего несколько характеристик тела, величины которых зависят от распределения масс точек, составляющих тело. Эти величины составляют компоненты, так называемого, тензора инерции , который определяется относительно некоторого, предварительно выбранного, центра O , и вычисляется по формуле:
(И1) .
Здесь – координаты точки массы в декартовой системе координат, с началом в выбранном центре O ; при p = q , при p ≠ q . Индексы координат нумеруют цифрами, придерживаясь следующих обозначений:
.
Тензор инерции имеет следующие шесть компонент:
;
;
.
Если в качестве полюса O выбрать центр масс C тела, то компоненты момента импульса и кинетическая энергия тела T вычисляются по относительно простым формулам:
.
Здесь – скорость центра масс тела, – компоненты угловой скорости.
Моменты инерции твердого тела
Пользоваться тензором инерции (И1) ⇑ удобно, поскольку, при решении задач, мы сразу можем применить результаты теории тензорного исчисления. Однако сложилось так, что вместо тензора инерции вводят его отдельные компоненты, придав им специфические названия и обозначения.
Осевые моменты инерции:
;
Центробежные моменты инерции:
.
Все это может привести к путанице. Поэтому компоненты тензора инерции мы будем обозначать буквой I . А сложившиеся названия и обозначения его отдельных компонент – буквой J .
Определения моментов инерции
Свойства моментов инерции
Сумма осевых моментов инерции
Знаки моментов инерции
Осевые моменты инерции не могут быть отрицательными:
.
Центробежные моменты инерции могут быть положительными, отрицательными, или равными нулю.
Симметричность моментов инерции
Центробежные моменты инерции симметричны относительно своих индексов:
.
Все моменты инерции имеют размерность [кг·м 2 ].
Для вычисления моментов инерции сплошных тел, мы от суммирования переходим к интегрированию. При этом массу точки mk мы заменяем на дифференциал: . Дифференциал массы dm выражаем через плотность μ и элемент объема : . Далее интегрируем по объему тела V :
.
Моменты инерции в разных системах координат
Если мы от начальной системы координат Oxyz перейдем к другой системе O′x′y′z′ , то величины моментов инерции в новой системе будут отличаться от моментов в старой системе координат. Такие переходы называются преобразованиями системы координат.
Повороты системы координат
Сначала рассмотрим случай, когда две декартовы системы координат Oxyz и Ox′y′z′ имеют общее начало O . То есть вторая система получена из первой поворотом вокруг общего центра O . Согласно тензорной алгебре, любой симметричный тензор, поворотом системы координат можно привести к диагональному виду. То есть можно найти такую декартову систему координат, относительно которой все центробежные моменты равны нулю. Оси такой системы координат называются главными осями инерции тела.
Главная ось инерции тела , относительно некоторой точки O – это ось, для которой оба центробежных момента инерции, содержащие индекс этой оси, равны нулю. Например, если ось z – главная ось инерции, то .
Главный момент инерции тела , относительно некоторой точки O – это момент инерции относительно главной оси инерции.
Главная центральная ось инерции тела – это главная ось, проходящая через центр масс тела.
Главный центральный момент инерции тела – это момент инерции относительно главной центральной оси инерции.
Любое тело в пространстве имеет три главные оси инерции и три значения главных моментов инерции (относительно предварительно выбранной точки O ). При этом главные моменты инерции могут иметь равные значения.
Стоит подчеркнуть, что главные оси определяются относительно определенной точки тела. При выборе другой точки, главные оси могут иметь другие направления.
Тело с плоскостью симметрии
Если распределение массы тела в пространстве имеет плоскость симметрии, то любая ось, перпендикулярная к этой плоскости, будет главной осью инерции тела, а две другие главные оси лежат в плоскости симметрии.
Тело с осью симметрии
Если распределение массы тела в пространстве имеет ось симметрии, то эта ось является главной центральной осью инерции.
Параллельность главных осей
Если точка O расположена на главной центральной оси тела, то главные оси, проходящие через эту точку, параллельны главным центральным осям.
Главная ось, не проходящая через центр масс
Главная ось инерции, не проходящая через центр масс тела, является главной осью инерции только в одной точке.
Инвариантность суммы осевых моментов инерции
Если от одной системы координат Oxyz , мы перейдем к другой Ox′y′z′ с тем же началом, то сумма осевых моментов инерции не изменится при переходе от одной системы к другой:
.
По этой причине, величина полярного момента инерции не зависит от поворотов системы координат. То есть является инвариантом относительно поворотов системы координат. Она зависит от выбранного центра, относительно которого определяются моменты инерции.
Момент инерции относительно произвольной оси
Пусть нам известны моменты инерции тела относительно осей Oxyz . И пусть OL – произвольная ось, проходящая через начало O , составляющая углы с осями Ox, Oy, Oz . Тогда момент инерции тела относительно оси OL определяется по формуле:
.
Если оси x,y,z являются главными осями, то
.
Перенос системы координат. Теорема Гюйгенса-Штейнера
Отсюда следует, что осевой момент инерции будет иметь наименьшее значение относительно той оси, которая проходит через центр масс тела.
Моменты инерции некоторых тел
Однородный стержень
Рассмотрим тонкий однородный стержень длины l и массы m . Выберем начало координат O на одном из его концов. Направим ось Ox вдоль стержня; оси Oy и Oz – перпендикулярно. Эти оси будут главными осями инерции стержня относительно центра O . Осевые моменты инерции имеют следующие значения:
.
Центр масс стержня находится по его середине, в точке C ; . Проведем через нее оси координат Cxy′z′ , параллельные предыдущим. Эти оси являются главными центральными осями инерции со следующими значениями осевых моментов:
.
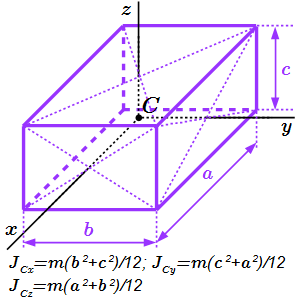
Прямоугольный параллелепипед
Рассмотрим прямоугольный параллелепипед с длинами ребер a, b, c (см. рисунок). Его центр масс C находится в центре параллелепипеда. Оси, проведенные через центр масс параллельно сторонам, будут главными центральными осями инерции. Моменты инерции прямоугольного параллелепипеда:
.
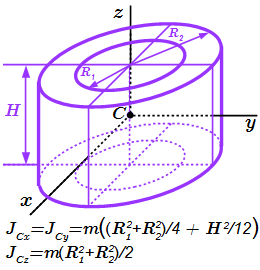
Полый цилиндр
Рассмотрим полый цилиндр высоты H и радиусами . Его центр масс находится на оси цилиндра, на расстоянии от основания. Через точку C проводим главные центральные оси инерции: ось Cz – вдоль оси цилиндра; оси Cx, Cy – перпендикулярно. Моменты инерции полого цилиндра:
.
Однородный сплошной диск
Тонкий обруч
Динамика твердого тела
Свободное движение твердого тела
Рассмотрим твердое тело массы m , перемещение которого не ограничено в пространстве. Пусть на тело действуют внешние силы , приложенных в точках . Для определения уравнений движения, мы воспользуемся теоремой о движении центра масс ⇑, теоремой моментов относительно центра масс системы ⇑, и выражением кинетического момента тела через компоненты угловой скорости ωq и тензора инерции Ipq тела (в системе координат с началом в центре масс, оси которой параллельны осям неподвижной системы):
(Т1) ;
(Т2) ;
(Т3) .
Здесь – радиус-вектор, проведенный в центр масс тела.
При известных внешних силах , из уравнения (Т1) можно определить закон движения центра масс тела.
Уравнения (Т2)–(Т3) определяют закон движения тела при его вращении. Они записаны в системе отсчета, начало которой находится в центре масс C , а оси параллельны осям инерциальной системы отсчета. Чтобы ими воспользоваться, мы должны найти способ, с помощью которого можно задать положение тела при его вращении. Это можно сделать с помощью углов Эйлера. Тогда оси вращающейся системы координат, связанной с телом, удобно направить вдоль главных центральных осей инерции тела ⇑. Тогда правые части уравнений (Т3) будут выражаться через главные центральные моменты инерций тела ⇑, три угла Эйлера и их производные по времени. Дифференцируя (Т3) и подставляя в (Т2), получим систему дифференциальных уравнений второго порядка для трех углов Эйлера.
Поступательное движение твердого тела
Рассмотрим поступательное движение твердого тела. Для него угловая скорость и угловое ускорение равны нулю: . Тогда момент количества движения постоянен и равен нулю: . Из (Т2) следует, что и главный момент всех внешних сил относительно центра масс должен равняться нулю: .
Дифференциальные уравнения поступательного движения определяются по формулам (Т1) ⇑:
.
Здесь – проекции внешней силы на оси координат. При поступательном движении, все точки тела имеют равные скорости и равные ускорения. Потому определив закон движения одной точки – центра масс , мы получаем закон движения произвольной точки A :
.
Плоское движение твердого тела
Рассмотрим плоское движение твердого тела. Выберем инерциальную систему координат Oxyz . Оси Ox и Oy направим в плоскости движения. Тогда положение тела полностью определяется тремя величинами – двумя компонентами радиус-вектора центра масс C : ; и углом поворота φ . Внешние силы также лежат в рассматриваемой плоскости. Кинетический момент направлен вдоль оси z и выражается через угловую скорость и момент инерции относительно оси, проходящей через центр масс C , перпендикулярно плоскости движения: .
Уравнения (Т1)-(Т3) ⇑ принимают вид:
(Т4) ;
(Т5) .
Здесь – проекции внешней силы на оси координат; – это алгебраический момент силы относительно центра C – то есть проекция момента силы на ось Oz .
Вращение твердого тела вокруг неподвижной оси
Рассмотрим вращение твердого тела вокруг неподвижной оси Oz . Выберем декартову систему координат. Ось Oz направим вдоль оси вращения; оси Ox и Oy – перпендикулярно. Считаем, что перемещение параллельно оси вращения отсутствует. Тогда это плоское движение. Оно происходит в плоскости Oxy . Положение тела определяется только углом поворота φ вокруг оси вращения.
Применяя теорему моментов ⇑ и связь момента с угловой скоростью ⇑, получим дифференциальное уравнение вращения твердого тела вокруг неподвижной оси:
(Т6) .
Здесь – момент инерции тела относительно оси вращения; – вращающий момент – то есть сумма моментов всех внешних сил относительно оси вращения.
Вводя угловое ускорение , дифференциальное уравнение вращения примет вид:
.
Оно аналогично уравнению прямолинейного движения под действием силы Fx :
.
Если вращающий момент является постоянной величиной: , то уравнение (Т6) имеет решение:
.
Здесь – угол поворота и угловая скорость вращения в начальный момент времени ; – угловое ускорение, постоянная величина.
Физический и математический маятники
Далее мы будем приводить данные только для плоского движения маятника. То есть мы считаем, что маятник совершает колебания вокруг неподвижной оси.
Уравнение вращательного движения физического маятника имеет вид:
.
Здесь ось вращения проходит через точку O ; φ – угол поворота между осью маятника и вертикальной прямой; JO – момент инерции маятника относительно оси вращения; P =mg – сила тяжести, действующая на маятник массы m ; a – расстояние от оси вращения O до центра масс C маятника; g – ускорение свободного падения. Введем обозначение: . Тогда
.
Рассмотрим малые колебания . При этом . И мы получаем уравнение гармонических колебаний:
.
Общее решение этого уравнения имеет вид:
.
Здесь – постоянные, которые определяются из начальных условий.
Во многих случаях удобно выразить общее решение уравнения малых колебаний через амплитуду α и начальную фазу колебаний β :
.
Величина k называется угловой частотой колебаний. Период колебаний: . Для малых колебаний, период не зависит от амплитуды. Этот результат является приближенным. При увеличении амплитуды такая зависимость появляется.
Математический маятник – это материальная точка, подвешенная на нерастяжимой невесомой нити, и совершающая колебания под действием силы тяжести. 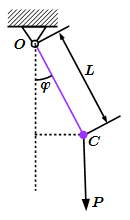
Математический маятник является частным случаем физического маятника. Пусть L – длина нити математического маятника. Его центр масс C находится в материальной точке: L = |OC| . Момент инерции: . Выразив силу тяжести P через массу m и ускорение свободного падения g , получим угловую частоту колебаний:
.
Теперь вернемся к физическому маятнику. Если положить , то частота физического маятника будет совпадать с частотой математического маятника длины L :
.
Приведенная длина физического маятника – это длина математического маятника, частота колебаний которого совпадает с частотой колебаний рассматриваемого физического маятника.
Центром качаний физического маятника называется точка K на оси физического маятника, находящаяся на расстоянии его приведенной длины от точки подвеса.
Свойство взаимности
Если физический маятник подвесить за центр качаний K , то его частота колебаний не изменится, а прежняя точка подвеса O станет центром качаний нового маятника.
Положение центра качания
Центр качаний всегда расположен ниже центра масс:
.
Принцип Даламбера
Суть принципа Даламбера состоит в том, чтобы задачи динамики свести к задачам статики. Для этого предполагают (или это заранее известно), что тела системы имеют определенные (угловые) ускорения. Далее вводят силы инерции и (или) моменты сил инерции, которые равны по величине и обратные по направлению силам и моментам сил, которые по законам механики создавали бы заданные ускорения или угловые ускорения
Принцип Даламбера
Если в любой момент времени к каждой точке системы приложить силы инерции и реально действующие силы, то полученная система сил будет находиться в равновесии, и к ней можно применять уравнения статики.
Рассмотрим пример. Путь тело массы m совершает поступательное движение и на него действуют внешние силы . Далее мы предполагаем, что эти силы создают ускорение центра масс системы . По теореме о движении центра масс, центр масс тела имел бы такое же ускорение, если бы на тело действовала сила . Далее мы вводим силу инерции:
.
После этого задача динамики:
.
Превращается в задачу статики:
;
.
Для вращательного движения поступают аналогичным образом. Пусть тело вращается вокруг оси z и на него действуют внешние моменты сил . Мы предполагаем, что эти моменты создают угловое ускорение εz . Далее мы вводим момент сил инерции M И = – Jz εz . После этого задача динамики:
.
Превращается в задачу статики:
;
.
Принцип возможных перемещений
Принцип возможных перемещений применяется для решений задач статики. В некоторых задачах, он дает более короткое решение, чем составление уравнений равновесия. Особенно это касается систем со связями (например, системы тел, соединенные нитями и блоками), состоящих из множества тел
Принцип возможных перемещений.
Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.
Возможное перемещение системы – это малое перемещение, при котором не нарушаются связи, наложенные на систему.
Общее уравнение динамики (принцип Даламбера — Лагранжа)
Принцип Даламбера — Лагранжа – это объединение принципа Даламбера с принципом возможных перемещений. То есть, при решении задачи динамики, мы вводим силы инерции и сводим задачу к задаче статики, которую решаем с помощью принципа возможных перемещений.
Принцип Даламбера — Лагранжа.
При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы равна нулю:
.
Это уравнение называют общим уравнением динамики.
Уравнения Лагранжа
Число обобщенных координат n совпадает с числом степеней свободы системы.
Если, при возможном перемещении системы, изменяются все координаты, то работа, совершаемая внешними силами при таком перемещении, имеет вид:
δA = Q 1 δq 1 + Q 2 δq 2 + . + Qn δqn .
Тогда обобщенные силы являются частными производными от работы по перемещениям:
.
Для потенциальных сил с потенциалом Π ,
.
Уравнения Лагранжа – это уравнения движения механической системы в обобщенных координатах:
Здесь T – кинетическая энергия. Она является функцией от обобщенных координат, скоростей и, возможно, времени. Поэтому ее частная производная также является функцией от обобщенных координат, скоростей и времени. Далее нужно учесть, что координаты и скорости являются функциями от времени. Поэтому для нахождения полной производной по времени нужно применить правило дифференцирования сложной функции:
.
Использованная литература:
А. П. Маркеев, Теоретическая механика, «Ижевская республиканская типография», 1999.
Н. Н. Никитин, Курс теоретической механики, «Высшая школа», 1990.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.
А. А. Яблонский, Курс теоретической механики, часть 2, динамика «Высшая школа», 1986.
Автор: Олег Одинцов . Опубликовано: 20-07-2015 Изменено: 23-08-2019
Принцип виртуальных перемещений в теоретической механике
Содержание:
Принцип Д’аламбера и принцип виртуальных перемещений
Силой инерции материальной частицы называют геометрическую сумму сил Противодействия движущейся материальной частицы телам, сообщающим ей ускорение
Сила инерции
Если в задаче динамики или статики требуется определить движение или условия равновесия какого-либо материального объекта, то, составляя уравнения движения или равновесия этого материального объекта, мы включаем в них только те силы, которые на него реально действуют. В эти уравнения не должны входить силы, с которыми данное тело действует на окружающие материальные тела.
Однако в динамике есть и такой метод решения задач, где наряду с силами, приложенными к данному объекту и сообщающими этому объекту ускорение, учитывают также и силы, с которыми данный объект противодействует телам, сообщающим ему ускорение.
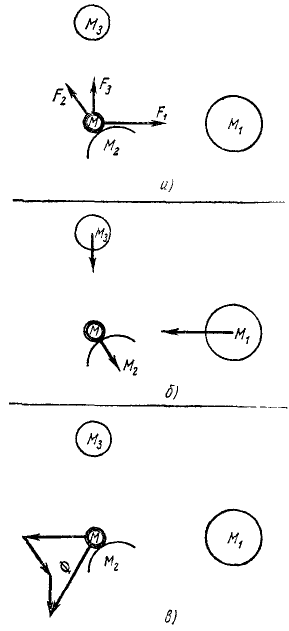
Пусть имеется некоторая материальная частица M (рис. 224, а) и другие материальные объекты M1, M2, M3, . действие которых на данную материальную частицу M представлено силами
Материальная частица M противодействует телам M1, M2, M3, . . Силы противодействия равны силам
Приложим (совершенно условна) эти силы противодействия не к телам M1, M2, M3 . к которым они приложены в действительности, а к материальной частице M и сложим их (рис. 224, в). Эту геометрическую сумму сил противодействия движущейся материальной частицы M телам M1, M2, M3, . сообщающим ей ускорение, называют силой инерции. Мы будем обозначать ее буквой Ф.
Понятие «сила инерции» нельзя отождествлять с уже знакомым нам понятием «инерция». Еще Лазар Карно, первый определивший (1803 г.) силу инерции как силу, «которую тело сообщает всем другим телам, стремящимся вывести его из данного состояния», указывал, что «сила инерции»—величина, вводимая в вычисления наравне с другими силами, тогда как «инерция»—это проявление присущего материи свойства сохранять движение без действия сил.
Сила инерции материальной частицы выражается произведением массы частицы на ее ускорение и направлена противоположно ускорению
Силы инерции широко применяют в науке и технике при различных расчетах, о чем будет сказано в дальнейшем, а сейчас определим величину, направление и размерность силы инерции. Ускорение а, получаемое частицей M под действием сил 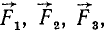
Составляющие силы, геометрическая сумма которых является силой инерции, равны, но противоположны силам 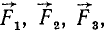
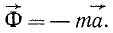
Как видно из этого равенства, размерность силы инерции Ф есть размерность обычных ускоряющих сил, т. е. в физической системе единиц:
[Φ]ф = L 1 M 1 T -2
и в технической системе единиц:
Единицей силы инерции в технической системе единиц могут служить килограмм-сила или его дробные и кратные единицы, а в СИ — ньютон (н).
Касательной силой инерции называют составляющую силы инерции, направленную по касательной к траектории частицы и равную произведению массы частицы на ее касательное ускорение с обратным знаком:
Составляющие силы инерции
В различных задачах динамики, в которых применяют силы инерции, эти силы приходится проецировать на оси и раскладывать по различным направлениям, причем особенно часто по направлениям касательной и главной нормали. Так как сила инерции противоположна ускорению частицы, то и направляющие косинусы силы инерции по величине равны, а по знаку противоположны направляющим косинусам ускорения, и компонента силы инерции по касательной к траектории точки M равна
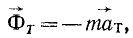
или по абсолютной величине
Эту компоненту называют касательной силой инерции. Как видно из полученного равенства, касательная сила инерции частицы равна произведению массы частицы на ее касательное ускорение и направлена в сторону, противоположную касательному ускорению, т. е. против скорости при ускоренном движении и по скорости — при замедленном.
Нормальной силой инерции называют составляющую силы инерции, направленную по главной нормали к траектории частицы и равную произведению массы на ее нормальное ускорение с обратным знаком:
Компоненту силы инерции, направленную по главной нормали к траектории частицы, называют нормальной силой инерции материальной частицы:
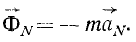
По абсолютной величине
Как видно из (250), нормальная сила инерции частицы равна произведению ее массы на нормальное ускорение и направлена против нормального ускорения, т. е. всегда в сторону выпуклости траектории. Нормальную силу инерции частицы вращающегося тела
называют центробежной силой.
Касательную и нормальную силы инерции можно рассматривать как проекции силы инерции Ф на касательную и на главную нормаль. В таком случае они являются скалярными величинами, как всякие проекции силы на ось.
Если ко всем действующим на точку силам добавить силу инерции, то систему действующих на точку сил можно считать на данное мгновение уравновешенной и применять к ней законы статики
Принцип Д’Аламбера для одной материальной точки
Изложим принцип Д’Аламбера сначала для одной материальной точки, а потом распространим его на механическую систему. Согласно основному уравнению статики точка находится в состоянии равновесия, если сумма всех действующих на точку активных и реактивных сил равна нулю:
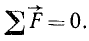
Основным уравнением динамики является
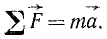
Пусть некоторая точка M массы т под действием всех приложенных к ней активных сил и реакций связи получила ускорение а. Будем считать, что к точке M приложена также и сила инерции Ф.
Тогда, сложив почленно равенства (123′) с равенством (248), получим
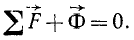
Уравнение динамики переходит в уравнение статики, если ко всем действующим на точку активным силам и силам реакций связей прибавить еще и силу инерции Ф, а следовательно, при этом условии задачу динамики можно решать методами статики. В этом заключается принцип Д’Аламбера.
Если спроецировать все приложенные к точке силы (включая и силу инерции) на оси координат, то принцип Д’Аламбера можно записать в такой форме:
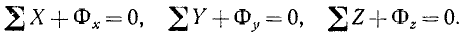
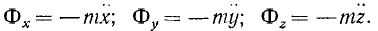
Обозначим через 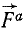
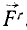
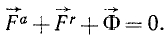
Если к каждой точке материальной системы приложить силу инерции, то систему можно считать на данное мгновение находящейся в равновесии и применять к вей уравнения статики
Принцип Д’Аламбера для системы материальных точек
Пусть на материальные частицы системы действуют активные силы и реакции связей. Приложим к каждой частице системы силу инерции, равную произведению массы частицы на ее ускорение, но направленную против ускорения частицы. Тогда для каждой частицы можно написать
где 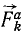
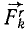
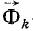
Составив такие уравнения для всех точек системы, мы убедимся, что каждую из этих точек можно считать находящейся в данное мгновение в равновесии. Таким образом, если к каждой точке системы ,приложить силу инерции, то систему можно рассматривать как находящуюся в данное мгновение в равновесии и применять к ней уравнения статики. В этом заключается принцип Д’Аламбера для материальной системы.
Рассматривая только силы инерции, приложенные к какому-либо телу, можно, следуя методу Пуансо, привести их к одной точке, заменить их главным вектором сил инерции и главным моментом сил инерции относительно этой точки и т.п., как это делают в в статике.
Сила инерции не действует на данную массу, но действует на тела, осуществляющие связь
При определении силы инерции материальной частицы M мы мысленно приложили к ней силы действия (или противодействия) этой частицы на другие материальные тела, сообщающие ей ускорение, и геометрическую сумму этих сил назвали силой инерции частицы М. Но эти силы- в действительности приложены не к частице М, а к окружающим ее телам, среди которых могут быть и тела, осуществляющие связь, наложенную на частицу M (тело M2 на рис. 224). Сила инерции лишь мысленно приложена нами к данной частице М. Если бы с-ила инерции реально действовала на массу, то она реально уравновесила бы все прочие силы, приложенные к этой массе и привела бы массу в равновесие.
Так, например, если бы на нашу планету, движущуюся вокруг Солнца, кроме силы притяжения к Солнцу, реально действовала бы и центробежная сила, равная произведению массы Земли на ее центростремительное ускорение и направленная от Солнца, то обе эти силы (сила притяжения и центробежная сила) взаимно уравновесились бы. Тогда согласно принципу инерции Земля продолжала бы удерживаться в состоянии равномерного прямолинейного движения, пока и поскольку приложенные силы не принудили бы ее изменить это состояние. Но с точки зрения классической механики дело обстоит иначе. На движущуюся Землю действует реальная сила притяжения к Солнцу. Центробежная сила инерции на Землю не действует. Земля обладает скоростью, направленной под углом к прямой, соединяющей ее с Солнцем. Сила притяжения к Солнцу сообщает Земле ускорение, направленное по силе. Нормальное ускорение изменяет направление скорости Земли, и Земля описывает эллипс, находясь под действием лишь одной силы притяжения к Солнцу.
Сила, с которой Земля притягивается к Солнцу, приложена к Земле. Равная и обратная сила приложена к Солнцу. Других сил в этой системе двух свободных тел нет. Применяя к Земле любое уравнение динамики, мы должны учитывать лишь одну реально действующую на Землю силу тяготения к Солнцу. Только в случае, если мы желаем применить уравнения статики, рассматривать Землю как находящуюся в данное мгновение в равновесии, только применяя принцип Д’Аламбера или принцип виртуальных перемещений (см. §51), мы мысленно прикладываем к Земле силу, действующую на Солнце, и называем ее силой инерции Земли.
Динамической реакцией связи называют реакцию связи, вызванную действием сил инерции
Динамические реакции
Но силы инерции необходимо учитывать при определении сил, действующих на связи. Силы инерции изменяют реакции связей, и в телах, осуществляющих связь, производят такие же явления, как и прочие известные нам силы, деформируют эти тела, вызывают в них внутренние напряжения и могут даже разрушить.
Рассмотрим пример, внешне очень похожий на предыдущий. Грузик, весом которого пренебрегаем, закрутили на нитке, другой конец которой держат в руке, грузик движется по окружности с постоянной скоростью. На грузик действует единственная сила — натяжение нитки, направленная от грузика к руке. Эта единственная сила выводит грузик из присущего ему, по свойству инерции, равномерного и прямолинейного движения, сообщает грузику нормальное ускорение. Противодействие этой силы приложено к нитке, натягивает ее с силой, равной силе инерции груза.
Реакции связи, вызванные силами инерции, называют динамическими реакциями. При решении следующих задач покажем применение принципа Д’Аламбера к определению динамических реакций.
Задача №1
Ускорение скоростного лифта высотного здания при подъеме изменяется в пределах от +2 м/сек 2 до —2 м/сек 2 . Определить натяжение троса, если вес кабины с пассажирами 1200 кГ.
Решение. Задачу решаем методом Д’Аламбера в СИ. Натяжение троса происходит от веса G= 1200 кГ (статическая нагрузка) и от силы инерции Ф (динамическая нагрузка). К действующим на кабину лифта силам (вес G = m∙g = 11 772 н и натяжение T троса) мысленно прикладываем силу инерции 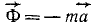
Если лифт поднимается ускоренно, то ускорение направлено вверх, а сила инерции — вниз:
откуда, считая ускорение максимальным,
Если лифт поднимается замедленно, то ускорение направлено вниз, а сила инерции — вверх:
Сила инерции реальна для троса (для связи), так как она меняет его натяжеиие. На кабину лифта сила инерции не действует, так как не приводит ее ни в состояние покоя, ни в равномерное прямолинейное движение.
Ответ. Tmax= 14 172 н = 1445 κΓ; Tmin = 9372 н = 955 кГ.
Задача №2
Вагон совершает вертикальные гармонические колебания по закону у=0,4 sin 10 πt (вибрация). Колебания происходят на рессорах, расположенных между кузовом вагона, весящим 20 Т, и его тележкой, весящей вместе с колесами 2 Т. Определить давления на рельсы.
Решение. Задачу будем решать, применяя принцип Д’Аламбера. Единицами измерения примем L в м, F в T и Т в сек. На вагон действуют следующие силы: вес (кузова и тележки) 22 T и реакция рельсов R.
Определяем силу инерции:
Экстремальные значения силы инерции получим, положив sin 10πt= ± 1. Сокращая π 2 = 9,86 и g =9,81, определим
Нагрузка на рельсы складывается из статической (вес кузова и тележки) и динамической (силы инерции кузова). Давление вагона на рельсы найдем из условия равновесия всех сил (включая и силу инерции), действующих на вагон:
Ответ. Максимальное давление 30 T; минимальное давление 14 Т.
Сила инерции действует на рельсы, так как изменяет давление вагона на рельсы. Сила инерции не действует на вагон, так как не приводит его в состояние равновесия.
Задача №3
Автомобиль весом 1000 кГ движется по выпуклому мосту со скоростью υ =10 м/сек; радиус кривизны в середине моста р=50 м. Определить давление автомобиля на мост в мгновение прохождения его через середину моста.
Решение. Рассмотрим автомобиль, движущийся по мосту (рис. 225).
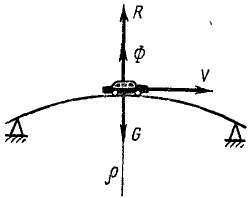
Рис. 225
На автомобиль действуют его вес G = 1000 кГ и реакция моста R. Эти силы не уравновешивают друг друга, так как автомобиль не находится в равновесии. К этим действующим на автомобиль силам приложим мысленно еще силу инерции, равную массе автомобиля, умноженной на ускорение. Автомобиль движется равномерно по криволинейной траектории, поэтому он имеет центростремительное ускорение. Нормальная сила инерции
Силу инерции прикладываем к автомобилю, направляем ее вверх, против нормального ускорения. (В формулах сил инерции знак «—» показывает, что сила инерции направлена против ускорения). Дав такое направление силе (в данном случае вверх), мы тем самым учитываем знак минус и в дальнейшем считаем силу положительной.
После того как сила инерции прибавлена, система сил как бы находится в равновесии, и мы можем применять к пей уравнения статики. Составим сумму проекций сил на вертикальную ось:
Заметим, что сила инерции реально действует на связь (в данном случае на мост) и не действует на движущуюся точку (в данном случае на автомобиль), к которой мы ее прикладываем. Сила инерции реальна для моста, так как давление на мост действительно меньше статического на величину силы инерции. Сила инерции не действует на автомобиль, так как в таком случае он находился бы под действием уравновешенной системы сил и двигался бы равномерно и прямолинейно.
Ответ. R = 796 кГ.
Задача №4
Определить, с какой скоростью должен двигаться искусственный спутник Земли на высоте h = 900 км, если орбиту спутника принять за окружность с центром в центре Земли. Радиус Земли R = 6370 км. Ускорение тела, свободно падающего у поверхности Земли, g =9,81 м/сек 2 . Сила притяжения спутника обратно пропорциональна квадрату расстояния спутника от центра Земли. Спутник считать точечной массой.
Решение. На спутник действует сила притяжения, направленная к центру Земли,
где m— масса спутника, μ-коэффициент, найденный при решении задачи № 155, μ=gR 2 . Следовательно, сила притяжения, действующая на спутник,
Эта сила сообщает спутнику нормальное ускорение, направленное к центру Земли,
Приложим мысленно к спутнику центробежную силу инерции ФN, равную mαN и направленную противоположно центростремительному ускорению. По принципу Д’Аламбера, эта сила уравновешивает единственную действующую на спутник силу F. А по аксиоме статики две взаимно уравновешивающиеся силы по величине равны. Следовательно,
откуда находим скорость спутника:
Ответ. υ = 7,4 км/сек.
Задача №5
Бревно AB длиной l опирается концом А на горизонтальную дорогу AE; другой конец его В привязан веревкой BD длиной d в точке D к грузовику, движущемуся равноускоренно по прямолинейному горизонтальному участку пути, причем высота ED=h. Пренебрегая поперечными размерами бревна, найти, при каком ускорении а грузовика веревка и бревно составляют одну прямую (рис. 226).
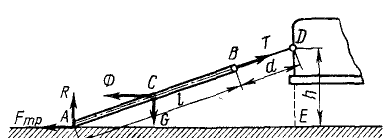
Рис. 226
Решение. На бревно действуют следующие силы: вес G=mg, приложенный в середине бревна С; натяжение веревки Т, приложенное в точке В и направленное к точке D; реакция R, приложенная в точке А и направленная вертикально вверх; сила трения FTp, приложенная к бревну в точке А и направленная горизонтально влево. Прикладываем к бревну силу инерции Ф. Эту силу прикладываем в центре инерции C бревна и направляем против ускорения, т. е. горизонтально влево. По величине эта сила равна m . а. Сила инерции уравновешивает всю .систему сил, и мы вправе применять уравнения статики. Составляем сумму моментов всех сил относительно точки А:
Как видно из чертежа:
Подставляя в предыдущее равенство, определим ускорение. Ответ.
При таком ускорении автомобиля давление бревна на дорогу, а следовательно, и сила трения равнялись бы нулю.
Силы инерции вращающегося звена
Задача №6
Определить величину, направление и точку приложения равнодействующей всех сил инерции звена, вращающегося вокруг неподвижной оси О при следующих данных: масса звена m, момент инерции относительно оси вращения J, расстояние центра масс C от оси вращения ОС = с, угловая скорость в данное мгновение ω, угловое ускорение ε.
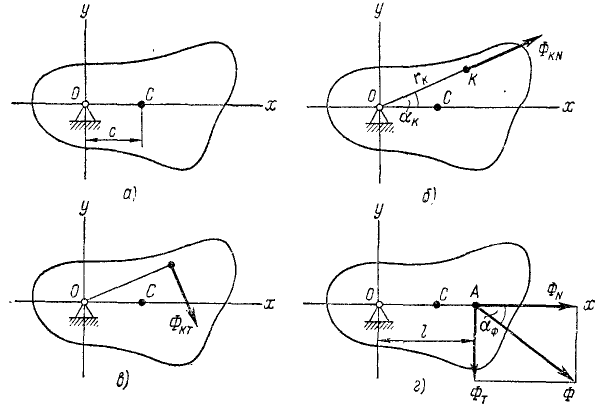
Рис. 227
Решение. Построим систему координатных осей хОу (рис. 227, а) с началом на оси вращения, направив ось Ox к центру масс звена, тогда координаты центра масс:
где mk— масса материальной частицы, a xk и yk—ее координаты, и суммирование распространено на все материальные частицы звена.
К каждой материальной частице звена мысленно приложены центробежная сила инерции и касательная сила инерции. Требуется найти равнодействующую этих сил.
Займемся сначала центробежными силами. Если радиус-вектор k-й частицы обозначим 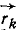
Центробежная сила направлена обратно центростремительному ускорению (от оси вращения О звена), следовательно, центробежные силы всех частиц плоского звена представляют собой плоский пучок сил, пересекающихся в точке О.
Равнодействующая ФN этого пучка (центробежная сила звена) Приложена в той же точке О, проекции этой силы:
Следовательно, центробежная сила звена направлена по оси Ох, т. е. от осн вращения звена к центру масс, и равна произведению массы звена на центростремительное ускорение центра масс:
Перейдем теперь к касательным силам инерции (рис. 227, в). Касательная сила инерции элементарной частицы равна произведению массы этой частицы на ее касательное ускорение и направлена против ускорения:
Проекции этой силы на оси координат:
Линии действия касательных сил инерции различных частиц не пересекаются в точке О, и, чтобы сложить эти силы, надо, следуя методу Пуансо, перенести их к точке О, добавив соответствующие пары, моменты которых равны моментам данных сил относительно точки приведения.
Момент касательной силы инерции, приложенной к k-й точке относительно начала координат О, подсчитаем по формуле (28):
Проекции главного вектора касательных сил инерции:
Следовательно, главный вектор касательных сил инерции равен (по модулю) произведению массы звена на тангенциальное ускорение центра масс звена:
Но этот главный вектор не является равнодействующей касательных сил инерции, так как при перенесении этих сил появился главный момент касательных сил инерции относительно точки приведения, равный алгебраической сумме моментов тангенциальных сил инерции всех частиц звена:
Итак, главный момент касательных сил инерции звена относительно оси вращения равен взятому с обратным знаком произведению момента инерции на угловое ускорение.
Представим главный момент в виде пары, силы которой равны главному вектору, а плечо l равно отношению главного момента к главному вектору:
Мы получили знакомое нам выражение (199) приведенной длины физического маятника.
Одна из сил пары уравновешивается главным вектором Φгл. Т касательных сил инерции, и остается равнодействующая касательных сил инерции, которая равна произведению массы звена на касательное ускорение центра масс, но приложена в центре качания А звена.
Перенесем в центр качания А по линии действия центробежную силу 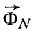
Определим модуль равнодействующей:
и по (6) определим направляющие косинусы:
Ответ. Сила инерции равна произведению массы звена на ускорение центра масс, направлена против ускорения центра масс, но приложена не в центре масс, а в центре качания.
Задача №7
Решить задачу, применив для системы принцип Д’Аламбера.
Решение. Рассмотрим вращение первого вала вокруг оси I — I. На вал действуют вращающий момент M1=50 кГ и момент сопротивления второго вала —Fr1. Добавим момент сил инерции, который равен М (Ф) =—J1ε1.
Рассмотрим вращение второго вала вокруг оси II—II. На него действуют момент со стороны первого вала Fr2. Добавим момент сил инерции —J2ε2. Имеем
Определим отсюда F и подставим в предыдущее уравнение:
Но 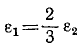
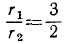
Теперь, когда угловое ускорение второго вала определено, легко вычислить по формулам (87) равноускоренного вращения время, в течение которого вал разовьет угловую скорость ω2 = 4π и число оборотов за это время.
Ответ. n’ — 2,344 оборота.
Задача №8
Стержень длины 2h (рис. 228, а), на концах которого находятся грузы K1 и K2 равного веса (P1 = P2=P) вращается равномерно с угловой скоростью ω вокруг вертикальной оси ACS, проходящей через середину C длины стержня. Расстояние точки C от подпятника АС =а, от подшипника BC = b, AB = a+b=l. Угол между стержнем и осью вращения AB сохраняет постоянную величину а. Пренебрегая весом стержня и размерами грузов, определить проекции давлений на опоры Л и В в тот момент, когда стержень находится в плоскости Ayz.
Решение. Вращающаяся механическая система (твердое тело) состоит из двух точек: K1 с координатами x1=0, y1=-h sinα, z1=a — h cos a и K2 с координатами x2=0, y2= +h sinα, z2= + a + h cos a . На систему (рис. 228,6) действуют внешние силы: веса точек P1 = Р2 = P и реакции в опорах, которые мы проецируем на оси координат. Задачу решим двумя способами: 1) с применением общих уравнений динамики и 2) с применением принципа Д’Аламбера.
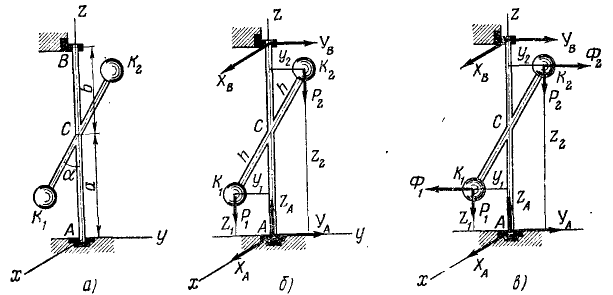
Рис. 228
1-й способ. Для решения задачи первым из указанных способов выпишем уравнения, полученные нами при решении аналогичной задачи № 149:
Подставим в это уравнения данные для рассматриваемой системы и положим ε = 0:
Решая уравнения, находим проекции реакций:
Проекции давлений на опоры имеют ту же величину, но обратные знаки.
2-й способ. Решим теперь задачу методом Д’Аламбера. К действующим в системе внешним (активным и реактивным) силам прибавим мысленно силы инерции. Тело вращается равномерно, поэтому к точкам мы приложим только центробежные силы инерции (рис. 228, в):
Теперь мы можем рассматривать систему как находящуюся в равновесии. Составим уравнения (42) равновесия пространственной системы сил:
Шестое уравнение равновесия превращается в тождество 0 = 0. Решая уравнения, находим проекции реакций, а затем и проекции давлений.
Рассмотрим в отдельности систему сил инерции.
Главный вектор этой системы равен нулю:
Моменты сил- относительно осей у и z тоже равны нулю. Определим сумму моментов центробежных сил инерции относительно оси х. Момент центробежной силы, приложенной к точке K2, определим по формуле (23):
Аналогично выражается момент силы Φ1:
причем знаки моментов получатся автоматически после подстановки в формулу (23) значений (с их знаками) проекций силы и координат точки приложения силы. Главный момент центробежных сил инерции относительно оси х равен сумме моментов всех центробежных сил:
Поэтому сумму произведений массы каждой материальной частицы тела на две координаты этой частицы в данной прямоугольной системе осей называют центробежным моментом инерции:
Таким образом, система сил инерции приводится к паре сил с моментом
Пара сил инерции уравновешивается парой сил реакции в опорах. Вращающееся тело уравновешено статически (xc = 0; yc = 0), но динамическая неуравновешенность (Jvz ≠ 0) вызывает дополнительные давления на опоры.
Ответ. Проекции давлений на опоры:
Сравним оба способа, которыми мы решили задачу № 180.
При втором способе решения задачи мы применяли метод Д’Аламбера, для чего ко всем фактически действующим на тело активным силам и реакциям мы мысленно добавили силы инерции его точек. Обратим внимание на то, что сила инерции какой-либо точки, например A1 или A2, является силой противодействия, оказываемого этой точкой стержням, с которыми она жестко связана и вращение которых сообщает ей центростремительное ускорение. Противодействие передается на опоры и они воспринимают давления неуравновешенного вращающегося тела. Таким образом, сила противодействия оказывается фактически приложенной к опорам А и В. При решении задачи по методу Д’Аламбера мы условно перенесли это давление к самой движущейся массе, отчего система всех сил. приложенных к вращающемуся телу (фактически или только мысленно), оказалась в равновесии. Написав для этой системы сил шесть уравнений статики, мы решили их и определили реакции в опорах, а следовательно, и давления на опоры.
Решая задачу первым способом, мы учитывали только фактически действующие на тело активные и реактивные силы и составили шесть всеобщих уравнений движения (169) и (192), связывающих проекции этих сил с массами и с проекциями ускорений частиц тела. Силы инерции не входят во всеобщие уравнения движения, так как они не действуют на массы, для описания движения которых написаны эти уравнения, т. е. в данном случае они не действуют на точки тела, вращение которого рассматривается в задаче. Решив уравнения движения, мы определили реакции в опорах, а следовательно, и давления на опоры. Таким образом, мы решили задачу как прямую основную задачу динамики: по данному движению системы мы определили силы, действующие на точки системы.
Во всех уже известных нам теоремах и методах мы учитывали только «эффективные», или «ускоряющие», силы, т. е. активные или реактивные силы, фактически приложенные к материальному объекту, движение которого мы изучали. Силы инерции мы применили впервые лишь в принципе Д’Аламбера. В следующем параграфе мы ознакомимся с принципом виртуальных перемещений, в некоторые уравнения которого также входят силы инерции. При решении задач прочими изложенными в нашем курсе методами силы инерции учитывать не надо.
Принцип виртуальных перемещений. Общее уравнение динамики
Идеальными связями называют связи, при которых сумма виртуальных работ их реакций равна нулю:
Идеальные связи
В уравнения равновесия и во всеобщие уравнения движения наряду с активными силами входят и реакции связей. В этих уравнениях могут быть и неизвестные реакции, часто (особенно в динамике) затрудняющие решения.
Если в связях отсутствует трение, то можно при помощи методов, основанных на принципе виртуальных перемещений, получить уравнения, не содержащие сил связи.
В статике мы пользовались виртуальными перемещениями для определения направления реакций. При отсутствии трения мы направляли реакции перпендикулярно к плоскости виртуальных перемещений и называли такие реакции идеальными.
Сила, перпендикулярная к перемещению, не производит работы. Поэтому работа идеальной реакции при виртуальном перемещении равна нулю. Так как существуют связи более сложной природы, выражаемые уравнениями, то указанное свойство принимают как определение и под идеальными связями понимают такие связи, при которых сумма элементарных работ их реакций на всяком виртуальном перемещении системы (или, как говорят, сумма виртуальных работ) равна нулю. Будем считать их связями без трения, стационарными, т. е. не изменяющимися со временем, и удерживающими, т. е. не допускающими таких перемещений, в результате которых точка освобождается от связи.
Виртуальными перемещениями называют воображаемые бесконечно малые перемещения материальной точки или механической системы, допускаемые в данное мгновение наложенными связями без нарушения их
Виртуальные перемещения
Расширим теперь понятие виртуальных («возможных») перемещений, которое нам известно еще со статики. Дадим материальной точке M виртуальное перемещение, т. е. воображаемое бесконечно малое перемещение δr, которое не нарушит связей и произойдет при фиксированном значении t, как бы мгновенно. Тогда координаты точки получат бесконечно малые приращения, называемые изохронными вариациями координат. Это название показывает, что изменения координат происходят при данном значении t. Мы уже встречались с вариациями координат (см. § 38) и обозначили их δx, δy, δz в отличие от обозначений дифференциалов dx, dy, dz, которые выражают действительные бесконечно малые изменения координат точки, происходящие за бесконечно малый промежуток времени dt.
Различие между дифференцированнем и варьированием какой-либо функции f(x, у, z, t) обнаруживается при вычислении бесконечно малых изменений этой функции, получающихся вследствие того, что при дифференцировании время t является переменной величиной, при вариации координат, при виртуальных перемещениях время рассматривают как постоянный параметр. Таким образом,
Из сопоставления этих двух равенств следует, что вариации функции f(x, у, z, t) вычисляют по тому же правилу, что и дифференциал, но при фиксированном значении t. Отсюда становится ясным и различие между воображаемым виртуальным перемещением (происходящим как бы при остановившемся времени) и действительным перемещением (происходящим с течением времени под действием сил и реакций, приложенных к данной точке).
Заметим, что все сказанное здесь о виртуальном перемещении одной точки относится также и к виртуальным перемещениям системы точек.
Работу силы на виртуальном перемещении обозначают δA и иногда коротко называют виртуальной работой.
Если механическая система находится в равновесии, то при любом виртуальном перемещении системы сумма работ всех активных сил равна нулю:
Принцип виртуальных перемещений при равновесии системы
Пусть какая-либо механическая система находится в равновесии, т. е. все точки системы находятся в равновесии под действием активных сил и идеальных реакций. Покажем, что в этой системе сумма элементарных работ всех активных сил на всяком виртуальном перемещении равняется нулю.
Рассмотрим какую-либо одну из точек этой системы. Точка находится в равновесии под действием активных сил (равнодействующую которых обозначим 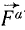
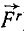
Известно, что работа равнодействующей равна сумме работ составляющих. А так как равнодействующая всех сил, приложенных к взятой нами точке, равна нулю, то, следовательно, равна нулю и сумма элементарных работ всех приложенных к точке активных и реактивных сил, если мы сообщим этой точке какое-либо виртуальное перемещение.
Точку мы выбрали произвольно, и сказанное относится ко всем точкам механической системы.
Дадим теперь механической системе какое-либо виртуальное перемещение. Это перемещение (как всякое виртуальное перемещение) выводит систему из данного положения, но не нарушает связей. Как доказано, сумма работ всех активных сил системы и работ всех идеальных реакций на этом виртуальном перемещении равняется нулю:
Но вторая сумма этого равенства тождественно равняется нулю, потому что связи идеальные, следовательно, равна нулю и первая сумма:
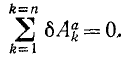
Это равенство выражает принцип виртуальных перемещений: для того чтобы механическая система в некотором положении находилась в равновесии, необходимо, чтобы при любом виртуальном перемещении сумма элементарных работ всех активных сил равнялась нулю.
При решении задач статики по принципу виртуальных перемещений удобно выражать элементарную работу по (221); тогда условие (254) принимает вид
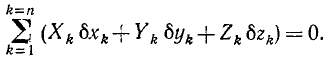
Это уравнение называют общим уравнением статики.
Задача №9
Через две гладкие взаимно перпендикулярные плоскости AB и BC (рис. 229) перекинута тяжелая цепь так. что 100 см цепи лежит на АВ, а остальные 70 см — на ВС. Определить угол ВАС = а, если цепь находится в равновесии.
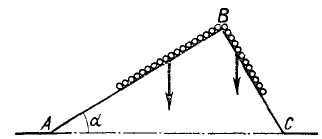
Рис. 229
Решение. Рассмотрим равновесие цепи. На цепь действуют две активные силы: 1) вес 100γ части, расположенной на АВ, н 2) вес 70γ части, расположенной на ВС, где γ—вес единицы длины цепи. Реакции связей нас не интересуют, так как они не входят в уравнение (254). Перемещением, не нарушающим связей, является скольжение цепи (вверх или вниз) по плоскости. Даем системе виртуальное перемещение δs вдоль плоскостей. Сумма элементарных работ сил тяжести на этом перемещении равна нулю, и условие равновесия цепи напишем в следующем виде:
Ответ. tg а = 0,70; а = 35°.
Задача №10
В представленном на чертеже (рис. 230) механизме ABDE — параллелограмм, составленный из стержней, соединенных шарнирами, из которых 4 и E неподвижны. Стержень ABC представляет одно целое. Точка C и ползушка М соединены нитью СМ. В точке В к механизму приложена сила Q, направленная вдоль стержня BD. К ползушке М приложена сила Р, перпендикулярная к BD. Весом частей пренебрегаем. Установить, какова связь между силами P и Q при равновесии.
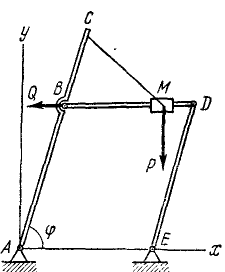
Рис. 230
Решение. Рассматриваем равновесие всего механизма. На механизм действуют активные силы Q и Р. Условие равновесия механизма запишем в Форме общего уравнения (255) статики. Оси координат даны на рисунке. Длина AB = l.
При решении задач по (255) удобно составлять следующую таблицу:
| № | Сила | X | Y | x | y | δx | δy |
| 1 | Q | -Q | 0 | l cos φ | l sin φ | — l sin φ δφ | l cos φ δφ |
| 2 | P | 0 | -P |
Сначала заносим в таблицу все активные силы (2-й столбец), затем в столбцы 3-й и 4-й—их проекции на оси координат, затем в столбцы 5-й и 6-й заносим координаты точек приложения -сил, а в столбцы 7-й и 8-й —вариации этих координат. Если система имеет три измерения, то таблица пополняется соответствующими столбцами для г. Таблица предназначена для решения задачи по уравнению (255), поэтому если в 3-м или 4-м столбцах имеются 0, то заполнять соответствующие строки в столбцах 5, 6, 7 и 8-м излишне.
Внося в (255) данные из таблицы, получим
Ответ.
Сколько выиграно в силе, столько потеряно в скорости
Применение принципа виртуальных перемещений к простейшим машинам
Простейшими машинами здесь названы машины или механизмы с полными связями, т. е. такие, в которых положение всех частей полностью определяется положением одной из точек. Положение всех звеньев такого механизма может быть определено посредством только одного параметра, называемого обобщенной координатой механизма, фиксирующего положение некоторой точки на ее траектории или значение угла поворота звена.
Рассмотрим такой механизм, находящийся под действием двух сил: движущей силы Р, приложенной в точке А, и силы сопротивления R, приложенной в точке В. Сообщим звеньям механизма некоторое бесконечно малое перемещение. Пусть в этом перемещении υA и υB—проекции скоростей точки А на направление силы P и точки В на направление силы R. Тогда получим следующее условие равновесия механизма:
Из этой пропорции видно, что движущая сила и сила сопротивления находятся между собой в отношении, обратном отношению проекций скоростей их точек приложения на направления этих сил.
Это условие выражает золотое правило механики, известное еще древним грекам, оно было сформулировано Тероном, а после Галилеем в следующих словах: сколько выиграно в силе, столько потеряно в скорости.
Если пренебречь трением, то это правило можно приложить ко многим механизмам и простейшим машинам: к рычагам, блокам, полиспастам, зубчатым колесам, различным типам весов, домкратам и т. д. и т. п.
Задача №11
Плоский шарнирный механизм («пантограф») имеет показанное на чертеже устройство (рис. 231). Стержни AD, ВС, . невесомы и образуют ряд ромбов. OK — пружинные весы. Найти, сколько показывают весы, если внизу подвешен груз Q.
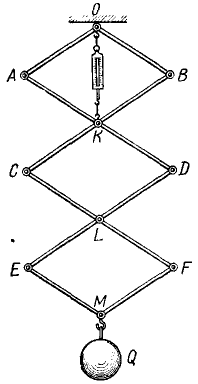
Рис. 231
Решение. Дадим точке M элементарное перемещение δh вниз. Тогда точка K получит перемещение 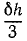
Обозначая силу натяжения пружины (показание весов) через F, составим и приравняем нулю сумму элементарных работ всех активных сил системы:
из этого равенства находим F = 3Q.
Ответ. Показание весов nQ, где n—число ромбов, в данном случае n = 3.
Задача №12
В шарнирном параллелограмме OABC (рис. 232), расположенном в вертикальной плоскости, длина кривошипа 0A = 20 см. Шатун AB весит G = AOh. Пренебрегая весами кривошипов, найти величину момента М, приложенного к кривошипу OA, при условии, что механизм находится в равновесии в указанном на чертеже положении.
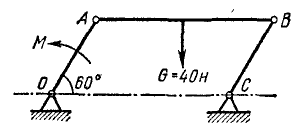
Рис. 232
Решение. Дадим системе виртуальное перемещение, мысленно повернув кривошип OA на угол δφ; тогда, по (223), (224) и (254) Какую горизонтальную силу R надо приложить к правой нижней трубе, чтобы удержать трубы в равновесии? Сила пересекает ось трубы. Радиус сечения труб r, вес каждой трубы Р; линии, соединяющие центры сечений, образуют равнобедренный треугольник с углом α при основании.
Решение. Рассматриваем равновесие системы, состоящей из трех труб. На систему действуют веса труб, приложенные в их центрах тяжести А, В и С, и горизонтальная сила, которую мы переносим (в пределах твердого тела, к которому она приложена) в точку С. Реакции нас не интересуют, так как задачу будем решать, применяя принцип виртуальных перемещений.
Если правой нижней трубе сообщить виртуальное перемещение вдоль оси абсцисс, то виртуальную работу совершат только две силы: сила R, приложенная к нижней трубе в точке С, и вес верхней трубы, приложенный в точке В. Определим проекции этих сил:
Для точек C и B определим нужные нам координаты и их вариации:
Подставляем найденные величины в (255):
Сокращаем на 2r δa и находим ответ.
Ответ.
Задача №13
Верхний конец А однородного бруса AB (рис. 234), длина которого 21, упирается в гладкую вертикальную стену. К нижнему концу В бруса привязана веревка ВС, длина которой 2L, а верхний конец укреплен на стене в точке C- Определить положение равновесия бруса.
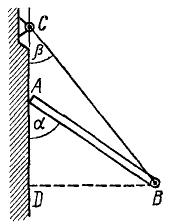
Рис. 234
Решение. На стержень действует только одна активная сила—его собственный вес G. Виртуальным перемещением системы является мысленное малое перемещение точки А вверх или вниз по стене. При этом меняются высота центра тяжести бруса, угол α, составляемый брусом с вертикальной стеной, и угол β между веревкой и вертикальной стеной.
Обозначим через z расстояние по вертикали центра тяжести бруса от точки С. Тогда
z = 2Lcos β-1 cos а.
Находим вариации, считая г, а и β переменными параметрами:
δz = — 2L sin β δβ + l sin α δα.
Работа всех (в данном случае одной) активных сил системы при ее виртуальном перемещении равна нулю:
G δz = G (l sin α δa-2L sin β δβ) = 0.
Но вес бруса пулю не равен, следовательно,
I sin α δa= 2L sin β δβ.
Как видно из чертежа,
BD = 2l sin α = 2L sin β.
Из этого равенства после варьирования находим
21 cos αδα = 2L cos βδβ.
Делим на него равенство, полученное из уравнения равновесия:
Следовательно,
Ответ. AC = AD независимо от угла наклона стержня.
Задача №14
При каком соотношении между весами P1, P2, P3 и Pt грузов А, В, C и D система, изображенная на рис. 235, будет находиться в равновесии? Нить невесома и нерастяжима, трением пренебречь.
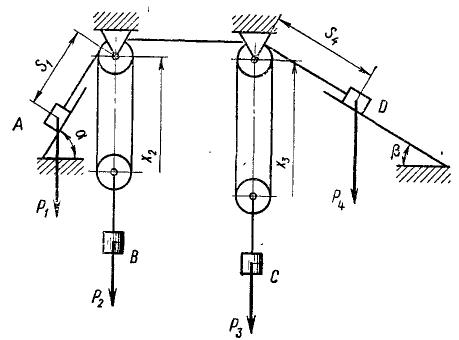
Рис. 235
Решение. Пусть длины s1, x2, x3, s4 определяют положения грузов А, В, C и D. Пусть каждый груз получит виртуальное перемещение. Возьмем сумму виртуальных работ всех активных сил системы, т. е. сил тяжести:
Из условия нерастяжимости нити имеем:
Этим соотношением четыре вариации связаны между собой, а потому только трем из них можно давать независимые друг от друга значения, например трем первым, а четвертая определится из полученного соотношения:
Подставим это значение δs4 в уравнение равновесия:
Вариации δs1, δx2 и δx3 независимые величины и могут принимать различные значения, а потому написанное равенство может тождественно равняться нулю только при условии, что равны нулю все коэффициенты при вариациях. Приравнивая каждую из скобок’нулю, найдем ответ.
Во всякой механической системе с идеальными связями сумма элементарных работ всех активных сил и сил инерции на всяком виртуальном перемещении равна нулю:
Общее уравнение динамики. Если механическая система с идеальными связями не находится в равновесии, то, приложив к каждой точке силы инерции, мы можем согласно принципу Д’Аламбера рассматривать эту систему как находящуюся в данное мгновение в равновесии и применять к ней все уравнения статики и, в частности, уравнение (254).
В самом деле, для каждой точки системы
Но если равна нулю равнодействующая всех активных сил, реакций связей и сил инерции, приложенных к каждой точке, то равна нулю и сумма элементарных работ всех сил, приложенных к каждой точке, а потому равна нулю и сумма элементарных работ всех сил системы:
Если связи системы идеальные, то сумма работ реакций связей на всяком виртуальном перемещении тождественно равняется нулю и в написанном равенстве средняя сумма отпадает:
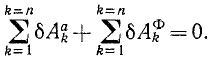
Следовательно, во всякой системе с идеальными связями на всяком виртуальном перемещении сумма работ всех активных сил и всех сил инерции равна нулю. В частном случае, если система находится в равновесии, силы инерции системы равны нулю, и мы получаем (254).
Это уравнение (256) обычно пишут в так называемой аналитической форме, в которой оно особенно удобно при различных применениях. Обозначая проекции активных сил системы на оси координат Xk, Yk и Zk, представляя проекции сил инерции каждой частицы как произведение массы частицы на проекции ускорения с обратным знаком (—mkxk, —mkyk и —mkzk) и обозначая через δxk, δyk и δzk проекции виртуальных перемещений, мы можем выразить элементарные работы по (221), тогда получим
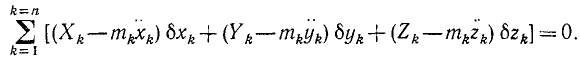
Уравнение (257) называют общим уравнением динамики системы с идеальными связями.
Задача №15
Центробежный регулятор Уатта (рис. 236, а) вращается вокруг вертикальной оси с постоянной угловой скоростью ω. Определить угол отклонения ручек OA и OB от вертикали, принимая во внимание только вес P каждого из шаров А и В и вес P1 муфты С; все стержни имеют одинаковую длину.
Решение. Составим общее уравнение динамики для центробежного регулятора. К трем действующим на регулятор активным силам (к весу муфты и шаров) добавим еще силы инерции. Регулятор вращается равномерно, и имеются только две силы инерции — центробежные силы шаров. Для решения задачи составим таблицу, аналогичную той, какую мы составили пои решении задачи № 182. Построим координатные оси (рис. 236, б), спроецируем на них силы, найдем координаты точек приложения сил и их вариации.
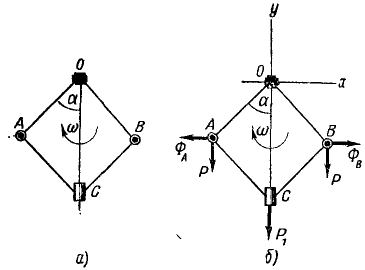
Рис. 236
| № | Сила | X | Y | x | y | δx | δy |
| 1 | PA | 0 | -P | —l cos a | l sin a δa | ||
| 2 | PB | 0 | -P | —l cos a | l sin a δa | ||
| 3 | P1 | 0 | -PI | —2l cos a | 2l sin a δa | ||
| 4 | ФА | 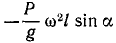 | 0 | —l sin a | —l cos a δa | ||
| 5 | ФВ | 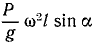 | 0 | l sin a | +l cos a δa |
Найденные значения проекций сил и приращений координат точек их приложения внесем в уравнение (256):
Полагаем, что a ≠ 0, и сокращаем все члены уравнения на 2l sin aδa:
откуда определяем угол отклонения ручек. Ответ.
Для работы регулятора необходимо условие 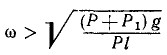
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Аксиомы и теоремы статики
- Система сходящихся сил
- Моменты силы относительно точки и оси
- Теория пар сил
- Определение усилий в стержнях, поддерживающих плиту
- Тело на сферической и стержневых опорах
- Приведение системы сил к простейшему виду
- Плоское движение тела
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://1cov-edu.ru/mehanika/dinamika-tel/
http://www.evkova.org/printsip-virtualnyih-peremeschenij-v-teoreticheskoj-mehanike