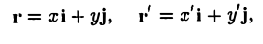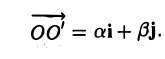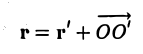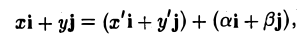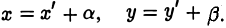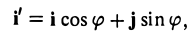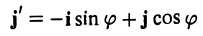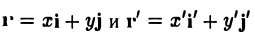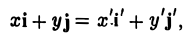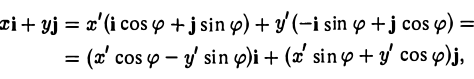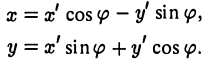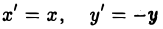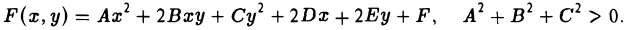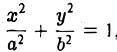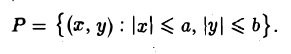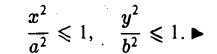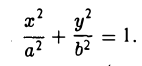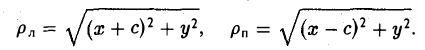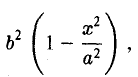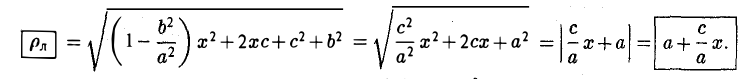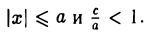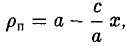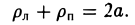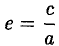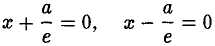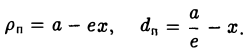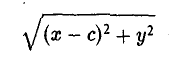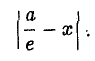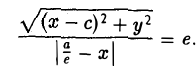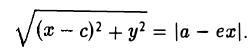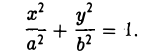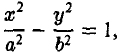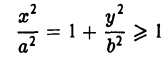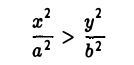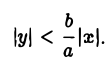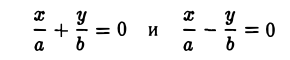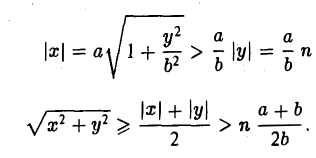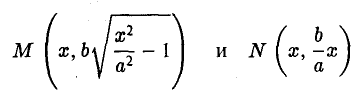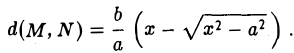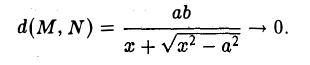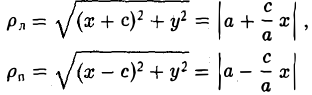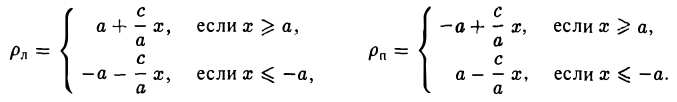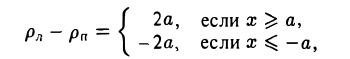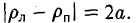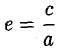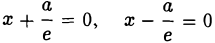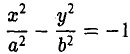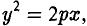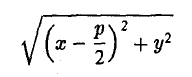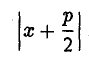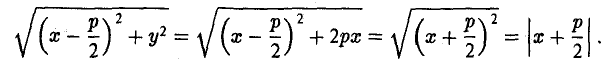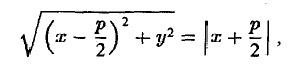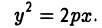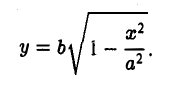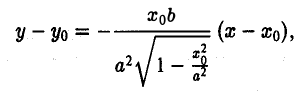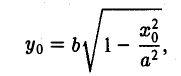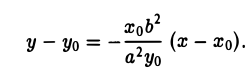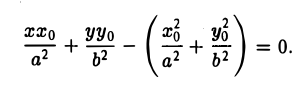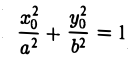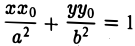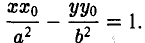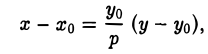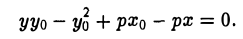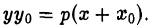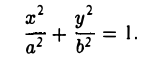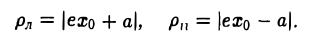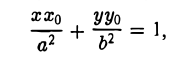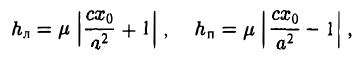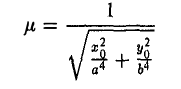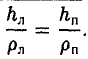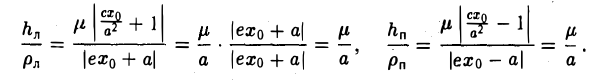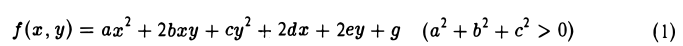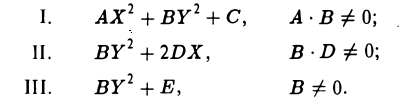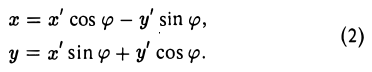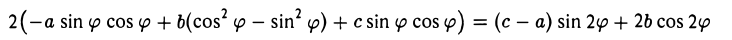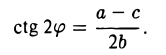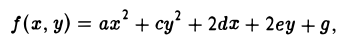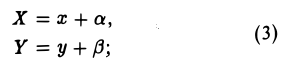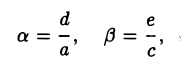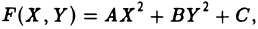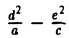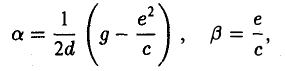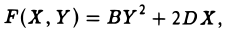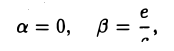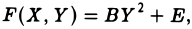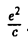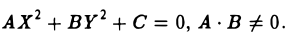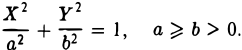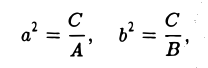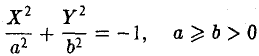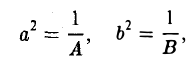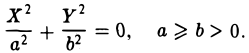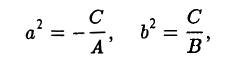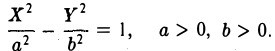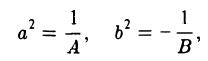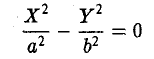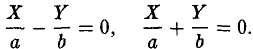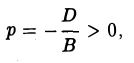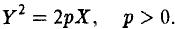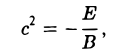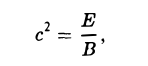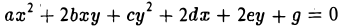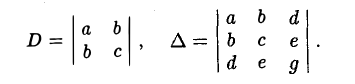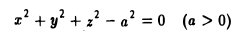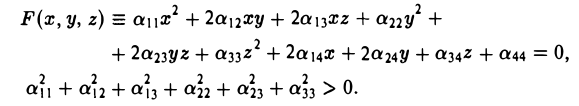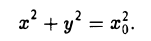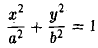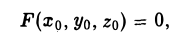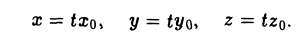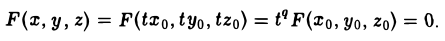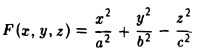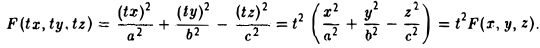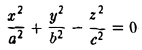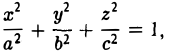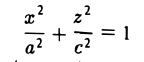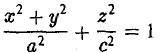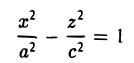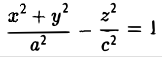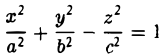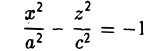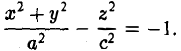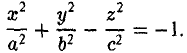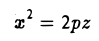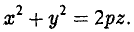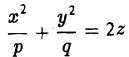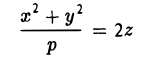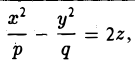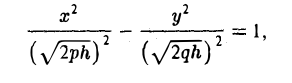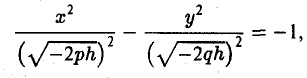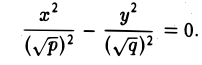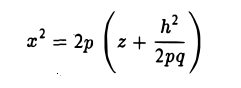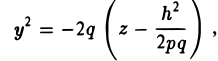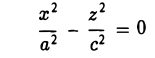Касательная к кривой второго порядка
| Коэффициенты общей кривой второго порядка |
| Точка на кривой, через которую надо провести касательную |
| Заданная формула кривой второго порядка |
| Уравнение касательной в указанной точке |
Касательная к кривой
После того, как мы можем рассчитывать по произвольным координатам ту или иную кривую второго порядка на плоскости по точкам, возникла возможность рассчитать касательную в данной точке этой прямой.
Что же такое касательная? Касательная — это такая прямая которая перескает линию вида
в двух совпадающих точках ( либо целиком входит в состав этой линии)
Выше приведенная формула — есть уравнение кривой второго порядка, а значит при различных заданных коэффициентах, мы можем с помощью этого бота рассчитать уравнение касательной для:
В дальнейшем мы рассмотрим примеры, и Вы сами сможете проверить правильность вычислений.
Уравнение касательной в общем виде выглядит так:
Таким образом, зная все коэффициенты, мы очень легко найдем уравнение касательной в произвольной точке.
Синтаксис
kp2p коэффиценты;координата точки
Где коэффициенты кривой , разделенные как минимум одним пробелом, а координата точки это точка на кривой к которой и надо провести касательную.
Примеры
Вычислить уравнение касательной в точке (3:1) к окружности выраженной формулой
Линия второго порядка, заданная общим уравнением
Пересечение линии второго порядка и прямой.
Рассмотрим линию второго порядка, заданную общим уравнением
$$
Ax^<2>+2Bxy+Cy^<2>+2Dx+2Ey+F=0\label
$$
в декартовой системе координат, и исследуем пересечение этой линии с произвольной прямой
$$
x=x_<0>+\alpha t,\ y=y_<0>+\beta t.\label
$$
Значения параметра \(t\), соответствующие точкам пересечения, должны удовлетворять уравнению, получаемому подстановкой \eqref
$$
A(x_<0>+\alpha t)^<2>+2B(x_<0>+\alpha t)(y_<0>+\beta t)+C(y_<0>+\beta t)^ <2>+\\+ 2D(x_<0>+\alpha t)+2E(y_<0>+\beta t)+F=0.\label
$$
Раскрывая скобки и приводя подобные члены, мы получим уравнение
$$
Pt^<2>+2Qt+R=0,\label
$$
в котором
$$
P=A\alpha^<2>+2B\alpha\beta+C\beta^<2>,\label
$$
$$
Q=(Ax_<0>+By_<0>+D)\alpha+(Bx_<0>+Cy_<0>+E)\beta,\label
$$
или, при другой группировке слагаемых,
$$
Q=(A\alpha+B\beta)x_<0>+(B\alpha+C\beta)y_<0>+D\alpha+E\beta.\label
$$
Свободный член — это значение многочлена при \(t=0\), то есть
$$
R=Ax_<0>^<2>+2Bx_<0>y_<0>+Cy_<0>^<2>+2Dx_<0>+2Ey_<0>+F=0.\label
$$
Вообще говоря, уравнение \eqref
$$
A\alpha^<2>+2B\alpha\beta+C\beta^<2>=0,\label
$$
и, следовательно, уравнение \eqref
В равенство \eqref
Направление, определяемое вектором, компоненты которого удовлетворяют уравнению \eqref
Тип линии.
Выясним, сколько асимптотических направлений может иметь линия второго порядка. Обозначив
$$
\delta=\begin
A& B\\
B& C
\end
$$
сформулируем следующее утверждение.
Линия второго порядка имеет два асимптотических направления, если \(\delta 0\).
Рассмотрим несколько случаев.
- Пусть \(A=C=0\). Тогда \(B \neq 0\) и \(\delta=-B^ <2>0\).
- Случай \(A \neq 0\) исследуется аналогично случаю 2, только нужно рассматривать не угловой коэффициент, а отношение \(\alpha/\beta\).
Поскольку разобранные выше случаи исчерпывают все возможности, предложение доказано.
От противного нетрудно проверить, что и обратно число асимптотических направлений определяет знак \(\delta\).
Мы определили асимптотические направления при помощи аналитического условия \eqref
Используя канонические уравнения, легко проверить, что эллипс не имеет асимптотических направлений, парабола имеет одно, а гипербола — два асимптотических направления (рис. 9.1). Поэтому линии второго порядка называются линиями гиперболического, параболического или эллиптического типа, смотря по тому, имеют они два, одно или не имеют ни одного асимптотического направления.
Для линий гиперболического типа \(\delta 0\).
Рис. 9.1. Асимптотическое направление.
Диаметр линии второго порядка.
Назовем хордой любой отрезок, концы которого лежат на линии, а остальные точки на ней не лежат. Таким образом, хорда не может иметь асимптотического направления.
Предположим, что рассматриваемая линия второго порядка имеет по крайней мере одну хорду. Этому условию удовлетворяют эллипсы, гиперболы, пары пересекающихся прямых, параболы и пары параллельных прямых.
Фиксируем какое-нибудь неасимптотическое направление и исследуем множество середин хорд, имеющих это направление. Если начальная точка \(M_<0>(x_<0>, y_<0>)\) секущей \eqref
$$
(A\alpha+B\beta)x+(B\alpha+C\beta)y+D\alpha+E\beta=0.\label
$$
Рис. 9.2. Хорды.
Прямая \eqref
Стоит обратить внимание на то, что диаметром называется вся прямая. Это не означает, что середины хорд заполняют ее целиком. Так может быть, но возможно также, что множество середин хорд есть, например, отрезок или луч.
Конечно, остается сомнение, действительно ли уравнение \eqref
$$
A\alpha+B\beta=0,\ B\alpha+C\beta=0.\nonumber
$$
Умножим первое из этих равенств на \(\alpha\), второе — на \(\beta\) и сложим. Мы получим равенство \eqref
Центр линии второго порядка.
Обозначим левую часть уравнения \eqref
По-видимому, это определение зависит от выбора системы координат, так как в нем участвует не линия, а многочлен, стоящий в левой части ее уравнения. Допустим, что координаты \(x_<0>, y_<0>\) точки \(O\) в некоторой системе координат удовлетворяют уравнению \eqref
Ниже мы докажем, что в том случае, когда линия содержит хоть одну точку, центры линии и только они являются ее центрами симметрии. Однако понятие центра несколько более общее: линии, являющиеся пустыми множествами, имеют вполне определенные центры, хотя говорить об их центрах симметрии смысла нет. Например, каждая точка прямой \(y=0\) является центром линии с уравнением \(y^<2>+1=0\).
Получим систему уравнений для координат центра. С этой целью напишем подробнее равенство \eqref
$$
A(x_<0>+\alpha)^<2>+2B(x_<0>+\alpha)(y_<0>+\beta) +\\+ C(y_<0>+\beta)^<2>+2D(x_<0>+\alpha)+2E(y_<0>+\beta)+F.\nonumber
$$
Правая часть отличается от левой только знаками у \(\alpha\) и \(\beta\). Поэтому при вычитании \(\boldsymbol<\Phi>(x_<0>-\alpha, y_<0>-\beta)\) из \(\boldsymbol<\Phi>(x_<0>+\alpha, y_<0>+\beta)\) уничтожаются все члены, кроме тех, в которые \(\alpha\) и \(\beta\) входят в первой степени, а члены с первыми степенями удвоятся. После упрощений мы получаем
$$
(Ax_<0>+By_<0>+D)\alpha+(Bx_<0>+Cy_<0>+E)\beta=0.\label
$$
Но равенство \eqref
$$
\left\<\begin
Ax_<0>+By_<0>+D=0,\\
Bx_<0>+Cy_<0>+E=0.
\end
$$
Легко видеть, что и обратно, если справедливы равенства \eqref
Исследуем, обязательно ли существуют центры у линии второго порядка, а если они существуют, то сколько их и как они расположены. Система уравнений \eqref
$$
\delta=\begin
A& B\\
B& C
\end
$$
Таким образом, условие \(\delta \neq 0\) необходимо и достаточно для того, чтобы линия второго порядка имела единственный центр.
Линии второго порядка, имеющие единственный центр, называются центральными.
Полученное условие показывает, что центральными являются линии эллиптического и гиперболического типов.
Условие \(\delta=0\) характеризует нецентральные линии. Это — линии параболического типа. При условии \(\delta=0\) система \eqref
Если линия второго порядка не является пустым множеством и имеет центр \(O(x_<0>, y_<0>)\), то он — ее центр симметрии.
В самом деле, рассмотрим произвольную точку линии \(M(x, y)\) и докажем, что симметричная ей относительно \(O\) точка \(M_<1>(x_<1>, y_<1>)\) также лежит на линии. Точка \(M_<1>\) определяется равенством \(\overrightarrow
Если линия содержит хотя бы одну точку и имеет центр симметрии \(O(x_<0>, y_<0>)\), то \(O\) является центром.
Рассмотрим пересечение линии с прямой, проходящей через \(O\), приняв эту точку за начальную точку прямой. Имеются две возможности:
- Точка \(O\) лежит на линии. Пусть прямая имеет неасимптотическое направление. Тогда \(O\) — единственная точка пересечения, так как иначе с учетом симметрии точек пересечения было бы не меньше трех. Следовательно, уравнение \eqref
имеет кратный корень \(t=0\), откуда вытекает \(Q=0\). Итак, координаты точки \(O\) удовлетворяют равенству (12) при любых \(\alpha\) и \(\beta\), соответствующих неасимптотическим направлениям. Выберем два различных неасимптотических направления \((\alpha, \beta)\) и \((\alpha’, \beta’)\) и рассмотрим равенства
$$
\begin
& (Ax_<0>+By_<0>+D)\alpha+(Bx_<0>+Cy_<0>+E)\beta=0,\\
& (Ax_<0>+By_<0>+D)\alpha’+(Bx_<0>+Cy_<0>+E)\beta’=0.
\end\nonumber
$$
как систему уравнений с коэффициентами \(\alpha\), \(\beta\), \(\alpha’\), \(\beta’\), причем \((\alpha\beta’-\alpha’\beta \neq 0)\). Мы получаем равенства \eqref, как и требовалось. - Точка \(O\) не лежит на линии. Если прямая пересекает линию в точке \(M\), которой соответствует значение параметра \(t_ <1>\neq 0\), то существует симметричная точка пересечения со значением параметра \(-t_<1>\). Тогда \(Pt_<1>^<2>+2Qt_<1>+R=0\) и \(Pt_<1>^<2>-2Qt_<1>+R=0\), откуда следует \(Q=0\).
Таким образом, если линия имеет точки пересечения с двумя различными прямыми, проходящими через \(O\), то, как и выше, мы можем получить равенства \eqref
Сопряженные направления.
Направление \((\alpha’, \beta’)\), определяемое диаметром, сопряженным направлению \((\alpha, \beta)\), называется сопряженным направлению \((\alpha, \beta)\). Компоненты \((\alpha’, \beta’)\), направляющего вектора диаметра \eqref
$$
(A\alpha+B\beta)\alpha’+(B\alpha+C\beta)\beta’=0\label
$$
или
$$
A\alpha\alpha’+B(\alpha’\beta+\alpha\beta’)+C\beta\beta’=0\label
$$
В последнее выражение пары чисел \((\alpha, \beta)\) и \((\alpha’, \beta’)\) входят симметричным образом. Поэтому имеет место следующее утверждение.
Если направление \((\alpha’, \beta’)\), сопряженное с \((\alpha, \beta)\), не является асимптотическим, то сопряженным для \((\alpha’, \beta’)\) будет направление \((\alpha, \beta)\) (рис. 9.3).
Рис. 9.3. Сопряженные направления.
Возникает вопрос, при каких условиях направление, сопряженное какому-нибудь направлению \((\alpha, \beta)\) может оказаться асимптотическим. Это легко выяснить. Из равенства \eqref
$$
A(B\alpha+C\beta)^<2>-2B(B\alpha+C\beta)(A\alpha+B\beta)+C(A\alpha+B\beta)^<2>=0.\nonumber
$$
После преобразований получаем \((AC-B^<2>) \times (A\alpha^<2>+2B\alpha\beta+C\beta^<2>)=0\). Поскольку исходное направление не асимптотическое, это произведение может обратиться в нуль только за счет первого сомножителя. Мы получаем новое утверждение.
Если линия не центральная \((\delta=0)\), то для любого направления \((\alpha, \beta)\) сопряженное направление — асимптотическое (рис. 9.4). Если линия центральная \((\delta \neq 0)\), то направление, сопряженное любому направлению, не асимптотическое.
Рис. 9.4. Сопряженные направления у параболы.
Главные направления.
Если диаметр перпендикулярен хордам, которым он сопряжен, то он является осью симметрии рассматриваемой линии.
Направление \((\alpha, \beta)\) и направление \((\alpha’, \beta’)\) сопряженного ему диаметра называются главными направлениями, если они перпендикулярны.
Если система координат декартова прямоугольная, то для главного направления компоненты \((\alpha, \beta)\) должны быть пропорциональны коэффициентам уравнения \eqref
$$
A\alpha+B\beta=\lambda\alpha,\ B\alpha+C\beta=\lambda\beta.\label
$$
Исключая \(\lambda\), мы получаем уравнение для \(\alpha\) и \(\beta\):
$$
(A-C)\alpha\beta+B(\beta^<2>-\alpha^<2>)=0.\label
$$
Если положить \(\alpha=\cos \varphi\), \(\beta=\sin \varphi\), то уравнение \eqref
Каждая линия второго порядка имеет хотя бы одну пару главных направлений.
Более подробное исследование уравнения \eqref
Касательная к линии второго порядка.
Как известно, касательной к какой-либо линии называется предельное положение секущей, когда хорда стягивается в точку. Выведем уравнение касательной к линии второго порядка, заданной уравнением \eqref
Особой точкой линии второго порядка называется ее центр, который лежит на линии.
Особыми точками являются: точка пересечения пары пересекающихся прямых, единственная точка пары мнимых пересекающихся прямых и каждая точка пары совпавших прямых. В особой точке касательная не определена. Если точка лежит на прямой, входящей в состав линии, то касательная в этой точке совпадает с прямой. Исключив эти случаи, мы фактически ограничиваемся рассмотрением касательных к эллипсам, гиперболам и параболам.
Рассмотрим точку \(M_<0>(x_<0, y_<0>>)\), лежащую на линии \(L\), и прямую с начальной точкой \(M_<0>\), заданную уравнением \eqref
Так как начальная точка принадлежит \(L\), в уравнении \eqref
$$
(Ax_<0>+By_<0>+D)\alpha+(Bx_<0>+Cy_<0>+E)\beta=0.\label
$$
Так как \(M_<0>\) не особая точка, обе скобки здесь одновременно в нуль не обращаются, и условие \eqref
$$
(Ax_<0>+By_<0>+D)(x-x_<0>)+(Bx_<0>+Cy_<0>+E)(y-y_<0>)=0.\label
$$
Это и есть уравнение касательной к линии \(L\) в точке \(M_<0>\), лежащей на линии. Уравнение \eqref
$$
(Ax_<0>+By_<0>+D)x_<0>+(Bx_<0>+Cy_<0>+E)y_<0>+Dx_<0>+Ey_<0>+F=0.\nonumber
$$
Прибавляя это равенство к \eqref
$$
Axx_<0>+B(xy_<0>+x_<0>y)+Cyy_<0>+D(x+x_<0>)+E(y+y_<0>)+F=0.\label
$$
Особые точки.
Напомним, что особая точка линии второго порядка — это ее центр, лежащий на линии. Исследуем, при каких условиях линия второго порядка имеет особую точку. Для координат \((x_<0>, y_<0>)\) особой точки должны быть справедливы равенства
$$
\begin
& Ax_<0>+By_<0>+D=0,\ Bx_<0>+Cy_<0>+E=0,\\
& Ax_<0>^<2>+2Bx_<0>y_<0>+Cy_<0>^<2>+2Dx_<0>+2Ey_<0>+F=0.
\end
$$
Умножим первое из них на \(x_<0>\), второе на \(y_<0>\) и вычтем из третьего. Мы получим эквивалентную систему уравнений
$$
\left\<\begin
Ax_<0>+By_<0>+D=0,\\
Bx_<0>+Cy_<0>+E=0,\\
Dx_<0>+Ey_<0>+F=0.
\end
$$
Выберем какой-нибудь базис в пространстве и рассмотрим вспомогательные векторы \(\boldsymbol
(A, B, D)\), \(\boldsymbol(B, C, E)\) и \(\boldsymbol
$$
x_<0>\boldsymbol
+y_<0>\boldsymbol=-\boldsymbol
$$
Отсюда следует, что при наличии особой точки векторы \(\boldsymbol
\), \(\boldsymbol\) и \(\boldsymbol
$$
\triangle=\begin
A& B& D\\
B& C& E\\
D& E& F
\end
$$
Если линия центральная, то векторы \(\boldsymbol
\) и \(\boldsymbol\) не коллинеарны, и условие компланарности \eqref
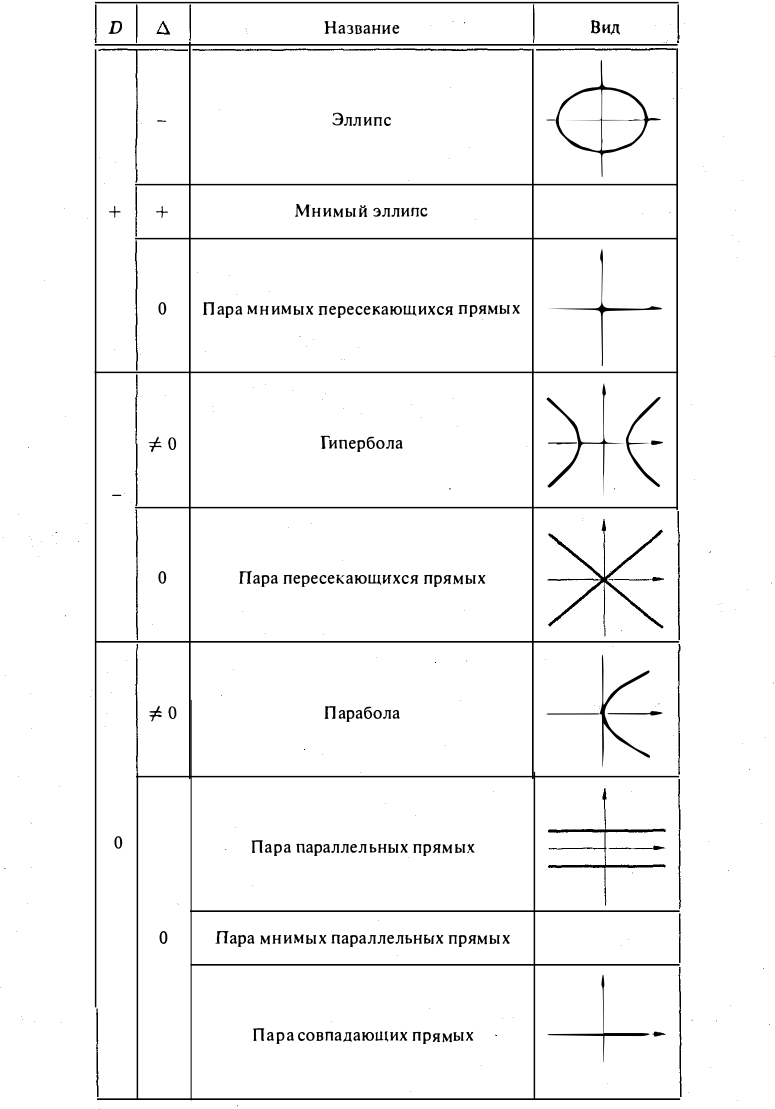
Центральная линия имеет особую точку тогда и только тогда, когда \(\triangle=0\).
Итак, сочетание \(\delta 0\), \(\triangle=0\) — пары мнимых пересекающихся прямых.
Рассмотрим нецентральные линии. Для них существует центр, хотя бы не являющийся особой точкой, тогда и только тогда, когда \(\triangle=0\). В этом (и только этом) случае векторы \(\boldsymbol
\) и \(\boldsymbol\) коллинеарны. Действительно, так как \(\delta=0\), по предложению 9 § 2 гл. II, если система уравнений \eqref
Обратно, пусть для нецентральной линии \(\triangle=0\). Докажем, что \(\boldsymbol
\) и \(\boldsymbol\) коллинеарны, что равносильно совместности уравнений центра. Действительно, в противном случае \(\boldsymbol
\) и \(\boldsymbol\) коллинеарны, и мы получаем противоречие.
Для нецентральных линий условие \(\triangle=0\) равносильно существованию центра.
Итак, сочетание \(\delta=\triangle=0\) характеризует пары параллельных прямых (вещественных, мнимых или совпавших).
Из последних двух утверждений следует, что равенство \(\triangle=0\) является инвариантным: оно не может измениться при переходе к другой системе координат.
Кривые и поверхности второго порядка в математике с примерами решения и образцами выполнения
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида.
Кривые второго порядка используются при решении задач по аналитической геометрии, кривые других порядков используются при решении задач математического анализа в разделе вычисления кратных, криволинейных и поверхностных интегралов.
Кривые и поверхности второго порядка
Преобразование координат на плоскости
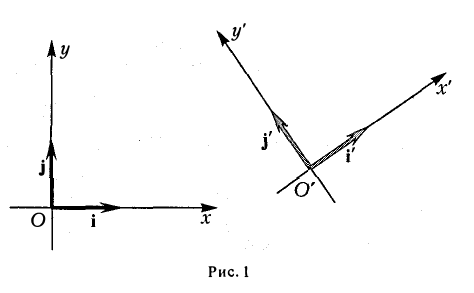
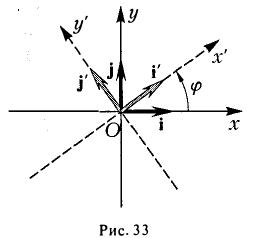
Пусть на плоскости заданы две прямоугольные декартовы системы координат, Оху и О’х’у’ (рис. 1). Произвольная точка М относительно одной из этих координатных систем определяется парой чисел х и у, а относительно другой — парой чисел x’ и у’. Ясно, что между парами (х,у) и (x’, у’) имеется связь. Найдем ее.
Параллельный перенос
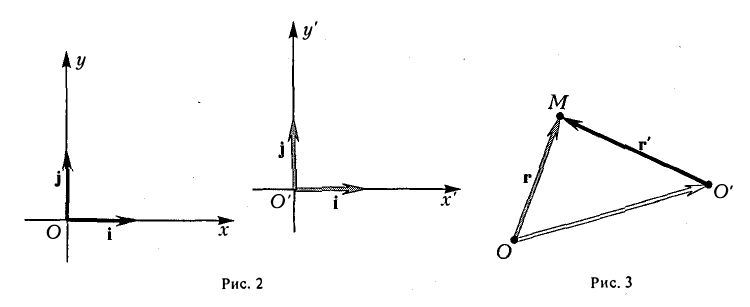
Предположим, что соответствующие координатные оси параллельны и сонаправлены, а точки начала отсчета различны. Это означает, что орты координатных осей соответственно равны (рис. 2).
Пусть г и г’ — радиусы-векторы точки М, т.е.
и а, β — координаты точки О’ относительно системы координат Оху, т. е.
Поворот
Предположим, что координатные оси одной системы координат получаются из координатных осей другой системы поворотом на угол φ, а начальные точки совпадают (рис.4). Координатами единичного вектора i’ являются косинусы углов φ и 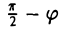
а координатами единичного вектора j’ служат косинусы углов 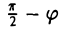
(рис. 5). Так как радиус-векторы
произвольной точки М в рассматриваемом случае равны,
то, заменяя векторы i’ и j’ их выражениями, получаем, что
Зеркальное отражение
В случае, когда оси абсцисс Ох и Ох’ координатных систем совпадают, а оси ординат Оу и Оу’ направлены противоположно, координаты (х, у) и (х’,у’) произвольной точки М связаны равенствами
Справедливо следующее утверждение.
Любое преобразование прямоугольных декартовых координат (с сохранением масштаба) можно представить в виде последовательного выполнения переноса, поворота и <если необходимо) зеркального отражения.
Кривые второго порядка
Пусть на плоскости задана прямоугольная декартова система координат Оху. Множество точек плоскости, координаты х и у которых удовлетворяют равенству
F(x, у) = 0,
где F(x, у) — некоторая функция двух переменных, называется плоской кривой, или плоской линией само равенство называется уравнением данной линии (кривой).
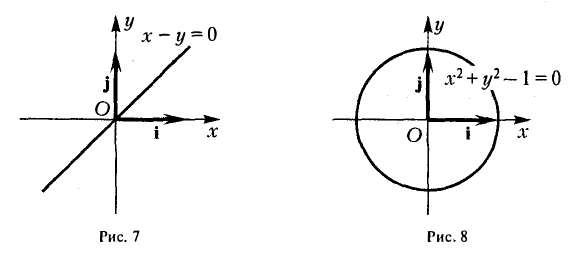
Например, равенство х — у = 0 есть уравнение прямой — биссектрисы первого и третьего координатных углов (рис. 7). Равенство x 2 + y 2 — 1 = 0 — уравнение окружности единичного радиуса с центром в начале координат (рис. 8).
Рассмотрим многочлен второй степени от двух переменных х и у:
F(x,y) = 0
будем называть уравнением линии (кривой) второго порядка.
Если линиями первого порядка являются именно прямые и только они, то множество кривых второго порядка заметно разнообразней. Поэтому исследованию общего уравнения кривой второго порядка естественно предпослать изучение некоторых частных, но важных случаев.
Эллипс
Эллипсом называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение эллипса имеет вид (1), называется канонической (для данного эллипса); само уравнение (!) называется каноническим уравнением эллипса. Окружность
является частным случаем эллипса (при а = b). Это позволяет несложным способом определить форму эллипса: эллипс (1) получается из окружности (2) путем ее равномерного сжатия» к оси Ох (с коэффициентом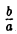
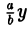
Свойства эллипса
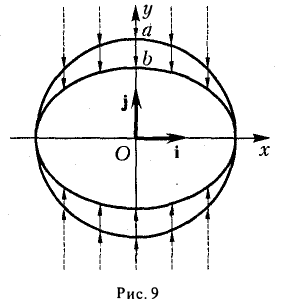
- Эллипс (I) содержится в прямоугольнике
В этом легко убедиться, заметив, что, если точка М(х, у) принадлежит эллипсу (1), то (рис. 10)
Точки (±а, 0), (0, ±b) называются вершинами эллипса.
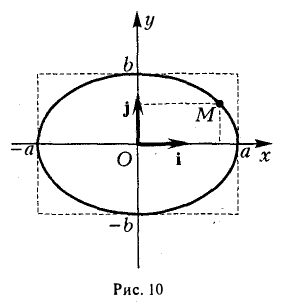
2. Координатные оси Ох и Оу канонической системы являются осями симметрии эллипса, а начало координат О — его центром симметрии. Это означает, что если точка Мо(хo, yо) принадлежит эллипсу, то точки (-хо, yо), (-xо, -yо) и (хо, -yо) также ему принадлежат (рис. 11).
3. Если эллипс не является окружностью, то координатные оси канонической системы — единственные оси симметрии.
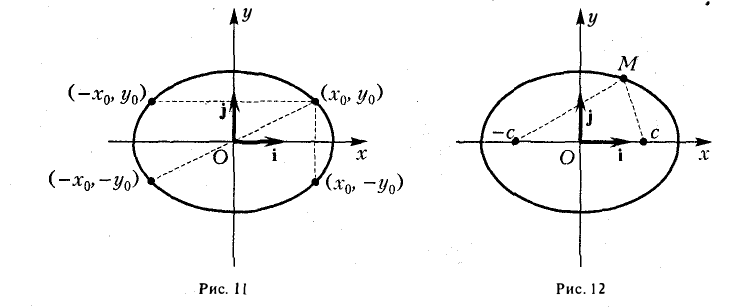
Положим с = 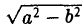
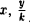
Пусть сначала М(х, у) — произвольная точка эллипса
Вычислим ее расстояния от фокусов эллипса (рис. 12). Имеем
Заменяя y 2 его выражением
после несложных преобразований получаем, что
Последнее равенство вытекает из того, что
Легко убедиться в том, что
Доказательство того, что точки, обладающие указанным свойством, принадлежат эллипсу, было проведено ранее (см. раздел «Простейшие задачи аналитической геометрии» Введения, задача 2).
называется эксцентриситетом эллипса (I). Ясно, что 0
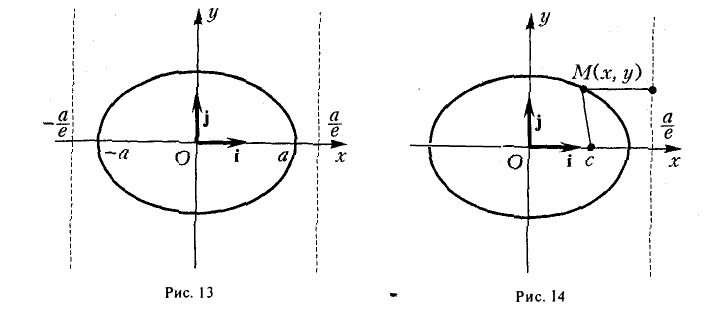
называются директрисами эллипса. У каждого эллипса две директрисы — левая и правая (рис. 13).
5. Эллипс есть множество точек плоскости, отношение расстояний от которых до данной точки (фокуса эллипса) и доданной прямой (одноименной с фокусом директрисы эллипса) постоянно (равно эксцентриситету эллипса).
Пусть сначала М(х,у) — произвольная точка эллипса (1). Вычислим расстояния от нее до правого фокуса и до правой директрисы (рис. 14). Имеем соответственно
Откуда легко получаем требуемое
Аналогично проверяется, что
Рассмотрим теперь на плоскости точку (с, 0) и прямую х =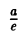
— и до выбранной прямой —
Возведем обе части последнего соотношения в квадрат и, положив 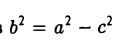
Тем самым, точка М(х,у) лежит на эллипсе (1).
Гипербола
Гиперболой называется кривая, уравнение которой в некоторой прямоугольной системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение гиперболы имеет вид (1), называется канонической (для данной гиперболы); само уравнение (1) называется каноническим уравнением гиперболы.
Свойства гиперболы
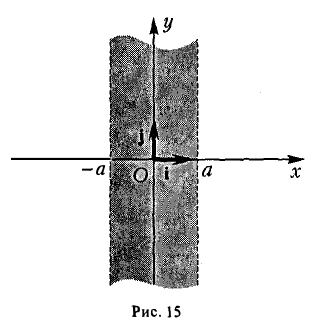
- Гипербола (1) лежит вне полосы |x|
и, значит, |x| ≥ а (рис. 15).
Точки (±а, 0) называются вершинами гиперболы.
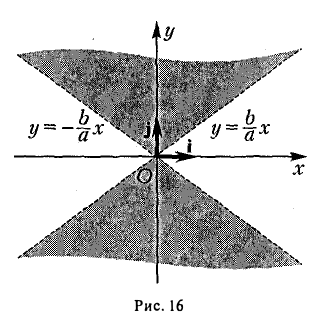
2. Гипербола (1) лежит в вертикальных углах, образованных прямыми у = ±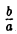
вытекает, что если точка М(х, у) лежит на гиперболе (1), то
Таким образом, гипербола состоит из двух частей — ветвей гиперболы, левой и правой. Прямые
называются асимптотами гиперболы.
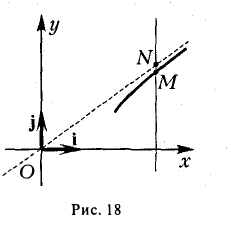
3, На гиперболе лежат точки, сколь угодно далекие от начала координат O(0, 0).
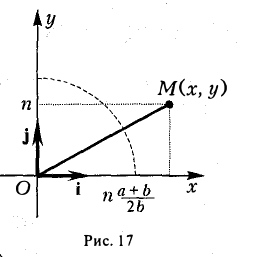
Пусть, например, точка М(х, у) лежит на гиперболе (1) и \у\ = n, где n — произвольное положительное число (рис. 17).
Возьмем в первой четверти две точки: точку гиперболы (1) и точку ее асимптоты 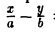
соответственно — и вычислим расстояние между ними. Имеем
Умножив и разделив полученное выражение на сумму х +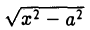
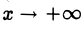
Тем самым, установлен следующий факт.
4. Если текущая точка асимптоты неограниченно удаляется от начала координат, т.е. \х\ —» + ∞, то на гиперболе можно указать соответствующую ей точку так, чтобы расстояние между ними стремилось к нулю (рис. 18).
Верно и обратное.
стремится к нулю.
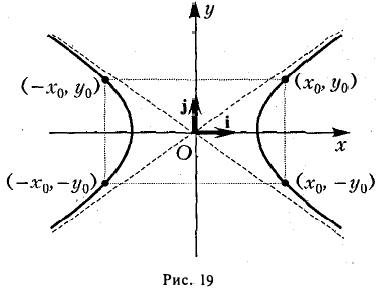
6. Оси канонической координатной системы являются осями симметрии гиперболы, а начало координат — ее центром симметрии (рис. 19).
Координатные оси канонической системы — единственные оси симметрии гиперболы.
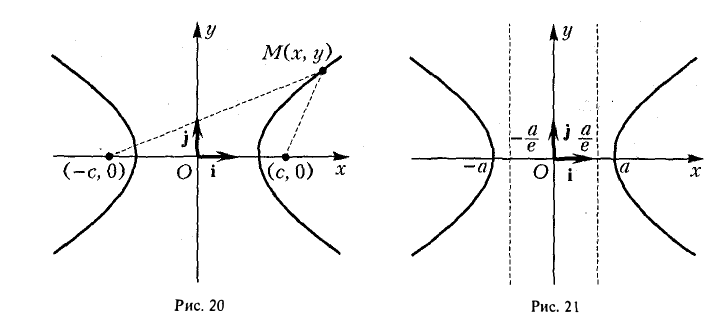
Положим с = 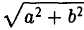
Гипербола есть множество точек, абсолютная величина разности расстояний от которых до двух данных точек (фокусов гиперболы) постоянна (равна заданному числу).
Доказательство этого свойства проводится так же, как и доказательство свойства 4 эллипса. Покажем, например, что каждая точка гиперболы обладает указанным свойством. Если М(х, у) — точка гиперболы (1), то расстояния от нее до фокусов соответственно равны
(рис. 20). Так как 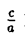
Отсюда нетрудно вычислить, что
называется эксцентриситетом гиперболы (1). Ясно, что е > 1. Прямые
называются директрисами гиперболы (рис. 21). У каждой гиперболы две директрисы — левая и правая.
Практически также, как и для эллипса, доказывается следующий факт.
8. Гипербола есть множество точек, отношение расстояний от которых до данной точки (фокуса гиперболы) и доданной прямой (одноименной с фокусом директрисы) постоянно (равно эксцентриситету гиперболы) (рис. 22).
Гипербола (2)
называется сопряженной гиперболе (1). Взаимное расположение гипербол (1) и (2) указано на рис. 23.
Парабола
Параболой называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение параболы имеет вид (1), называется канонической (для данной параболы); уравнение (]) называется каноническим уравнением параболы.
Свойства параболы
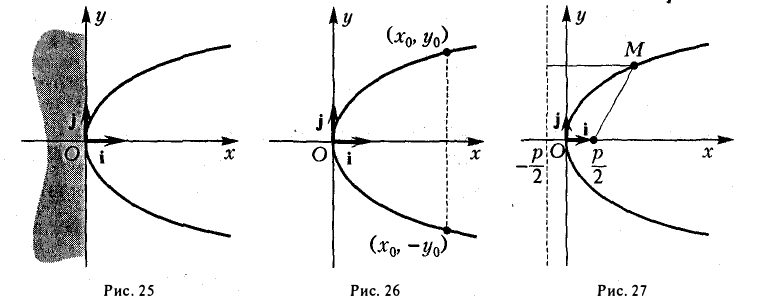
- Все точки параболы лежат в правой полуплоскости: х ≥ 0 (рис. 25). Точка 0(0, 0) лежит на параболе и называется ее вершиной.
- На параболе лежат точки, сколь угодно далеко расположенные от начала координат О(0, 0).
- Ось абсцисс канонической координатной системы является (единственной) осью симметрии параболы (рис. 26).
Ось симметрии параболы называется осью параболы. Число р называется фокальным параметром параболы; точка (

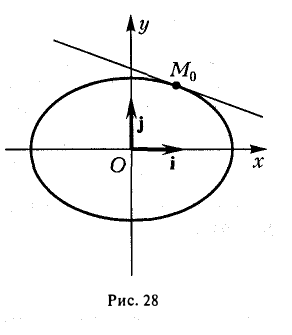
4. Парабола есть множество точек, равноудаленных отданной точки (фокуса параболы) и от данной прямой (директрисы параболы) (рис. 27).
Пусть точка М(х, у) лежит на параболе (1). Вычислим расстояния от нее до фокуса (
и до директрисы х = —
Заменяя у 2 его выражением 2рх, легко убеждаемся в том, что
Верно и обратное. Если для некоторой точки М(х, у) расстояния от нее до точки (

то, возводя в квадрат, после простых преобразований получаем, что эта точка лежит на параболе:
Оптическое свойство кривых второго порядка
Касательные к эллипсу и гиперболе
Если кривая задана уравнением
y = f(x)
то уравнение касательной к ней, проходящей через точку (хо,у0)> где Уо = f(xо), можно записать в следующем виде
Пусть Мо(хо, yо) — точка эллипса
Предположим для определенности, что точка М0 лежит в первой четверти, т. е. хо > 0, yо > 0. Тогда часть эллипса, лежащую в первой четверти, можно описать уравнением
Пользуясь формулой (1), получаем уравнение касательной к эллипсу в точке Мо
а так как точка (х0, у о) лежит на эллипсе, то
Полученное соотношение после несложных преобразований можно записать так:
Отсюда с учетом тождества
приходим к уравнению
(рис. 28). Полученное соотношение является уравнением касательной к эллипсу, проходящей через его точку (х0, yо), и в общем случае ее произвольного расположения, т. е. при любых знаках хо и уо.
Уравнение касательной к гиперболе выводится аналогично и имеет следующий вид
Подчеркнем, что точка (хо, yо) лежит на гиперболе.
Касательные к параболе
Если кривая задана уравнением
х = g(у),
то уравнение касательной к ней, проходящей через точку (хo,уo), где х0 = g (уо), можно записать в следующем виде
Пусть М0(х0, у0) — точка параболы. Пользуясь формулой (I), получаем уравнение касательной к параболе
Отсюда в силу равенства 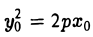
Замечание:
Сопоставляя канонические уравнения эллипса, гиперболы и параболы с уравнениями касательных к этим кривым, нетрудно заметить, что для получения последних не требуется специальных вычислений. В самом деле, заменяя у 2 на уу 0 , а х 2 на хх 0 (в случае параболы 2х нужно заменить на x + х 0 ). приходим к уравнению соответствующей касательной. Еще раз отметим, что сказанное справедливо лишь в том случае, когда точка (x 0 . y 0 ) лежит на кривой.
Оптическое свойство эллипса
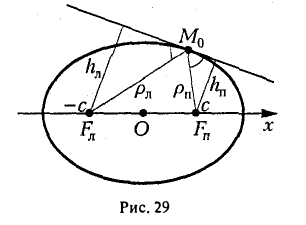
Пусть М 0 — произвольная точка эллипса
Как уже отмечалось, расстояния от нее до фокусов Fл и F n — фокальные радиусы — равны соответственно
Проведем через точку М 0 касательную к эллипсу,
и вычислим, на каком расстоянии от этой касательной лежат фокусы Fл (-c, 0) и Fn (c; 0) (напомним, что для этого следует воспользоваться формулой (10).
— нормирующий множитель (рис. 29). Нетрудно проверить, что
Обратившись к рис.29, заметим, что вычисленные отношения равны синусам углов, образованных касательной и фокальными радиусами точки касания. Из того, что синусы этих углов равны, вытекает равенство и самих углов. Тем самым доказано оптическое свойство эллипса: касательная к эллипсу образует равные углы с фокальными радиусами точки касания.
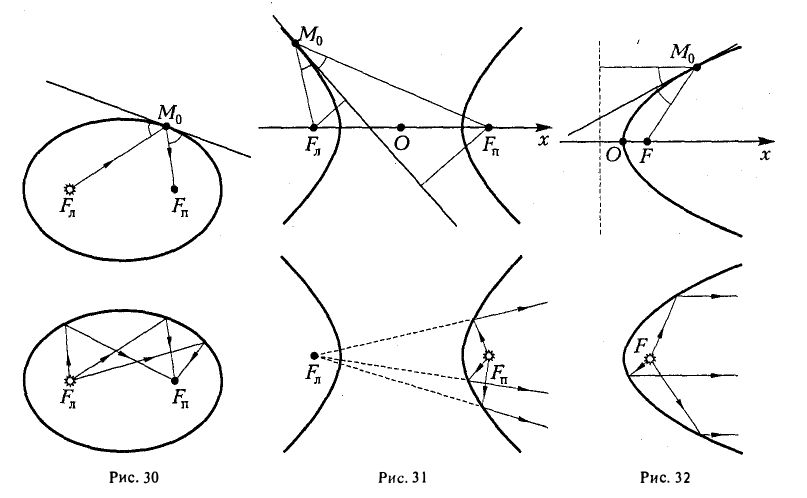
Это свойство называется оптическим по следующей причине: если поместить в один из фокусов эллипса с зеркальной «поверхностью» точечный источник света, то все лучи после отражения от «поверхности» эллипса сойдутся в другом его фокусе (рис. 30).
Оптическое свойство гиперболы
Устанавливается аналогичными выкладками и заключается в следующем.
Если поместить в один из фокусов гиперболы точечный источник света, то каждый луч после отражения от зеркальной «поверхности» гиперболы видится исходящим из другого фокуса (рис. 31).
Оптическое свойство параболы
Если в фокус параболы помещен точечный источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси параболы (рис. 32).
Классификация кривых второго порядка
Многочлены второй степени на плоскости
Теорема:
Пусть на плоскости введена прямоугольная декартова система координат Оху и пусть
— многочлен второй степени от переменных х и у.
Тогда на плоскости можно построить прямоугольную дека ртов у систему координат O’XY так, что после замены переменных х и у на переменные X и Y исходный многочлен f(x, у) приведется к многочлену F(X, Y) одного из следующих трех видов:
1-й шаг. Поворотом координатных осей на подходящим образом выбранный угол всегда можно добиться того, чтобы коэффициент при произведении разноименных координат обратился в нуль.
Пусть b ≠ 0 (при 6 = 0 этот шаг не нужен). Повернем оси координат вокруг точки О. Эта операция описывается следующими формулами
При этом координатные оси исходной системы Оху поворачиваются на угол φ (рис.33).
Заменим переменные х и у в формуле (1) их выражениями (2) через x’ и у’ и вычислим коэффициент 2b’ при произведении х’у’. Он равен
и обращается в нуль, если
Так как полученное уравнение разрешимо относительно φ, то указанным преобразованием всегда можно добиться обращения в нуль нужного коэффициента.
Приступая ко второму этапу преобразования, будем считать, что исходный многочлен f(x,у) уже имеет вид
где а 2 + с 2 >0. Для определенности положим с ≠ 0 (это не ограничивает общности наших рассуждений, так как заменой х, у в случае необходимости этого всегда можно добиться).
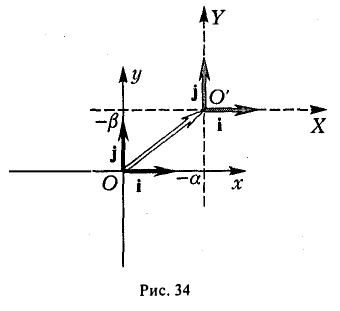
2-й шаг. Переносом начала координат можно достичь дальнейшего упрощения вида многочлена f(x,y). Эта операция описывается следующими формулами:
координатные оси новой системы O’XY получаются из координатных осей исходной системы Оху параллельным переносом в точку (-а, — β) (рис. 34).
Укажем конкретные значения а и β. Возможны три случая
I. а ≠ 0, с ≠ 0. Тогда, полагая
где А = а, В = с, С = g —
II. а = 0, d ≠ 0. Тогда, полагая
III. а = d = 0. Тогда, полагая
где В = с, Е = g —
Канонические уравнения кривых второго порядка
Если многочлен второй степени F(X, У) приравнять к нулю, то получим уравнение линии второго порядка
F(X, У) = 0.
Рассмотрим каждый из трех полученных выше случаев I, II, III отдельно.
I.
Э. А • В > 0. Домножением обеих частей уравнения на — 1 и заменой X на У, а У на X (в случае необходимости) всегда можно добиться того, чтобы В ≥ А > 0.
- С
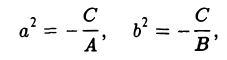
(мнимый эллипс)2). На действительной плоскости нет ни одной точки (X, Y), координаты которой обращали бы это уравнение в тождество.
Точка (0, 0) является единственной точкой плоскости, координаты которой удовлетворяют этому уравнению; точку (0,0) можно мыслить как действительную точку пересечения двух мнимых пересекающихся прямых 3).
Г. А • В 0, В
— пару пересекающихся прямых:
2) Название можно объяснить некоторым сходством этого уравнения с уравнением эллипса.
3) Название можно объяснить некоторым сходством этого уравнения с уравнением пары пересекающихся
прямых.
II. BY 2 + 2DX = О, В • D ≠ 0.
Всегда можно добиться того, чтобы В • D
III. BY 2 + Е = 0, В ≠ 0. Можно считать, что В > 0.
1. Е
Y 2 — с 2 = 0, с > 0
— пару параллельных прямых.
Y 2 — с 2 = 0, с 2 = 0
— пара совпадающих прямых.
Чтобы определить тип кривой второго порядка, не обязательно проводить все указанные выше преобразования. Достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.
— уравнение линии второго порядка. Введем следующие обозначения
Числа D и ∆ не зависят от выбора системы координат на плоскости и называются инвариантами. Из приводимой таблицы видно, какому сочетанию знаков определителей D и ∆ соответствует та или иная линия второго порядка.
Задача:
Убедитесь в том, что D и ∆ при рассмотренных преобразованиях системы координат действительно остаются неизменными.
4) Название можно объяснить некоторым сходством этого уравнения с уравнением пары параллельных прямых.
Поверхности второго порядка
Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Множество точек пространства, координаты х, у и z которых удовлетворяют равенству
F(x, у, z) = О,
называется поверхностью; равенство (*) называется уравнением этой поверхности.
Пример:
— уравнение сферы радиуса о с центром в точке (0,0,0) (рис. 35).
Рассмотрим многочлен второй степени от трех переменных х, у и z
Уравнение
F(x, y, z) = 0
будем называть уравнением поверхности второго порядка.
Исследование общего уравнения поверхностей второго порядка оказывается зна-чительноболее сложным, чем исследование общего уравнения кривых второго порядка, требует разработки соответствующего математического аппарата и будет проведено в конце главы VI.
В оставшихся параграфах этой главы мы сначала остановимся на изучении геометрических свойств некоторых важных классов общих поверхностей; затем используем их для рассмотрения канонических уравнений основных поверхностей второго порядка и исследования структуры этих поверхностей.
Некоторые классы поверхностей
Поверхности вращения
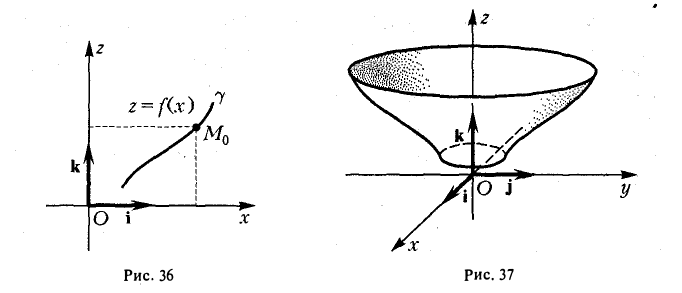
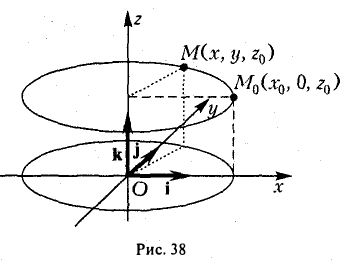
Рассмотрим на плоскости Oxz кривую γ, заданную уравнением
г = f(x), х ≥ 0
(рис. 36). При вращении кривой γ вокруг оси Oz она будет заметать некоторую поверхность, называемую поверхностью вращения (рис. 37). Найдем уравнение этой поверхности, т. е. равенство, которому должны удовлетворять координаты точек построенной поверхности и только они.
Тем самым, координаты х, у и z0 любой точки М этой окружности связаны следующим равенством
В силу произвольности выбора точки М0 на кривой γ искомое уравнение полученной поверхности вращения имеет вид
Цилиндрические поверхности
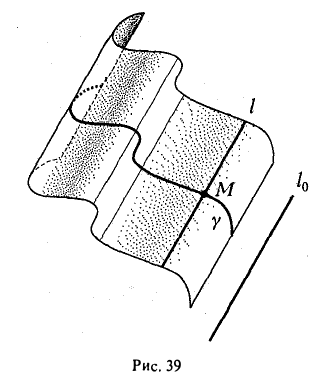
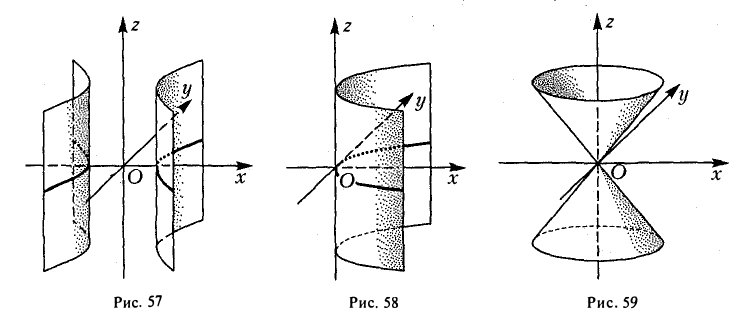
Через каждую точку некоторой заданной кривой γ проведем прямую l параллельно заданной прямой l0. Множество точек, лежащих на так построенных прямых, назовем цилиндрической поверхностью (рис. 39); кривая γ называется направляющей цилиндрической поверхности, а прямая l — ее образующей.
Найдем уравнение, описывающее цилиндрическую поверхность.
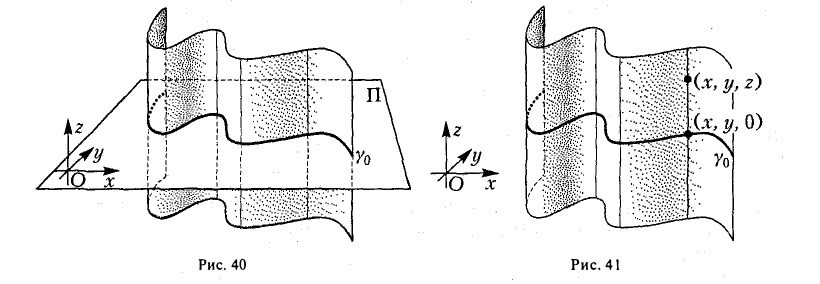
Возьмем произвольную точку О и проведем через нее плоскость П, перпендикулярную образующей I. Построим в пространстве прямоугольную координатную систему Oxyz, взяв за ось Oz прямую, перпендикулярную плоскости П. Тогда плоскость П будет координатной плоскостью Оху (рис.40). Плоскость П пересекает цилиндрическую поверхность по направляющей γ0.
F(x,y) = 0
— уравнение этой направляющей. Убедимся в том, что последнее соотношение можно считать уравнением искомой цилиндрической поверхности.
самом деле, пусть (х, у, z) — точка цилиндрической поверхности (рис. 41). Тогда точка (х, у, 0) лежит на γ0 и, значит, удовлетворяет уравнению
F(x,y)=0.
Но координаты точки (х, у, z) также обращают это уравнение в тождество. Последнее обстоятельство и позволяет считать соотношение F(x,y) = 0 искомым уравнением.
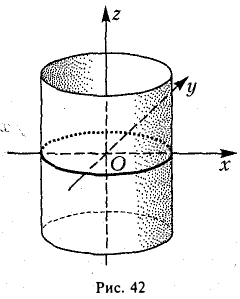
Пример:
Введем в пространстве прямоугольные декартовы координаты Охуz. Соотношение
является уравнением цилиндрической поверхности (эллиптического цилиндра) (рис. 42).
Замечание:
F(y, z) = 0
описывает цилиндрическую поверхность с образующей, параллельной координатной оси Оx, а уравнение
F(x,z) = 0
— цилиндрическую поверхность с образующей, параллельной оси Oy.
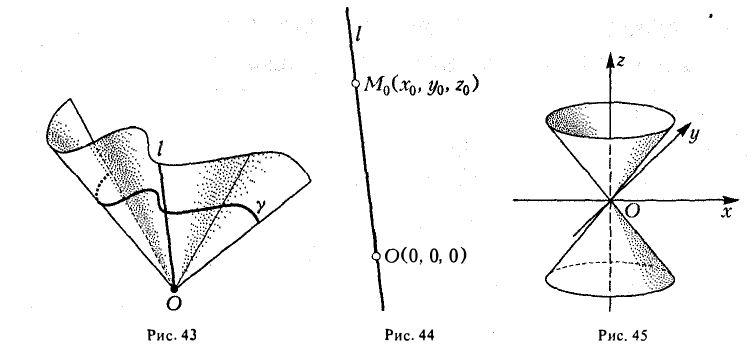
Конические поверхности
Пусть γ — произвольная кривая и О — точка вне eе. Через каждую точку кривой γ и точку О проведем прямую l. Множество точек, лежащих на построенных таким образом прямых, называется конической поверхностью (рис.43); кривая γ — направляющая конической поверхности, l — ее образующая, точка О — вершина. Рассмотрим функцию
F (x, у, z)
переменных х, у и z. Функция F(x, у, z) называется однородной функцией степени q, если для любого t > 0 выполняется равенство
Покажем, что если F(x, у, z) однородная функция, то F
является уравнением конической поверхности.
В самом деле, пусть
т.е. точка М0(xo, уо, zо) лежит на этой поверхности. Будем считать, что 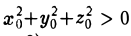
Подставляя полученные выражения для х, у и z в функцию F(x, у, z), видим, что
Это означает, что вся прямая l лежит на поверхности, определяемой уравнением F(x,y,z) = 0, которое, следовательно, и описывает коническую поверхность.
Пример:
является однородной функцией второй степени:
— уравнение конической поверхности (конуса второго порядка) (рис.45).
Воспользуемся теперь полученными выше результатами для исследования геометрической формы поверхностей второго порядка.
Эллипсоид. Гиперболоиды. Параболоиды. Цилиндры и конус второго порядка
Эллипсоид
Эллипсоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид
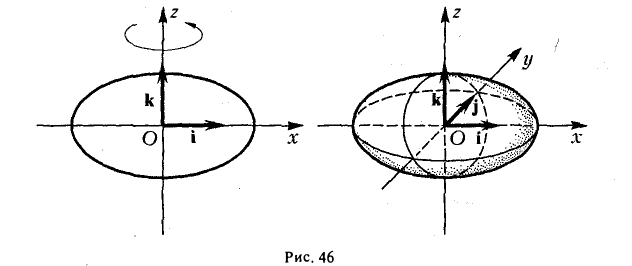
где а ≥ b ≥ с > 0. Для того, чтобы выяснить, как выглядит эллипсоид, поступим следующим образом. Возьмем на плоскости Oxz эллипс
и будем вращать его вокруг оси Oz (рис. 46).
— эллипсоид вращения — уже дает представление о том, как устроен эллипсоид общего вида. Чтобы получить его уравнение, достаточно равномерно сжать эллипсоид вращения . вдоль оси Оу с коэффициентом — 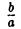
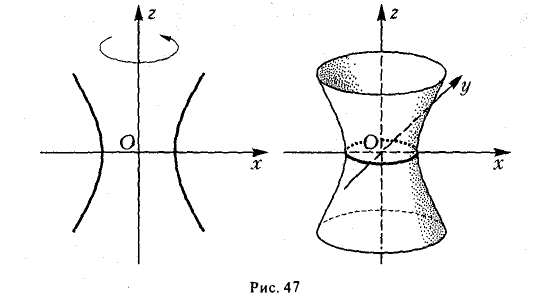
Гиперболоиды
вокруг оси Oz (рис. 47), получим поверхность, называемую однополостным гиперболоидом вращения. Его уравнение имеет вид
получается тем же способом, что и в случае эллипсоида вращения.
5) Эллипсоид вращения («) можно получить равномерным сжатием сферы х 2 + у 2 + z 2 = а 2 вдоль оси Оz с коэффициентом — 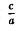
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом 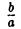
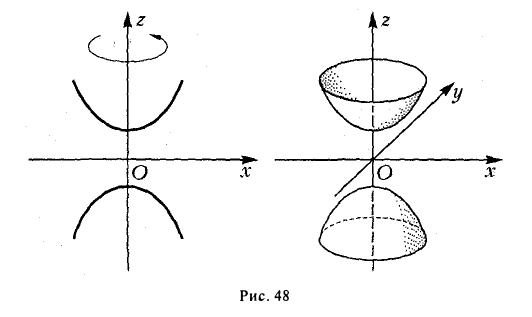
получается тем же способом, что и в разобранном выше случае эллипсоида. Путем вращения вокруг оси Oz сопряженной гиперболы
получим двуполостный гиперболоид вращения (рис.48). Его уравнение
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом 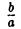
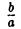
Эллиптический параболоид
вокруг оси Oz (рис.49), получаем параболоид вращения. Его уравнение имеет вид
Путем сжатия параболоида вращения вдоль оси Оу с коэффициентом 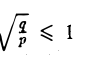
получается из уравнения параболоида вращения
путем замены у на 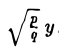
Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид
где р > 0, q > 0. Вид этой поверхности определим, применив так называемый метод сечений, который заключается в следующем: параллельно координатным плоскостям проводятся плоскости, пересекающие исследуемую поверхность, и по изменению конфигурации возникающих в результате плоских кривых делается вывод о структуре самой поверхности.
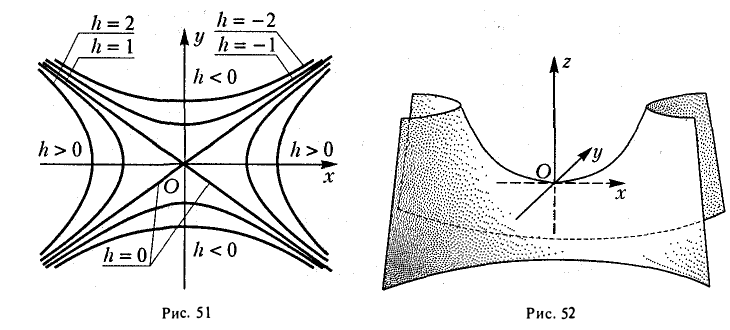
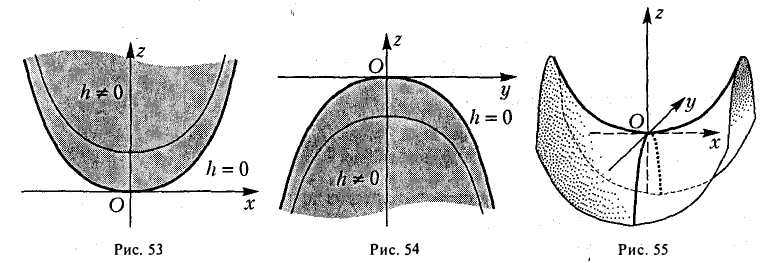
Начнем с сечений плоскостями z = h = const, параллельными координатной плоскости Оху. При h > 0 получаем гиперболы
при h
при h = 0 — пару пересекающихся прямых
Заметим, что эти прямые являются асимптотами для всех гипербол (т. е. при любом h ≠ 0). Спроектируем получаемые кривые на плоскость Ох у. Получим следующую картину (рис. 51). Уже это рассмотрение позволяет сделать заключение о седлообразном строении рассматриваемой поверхности (рис. 52).
Рассмотрим теперь сечения плоскостями
у = h.
Заменяя в уравнении поверхности у на h, получаем уравнения парабол (рис.53).
Аналогичная картина возникает при рассечении заданной поверхности плоскостями
х = h.
В этом случае также получаются параболы
ветви которых направлены вниз (а не вверх, как для сечения плоскостями у = h) (рис. 54).
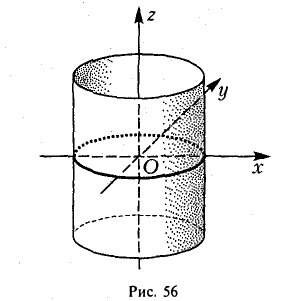
Используя последние два типа сечений, приходим к заключению, что гиперболический параболоид можно получить путем параллельного переноса параболы х2 = 2pz вдоль параболы у2 = -2qz, или наоборот (рис. 55).
Замечание:
Методом сeчeний можно разобраться в строении и всех ранее рассмотренных поверхностей второго порядка. Однако путем вращения кривых второго порядка и последующего равномерного сжатия к пониманию их структуры можно прийти проще и значительно быстрее.
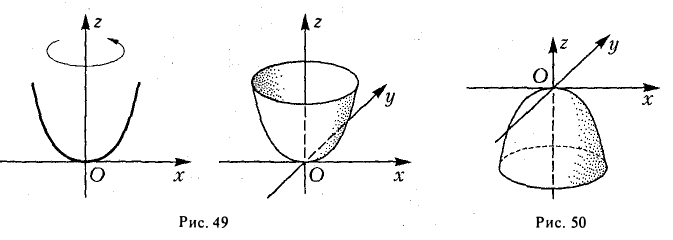
Оставшиеся поверхности второго порядка по существу уже рассмотрены ранее. Это цилиндры:
представление о котором можно получить либо путем вращения пары пересекающихся прямых
вокруг оси Oz и последующего сжатия, либо методом сечений. Конечно, в обоих случаях получим, что исследуемая поверхность имеет вид, указанный на рис. 59.
Дополнение к поверхностям второго порядка



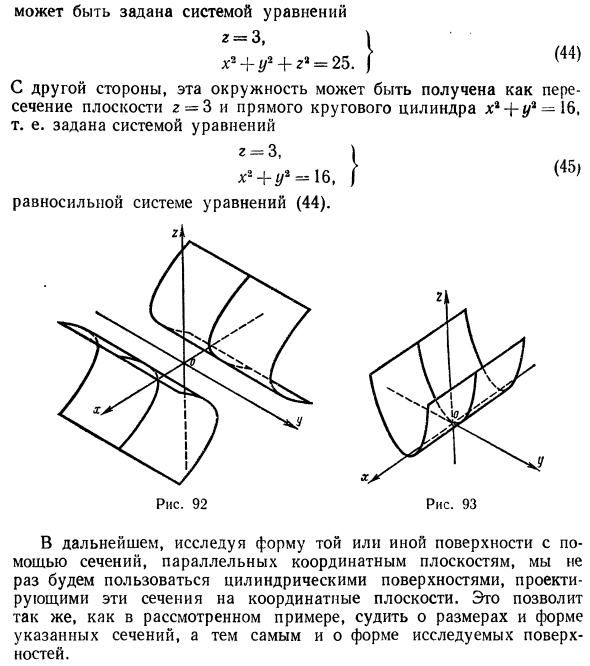


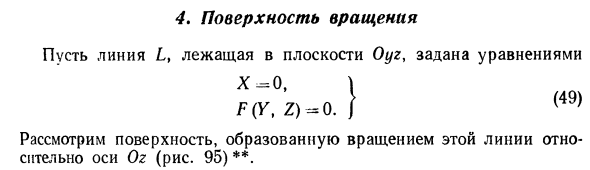




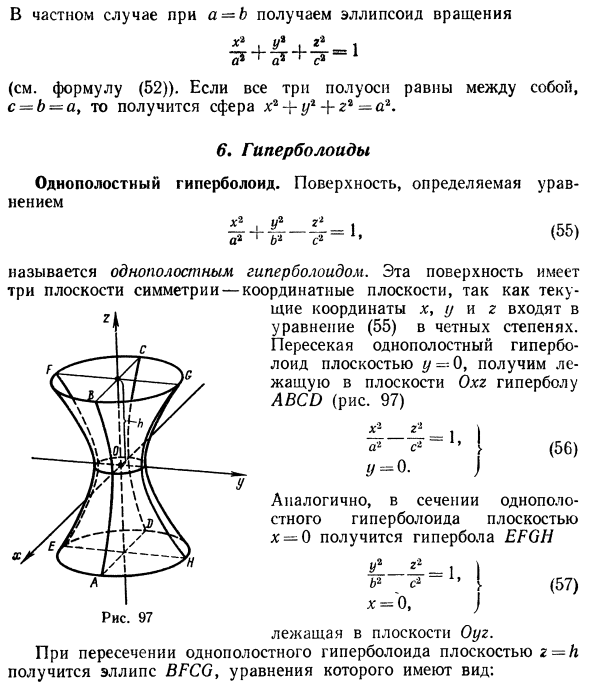
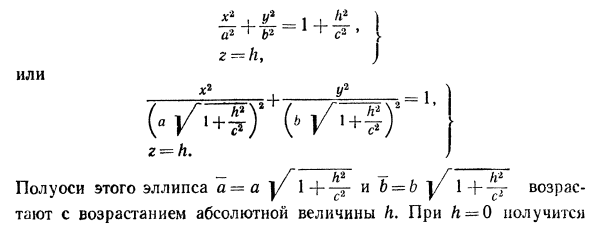

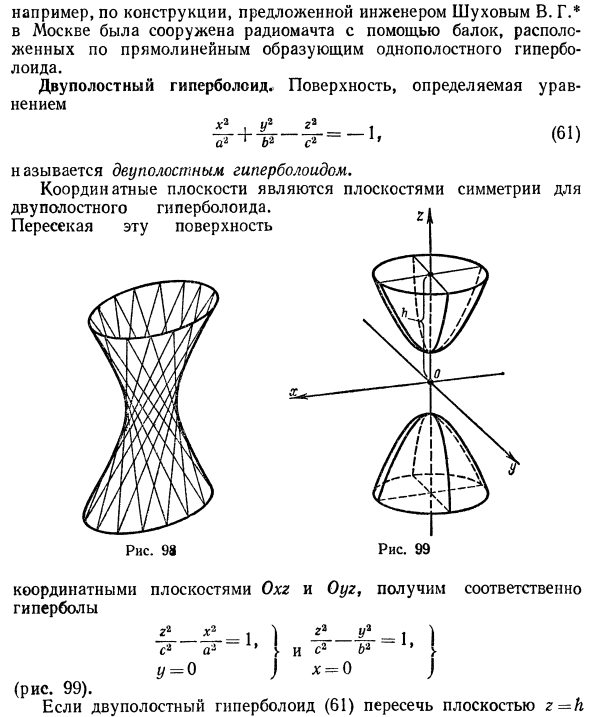
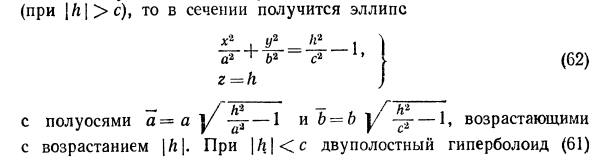

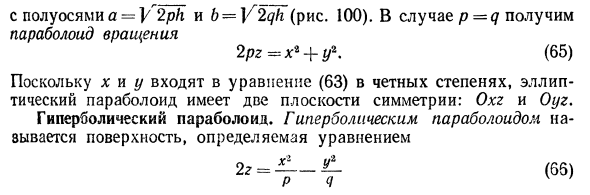
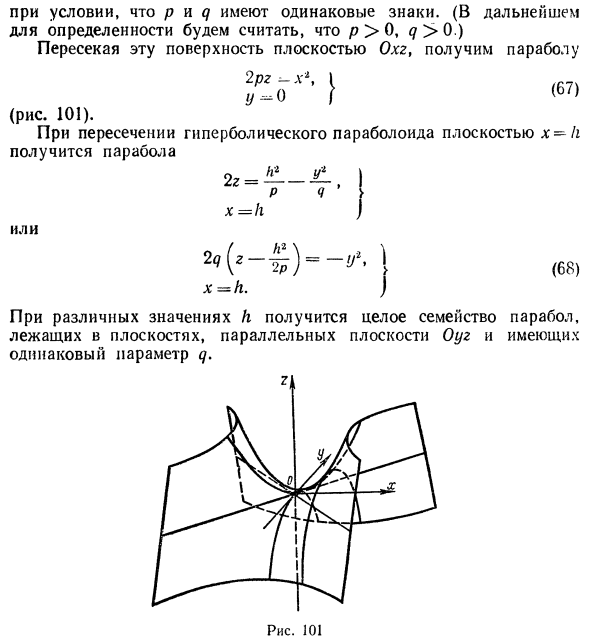

Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://univerlib.com/analytic_geometry/second_order_lines_and_surfaces/second_order_line/
http://lfirmal.com/poverhnosti-vtorogo-poryadka/