Общее уравнение в пространстве имеет вид

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x₀, y₀, z₀. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y₀, z₀. Тогда

.

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Вычитая из уравнения (1) тождество (2), получим

которая эквивалентна уравнению (1).

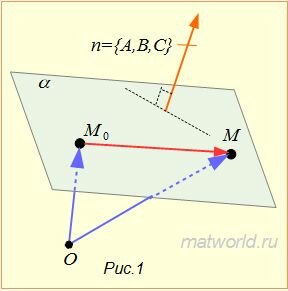Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n=<A,B,C> (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n=<A,B,C> и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

.

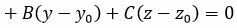Если же точка M(x, y, z) не лежит на плоскости α, то векторы n=<A,B,C> и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Вектор n=(A,B,C) называется нормальным вектором плоскости , определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным , если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным .

Рассмотрим все возможные варианты неполных уравнений плоскости:

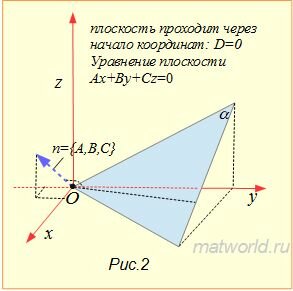
При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n=<0,B,C> лежит на координатной плоскости Oyz.

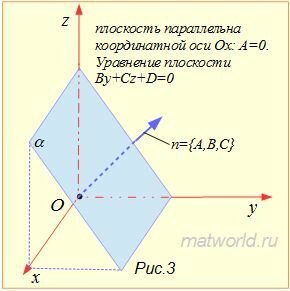При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

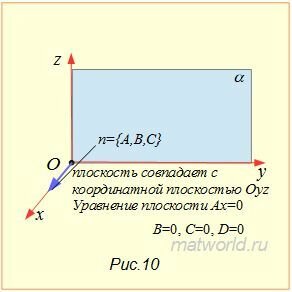
При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n=<A,B,C>=<0,0,1>, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n==<2,3,1>.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

Так как плоскость имеет нормальный вектор n=<A,B,C>=<2,3,1>, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Уравнения прямой, виды уравнений прямой в пространстве

Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.

Уравнение прямой в пространстве: общие сведения

Уравнение прямой на плоскости в прямоугольной системе координат O x y – это линейное уравнение с переменными x и y , которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек.

Если речь идет о прямой в трехмерном пространстве, все несколько иначе: не существует такого линейного уравнения с тремя переменными x , y , z , которому бы отвечали только координаты точек заданной прямой. В самом деле, уравнение A x + B y + C z + D = 0 , где x , y , z – переменные, а А , В , С и D – некоторые действительные числа ( А , В , С одновременно не равны нулю) – это общее уравнение плоскости. Тогда как же задать прямую линию в прямоугольной системе координат O x y z ? Найдем ответ на этот вопрос в следующих пунктах темы.

Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей

Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.

Рассмотрим это утверждение в алгебраическом толковании.

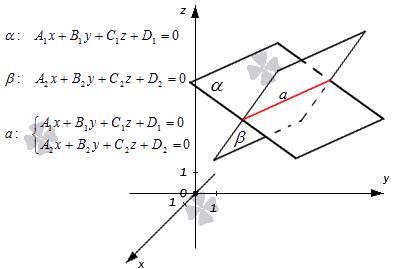
Допустим, в трехмерном пространстве зафиксирована прямоугольная система координат O x y z и задано, что прямая a – это линия пересечения двух плоскостей α и β , которые соответственно описываются уравнениями плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Поскольку прямая a – это множество общих точек плоскостей α и β , то координаты любой точки прямой a будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут.

Таким образом, координаты любой точки прямой a в прямоугольной системе координат станут частным решением системы линейных уравнений вида

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Общее же решение системы уравнений _ A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определит координаты каждой точки прямой a , т.е. по сути задает саму прямую a .

Резюмируем: прямая в пространстве в прямоугольной системе координат O x y z может быть задана системой уравнений двух плоскостей, которые пересекаются:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Приведем пример описания прямой линии в пространстве при помощи системы уравнений:

x + 3 y — 2 1 z + 11 3 y + 1 4 z — 2 = 0

Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.

Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.

Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.

Параметрические уравнения прямой в пространстве

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где x 1 , y 1 , z 1 – координаты некой точки прямой; а x , а y и a z (одновременно не равны нулю) – координаты направляющего вектора прямой. а · λ – некий параметр, принимающий любые действительные значения.

Любое значение параметра λ позволяет, используя параметрические уравнения прямой в пространстве, определить тройку чисел ( x , y , z ) , соответствующую некой точке прямой (отсюда и название такого вида уравнений). Например, пусть λ = 0 , тогда из параметрических уравнений прямой в пространстве получим координаты:

x = x 1 + a x · 0 y = y 1 + a y · 0 z = z 1 + a z · 0 ⇔ x = x 1 y = y 1 z = z 1

Рассмотрим конкретный пример:

Пусть прямая задана параметрическими уравнениями вида x = 3 + 2 · a x y = — 2 · a y z = 2 + 2 · a z .

Заданная прямая проходит через точку М 1 ( 3 , 0 , 2 ) ; направляющий вектор этой прямой имеет координаты 2 , — 2 , 2 .

Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.

Канонические уравнения прямой в пространстве

Если разрешить каждое из параметрических уравнений прямой

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ относительно параметра λ , возможно просто перейти к каноническим уравнениям прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z .

Канонические уравнения прямой в пространстве задают прямую, которая проходит через точку М 1 ( x 1 , y 1 , z 1 ) , и у которой направляющий вектор равен a → = ( a x , a y , a z ) . Например, задана прямая, описываемая каноническим уравнением x — 1 1 = y 2 = z + 5 7 . Эта прямая проходит через точку с координатами ( 1 , 0 , — 5 ) , ее направляющий вектор имеет координаты ( 1 , 2 , — 7 ) .

Отметим, что одно или два числа из чисел а x , а y и а z в канонических уравнениях прямой могут быть равны нулю (все три числа не могут быть равны нулю, поскольку направляющий вектор не может быть нулевым). В таком случае запись вида x — x 1 a x = y — y 1 a y = z — z 1 a z является формальной (поскольку в знаменателях одной или двух дробей будут нули) и понимать ее нужно как:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где λ ∈ R .

Если одно из чисел а x , а y и a z канонического уравнения прямой равно нулю, то прямая лежит в какой-то из координатных плоскостей, или в плоскости, ей параллельной. Если два из чисел а x , а y и a z равны нулю, то прямая или совпадает с какой-либо из координатных осей, или параллельна ей. К примеру, прямая, описываемая каноническим уравнением x + 4 3 = y — 5 2 = z + 2 0 , лежит в плоскости z = — 2 , параллельной координатной плоскости O x y , а координатная ось O y описывается каноническими уравнениями x 0 = y 1 = z 0 .

Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.

Уравнения прямой, виды уравнений прямой в пространстве.

Эта статья является продолжением темы прямая в пространстве. Здесь мы от геометрического описания прямой линии в пространстве перейдем к алгебраическому описанию, то есть, определим прямую с помощью уравнений в фиксированной прямоугольной системе координат Oxyz в трехмерном пространстве.

Статья построена следующим образом: сначала приведена общая информация, которая раскрывает значение фразы «уравнения прямой в пространстве», после этого рассмотрены уравнения прямой в пространстве различного вида, показана связь между ними и приведены примеры уравнений прямой.

Навигация по странице.

Уравнения прямой в пространстве – начальные сведения.

Уравнение прямой на плоскости в прямоугольной системе координат Oxy представляет собой линейное уравнение с двумя переменными x и y , которому удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точек. С прямой в трехмерном пространстве дело обстоит немного иначе – не существует линейного уравнения с тремя переменными x , y и z , которому бы удовлетворяли только координаты точек прямой, заданной в прямоугольной системе координат Oxyz . Действительно, уравнение вида , где x , y и z – переменные, а A , B , C и D – некоторые действительные числа, причем А , В и С одновременно не равны нулю, представляет собой общее уравнение плоскости. Тогда встает вопрос: «Каким же образом можно описать прямую линию в прямоугольной системе координат Oxyz »?

Ответ на него содержится в следующих пунктах статьи.

Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей.

Напомним одну аксиому: если две плоскости в пространстве имеют общую точку, то они имеют общую прямую, на которой находятся все общие точки этих плоскостей. Таким образом, прямую линию в пространстве можно задать, указав две плоскости, пересекающиеся по этой прямой.

Переведем последнее утверждение на язык алгебры.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и известно, что прямая a является линией пересечения двух плоскостей и , которым отвечают общие уравнения плоскости вида и соответственно. Так как прямая a представляет собой множество всех общих точек плоскостей и , то координаты любой точки прямой a будут удовлетворять одновременно и уравнению и уравнению , координаты никаких других точек не будут удовлетворять одновременно обоим уравнениям плоскостей. Следовательно, координаты любой точки прямой a в прямоугольной системе координат Oxyz представляют собой частное решение системы линейных уравнений вида , а общее решение системы уравнений определяет координаты каждой точки прямой a , то есть, определяет прямую a .

Итак, прямая в пространстве в прямоугольной системе координат Oxyz может быть задана системой из уравнений двух пересекающихся плоскостей .

Вот пример задания прямой линии в пространстве с помощью системы двух уравнений — .

Рекомендуем продолжить изучение этой темы, обратившись к статье уравнения прямой в пространстве — уравнения двух пересекающихся плоскостей. В ней дана более детальная информация, подробно разобраны решения характерных примеров и задач, а также показан способ перехода к уравнениям прямой в пространстве другого вида.

Следует отметить, что существуют различные способы задания прямой в пространстве, и на практике прямая чаще задается не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, лежащей на этой прямой. В этих случаях проще получить канонические и параметрические уравнения прямой в пространстве. О них поговорим в следующих пунктах.

Параметрические уравнения прямой в пространстве.

Параметрические уравнения прямой в пространстве имеют вид , где x₁ , y₁ и z₁ – координаты некоторой точки прямой, a_x , a_y и a_z ( a_x , a_y и a_z одновременно не равны нулю) — соответствующие координаты направляющего вектора прямой, а — некоторый параметр, который может принимать любые действительные значения.

При любом значении параметра по параметрическим уравнениям прямой в пространстве мы можем вычислить тройку чисел , она будет соответствовать некоторой точке прямой (отсюда и название этого вида уравнений прямой). К примеру, при из параметрических уравнений прямой в пространстве получаем координаты x₁ , y₁ и z₁ : .

В качестве примера рассмотрим прямую, которую задают параметрические уравнения вида . Эта прямая проходит через точку , а направляющий вектор этой прямой имеет координаты .

Рекомендуем продолжить изучение темы, обратившись к материалу статьи параметрические уравнения прямой в пространстве. В ней показан вывод параметрических уравнений прямой в пространстве, разобраны частные случаи параметрических уравнений прямой в пространстве, даны графические иллюстрации, приведены развернутые решения характерных задач и указана связь параметрических уравнений прямой с другими видами уравнений прямой.

Канонические уравнения прямой в пространстве.

Разрешив каждое из параметрических уравнений прямой вида относительно параметра , легко перейти к каноническим уравнениям прямой в пространстве вида .

Канонические уравнения прямой в пространстве определяют прямую, проходящую через точку , а направляющим вектором прямой является вектор . К примеру, уравнения прямой в каноническом виде соответствуют прямой, проходящей через точку пространства с координатами , направляющий вектор этой прямой имеет координаты .

Следует отметить, что одно или два из чисел в канонических уравнениях прямой могут быть равны нулю (все три числа одновременно не могут быть равны нулю, так как направляющий вектор прямой не может быть нулевым). Тогда запись вида считается формальной (так как в знаменателях одной или двух дробей будут нули) и ее следует понимать как , где .

Если одно из чисел в канонических уравнениях прямой равно нулю, то прямая лежит в одной из координатных плоскостей, либо в плоскости ей параллельной. Если два из чисел равны нулю, то прямая либо совпадает с одной из координатных осей, либо параллельна ей. Например прямая, соответствующая каноническим уравнениям прямой в пространстве вида , лежит в плоскости z=-2 , которая параллельна координатной плоскости Oxy , а координатная ось Oy определяется каноническими уравнениями .

Графические иллюстрации этих случаев, вывод канонических уравнений прямой в пространстве, подробные решения характерных примеров и задач, а также переход от канонических уравнений прямой к другим уравнениям прямой в пространстве смотрите в статье канонические уравнения прямой в пространстве.