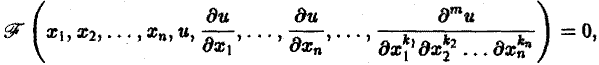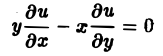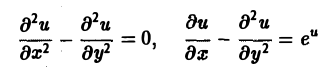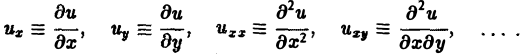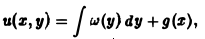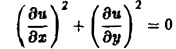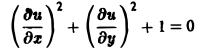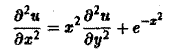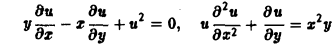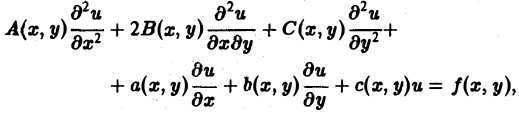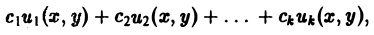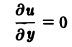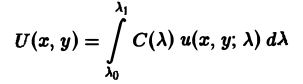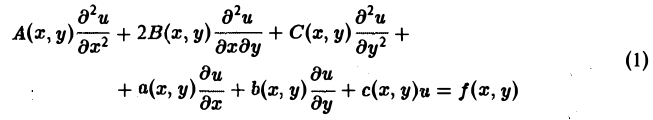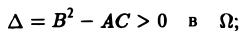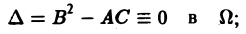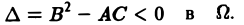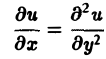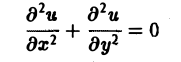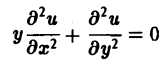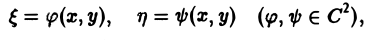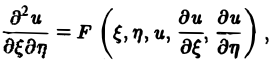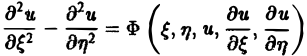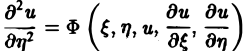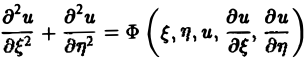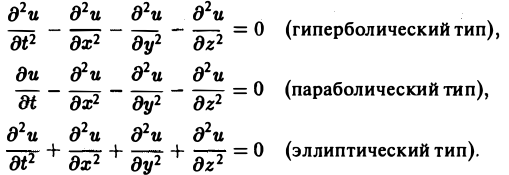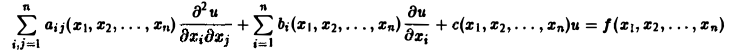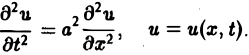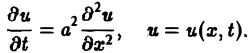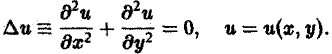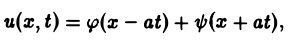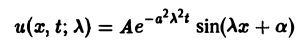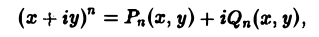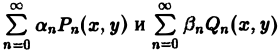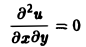Общее уравнение второго порядка с тремя переменными

Дифференциальные уравнения в частных производных с примерами решения и образцами выполнения

Дифференциальным уравнением с частными производными называется уравнение вида
(1)

связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т.

Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то

— дифференциальное уравнение 1-го порядка;

— дифференциальные уравнения 2-го порядка.

Для упрощения записи пользуются также следующими обозначениями:

Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через С m (D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно.

Определение:

Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ С m (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D.

Пример:

Найти решение и = и(х,у) уравнения

Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у,

u = φ(y). (3)

Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2).

Приме:

Найти решение u = u(z, у) уравнения

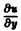
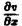
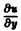
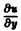
Положим = о. Тогда уравнение (4) примет вид = 0. Его общим решением будет произвольная функция v = w(у). Поскольку v= приходим к уравнению = w(у). Интегрируя по у (считая х параметром), получим

где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде

u(x, y) = f(y) + g(x) (5)

произвольные дифференцируемые функции).

Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g.

Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты.

Пример:

Множество действительных решений уравнения

исчерпывается функцией u(x, y) = const, а уравнение

вовсе не имеет действительных решений.

Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.

Линейные дифференциальные уравнения с частными производными. Свойства их решений

Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.

Пример:

— линейное уравнение; уравнения

Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид
(1)

где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным.

Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде

L[u] = f(x, у). (2)

Соответствующее однородное уравнение запишется так:

L[u] = 0. (3)

Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C 2 (D) функций и = и(х, у).

Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.

Теорема:

Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3).

Теорема:

Если и₁(х, у) и и₂(х, у) — решения линейного однородного уравнения (3), то сумма и₁(х, у) + и₂(x, у) есть также решение этого уравнения.

Следствие:

Если каждая из функций и₁(х, у) и и₂(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация

где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения.

В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная

комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.

Пример:

имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, х n ,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами 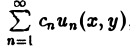, членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.

Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла

по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения

L[u] = f (4)

справедливы следующие предложения.

Теорема:

Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4).

Теорема:

Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2.

Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными

Определение:

Линейное дифференциальное уравнение второго порядка

в некоторой области Q на плоскости хОу называется

1) гиперболическим в Ω, если

2) параболическим в Ω, если

3) эллиптическим в Ω, если

Пользуясь этим определением, легко проверить, что уравнения

— гиперболические при всех х и у, уравнение

— параболическое при всех х и у, а уравнение

— эллиптическое при всех х и у. Уравнение

— эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у

с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.

Уравнение гиперболического типа (∆ > 0) преобразуется к вшу

(два канонических вида уравнений гиперболического типа).

Уравнение параболического типа (∆ ≡ 0) преобразуется к виду

(канонический вид уравнения параболического типа).

Уравнение эллиптического типа (∆

(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных 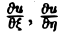и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).

В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.

Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo).

Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид

Здесь и = и(х, у, z, t).

Замечание:

В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами

к каноническому виду возможно только в данной точке 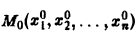и невозможно в любой сколь угодно малой окрестности этой точки.

Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач.

Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2)

Здесь х — пространственная координата, t — время, 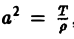где Т — натяжение струны, р — ее линейная плотность.

Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
(3)

Здесь 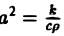где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.

Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
(4)

Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида

Можно показать, что решениями уравнения (3) являются функции вида

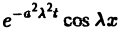
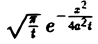
произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) = уравнения теплопроводности.

Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения

являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции

f(z) = u(x, у) + iv(x, у)

комплексного переменного z = х + iy являются решениями уравнения Лапласа (4).

В силу линейности уравнения (4) ряды

тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у.

Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.

Постановка основных задач для линейных дифференциальных уравнений второго порядка

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений.

Пример:

Общее решение уравнения

имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.

Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п):

а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством R n , граничные условия отсутствуют;

б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют;

в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ R n

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Система линейных уравнений с тремя переменными

Линейное уравнение с тремя переменными и его решение

Уравнение вида ax+by+cz = d , где a, b, c, d — данные числа, называется линейным уравнением с тремя переменными x, y и z.

Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; \frac<1> <2>x-8y-5z = 7$

Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.

Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$

Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.

О тождествах – см. §3 данного справочника

Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.

Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве .

Решение системы линейных уравнений с тремя переменными методом подстановки

Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)

Например: решить систему

$$ <\left\< \begin 3x+2y-z = 8 \\ x-y+z = -2 \\ 2x-3y-5z = 1 \end \right.> \Rightarrow <\left\< \begin 3(y-z-2)+2y-z = 8 \\ x = y-z-2 \\ 2(y-z-2)-3y-5z = 1 \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin x = y-z-2 \\ 5y-4z = 14 \\ -y-7z = 5 \end \right.> \Rightarrow <\left\< \begin x = y-z-2 \\ y = -7z-5 \\ 5(-7z-5)-4z = 14 \end \right.> \Rightarrow <\left\< \begin x = y-z-2 \\ y = -7z-5 \\ -39z = 39 \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin x = 2-(-1)-2 = 1 \\ y = -7\cdot(-1)-5 = 2 \\ z = -1 \end \right.> \Rightarrow <\left\< \begin x = 1 \\ y = 2 \\ z = -1 \end \right.> $$

Решение системы линейных уравнений с тремя переменными методом Крамера

Для системы с 3-мя переменными действуем по аналогии.

Дана система 3-х линейных уравнений с 3-мя переменными:

$$ <\left\< \begin a_1 x+b_1 y+c_1 z = d_1 \\ a_2 x+b_2 y+c_2 z = d_2 \\ a_3 x+b_3 y+c_3 z = d_3 \end \right.> $$

Определим главный определитель системы:

$$ \Delta = \begin a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end $$

и вспомогательные определители :

$$ \Delta_x = \begin d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \\ d_3 & b_3 & c_3 \end, \Delta_y = \begin a_1 & d_1 & c_1 \\ a_2 & d_2 & c_2 \\ a_3 & d_3 & c_3 \end, \Delta_z = \begin a_1 & b_1 & d_1 \\ a_2 & b_2 & d_2 \\ a_3 & b_3 & d_3 \end $$

Тогда решение системы:

Соотношение значений определителей, расположения плоскостей и количества решений:

Три плоскости пересекаются в одной точке

Три плоскости параллельны

Две или три плоскости совпадают или пересекаются по прямой

Бесконечное множество решений

Осталось определить правило вычисления определителя 3-го порядка.

Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):

$$ \Delta = \begin a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end = a_1 = \begin b_2 & c_2 \\ b_3 & c_3 \end — b_1 = \begin a_2 & c_2 \\ a_3 & c_3 \end + c_1 = \begin a_2 & b_2 \\ a_3 & b_3 \end = $$

$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$

Примеры

Пример 1. Найдите решение системы уравнений методом подстановки:

$$<\left\< \begin z = 3x+2y-13 \\ 2x-y+3(3x+2y-13) = -2 \\ x+2y-(3x+2y-13) = 9 \end \right.> \Rightarrow <\left\< \begin z = 3x+2y-13 \\ 11x+5y = 37 \\ -2x = -4 \end \right.> \Rightarrow $$

$$\Rightarrow <\left\< \begin z = 3\cdot2+2\cdot3-13 = -1 \\ y = \frac<37-11\cdot2> <5>= 3 \\ x = 2 \end \right.> \Rightarrow <\left\< \begin x = 2 \\ y = 3 \\ z = -1 \end \right.> $$

$$ <\left\< \begin x = -y-3z+6 \\ 2(-y-3z+6)-5y-z = 5\\ (-y-3z+6)+2y-5z = -11 \end \right.> \Rightarrow <\left\< \begin x = -y-3z+6 \\ -7y-7z = -7 |:(-7) \\ y-8z = -17 \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin x = -y-3z+6 \\ y+z = 1 \\ y-8z = -17 \end \right.> \Rightarrow <\left\< \begin x = -y-3z+6 \\ 9z = 18 \\ y = 1-z \end \right.> \Rightarrow <\left\< \begin x = 1-6+6 = 1 \\ z = 2 \\ y = 1-2 = -1 \end \right.> \Rightarrow$$

Пример 2. Найдите решение системы уравнений методом Крамера:

$$ \Delta = \begin 3 & 2 & -1 \\ 2 & -1 & 3\\ 1 & 2 & -1 \end = 3 = \begin -1 & 3 \\ 2 & -1 \\ \end — 2 = \begin 2 & 3 \\ 1 & -1 \\ \end — 1 = \begin 2 & -1 \\ 1 & 2 \\ \end = $$

$$ \Delta_x = \begin 13 & 2 & -1 \\ -2 & -1 & 3 \\ 9 & 2 & -1 \\ \end = 13 = \begin -1 & 3 \\ 2 & -1 \\ \end — 2 = \begin -2 & 3 \\ 9 & -1 \\ \end — 1 = \begin -2 & -1 \\ 9 & 2 \\ \end = $$

$$ \Delta_y = \begin 3 & 13 & -1 \\ 2 & -2 & 3 \\ 1 & 9 & -1 \\ \end = 3 = \begin -2 & 3 \\ 9 & -1 \\ \end — 13 = \begin 2 & 3 \\ 1 & -1 \\ \end — 1 = \begin 2 & -2 \\ 1 & 9 \\ \end = $$

$$ \Delta_z = \begin 3 & 2 & 13 \\ 2 & -1 & -2 \\ 1 & 2 & 9 \\ \end = 3 = \begin -1 & -2 \\ 2 & 9 \\ \end — 2 = \begin 2 & -2 \\ 1 & 9 \\ \end + 13 = \begin 2 & -1 \\ 1 & 2 \\ \end = $$

$$ \Delta = \begin 1 & 1 & 3 \\ 2 & -5 & -1\\ 1 & 2 & -5 \end = 1 = \begin -5 & -1 \\ 2 & -5 \\ \end — 1 = \begin 2 & -1 \\ 1 & -5 \\ \end + 3 = \begin 2 & -5 \\ 1 & 2 \\ \end = $$

$$ \Delta_x = \begin 6 & 1 & 3 \\ 5 & -5 & -1 \\ -11 & 2 & -5 \\ \end = 6 = \begin -5 & -1 \\ 2 & -5 \\ \end — 1 = \begin 5 & -1 \\ -11 & -5 \\ \end + 3 = \begin 5 & -5 \\ -11 & 2 \\ \end = $$

$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$

$$ \Delta_y = \begin 1 & 16 & 3 \\ 2 & 5 & -1 \\ 1 & -11 & -5 \\ \end = 1 = \begin 5 & -1 \\ -11 & -5 \\ \end — 6 = \begin 2 & -1 \\ 1 & -5 \\ \end + 3 = \begin 2 & 5 \\ 1 & -11 \\ \end = $$

$$ \Delta_z = \begin 1 & 1 & 6 \\ 2 & -5 & 5 \\ 1 & 2 & -11 \\ \end = 1 = \begin -5 & 5 \\ 2 & -11 \\ \end — 1 = \begin 2 & 5 \\ 1 & -11 \\ \end + 6 = \begin 2 & -5 \\ 1 & 2 \\ \end = $$

Пример 3*. Решите систему уравнений относительно x,y,и z:

$$ a \neq b, b \neq c, a \neq c $$

Решаем методом замены:

$$ <\left\< \begin z = -(a^3+a^2 x+ay)\\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \\ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 \end \right.> \Rightarrow <\left\< \beginz = -(a^3+a^2 x+ay)\\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \\ (c^2-a^2 )x+(c-a)y = a^3-c^3 \end \right.> $$

Т.к. $ a \neq b$ второе уравнение можно сократить на $(a-b) \neq 0$

Т.к.$ a \neq c$ третье уравнение можно сократить на $(a-с) \neq 0 $. В третьем уравнении после сокращения поменяем знаки:

Из второго уравнения получаем:

Т.к. $b \neq c$ можно сократить на $(b-c) \neq 0$:

$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$

$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$

ЛДУ с переменными коэффициентами. Метод Лагранжа

Линейные дифференциальные уравнения с переменные коэффициентами

Если известно частное решение уравнения

то его порядок можно понизить на единицу (не нарушая линейности уравнения), полагая , где — новая неизвестная функция, а затем делая замену (можно непосредственно делать замену ).

Если известно частных линейно независимых решений уравнения (32), то порядок уравнения может быть понижен на единиц.

Общее решение уравнения

есть сумма какого-нибудь его частного решения и общего решения соответствующего однородного уравнения (32).

Если известна фундаментальная система соответствующего однородного уравнения (32), то общее решение неоднородного уравнения (33) может быть найдено методом вариации постоянных ( метод Лагранжа ).

Общее решение уравнения (32) имеет вид

где — произвольные постоянные.

Будем искать решение уравнения (33) в виде

где — некоторые пока неизвестные функции от . Для их определения получаем систему

Разрешая эту систему относительно , получаем

где — произвольные постоянные. Внося найденные значения в (34), получаем общее решения уравнения (33).

В частности, для уравнения второго порядка

Решая (36) относительно и , получаем

где и — постоянные интегрирования.

Замечание. Для уравнения , где , система (36) будет выглядеть так:

Пример 1. Найти общее решение уравнения , если есть его частное решение.

Решение. Положим , где — новая неизвестная функция от , тогда

Подставляя в данное уравнение, получаем

Но так как есть частное решение данного уравнения, то , поэтому имеем

Но , а значит , и уравнение (37) примет вид

Перепишем его в виде . Отсюда имеем , откуда

Интегрируя это уравнение, найдем и, следовательно, общее решение данного уравнения будет

Пример 2. Найти общее решение уравнения .

Решение. Общее решение соответствующего однородного уравнения имеет вид (см. пример 1)

и следовательно, его фундаментальная система решений будет

Будем искать общее решение данного уравнения методом вариации произвольных постоянных:

где — постоянные неизвестные функции от , подлежащие определению. Для их нахождения составим следующую систему:

Отсюда находим: . Интегрируя, получаем

Подставляя эти значения и в выражение для , найдем общее решение данного уравнения

Пример 3. Решить уравнение .

Решение. Соответствующее однородное уравнение будет . Его характеристическое уравнение имеет мнимые корни , и общее решение однородного уравнения имеет вид

Общее решение исходного уравнения ищем в виде

где и — неизвестные функции от . Для их нахождения составим систему

Разрешаем эту систему относительно и :

Подставляя выражения и в (38), получаем общее решение данного уравнения

Здесь есть частное решение исходного неоднородного уравнения.

Пример 4. Зная фундаментальную систему решений соответствующего однородного уравнения, найти частное решение уравнения

Решение. Применяя метод вариации постоянных, находим общее решение уравнения (39):

При первые два слагаемых правой части (40) стремятся к бесконечности, причем при любых , неравных нулю одновременно, функция есть бесконечно большая функция при . Третье слагаемое правой части (40) имеет пределом ноль при , что легко установить с помощью правила Лопиталя. Таким образом, функция , которая получается из (40) при и , будет решением уравнения (39), удовлетворяющим условию .

Составление дифференциального уравнения по заданной фундаментальной системе решений

Рассмотрим линейно независимую на отрезке систему функций

имеющих все производные до n-го порядка включительно. Тогда уравнение

где — неизвестная функция, будет линейным дифференциальным уравнением, для которого, как нетрудно видеть, функции составляют фундаментальную систему решений. Коэффициент при в (42) есть определитель Вронского системы (41). Те точки, в которых этот определитель обращается в ноль, будут особыми точками построенного уравнения — в этих точках обращается в ноль коэффициент при старшей производной .

Пример 1. Составить дифференциальное уравнение, для которого образуют фундаментальную систему решений.

Решение. Применяя формулу (42), получаем

Раскрывая определитель в левой части (43) по элементам третьего столбца, будем иметь . Это и есть искомое дифференциальное уравнение.

Пример 2. Составить дифференциальное уравнение, для которого функции фундаментальную систему решений образуют функции .

Решение. Составим уравнение вида (42):

Раскрывая последний определитель по элементам 3-го столбца, будем иметь

В этом примере определитель Вронского обращается в ноль при . Это не противоречит общей теории, в силу которой определитель Вронского фундаментальной системы решений линейного однородного дифференциального уравнения

с непрерывными на отрезке коэффициентами не обращается в ноль ни в одной точке отрезка . Записав уравнение (44) в виде

видим, что коэффициент при терпит разрыв при , так что в точке непрерывность коэффициентов уравнения (45) нарушается.

Разные задачи

Пусть — фундаментальная система линейного однородного уравнения

Тогда имеет место формула Остроградского–Лиувилля

где — определитель Вронского, а — любое значение из отрезка , на котором непрерывны коэффициенты уравнения.

Пример 1. Показать, что линейное дифференциальное уравнение имеет решение вида , где — некоторый многочлен. Показать, что второе решение этого уравнения имеет вид , где — также многочлен.

Решение. Будем искать решение в виде многочлена, например, первой степени: . Подставляя в уравнение, найдем, что . Пусть , тогда ;. таким образом, многочлен будет решением данного уравнения. Перепишем данное уравнение в виде

Пусть — второе частное решение данного уравнения, линейно независимое с первым. Находим определитель Вронского системы решений

здесь . Применяя формулу Остроградского–Лиувилля, будем иметь

где — любое значение , причем , или ; здесь . Для нахождения получили линейное дифференциальное уравнение первого порядка. Деля обе части этого уравнения на , приведем его к виду