Общее уравнение второго порядка типы линий

ОБЩЕЕ УРАВНЕНИЕ ЛИНИЙ ВТОРОГО ПОРЯДКА

Линии второго порядка

1. Основные понятия.

6. Общее уравнение линий второго порядка.

ОСНОВНЫЕ ПОНЯТИЯ

Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

.

Коэффициенты уравнения – действительные числа, но, по крайней мере, одно из чисел отлично от нуля. Такие линии называются линиями (кривыми) второго порядка.

ОКРУЖНОСТЬ

Простейшей кривой второго порядка является окружность.

Определение. Окружностью радиуса R с центром в точке называется множество всех точек плоскости, удовлетворяющих условию .

Каноническое уравнение окружности .

Эллипс

Определение. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.

Каноническое уравнение эллипса .

у

с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.

и называются фокальными радиусами. ,

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

Определение.Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет – величина, определяемая отношением: .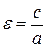

Замечание. Для эллипса .

Определение.Прямые называются директрисами эллипса.

Теорема. Если ­­– расстояние от произвольной точки эллипса до какого-нибудь фокуса, – расстояние от этой же точки до соответствующей этому фокусы директрисы, то отношение есть постоянная величина, равная эксцентриситету эллипса: .

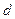
Замечание. Если a = b, то c = 0, а значит, фокусы сливаются, и эллипс превращается в окружность.

Если же 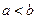, то уравнение определяет эллипс, большая ось которого лежит на оси Оу, а малая ось – на оси Ох. Фокусы такого эллипса находятся в точках F₁ (0;с); F₂(0;-с), где b 2 = a 2 + c 2 .

Пример. Составьте уравнение эллипса, если его фокусы F₁(0; 0), F₂(1; 1), а большая ось равна 2.

Уравнение эллипса имеет вид: .

Расстояние между фокусами: 2c = , таким образом,

a 2 – b 2 = c 2 = .

По условию большая ось равна 2, то есть 2а = 2, откуда получаем, что

а = 1, b = .

Тогда искомое уравнение эллипса имеет вид: .

Гипербола

Определение. Гиперболойназывается линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы .

y

Теорема. Фокусное расстояние и полуоси гиперболы связаны соотношением:

Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы.

Прямоугольник со сторонами 2а и2b называется основным прямоугольником гиперболы.

Гипербола имеет две асимптоты, уравнения которых

Замечание.Для гиперболы эксцентриситет .

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/ε от него, называются директрисами гиперболы. Их уравнения: .

Определение. Гипербола называется равносторонней, если ее полуоси равны ( ).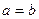

Ее каноническое уравнение .

Определение. Эксцентриситетом гиперболы называется отношение расстояние между фокусами к величине действительной оси гиперболы, обозначается : .

Кривая, определяемая уравнением , также есть гипербола, действительная ось которой расположена на оси , а мнимая ось – на оси .

Гиперболы и имеют общие асимптоты. Такие гиперболы называются сопряженными.

Пример. Составьте уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса, заданного уравнением

Найдем фокусное расстояние для эллипса:

Тогда искомое уравнение гиперболы .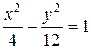

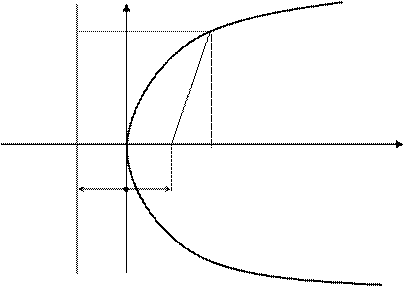
Парабола

Определение. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Каноническое уравнение параболы y 2 = 2px .

у

Линия второго порядка, заданная общим уравнением

Пересечение линии второго порядка и прямой.

Рассмотрим линию второго порядка, заданную общим уравнением
$$
Ax^<2>+2Bxy+Cy^<2>+2Dx+2Ey+F=0\label
$$
в декартовой системе координат, и исследуем пересечение этой линии с произвольной прямой
$$
x=x_<0>+\alpha t,\ y=y_<0>+\beta t.\label
$$
Значения параметра \(t\), соответствующие точкам пересечения, должны удовлетворять уравнению, получаемому подстановкой \eqref в \eqref:
$$
A(x_<0>+\alpha t)^<2>+2B(x_<0>+\alpha t)(y_<0>+\beta t)+C(y_<0>+\beta t)^ <2>+\\+ 2D(x_<0>+\alpha t)+2E(y_<0>+\beta t)+F=0.\label
$$
Раскрывая скобки и приводя подобные члены, мы получим уравнение
$$
Pt^<2>+2Qt+R=0,\label
$$
в котором
$$
P=A\alpha^<2>+2B\alpha\beta+C\beta^<2>,\label
$$
$$
Q=(Ax_<0>+By_<0>+D)\alpha+(Bx_<0>+Cy_<0>+E)\beta,\label
$$
или, при другой группировке слагаемых,
$$
Q=(A\alpha+B\beta)x_<0>+(B\alpha+C\beta)y_<0>+D\alpha+E\beta.\label
$$
Свободный член — это значение многочлена при \(t=0\), то есть
$$
R=Ax_<0>^<2>+2Bx_<0>y_<0>+Cy_<0>^<2>+2Dx_<0>+2Ey_<0>+F=0.\label
$$

Вообще говоря, уравнение \eqref квадратное, имеет не больше двух корней, и прямая пересекает линию или в двух точках, или в одной точке (кратные корни), или не пересекает ее (комплексные корни). Но возможны “исключительные” прямые, для которых \(P=0\), то есть
$$
A\alpha^<2>+2B\alpha\beta+C\beta^<2>=0,\label
$$
и, следовательно, уравнение \eqref является линейным. В этом случае оно имеет один корень при \(Q \neq 0\), а при \(Q=0\) либо выполнено тождественно (если и \(R=0\)), либо не имеет решений. Следовательно, “исключительные” прямые или пересекают линию в единственной точке, или лежат на ней целиком, или не имеют с ней общих точек.

В равенство \eqref не входят координаты начальной точки прямой. Кроме того, оно остается справедливым, если умножить \(\alpha\) и \(\beta\) на общий ненулевой множитель.

Направление, определяемое вектором, компоненты которого удовлетворяют уравнению \eqref, называется асимптотическим направлением линии второго порядка.

Тип линии.

Выясним, сколько асимптотических направлений может иметь линия второго порядка. Обозначив
$$
\delta=\begin
A& B\\
B& C
\end,\nonumber
$$
сформулируем следующее утверждение.

Линия второго порядка имеет два асимптотических направления, если \(\delta 0\).

Рассмотрим несколько случаев.

1. Пусть \(A=C=0\). Тогда \(B \neq 0\) и \(\delta=-B^ <2>0\).
2. Случай \(A \neq 0\) исследуется аналогично случаю 2, только нужно рассматривать не угловой коэффициент, а отношение \(\alpha/\beta\).

Поскольку разобранные выше случаи исчерпывают все возможности, предложение доказано.

От противного нетрудно проверить, что и обратно число асимптотических направлений определяет знак \(\delta\).

Мы определили асимптотические направления при помощи аналитического условия \eqref. Поэтому в принципе при изменении системы координат асимптотическое направление могло бы перестать быть асимптотическим, или, наоборот, обыкновенное направление стать асимптотическим. Из геометрического смысла асимптотических направлений видно, что в действительности асимптотические направления не зависят от выбора системы координат.

Используя канонические уравнения, легко проверить, что эллипс не имеет асимптотических направлений, парабола имеет одно, а гипербола — два асимптотических направления (рис. 9.1). Поэтому линии второго порядка называются линиями гиперболического, параболического или эллиптического типа, смотря по тому, имеют они два, одно или не имеют ни одного асимптотического направления.

Для линий гиперболического типа \(\delta 0\).

Рис. 9.1. Асимптотическое направление.

Диаметр линии второго порядка.

Назовем хордой любой отрезок, концы которого лежат на линии, а остальные точки на ней не лежат. Таким образом, хорда не может иметь асимптотического направления.

Предположим, что рассматриваемая линия второго порядка имеет по крайней мере одну хорду. Этому условию удовлетворяют эллипсы, гиперболы, пары пересекающихся прямых, параболы и пары параллельных прямых.

Фиксируем какое-нибудь неасимптотическое направление и исследуем множество середин хорд, имеющих это направление. Если начальная точка \(M_<0>(x_<0>, y_<0>)\) секущей \eqref находится в середине хорды, то корни уравнения \eqref равны по абсолютной величине и отличаются знаком (рис. 9.2). Это будет так в том и только том случае, когда \(Q=0\). Используя \eqref, мы получаем, что середины хорд направления \((\alpha, \beta)^<2>\) лежат на прямой
$$
(A\alpha+B\beta)x+(B\alpha+C\beta)y+D\alpha+E\beta=0.\label
$$

Рис. 9.2. Хорды.

Прямая \eqref называется диаметром линии второго порядка, сопряженным направлению \((\alpha, \beta)\).

Стоит обратить внимание на то, что диаметром называется вся прямая. Это не означает, что середины хорд заполняют ее целиком. Так может быть, но возможно также, что множество середин хорд есть, например, отрезок или луч.

Конечно, остается сомнение, действительно ли уравнение \eqref определяет прямую: не окажутся ли в нем коэффициенты при переменных оба равными нулю? Допустим, что это так, то есть
$$
A\alpha+B\beta=0,\ B\alpha+C\beta=0.\nonumber
$$

Умножим первое из этих равенств на \(\alpha\), второе — на \(\beta\) и сложим. Мы получим равенство \eqref, которое по предположению не имеет места. Следовательно, уравнение \eqref определяет прямую.

Центр линии второго порядка.

Обозначим левую часть уравнения \eqref через \(\boldsymbol<\Phi>(x, y)\) и введем еще одно понятие.

По-видимому, это определение зависит от выбора системы координат, так как в нем участвует не линия, а многочлен, стоящий в левой части ее уравнения. Допустим, что координаты \(x_<0>, y_<0>\) точки \(O\) в некоторой системе координат удовлетворяют уравнению \eqref. Будут ли ее координаты \((\tilde_<0>, \tilde_<0>)\) в другой системе координат удовлетворять равенству того же вида для многочлена \(\tilde<\boldsymbol<\Phi>>(\tilde, \tilde)\), задающего ту же линию в новой системе координат? Легко видеть, что это так, потому что многочлен \(\tilde<\boldsymbol<\Phi>>\) так и выбирается, чтобы для координат любой точки выполнялось равенство \(\tilde<\boldsymbol<\Phi>>(\tilde, \tilde)=\boldsymbol<\Phi>(x, y)\). Нам остается только выписать это равенство для точек, получаемых из \(O\) сдвигом на векторы \(\boldsymbol\) и \(-\boldsymbol\).

Ниже мы докажем, что в том случае, когда линия содержит хоть одну точку, центры линии и только они являются ее центрами симметрии. Однако понятие центра несколько более общее: линии, являющиеся пустыми множествами, имеют вполне определенные центры, хотя говорить об их центрах симметрии смысла нет. Например, каждая точка прямой \(y=0\) является центром линии с уравнением \(y^<2>+1=0\).

Получим систему уравнений для координат центра. С этой целью напишем подробнее равенство \eqref. Его левая часть равна
$$
A(x_<0>+\alpha)^<2>+2B(x_<0>+\alpha)(y_<0>+\beta) +\\+ C(y_<0>+\beta)^<2>+2D(x_<0>+\alpha)+2E(y_<0>+\beta)+F.\nonumber
$$
Правая часть отличается от левой только знаками у \(\alpha\) и \(\beta\). Поэтому при вычитании \(\boldsymbol<\Phi>(x_<0>-\alpha, y_<0>-\beta)\) из \(\boldsymbol<\Phi>(x_<0>+\alpha, y_<0>+\beta)\) уничтожаются все члены, кроме тех, в которые \(\alpha\) и \(\beta\) входят в первой степени, а члены с первыми степенями удвоятся. После упрощений мы получаем
$$
(Ax_<0>+By_<0>+D)\alpha+(Bx_<0>+Cy_<0>+E)\beta=0.\label
$$

Но равенство \eqref, а вместе с ним и равносильное равенство \eqref имеет место при любых \(\alpha\) и \(\beta\), в частности, при \(\alpha=1\), \(\beta=0\) и при \(\alpha=0\), \(\beta=1\). Отсюда следует, что координаты \((x_<0>, y_<0>)\) центра должны удовлетворять системе уравнений
$$
\left\<\begin
Ax_<0>+By_<0>+D=0,\\
Bx_<0>+Cy_<0>+E=0.
\end\right.\label
$$

Легко видеть, что и обратно, если справедливы равенства \eqref, то, умножая их на произвольные числа \(\alpha\) и \(\beta\) и складывая, мы получим \eqref, а тем самым и \eqref.

Исследуем, обязательно ли существуют центры у линии второго порядка, а если они существуют, то сколько их и как они расположены. Система уравнений \eqref имеет единственное решение тогда и только тогда, когда
$$
\delta=\begin
A& B\\
B& C
\end \neq 0.\label
$$
Таким образом, условие \(\delta \neq 0\) необходимо и достаточно для того, чтобы линия второго порядка имела единственный центр.

Линии второго порядка, имеющие единственный центр, называются центральными.

Полученное условие показывает, что центральными являются линии эллиптического и гиперболического типов.

Условие \(\delta=0\) характеризует нецентральные линии. Это — линии параболического типа. При условии \(\delta=0\) система \eqref либо не имеет решения, либо равносильна одному из составляющих ее уравнений (ранее мы уже доказывали этот факт). Это значит, что нецентральная линия либо не имеет центра (парабола), либо ее центры заполняют прямую линию (пары параллельных прямых, вещественных и мнимых, и пары совпавших прямых).

Если линия второго порядка не является пустым множеством и имеет центр \(O(x_<0>, y_<0>)\), то он — ее центр симметрии.

В самом деле, рассмотрим произвольную точку линии \(M(x, y)\) и докажем, что симметричная ей относительно \(O\) точка \(M_<1>(x_<1>, y_<1>)\) также лежит на линии. Точка \(M_<1>\) определяется равенством \(\overrightarrow>=-\overrightarrow\). Если \((\alpha, \beta)\) — координаты вектора \(\overrightarrow\), то \(x=x_<0>+\alpha\), \(y=y_<0>+\beta\), а \(x_<1>=x_<0>-\alpha\), \(y_<1>=y_<0>-\beta\). Теперь ясно, что в силу \eqref из \(\boldsymbol<\Phi>(x, y)=0\) следует \(\boldsymbol<\Phi>(x_<1>, y_<1>)=0\). Утверждение доказано.

Если линия содержит хотя бы одну точку и имеет центр симметрии \(O(x_<0>, y_<0>)\), то \(O\) является центром.

Рассмотрим пересечение линии с прямой, проходящей через \(O\), приняв эту точку за начальную точку прямой. Имеются две возможности:

1. Точка \(O\) лежит на линии. Пусть прямая имеет неасимптотическое направление. Тогда \(O\) — единственная точка пересечения, так как иначе с учетом симметрии точек пересечения было бы не меньше трех. Следовательно, уравнение \eqref имеет кратный корень \(t=0\), откуда вытекает \(Q=0\). Итак, координаты точки \(O\) удовлетворяют равенству (12) при любых \(\alpha\) и \(\beta\), соответствующих неасимптотическим направлениям. Выберем два различных неасимптотических направления \((\alpha, \beta)\) и \((\alpha’, \beta’)\) и рассмотрим равенства
   $$
   \begin
   & (Ax_<0>+By_<0>+D)\alpha+(Bx_<0>+Cy_<0>+E)\beta=0,\\
   & (Ax_<0>+By_<0>+D)\alpha’+(Bx_<0>+Cy_<0>+E)\beta’=0.
   \end\nonumber
   $$
   как систему уравнений с коэффициентами \(\alpha\), \(\beta\), \(\alpha’\), \(\beta’\), причем \((\alpha\beta’-\alpha’\beta \neq 0)\). Мы получаем равенства \eqref, как и требовалось.
2. Точка \(O\) не лежит на линии. Если прямая пересекает линию в точке \(M\), которой соответствует значение параметра \(t_ <1>\neq 0\), то существует симметричная точка пересечения со значением параметра \(-t_<1>\). Тогда \(Pt_<1>^<2>+2Qt_<1>+R=0\) и \(Pt_<1>^<2>-2Qt_<1>+R=0\), откуда следует \(Q=0\).

Таким образом, если линия имеет точки пересечения с двумя различными прямыми, проходящими через \(O\), то, как и выше, мы можем получить равенства \eqref для координат \(O\). Докажем, что такие прямые обязательно найдутся. Действительно, в противном случае все точки линии лежат на одной прямой. Согласно теореме о существующих типах линий второго порядка линии только двух классов обладают этим свойством: пары совпавших прямых и пары мнимых пересекающихся прямых. Но и для того, и для другого класса все центры симметрии принадлежат линии, что противоречит сделанному предположению. Утверждение доказано.

Сопряженные направления.

Направление \((\alpha’, \beta’)\), определяемое диаметром, сопряженным направлению \((\alpha, \beta)\), называется сопряженным направлению \((\alpha, \beta)\). Компоненты \((\alpha’, \beta’)\), направляющего вектора диаметра \eqref согласно доказанному ранее утверждению 6 удовлетворяют условию
$$
(A\alpha+B\beta)\alpha’+(B\alpha+C\beta)\beta’=0\label
$$
или
$$
A\alpha\alpha’+B(\alpha’\beta+\alpha\beta’)+C\beta\beta’=0\label
$$
В последнее выражение пары чисел \((\alpha, \beta)\) и \((\alpha’, \beta’)\) входят симметричным образом. Поэтому имеет место следующее утверждение.

Если направление \((\alpha’, \beta’)\), сопряженное с \((\alpha, \beta)\), не является асимптотическим, то сопряженным для \((\alpha’, \beta’)\) будет направление \((\alpha, \beta)\) (рис. 9.3).

Рис. 9.3. Сопряженные направления.

Возникает вопрос, при каких условиях направление, сопряженное какому-нибудь направлению \((\alpha, \beta)\) может оказаться асимптотическим. Это легко выяснить. Из равенства \eqref следует, что в качестве \(\alpha’\) и \(\beta’\) можно выбрать соответственно — \(-(B\alpha+C\beta)\) и \((A\alpha+B\beta)\). Подставим это в уравнение \eqref для асимптотических направлений:
$$
A(B\alpha+C\beta)^<2>-2B(B\alpha+C\beta)(A\alpha+B\beta)+C(A\alpha+B\beta)^<2>=0.\nonumber
$$
После преобразований получаем \((AC-B^<2>) \times (A\alpha^<2>+2B\alpha\beta+C\beta^<2>)=0\). Поскольку исходное направление не асимптотическое, это произведение может обратиться в нуль только за счет первого сомножителя. Мы получаем новое утверждение.

Если линия не центральная \((\delta=0)\), то для любого направления \((\alpha, \beta)\) сопряженное направление — асимптотическое (рис. 9.4). Если линия центральная \((\delta \neq 0)\), то направление, сопряженное любому направлению, не асимптотическое.

Рис. 9.4. Сопряженные направления у параболы.

Главные направления.

Если диаметр перпендикулярен хордам, которым он сопряжен, то он является осью симметрии рассматриваемой линии.

Направление \((\alpha, \beta)\) и направление \((\alpha’, \beta’)\) сопряженного ему диаметра называются главными направлениями, если они перпендикулярны.

Если система координат декартова прямоугольная, то для главного направления компоненты \((\alpha, \beta)\) должны быть пропорциональны коэффициентам уравнения \eqref, то есть должно существовать такое число \(\lambda\), что
$$
A\alpha+B\beta=\lambda\alpha,\ B\alpha+C\beta=\lambda\beta.\label
$$
Исключая \(\lambda\), мы получаем уравнение для \(\alpha\) и \(\beta\):
$$
(A-C)\alpha\beta+B(\beta^<2>-\alpha^<2>)=0.\label
$$

Если положить \(\alpha=\cos \varphi\), \(\beta=\sin \varphi\), то уравнение \eqref превратится в уравнение \(2B \cos 2\varphi = (A-C)\sin 2\varphi\), которое, как мы видели, обязательно имеет решение относительно \(\varphi\). Поэтому имеет место следующее утверждение.

Каждая линия второго порядка имеет хотя бы одну пару главных направлений.

Более подробное исследование уравнения \eqref показывает, что либо эта пара единственная, либо каждая пара перпендикулярных направлений является главной. Последний случай имеет место, когда \(A=C\), \(B=0\). При этом уравнение линии приводится к одному из канонических видов: \(x^<2>+y^<2>=a^<2>\), \(x^<2>+y^<2>=-a^<2>\) или \(x^<2>+y^<2>=0\). В двух последних случаях линия не имеет хорд, и результат лишен геометрического смысла.

Касательная к линии второго порядка.

Как известно, касательной к какой-либо линии называется предельное положение секущей, когда хорда стягивается в точку. Выведем уравнение касательной к линии второго порядка, заданной уравнением \eqref. Дадим предварительно следующее определение.

Особой точкой линии второго порядка называется ее центр, который лежит на линии.

Особыми точками являются: точка пересечения пары пересекающихся прямых, единственная точка пары мнимых пересекающихся прямых и каждая точка пары совпавших прямых. В особой точке касательная не определена. Если точка лежит на прямой, входящей в состав линии, то касательная в этой точке совпадает с прямой. Исключив эти случаи, мы фактически ограничиваемся рассмотрением касательных к эллипсам, гиперболам и параболам.

Рассмотрим точку \(M_<0>(x_<0, y_<0>>)\), лежащую на линии \(L\), и прямую с начальной точкой \(M_<0>\), заданную уравнением \eqref. С нашей точки зрения, приведенное выше определение касательной означает, что уравнение \eqref, определяющее точки пересечения \(L\) и прямой, имеет два совпадающих корня.

Так как начальная точка принадлежит \(L\), в уравнении \eqref \(R=0\), и один из его корней равен нулю. Корни совпадают, если и второй корень равен нулю, для чего необходимо, чтобы \(Q=0\). Если при этом окажется, что и \(P=0\), то прямая принадлежит линии второго порядка. Этот случай мы исключили, и потому уравнение имеет кратный корень \(t=0\) в том и только том случае, когда \(Q=0\). Мы рассматриваем равенство \(Q=0\) как условие, определяющее направляющий вектор касательной:
$$
(Ax_<0>+By_<0>+D)\alpha+(Bx_<0>+Cy_<0>+E)\beta=0.\label
$$

Так как \(M_<0>\) не особая точка, обе скобки здесь одновременно в нуль не обращаются, и условие \eqref определяет \(\alpha\) и \(\beta\) с точностью до общего множителя. Точка \(M(x, y)\) лежит на касательной тогда и только тогда, когда вектор \(\overrightarrowM>\) коллинеарен \(\boldsymbol(\alpha, \beta)\), то есть его координаты \(x-x_<0>\) и \(y-y_<0>\) удовлетворяют тому же условию, что и \((\alpha, \beta)\):
$$
(Ax_<0>+By_<0>+D)(x-x_<0>)+(Bx_<0>+Cy_<0>+E)(y-y_<0>)=0.\label
$$

Это и есть уравнение касательной к линии \(L\) в точке \(M_<0>\), лежащей на линии. Уравнение \eqref можно записать и иначе, если заметить, что координаты \(M_<0>\) удовлетворяют уравнению \eqref и, следовательно,
$$
(Ax_<0>+By_<0>+D)x_<0>+(Bx_<0>+Cy_<0>+E)y_<0>+Dx_<0>+Ey_<0>+F=0.\nonumber
$$
Прибавляя это равенство к \eqref и группируя слагаемые, получим окончательное уравнение
$$
Axx_<0>+B(xy_<0>+x_<0>y)+Cyy_<0>+D(x+x_<0>)+E(y+y_<0>)+F=0.\label
$$

Особые точки.

Напомним, что особая точка линии второго порядка — это ее центр, лежащий на линии. Исследуем, при каких условиях линия второго порядка имеет особую точку. Для координат \((x_<0>, y_<0>)\) особой точки должны быть справедливы равенства
$$
\begin
& Ax_<0>+By_<0>+D=0,\ Bx_<0>+Cy_<0>+E=0,\\
& Ax_<0>^<2>+2Bx_<0>y_<0>+Cy_<0>^<2>+2Dx_<0>+2Ey_<0>+F=0.
\end\nonumber
$$
Умножим первое из них на \(x_<0>\), второе на \(y_<0>\) и вычтем из третьего. Мы получим эквивалентную систему уравнений
$$
\left\<\begin
Ax_<0>+By_<0>+D=0,\\
Bx_<0>+Cy_<0>+E=0,\\
Dx_<0>+Ey_<0>+F=0.
\end\right.\label
$$
Выберем какой-нибудь базис в пространстве и рассмотрим вспомогательные векторы \(\boldsymbol

(A, B, D)\), \(\boldsymbol(B, C, E)\) и \(\boldsymbol(D, E, F)\). Равенства \eqref представляют собой координатную запись векторного равенства
$$
x_<0>\boldsymbol

+y_<0>\boldsymbol=-\boldsymbol.\label
$$
Отсюда следует, что при наличии особой точки векторы \(\boldsymbol

\), \(\boldsymbol\) и \(\boldsymbol\) компланарны, и потому
$$
\triangle=\begin
A& B& D\\
B& C& E\\
D& E& F
\end=0.\label
$$

Если линия центральная, то векторы \(\boldsymbol

\) и \(\boldsymbol\) не коллинеарны, и условие компланарности \eqref равносильно существованию разложения \eqref, то есть существованию решения системы \eqref. Мы получили ещё одно утверждение.

Центральная линия имеет особую точку тогда и только тогда, когда \(\triangle=0\).

Итак, сочетание \(\delta 0\), \(\triangle=0\) — пары мнимых пересекающихся прямых.

Рассмотрим нецентральные линии. Для них существует центр, хотя бы не являющийся особой точкой, тогда и только тогда, когда \(\triangle=0\). В этом (и только этом) случае векторы \(\boldsymbol

\) и \(\boldsymbol\) коллинеарны. Действительно, так как \(\delta=0\), по предложению 9 § 2 гл. II, если система уравнений \eqref имеет решение, она равносильна одному из составляющих ее уравнений: либо коэффициенты и свободный член одного из уравнений равны нулю, либо коэффициенты и свободные члены обоих уравнений пропорциональны. Тогда \(\triangle=0\) независимо от \(\boldsymbol\).

Обратно, пусть для нецентральной линии \(\triangle=0\). Докажем, что \(\boldsymbol

\) и \(\boldsymbol\) коллинеарны, что равносильно совместности уравнений центра. Действительно, в противном случае \(\boldsymbol\) по ним раскладывается, и согласно \eqref существует особая точка. Она — центр, \(\boldsymbol

\) и \(\boldsymbol\) коллинеарны, и мы получаем противоречие.

Для нецентральных линий условие \(\triangle=0\) равносильно существованию центра.

Итак, сочетание \(\delta=\triangle=0\) характеризует пары параллельных прямых (вещественных, мнимых или совпавших).

Из последних двух утверждений следует, что равенство \(\triangle=0\) является инвариантным: оно не может измениться при переходе к другой системе координат.

2.6 Общее уравнение 2-го порядка, типы линий

Напомним, что общее уравнение 2-го порядка имеет вид

(2.13)

Т. е. хотя бы один из коэффициентов А, В или С отличен от нуля. Здесь функция двух переменных

Называется квадратичной формой, а матрица называется матрицей квадратичной формы. Она симметрична, так как совпадают элементы, симметрично расположенные относительно главной диагонали. Определитель этой матрицы D = AC – B2 – это величина, знак которой, а также знаки коэффициентов А и С Играют решающую роль при выяснении вопроса о типе кривой, заданной общим уравнением. Функция двух переменных

Называется линейной функцией. Таким образом, левая часть уравнения (2.13) есть сумма двух слагаемых:

Квадратичная форма + линейная функция.

Какие кривые на плоскости определяются алгебраическим уравнением (2.13) с условием (2.14)? Во-первых, это может быть одна из трех рассмотренных нами кривых второго порядка: эллипс, гипербола или парабола (эллипс и гипербола – центральные кривые, имеют центр симметрии, парабола – не имеет центра симметрии). Кроме того, уравнение (2.13) может определять некоторые вырожденные кривые:

А) пара пересекающихся прямых, например:

В) пара параллельных прямых, например:

С) пара совпадающих прямых, например:

D) «вырожденный» эллипс – точка, например:

X2 – 2X + Y2+ 1 = 0, (X – 1)2 + Y2 = 0,

Е) пустое множество:

В курсе аналитической геометрии доказывается, что других возможностей, кроме перечисленных, быть не может. При таких преобразованиях системы координат, как параллельный сдвиг и поворот осей, определитель матрицы квадратичной формы D = AC – B2 не меняется, и с его помощью линии второго порядка классифицируют по следующим трем типам: