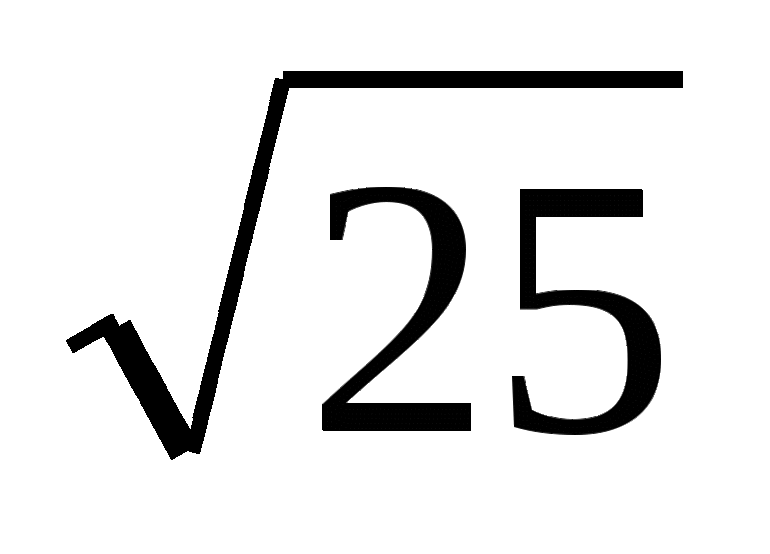Урок по теме «Методы решения задач с параметрами»
Разделы: Математика
Цель данной работы – изучение различных способов решения задач с параметрами. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность. Для развития этих навыков необходимы длительнее усилия, именно поэтому в профильных 10-11 классах с углубленным изучением точных наук введен курс: “Математический практикум”, частью которого является решение уравнений и неравенств с параметрами. Курс входит в число дисциплин, включенных в компонент учебного плана школы.
Успешному изучению методов решения задач с параметрами могут помочь элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с параметрами”.
Рассмотрим четыре больших класса задач с параметрами:
- Уравнения, неравенства и их системы, которые необходимо решить для любого значения параметра, либо для значений параметра, принадлежащих определенному множеству.
- Уравнения, неравенства и их системы, для которых требуется определить количество решений в зависимости от значения параметра.
- Уравнения, неравенства и их системы, для которых требуется найти все те значения параметра, при которых указанные уравнения (системы, неравенства) имеют заданное число решений.
- Уравнения, неравенства и их системы, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Методы решений задач с параметрами.
1. Аналитический метод.
Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.
Пример 1. Найдите все значения параметра a, при которых уравнение:
(2a – 1)x 2 + ax + (2a – 3) =0 имеет не более одного корня.
При 2a – 1 = 0 данное уравнение квадратным не является, поэтому случай a =1/2 разбираем отдельно.
Если a = 1/2, то уравнение принимает вид 1/2x – 2 = 0, оно имеет один корень.
Если a ≠ 1/2 , то уравнение является квадратным; чтобы оно имело не более одного корня необходимо и достаточно, чтобы дискриминант был неположителен:
Чтобы записать окончательный ответ, необходимо понять,
2. Графический метод.
В зависимости от задачи (с переменной x и параметром a) рассматриваются графики в координатной плоскости (x;y) или в плоскости (x;a).
Пример 2. Для каждого значения параметра a определите количество решений уравнения 
Заметим, что количество решений уравнения 

График функции 
y = a – это горизонтальная прямая. По графику несложно установить количество точек пересечения в зависимости от a (например, при a = 11 – две точки пересечения; при a = 2 – восемь точек пересечения).
Ответ: при a 25/4 – два решения.
3. Метод решения относительно параметра.
При решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.
Пример 3. Найти все значения параметра а , при каждом из которых уравнение 
Будем решать это уравнение заменой переменных. Пусть 
1) Если а = 0, то уравнение имеет единственное решение t = 2.
Решение некоторых типов уравнений и неравенств с параметрами.
Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности.
Решение каждой задачи своеобразно и требует к себе индивидуального, нестандартного подхода, поскольку не существует единого способа решения таких задач.
Задача № 1. При каких значениях параметра b уравнение 
Ⅱ . Степенные уравнения, неравенства и их системы.
Задача №2. Найти все значения параметра a, при которых множество решений неравенства:


Преобразуем обе части неравенства.
Для того, чтобы множество решений неравенства содержало число 6, необходимо и достаточно выполнение условия:

При a > 6 множество решений неравенства: 
Интервал (0;5) не может содержать ни одного отрезка длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в интервале (5; a).
Это
Ⅲ . Показательные уравнения, неравенства и системы.
Задача № 3. В области определения функции 
1) Графиком дробно-линейной функции 

2) По определению степени область определения D(y) состоит из решений неравенства 
3) При 0 0 , то z(x) > z(0) = 1 . Значит, каждое положительное значение х является решением неравенства 
4) При a > 1 показательная функция с основанием а возрастает и неравенство 



Решение иррациональных уравнений и неравенств, а также уравнений, неравенств и систем, содержащих модули рассмотрены в Приложении 1.
Задачи с параметрами являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа.
По статистике многие из выпускников не приступают к решению задач с параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению таких задач, и процент их верного решения невысок: 2–3%, поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе задач с параметрами, учащимися школ по-прежнему остается актуальным.
Методы решения задач с параметрами
Задачи с параметрами являются одним из самых трудных разделов школьного курса математики, так как их решение связано с умением проводить сложные, разветвленные логические построения. В школе первые представления о параметре мы получаем при изучении прямой пропорциональности; линейной функции и линейного уравнения; при изучении квадратного уравнения и исследования количества его корней в зависимости от значений параметра.
Скачать:
| Вложение | Размер |
|---|---|
| ekhlakov_daniil_gotovy_variant.ppt | 1.57 МБ |
| ekhlakov_daniil.docx | 152.63 КБ |
Предварительный просмотр:
Подписи к слайдам:
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ Автор работы: Ехлаков Д. Н. 10 класс Лицей МГУ им. Н. П. Огарева Руководитель работы: Кубанцева А. В. учитель математики Лицей МГУ им Н. П. Огарева Лицей федерального государственного бюджетного образовательного учреждения высшего образования «Национальный исследовательский Мордовский государственный университет им. Н.П. Огарёва» Саранск, 2021 Секция: Научно-исследовательская работа Направление: Естественные науки
Актуальность темы: Статистика решения задачи №18 на ЕГЭ по профильной математике Цель работы: исследование методов решения задач с параметрами и выявление наиболее рациональных, наименее трудоемких способов решения. Задачи: 1. Познакомится с определением параметра и видами задач, содержащие параметры; 2. Исследовать способы решения задач с параметрами и постараться выбрать из них для себя самые оптимальные; 3. Приобрести опыт в решении задач, содержащиеся в ЕГЭ по профильной математике. Год Проверяемые требования Уровень сложности задания Максимальный балл за выполнение задания Средний процент выполнения 2017 Умение решать уравнения и неравенства, содержавшие параметр Высокий уровень сложности 4 0,38 2018 1,2 2019 4,8 2020 2,4 Гипотеза: существуют общие методы решения заданий с параметрами, позволяющие решать задания разных видов. Объект исследования : задания контрольно-измерительных материалов единого государственного экзамена по математике, содержащие параметр. Предмет исследования : методы решения заданий с параметрами. Методы исследования – теоретический анализ и синтез научной и учебной литературы по теме исследования, сравнение, систематизация информации, обобщение, вывод, подбор и решение задач. Практическая значимость – возможность использования обобщенных данных при подготовке выпускников к сдаче единого государственного экзамена по математике профильного уровня, отработка решения задач, содержащих параметры.
Основные типы задач с параметрами: Тип 1. Задачи, которые необходимо решить для всех значений параметра или для значений параметра из заданного промежутка. Тип 2. Задачи, где требуется найти количество решений в зависимости от значения параметра. Тип 3. Задачи, где необходимо найти значения параметра, при которых задача имеет заданное количество решений . Тип 4. Задачи, в которых необходимо найти значения параметра, при которых множество решений удовлетворяет заданным условиям.
Основные методы решения задач с параметрами: Аналитический. Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Графический. В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a). Решение относительно параметра. Переменные x и a принимаются равноправными и выбирается та, относительно которой аналитическое решение признается более простым. Аналитический метод Графический метод Метод решения относительно параметра Метод оценки Метод мажорант Метод симметричных корней Методы решения задач с параметрами:
Структура решения задач с параметром Приемы решения задач с параметром графическим методом В координатной плоскости (хОу) В координатной плоскости (хОа) 1. Строим график функции у=f(х;а), задающий семейство кривых, зависящих от параметра а. 2. Определяем преобразование, позволяющее перейти от одной кривой семейства к другой. 3. Читаем график и находим необходимый графический образ . 1. Записываем уравнение F(x;a) = 0 в виде а = f (x) и строим график этой функции. 2. Находим точки пересечения графика функции a = f(x) с прямыми вида a = a0, параллельными оси Ох. 3. Выбираем абсциссы точек пересечения, определяющие решения в соответствии с условием задачи. « … 10 из 100 математиков мыслят формулами… Но остальные мыслят образами; их интуиция геометрическая. Картинки несут гораздо больше информации, чем слова. В течение многих лет школьников отучали пользоваться картинками, потому что «они не строгие»… Да, они не строгие, но они помогают думать, а такого рода помощью никогда не следует пренебрегать» Ян Стюарт Аналитический метод решения задач с параметрами Задачи, в которых расположение корней квадратного трехчлена относительно точки с абсциссой Условие а ˃0 обеспечивает положительный коэффициент перед х 2 (направленность ветвей параболы вверх); Условие f ( m )˂0 обеспечивает: наличие корней квадратного трехчлена; расположение точки m между корнями. Условие а ˃ 0 обеспечивает положительный коэффициент перед х 2 ; Условие f (m) ˃ 0 обеспечивает расположение точки m вне отрезка между корнями; Условие D ˃ 0 обеспечивает наличие корней уравнения; Условие х 0 ˃ m обеспечивает расположение точки m левее отрезка между корнями. Условие a ˃ 0 обеспечивает положительный коэффициент перед х 2 ; Условие f (m) ˃ 0 обеспечивает расположение точки m вне отрезка между корнями; Условие D ˃ 0 обеспечивает наличие корней уравнения; Условие х 0 ˂ m обеспечивает расположение точки m правее отрезка между корнями. оба корня меньше m ; один корень меньше m , а другой больше; оба корня больше m . корни квадратного трехчлена справа от отрезка; Условие f (p) ˃ 0 обеспечивает нахождение корней вне отрезка между корнями; Условие D ˃ 0 обеспечивает наличие двух корней квадратного трёхчлена; Условие x 0 ˃ p обеспечивает расположение отрезка левее абсциссы вершины. Условие f (m) ˃ 0 обеспечивает нахождение корней вне отрезка между корнями; Условие D ˃ 0 обеспечивает наличие корней уравнения; Условие x 0 ˂ m обеспечивает расположение отрезка m правее отрезка между корнями. Условие f (m) ˂ 0 обеспечивает расположение точки m внутри отрезка между корнями; Условие f (p) ˃ 0 обеспечивает расположение корней вне отрезка между корнями. Условие f (p) ˂ 0 обеспечивает расположение точки p внутри отрезка между корнями; Условие f (m) ˃ 0 обеспечивает расположение точки m вне отрезка между корнями. Условие f (m) ˃ 0 обеспечивает расположение точки m вне отрезка между корнями; Условие f (p) ˃ 0 обеспечивает расположение точки p вне отрезка между корнями; Условие D ˃ 0 обеспечивает наличие корней уравнения; Условие m ˂ x 0 ˂ p обеспечивает расположение вершины параболы между концами отрезка. Условие f (p) ˂ 0 обеспечивает расположение точки p внутри отрезка между корнями; Условие f (m) ˂ 0 обеспечивает расположение точки m вне отрезка между корнями. корни квадратного трехчлена слева от отрезка; больший корень внутри отрезка; меньший корень внутри отрезка; оба корня внутри отрезка; отрезок между корнями квадратного трехчлена. Задачи, в которых расположены корни квадратного трехчлена относительно отрезка
Найдите все значения а, для каждого из которых уравнение 25х – (а + 6) · 5 х = (5 + 3 | а |) · 5 х – (а + 6) (3 | а | + 5) имеет единственное решение. 25 х – (а + 6) · 5 х = (5 + 3 | а |) · 5 х – (а + 6) (3 | а | + 5) ; 25 х – (а + 6) · 5 х _ (5 + 3 | а |) · 5 х – (а + 6) (3 | а | + 5) = 0; 25 х – (а + 6 + 5 + 3 | а |) · 5 х + (а + 6) (3 | а | + 5) = 0; Пусть 5 х = t ˃ 0, тогда: t – (а + 6 + 5 + 3 | а |) · t + (а + 6) (3 | а | + 5) = 0; (*) Исходное уравнение будет иметь единственное решение: 1 случай: если уравнение (*) имеет единственное решение ( D = 0); 2 случай: если уравнение (*) имеет два корня ( D ˃ 0), Один из которых меньше нуля или равен нулю. Пусть n = a + 6, m = 5 + 3 | а | ; 1 случай: D = (n + m) 2 – 4mn = 0 → n 2 + 2mn + m 2 – 4mn = 0 → n 2 — 2mn + m 2 = 0 (n – m) 2 = 0 → a + 6 = 5 + 3 | а | → a — 3 | а | = -1 ; Преобразуем исходное уравнение: 25 х – (а + 6) · 5 х = (5 + 3 | а |) · 5 х – (а + 6) (3 | а | + 5) ⟹ 5 х ( 5 х – а – 6) = (5 + 3 | а |) – ( 5 х – а – 6); ⟹ ( 5 х – а – 6) ( 5 х – 3 | а | 5 х – 5 ) = 0 ⟹ 5 х – а – 6 = 0 или 5 х – 3 | а | — 5 =0. На чертеже заметим, что система имеет единственное решение при а = а 1 , а = а 2 и а ≤ — 6. Найдем а 1 и а 2 : Если а ˃ 0, то Если а ˂ 0, то
Предварительный просмотр:
Научно-образовательный форум школьников Республики Мордовия
Лицей федерального государственного бюджетного образовательного учреждения высшего образования «Национальный исследовательский Мордовский государственный университет им. Н.П. Огарёва»
Уравнения с параметром — алгоритмы и примеры решения
Общие сведения
Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.
Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.
Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.
Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.
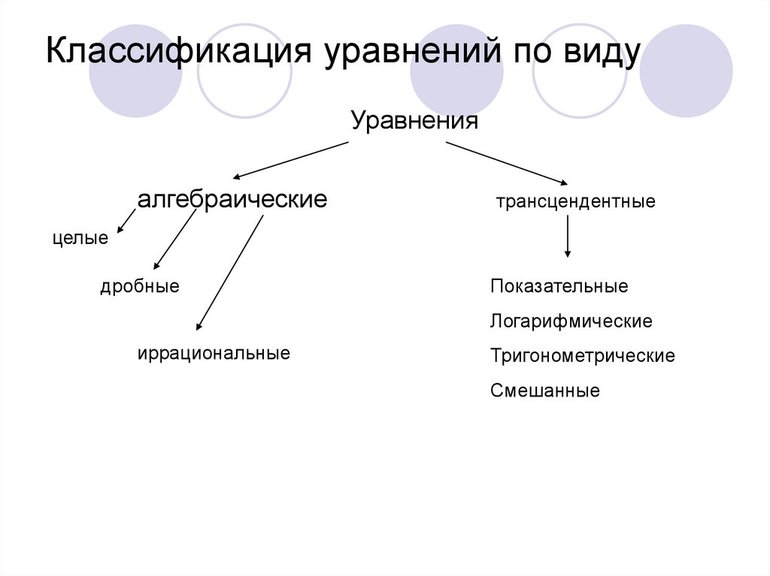
Классификация уравнений
Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».
Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.
Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.
К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.
Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.
Алгебраический вид
Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.
На основании последней характеристики они делятся на 5 типов:
- Линейные.
- Квадратные (квадратичные).
- Кубические.
- Биквадратные.
- Высших порядков.
Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.
Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.
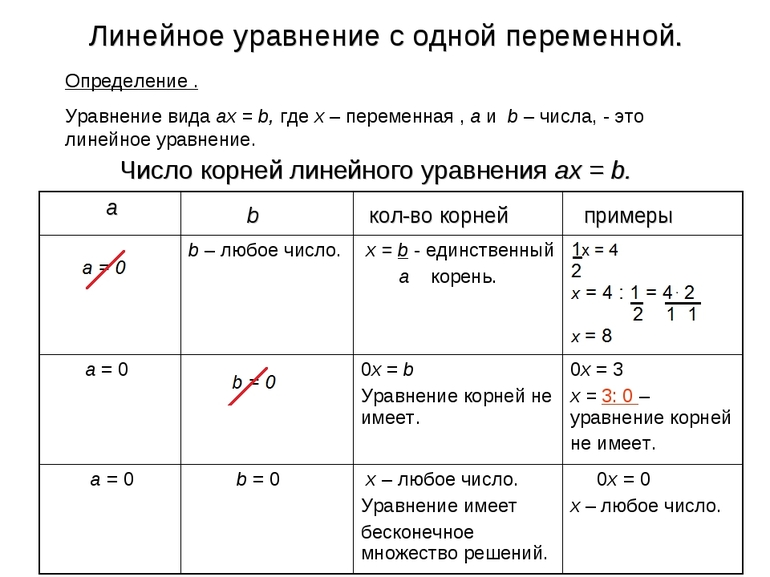
Линейные и квадратичные
Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:
- Записывается искомое выражение.
- При необходимости раскрываются скобки и приводятся подобные элементы.
- Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
- Правая часть сокращается на коэффициент при неизвестной.
- Записывается результат.
- Выполняется проверка посредством подстановки корня в исходное выражение.
Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.
Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:
- Записать выражение.
- Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
- Вычислить значение D (D 0 — два решения).
- При D=0 формула корня имеет такой вид: t=-В/(2А).
- Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
- Записать результат.
- Выполнить проверку по отсеиванию ложных корней.
Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.
Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.
Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.
Кубичеcкие и биквадрaтные
Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.
Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:
- Приводятся подобные элементы: 3v=0.
- Находится корень: v=0.
- Приравнивается к выражению, которое заменяли: t 3 −2=0.
- Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
- Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).
Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:
- Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
- Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
- Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
- Результат: m1=-3 и m2=3.
- Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).
Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.
Пример решения
На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:
- Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
- Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
- Ввести замену v 4 −16=m: m+4p+4=0.
- Вывести формулу нахождения параметра: р=-(m/4)-1.
- Подставить величину m: р=-1-(v 4 +16)/4.
- C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
- Корни: v1=[12]^(¼) и v2=-[12]^(¼).
- Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
- Результат: v1=[12]^(¼).
- Проверка: <[12]^(¼)>^4−16+4=16−16=0 (истина).
Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.
Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.
http://nsportal.ru/ap/nauchno-tehnicheskoe-tvorchestvo/library/2021/11/14/metody-resheniya-zadach-s-parametrami
http://nauka.club/matematika/algebra/uravneniya-s-parametrom.html