Общие принципы построения регрессионных уравнений

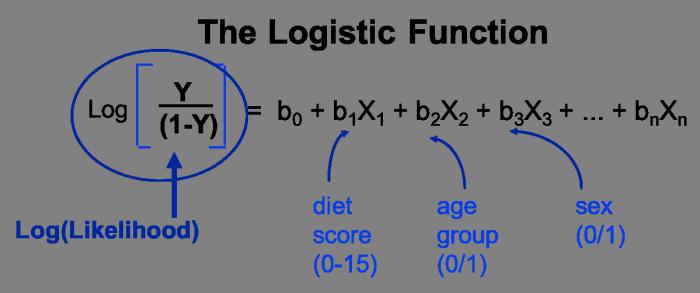
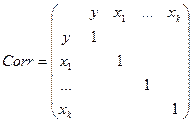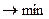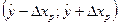Общая методика построения регрессионного уравнения

1) Выбираем зависимую переменную Y.

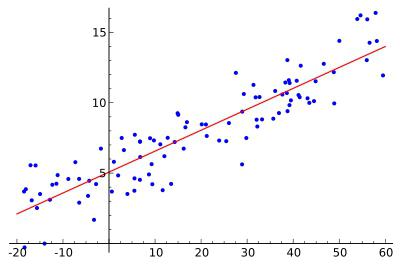
2) Рассматриваем парные графики зависимостей Y от 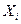, где , k – параметр.

По виду этого графика делаются выводы о наличии или отсутствии зависимости и о виде этой зависимости.

3) Рассматривается матрица корреляции между зависимой переменной и независимой.

Интерпретируются знаки линейной корреляции и сила линейной связи.

Если 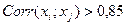, то один из них исключается

4) С помощью метода пошагового отбора строим регрессию (Y, )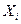

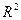
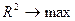
5) Подбираем спецификацию модели, а именно максимизируя , минимизируется количество параметров линейной регрессии.

, количество параметров регрессии

Подбирая спецификацию модели можно использовать следующие соображения:

а) lnY, тогда зависимая переменная не уйдет в минус и зависимость Y от X постепенно, т.е. при изменении параметра X на 1, Y меняется в процентах.

б) берется параметр в квадрате, если с увеличением X его влияние на Y возрастает.

в) ln параметра. В этом случае с ростом значения параметра, влияние на Y уменьшается.

г) использование взаимодействия параметров, например их перемножение.

6) Построение прогноза (точного) наилучшей подобранной модели

7) Построение интервального прогноза, т.е. построение

8) (Дополнительно) Работа с выбросами.

После их удаления п.4-п.7 и сравниваются.

9) Интерпретация полученных результатов:

а) описание экономического смысла модели

б) интерпретация коэффициентов и знаков перед ними

в) анализ точности прогнозирования и ширины интервала

г) описание выбросов

Раздел II

Анализ силы связи порядковых и категориальных переменных

Количественные (или номинальные) переменные – переменные, выражающиеся в числах в определенных единицах измерения.

Категориальные переменные – это переменные, принимающие конечное число значений, состоящих из категорий, которые неупорядочены относительно друг друга. Чаще всего выражаются не в числах.

Например: цвет, уровень образования, страна, фамилия.

Порядковые переменные – это категориальные переменные, для которых определено отношение порядка, т.е. они ранжированы относительно друг друга.

Например: оценка успеваемости, номер места на соревнованиях или группы людей по возрастам. В исследовании социально-экономических явлений часто возникает необходимость оценить силу связи между категориальными и порядковыми переменными. Коэффициент корреляции Пирсона, который считали ранее, не подходит, он не показывает реального состояния. Необходимо использовать другие коэффициенты связи.

Пример: Пусть у нас имеется лекарство и мы хотим проверить есть ли связь между приемом этого лекарства и состояния больного.

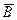x1 x2	В		Итого по строке
А	n11	n12	n10
Ā	n21	n22	n20
Итого по стобцу	n01	n02	N

Всех больных случайным образом делят на 2 группы. 1-ю группу лечат новым препаратом, а 2-ю группу лечат традиционными методами. Таким образом мы получаем 2 показателя: 1-ый показатель: проходил ли больной курс лечения новым препаратом.

Х₁: А – давали лекарство

Х₂ – результат лечения.

Х_2: В – состояние улучшилось

В – состояние ухудшилось

Результаты этого опыта можно представить в таблице.

n11 – число людей, которым давали лекарство и чье состояние улучшилось.

n12 — число людей, которым давали лекарство и чье состояние ухудшилось.

Задача состоит в том, чтобы по этим 4-м числам определить, связан ли результат лечения с приемом лекарства и как именно связан.

Рассмотрим разные варианты.

1.Если между Х1 и Х2 нет никакой связи, лекарство бессмысленно. Тогда доля принимавших лекарство среди больных, чье состояние улучшилось должна быть равна доле принимавших лекарство среди тех, кому стало хуже и равна доле принимавших лекарство среди всех больных.

Доля принимающих лекарство, чье состояние улучшилось=n11/n01

Доля принимающих лекарство, чье состояние ухудшилось=n12/n02

Доля принимавших лекарство среди всех участвующих в эксперименте=n11/n01+n12/n02=n10/N

N11=(n11+n12)(n22+n21)/N – то связи нет!

На равенстве долей и построена мера связи. За меру связи можно принять величину n11=…, но у этой величины значения могут быть и больше 1 и меньше 1 по модулюÞ ее необходимо модифицировать, чтобы сделать похожей на коэффициент корреляции. А именно ввести коэффициент Юла, равный D=(n11n22 — n12n21)/(n11n22+n12n21)

Если D=0, то связи нет.

Если связь сильная отрицательная, то коэффициент Юла D=-1

Если связь сильная положительная, то D=1

Замечание: Коэффициент Юла подходит, если рассматривается таблица 2*2. Т.е. определяется сила связи между 2-мя параметрами, каждый из которых принимает только 2 значения.

Связь считается подтвержденной, если ‌‌׀D׀>0,5.

Пример 1.

B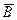
A	n11	n12
Ā	n22

D=(n11n22-0)/(n11n22+0)=1, т.е. из нелечения Þухудшение состояния.

Пример 2.

D=(0-n12n21)/(0+n12n21)=-1, т.е. из лечения Þухудшение самочувствия или если не лечили, то обязательно стало лучше.

Однако часто в маркетинговых исследованиях приходится сталкиваться с ситуацией, когда 1 или оба признака принимают несколько значений.

В этом случае рассчитать коэффициент Юла не получится и следует использовать другие коэффициенты.

Примером таблиц n*m может служить анализ результатов выборок кандидатов в разных регионах страны. Тогда каждому региону сопоставляют столбец, а каждому кандидату – строку.

В таблице стоят значения рейтинга кандидата в соответствующем регионе. Требуется установить связь между регионом и рейтингом в нем кандидатов. Рассмотрим различия статистики тесноты связи: 1. Фи – коэффициент. Его используют для таблиц 2*2.

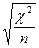
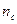
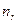
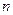
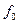
Фи= , где

— итоговое число в столбце

— итоговое число в строке

— полный размер выборки

— соответствующее число в таблице

Ф – коэффициент принимающий значение, равное 0, если связь присутствует, и 1, если связь сильная.

Пример. Найти связь между использованием Интернета и полом.

Общие принципы построения регрессионных уравнений

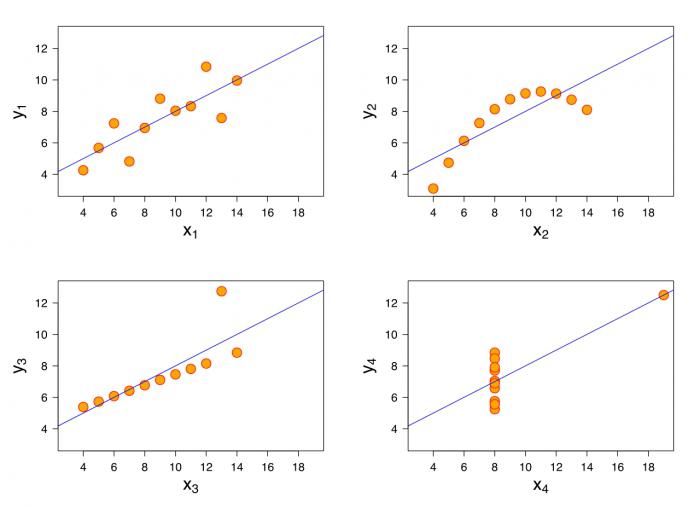
На рисунке 2 приведены примеры корреляционного поля и формы связи, образованные скоплениями точек. Точки группируются возле некоторой линии, если связь показателей линейна, или кривой, если связь нелинейна. Эти линии называются линиями регрессии, а описывающие их аналитические выражения ¾ уравнениями регрессии (рис. 2).

Рис. 2. Формы связи: а ¾ линейная связь; б ¾ параболическая связь; в ¾ гиперболическая связь; г ¾ нет связи (если две переменные практические не связаны между собой, то моделью будет являться горизонтальная прямая)

Зная уравнение регрессии, можно приближенно оценить значение зависимой переменной Y при определенном значении Х. Причем точность такой оценки будет тем выше, чем теснее группируются точки фактических наблюдений относительно линии регрессии, т. е. точность модели регрессии определяется тем, насколько тесной является взаимозависимость признаков Х и Y.

Регрессионный анализ ¾ это статистический метод исследования зависимости случайной величины Y от переменных Х_j.

При построении парной регрессии (с одной факторной переменной) обычно используются следующие функции:

1) линейная

2) степенная

3) показательная

4) параболическая

5) гиперболическая

6) логарифмическая

где а₀ ¾ свободный коэффициент уравнения регрессии;

а₁¾ параметр уравнения регрессии.

Однако в действительности любой результативный показатель испытывает воздействие не одного, как в случае парной корреляции, а нескольких факторов, поэтому зачастую строят модели множественной регрессии, которые принимают вид:

(наиболее часто встречающаяся модель);

где а₀¾ свободный коэффициент регрессии;

а_j (j = 1, 2, …, k) ¾ параметры регрессионного уравнения, называемые коэффициентами регрессии.

Для того чтобы правильно выбрать тип регрессионного уравнения, следует знать условный закон распределения зависимой переменной Y. На основе графика не всегда удается определить его однозначно, поэтому строят несколько регрессионных моделей, а затем по определенным критериям определяют лучшую модель. Если в проводимом исследовании можно ограничиться построением линейной модели, выбирают ее. Такая популярность и предпочтительность объясняется очень просто: математический аппарат линейных уравнений наиболее разработан, а сами модели легко интерпретируемы.

Критерием нахождения значений коэффициентов регрессии а_j является следующее требование: сумма квадратов отклонений наблюдаемых «игреков» от «игреков», рассчитанных по уравнению регрессии, должна быть минимальной. Параметры регрессионной модели должны быть такими, чтобы на графике корреляционного поля линия регрессии оказалась там, где точки фактических наблюдений наибольшим образом сконцентрированы, т. е. проходила бы на минимальном удалении от них. В виде формулы это требование записывается следующим образом:

Метод нахождения значений коэффициентов регрессии по приведенному критерию называется методом наименьших квадратов(МНК).

Уравнение регрессии. Уравнение множественной регрессии

Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.

Определение понятия регрессии

В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).

Какие бывают типы связей между переменными

В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.

Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.

Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.

Виды регрессий

На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.

Гиперболическая, линейная и логарифмическая

Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.

Множественная и нелинейная

Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х₁ , х₂ . х_с)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.

Обратные и парные виды регрессий

Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.

Понятие корреляции

Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.

Методы

Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.

Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.

В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.

Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).

Корреляция для множественной регрессии

Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.

Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.

Метод наименьших квадратов

Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.

Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.

Параметры уравнений

Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.

Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.

Сгруппированные данные

Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.

Множественное парное уравнение регрессии: оценка важности связи

Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x₁,x₂,…,x_m)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.

Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.

Линейная функция изображается в форме такой взаимосвязи: у = а₀ + a₁х₁ + а₂х₂,+ . + a_mx_m. При этом _а2, a_m, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.

Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах₁ b1 х₂ b2 . x_m bm . В данном случае показатели b₁, b₂. b_m – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.

Какие факторы необходимо учитывать при построении множественной регрессии

Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.

Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:

• Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
• Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
• В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.

Методы построения

Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:

• Способ исключения.
• Способ включения.
• Пошаговый анализ регрессии.

Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.

Методы многомерного анализа

Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.