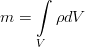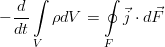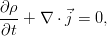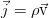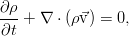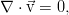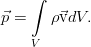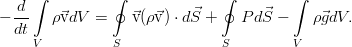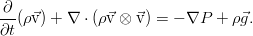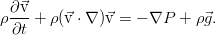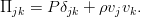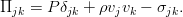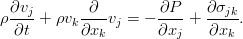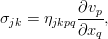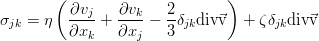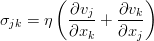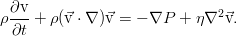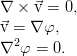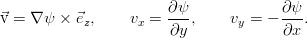Общие уравнения динамики жидкостей и газов

Общие законы и уравнения динамики жидкостей и газов

Уравнение Бернулли для потока идеальной жидкости выражает собой закон сохранения удельной энергии жидкости вдоль потока. Под удельной энергией понимают энергию, отнесенную к единице веса, объема или массы жидкости. Обычно удобнее бывает относить энергию к единице веса. В этом случае уравнение Бернулли, записанное для сечений 1 и 2 элементарной струйки или потока идеальной жидкости, имеет вид

(4.1)

где z – вертикальные координаты центров тяжести сечений или удельная энергия положения;

p/(ρg) –пьезометрическая высота, или удельная энергия давления;

υ 2 /(2g) – скоростная высота (напор), или удельная кинетическая энергия;

H – полный напор, или полная удельная энергия жидкости.

Рис.18. Графическая иллюстрация уравнения Бернулли для потока реальной жидкости

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

(4.2)

где υ_ср – средняя по сечению скорость, равная υ_cp= Q/А;

α – коэффициент Кориолиса, учитывающий неравномерность распре-деления скоростей по сечениям и равный отношению действительной ки-нетической энергии, потока к кинетической энергии того же потока, но при равномерном распределении скоростей;

Σh – суммарная потеря полного напора между сечениями 1 и 2.

С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ₁ω ₁ = υ₂ω₂.

Величина потерь напора (удельной энергии) определяется многими факторами: площадью поперечного сечения и длиной трубопровода, шероховатостью его внутренней поверхности, наличием местных сопротивлений, скоростью и режимом течения, вязкостью жидкости.

Различают два вида гидравлических потерь напора: местные потери и потери на трение по длине:

= h_лин + h_мест (4.3)

Рис.19 . Гидравлические потери по длине(а)и местные(б,в,г)

Местные потери напора происходят в так называемых местных гидравлических сопротивлениях, т. е. в местах изменения формы и размеров русла, где поток так или иначе деформируется — расширяется, сужается, искривляется — или имеет место более сложная деформация.

Где ζ_м – безразмерный коэффициент местного сопротивления.

Местные потери выражаются формулой Вейсбаха:

Потери напора по длине определяются общей формулой Дарси:

Для определения потерь давления используются формулы:

Два режима течения жидкости

Течение реальной жидкости характеризуется различными режимами ее движения, которые могут переходить один в другой при определенных условиях. Экспериментальные исследования гидравлических сопротивлений показывают, что потери напора (потери энергии) зависят от существующего в потоке режима движения.

Существование двух принципиально разных режимов движения жидкости было отмечено Г. Хагеном в 1839 и 1854 г г. В 1880 г. Д. И. Менделеев также высказал суждение о существовании двух режимов движения жидкости вследствие различия законов сопротивления движению. Позже английский физик О. Рейнольдс, а затем профессор Петербургского технологического института Н. П. Петров экспериментально подтвердили наличие двух режимов.

При изучении течения всевозможных капельных жидкостей с различными физическими свойствами. Рейнольдс установил, что движение бывает ламинарным и турбулентным.

«Ламинарный» происходит от латинского слова lamina — слой. Ламинарным называется такой режим, когда поток жидкости движется отдельными струйками или слоями и траектории отдельных частиц между собой не пересекаются. В практике ламинарный режим имеет место при движении жидкостей с большой вязкостью (нефти, смазочных масел), при движении воды через тонкие трубки, в трубопроводах при малых скоростях потока.

«Турбулентный» происходит от латинского слова turbulentus — беспорядочный. Турбулентным называется такой режим, когда струйность потока нарушается, все струйки перемешиваются и траектории движущихся частиц приобретают сложную форму, пересекаясь между собой.

В практике чаще всего имеет место турбулентный режим движения жидкости.

Установка Рейнольдса для исследования режимов движения жидкости пред ста влена на рис. 27. Сосуд А заполняется испытуемой жидкостью. К сосуду А в нижней его части присоединена стеклянная трубка 1 с краном 2, которым регулируется скорость течения в трубке. Над сосудом А расположен сосуд сраствором краски, от которого отходит трубка скраном . По мере открытия крана увеличивается скорость движения и режим движения переходит в турбулентный, при этом струйка приобретает волнообразный характер, а при еще большей скорости совсем размывается и смешивается с жидкостью в трубке. При постепенном закрытии крана эти явления протекают в обратном порядке, т. е. турбулентный режим сменяется ламинарным.

Опыты показали, что переход от турбулентного режима к ламинарному происходит при определенной скорости (эта скорость называется критической),которая различна для разных жидкостей и диаметров труб; при этом критическая скорость растет с увеличением вязкости жидкости и с уменьшением диаметра труб.

Рейнольдсом и рядом других ученых опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее основные характеристики потока

, (4.8)

где – скорость, м/сек; R — гидравлический радиус, м; v — кинематический коэффициент вязкости, м2/сек.

Это отношение называется числом Рейнолъдса. Значение числа Re, при котором турбулентный режим переходит в ламинарный, называют критическим числом Рейнолъдса ReKp.

Если фактическое значение числа Re, вычисленного по формуле (82), будет больше критического Re > ReKp – режим движения турбулентный, когда Re

ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры.

Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор.

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Кратко о гидродинамике: уравнения движения

Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.

В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.

Понятие сплошной среды

В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.

Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.

Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.

Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.

Уравнение неразрывности. Закон сохранения массы

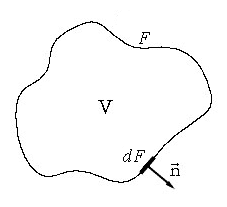
Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:

И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):

где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.

В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:

Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.

Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:

Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:

Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:

которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.

Уравнение Эйлера. Закон сохранения импульса

Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.

Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:

При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:

• конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
• давления окружающих элементов жидкости
• просто за счёт внешних сил, например — от силы тяжести.

Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:

Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:

Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.

В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:

Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.

Учёт вязкости. Уравнение Навье-Стокса

Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.

Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:

По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:

Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:

Оно допускает любой закон для вязкости.

Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:

в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:

где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости

носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:

Точные решения

Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.

Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.

Потенциальные течения

Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:

Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.

Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):

которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.

Простые течения вязкой жидкости

Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.

Сдвиговое течение Куэтта

Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.

В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:

Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.

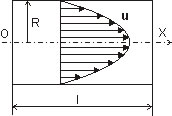
Течение Пуазейля

Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:

На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.

Стекание слоя жидкости по наклонной плоскости

Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.

В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.

Основы гидрогазодинамики и тепломоссообмена

«Основы гидрогазодинамики и тепломоссообмена»

Раздел 1. Гидрогазодинамика

Тема 1.2. Динамика жидкости и газа

Лекция 2. Анализ процессов движения жидкости будем проводить (если это не будет оговариваться особо) для идеальной жидкости, основным критерием идеальности для которой будет отсутствие вязкости. Такая подвижная жидкость будет обладать целым рядом свойств реальной неподвижной жидкости: в ней возможен лишь один вид напряжения – нормальное напряжение сжатия или то же самое, что и гидромеханическое давление.

Данное давление будет обладать в движущейся жидкости теми же свойствами, что и в реальной неподвижной: на внешней поверхности оно направлено по внутренней нормали, а в любой точке внутри жидкости – одинаково по всем направлениям.

Кроме этого, в основном будет рассматриваться стационарный режим течения, при котором давление и скорость являются функциями лишь координат и не зависят от времени, то есть

при этом

Дальнейшей степенью идеализации, принятой в механике жидкости, является понятие о струйчатой структуре потока жидкости, в соответствии с которым поток представляется как совокупность элементарных струек, прилегающих вплотную друг к другу и образующих сплошную массу движущейся жидкости. В связи с этим вначале вводят понятие линии тока – такой линии, касательные к каждой точке которой совпадают с направление вектора скорости в данной точке. При стационарном режиме течения жидкости линия тока совпадает с траекторией движения частицы жидкости.

Если внутри потока жидкости выделить бесконечно малый замкнутый контур и через каждую точку контура провести линию тока, то получим замкнутую поверхность, называемую трубкой тока. Часть потока жидкости, заключенная внутри трубки тока называется элементарной струйкой. Таким образом, элементарная струйка оказывается изолированной от остальной массы жидкости и является непроницаемой для жидкости, то есть ни одна части жидкости не может выйти наружу из трубки тока и ни одна частица не может проникнуть внутрь трубки тока из вне. Длина элементарной струйки не ограничена, а площадь ее поперечного сечения может меняться по длине, при этом в виду малости поперечного сечения элементарной струйки скорость во всех точках этого сечения можно считать одинаковой.

Скорость частицы жидкости может меняться по длине элементарной струйки или оставаться постоянной. В первом случае имеем неравномерное течение жидкости, во втором – равномерное. Для возможности сравнительного анализа равномерного и неравномерного течения жидкости введем понятие расхода жидкости.

Пусть в некотором поперечном сечении элементарной струйки площадью скорость жидкости равна . За элементарный отрезок времени частицы жидкости переместятся на расстояние . В силу сплошности жидкой среды, следующие за ними частицы жидкости заполнят все освободившее пространство. Таким образом, за указанный отрезок времени через поперечное сечение элементарной струйки пройдет объем жидкости, равный .

Объем жидкости, протекающий через поперечное сечение элементарной струйки в единицу времени, принято называть объемным расходом жидкости. Обычно его обозначают через . Тогда имеет

(1.33)

Исходя из условия сплошности среды, можно заключить, что объемные расходы в различных сечениях по длине элементарной струйки будут равны. Данное положение называется уравнением расхода для элементарной струйки и записывается в виде

=const (1.34)

Алгебраическая сумма расходов всех элементарных струек, составляющих данный поток, будет представлять собой объемный расход потока

(1.35)

Ранее было условлено, что в силу малости поперечного сечения элементарной струйки скорость жидкости во всех точках поперечного сечения одинакова. Но при этом скорость жидкости в различных элементарных струйках, составляющих поток, может быть различной. Для характеристики движения всего потока вводят в рассмотрение среднюю (одинаковую по всему сечению потока) скорость, которая определяется по выражению

(1.36)

В системах вентиляционных воздуховодов, в системах водоотведения часто применяют трубопроводы не круглого сечения. В этом случае при проведении гидравлических расчетов для характеристики размеров и формы поперечного сечения потока вводится понятие живого сечения, смоченного периметра и гидравлического радиуса.

Живым сечением потока (площадью живого сечения ) называется площадь сечения трубопровода, проведенная нормально к направлениям линий тока (нормально к направлениям скоростей элементарных струек) и заполненную жидкостью. Живое сечение может быть ограничено твердыми стенами трубопровода полностью или частично (в этом случае часть живого сечения ограничивается открытой поверхностью жидкости). Если стенки трубопровода ограничивают поток полностью, то движение жидкости в этом случае называют напорным. Если же ограничение частичное, то движение называют безнапорным. Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока в общем случае отлично от атмосферного и может быть как больше, так и меньше последнего. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному давлению. Примером напорного движения может служить движение жидкости при ее перекачке по трубопроводу за счет энергии, создаваемой насосом. Примером безнапорного движения может служить движение жидкости в открытых каналах, реках.

Часть периметра живого сечения, по которому поток жидкости соприкасается с ограничивающими его стенками, называют смоченным периметром — . Для круглого трубопровода в случае напорного движения смоченный периметр равен длине окружности; в случае безнапорного движения – длине дуги поверхности, по которой жидкость соприкасается со стенками трубопровода, так как свободная поверхность, по которой жидкость соприкасается с воздухом, в длину смоченного периметра на входит.

Отношение площади живого сечения к смоченному периметру называют гидравлическим радиусом сечения

(1.37)

Следует иметь в виду, что гидравлический радиус и геометрический радиус – разные понятия. Для примера, при напорном движении жидкости в круглом трубопроводе диаметром d геометрический радиус равен , а гидравлический — .

Кроме этих понятий в инженерной практике гидравлических расчетов используют понятие эквивалентного диаметра, который вычисляется по следующему выражению

(1.38)

Выше было введено понятие потока жидкости и газа. В гидрогазодинамике рассматривают три вида потоков: напорный, безнапорный и струи.

Напорный поток – это поток, при котором жидкость занимает все сечение трубопровода, а источником движения жидкости являются внешние источники энергии (например, насос).

Безнапорный поток – это поток с открытой в атмосферу внешней поверхностью и движущийся за счет сил гравитации.

Струи – это поток жидкости или газа со всех сторон окруженный жидкой или газообразной средой.

Аналогия напорным и безнапорным потокам жидкости существует и в газах.

Поток газа в трубопроводе, закрытом канале или воздуховоде запол­няет сечение полностью, соприкасаясь со стенками, поэтому он аналогичен напорному. Такие потоки, например, наблюдаются в системах вентиляции.

Аналогию с безнапорными потоками можно проследить в так назы­ваемых свободных струях. Например, в струях тёплого воздуха — воздуш­ных завесах, устраиваемых зимой при входе в общественные здания.

В аэродинамике для определения площади живого сечения w, м2, расхода потока Q, м3/с, скорости потока v, м/с, можно исполь­зовать зависимости из гидравлики, заменив слово – жидкость на – газ.

Например, для воздуховода прямоугольного сечения со сторонами a и b эквивалентный диаметр находится так:

dэ = 4w/ = 2ab/(a + b) .

Уравнение Бернулли для элементарной струйки идеальной жидкости

Уравнение Бернулли, помимо уравнения расхода, является основным уравнением гидродинамики, устанавливающим зависимость между скоростью и давлением в различных сечениях одной и той же элементарной струйки жидкости.

Выделим в потоке жидкости одну из элементарных струек и сечениями 1-1 и 2-2 ограничим в ней участок произвольной длины (рис.1 ) .

Для первого сечения зададим следующие параметры: площадь , скорость в сечении и давление , центр тяжести сечения расположен относительно произвольной плоскости сравнения на расстоянии . Для второго сечения соответственно имеем: . Под действием внешних сил за бесконечно малый промежуток времени выделенный участок переместится в положение .

Рисунок 1. К выводу уравнения Бернулли

Применим к выделенному участку элементарной струйки теорему механики о том, что работа внешних сил, приложенных к телу, равна приращению кинетической энергии этого тела, то есть . В нашем случае внешними силами будут силы давления, действующие по нормали к поверхности выделенного участка элементарной струйки, и массовые силы в виде силы тяжести, которые и производят указанную выше работу, то есть (1.39)

Работа сил давления складывается из работы в первом и втором сечениях, а так же работы на боковой поверхности элементарной струйки:

(1.40)

Работа сил давления в первом сечении на пути является положительной и определяется по выражению:

(1.41)

Работа сил давления во втором сечении (отрицательная) равна:

(1.42)

Силы давления, действующие на боковую поверхность работы не производят, поскольку они действуют по нормали к этой поверхности, а следовательно и по нормали к направлению перемещения жидкости. Таким образом

(1.43)

Работа массовых сил (силы тяжести) пропорциональна изменению потенциальной энергии положения выделенного участка элементарной струйки. Для нахождения этого изменения необходимо из потенциальной энергии положения жидкости в объеме 1-2 вычесть потенциальную энергию положения жидкости в объеме . Не трудно заметить, что при таком вычитании потенциальная энергия положения объема жидкости сократится. Поэтому в расчетах будет присутствовать лишь разность потенциальной энергии положения объемов и . Используя уравнение расхода, нетрудно заметить, что объемы, а, следовательно, и веса участков элементарной струйки и равны. Тогда можем записать

где – удельный вес жидкости

В таком случае работу сил тяжести можем записать как

(1.45)

Для определения приращения кинетической энергии выделенного участка элементарной струйки за тот же самый отрезок времени , следует из кинетической энергии объема вычесть кинетическую энергию объема : . Руководствуясь теми же соображениями, что и при подсчете потенциальной энергии, в результате получим

(1.46)

Подставляя выражения для работы сил давления, силы тяжести и приращения кинетической энергии в исходное уравнение, получим

(1.47) Разделив все члены уравнения (1.47) на , и делая соответствующие преобразования, в итоге получим

(1.48)

Группируя члены с одноименными индексами и учитывая, что сечения в элементарной струйке идеальной жидкости выбраны произвольно, имеем

(1.49)

Полученное уравнение (1.49) называется уравнением Бернулли; входящие в него члены имеют линейную размерность и в гидравлике имеют наименование:

— нивелирная высота или геометрический напор;

— пьезометрическая высота или пьезометрический напор;

— скоростная высота или скоростной (динамический) напор.

Соответственно трехчлен называют полным напором.

С геометрической точки зрения уравнение Бернулли говорит о том, что сумма трех напоров – геометрического, пьезометрического и скоростного есть величина постоянная вдоль элементарной струйки идеальной жидкости (рис.2).

Рисунок 2. Геометрическая интерпретация уравнения Бернулли

На рисунке можно выделить три характерные линии и области:

I–я область, расположенная между линией, соединяющей центры сечений идеальной струйки (линия геометрического напора) и линией сравнения, – зона геометрического напора.

II-я область, расположенная между линией геометрического напора и линией пьезометрического напора, – область изменения пьезометрического напора.

III-я зона, расположенная между пьезометрической линией и линией скоростного напора, – область изменения скоростного напора.

Полный напор Н в уравнении Бернулли можно рассматривать как полную удельную энергию (то есть энергию, отнесенную к единице веса) жидкости в данном сечении элементарной струйки.

Тогда входящие в него члены являются удельной энергией положения, удельной энергией давления и удельной кинетической энергией.

В соответствии с этим с энергетической точки зрения уравнение Бернулли можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, то есть сумма удельной энергии положения, удельной энергии давления и удельной кинетической энергии, есть величина постоянная во всех сечениях по длине струйки.

Приведённое полное давление

В любой точке движущегося газа действует полное давление

где pст — статическое давление ;

pд = rv2/2—динамическое давление, отражающее кинети­ческую энергию потока газа.

Однако величина полного давления pп не охватывает полную энергию точки движущегося газа, так как в ней не содержится давление по­ложе­ния точки rgz. Поэтому в качестве энергетической характери­сти­ки любой точки потока газа введём понятие приведённого полного давления (рис. 26):

Первые два члена rgz + pст представляют собой потенциальную часть энер­гии, а последний rv2/2 — кинетическую.

Уравнение Бернулли для газа

Рассмотрим поток газа, проходящий по трубопроводу переменно­го се­че­ния (рис. 27). В первом сечении приведённое полное давление ра­вно pпр. п1. При прохождении по трубе часть pпр. п1 необратимо потеря­ется из-за проявле­ния сил внутреннего трения газа и во втором сечении энергетиче­ская хара­к­теристика уменьшится до pпр. п2 на величину потерь давле­ния Dpпот.

Уравнение Бeрнулли для газа в простейшем виде записы­вается так:

то есть это уравнение для двух сечений потока в направлении его движения, выраженное через приведённые полные давления и отражающее закон со­хра­нения энергии (часть энергии переходит в потери) при движении газа.

Уравнение Бeрнулли в традиционной записи получим, если в по­следнем ра­венстве раскроем значения приведённых полных давлений pпр. п1 и pпр. п2:

.

Энергетический смысл уравнения Бeрнулли для газа заключается в том, что оно отражает закон сохранения энергии, а геометрический не рассматривается, так как величины в нём выражаются в единицах дав­ления (Па), а не на­пора (м).

Разность давлений и потери давления

Особенности терминов «разность давлений» и «поте­ри давле­ния» поясним на примерах.

Движение газа происходит только при наличии разности приве­дённых полных давлений

pпр = pпр. п1 — pпр. п2

от точки с большим давлением pпр. п1 к точке с ме­ньшим pпр. п2. Например, это является условием работы систем естественной вентиляции зданий: для удаления воз­духа из помещения давление pпр. п внутри должно быть боль­ше, чем снару­жи.

Потери давленияpпот отражают потерю полной энергии потока при движении газа. Например, чем длиннее воздуховод, меньше его про­ходное сечение, шероховатее его стенки, тем больше будут потери давления в системе вентиляции, что может ухудшить удаление несвежего воздуха из помещений. В покоящемся газе никаких потерь давле­ния нет.

При установившемся движении газа разность давлений равна потерям давления:

pпр = pпот,

что является уравнением Бернулли в простейшей записи.

Таким образом, «разность давлений» является причиной движения газа, а «потери давления»- следствием. При движении газа они чис­ленно равны. Измеряются они в одних и тех же единицах СИ: паскалях (Па).

Два режима движения жидкости (газа).

Исследование вопроса о механизме движения жидкости (газа) показывает, что в природе существуют два вида (режима) движения жидкости: во-первых, слоистое, упорядоченное или ламинарное движение, при котором отдельные слои жидкости скользят друг относительно друга, не смешиваясь между собой, и, во-вторых, неупорядоченное или турбулентное движение, при котором частицы жидкости движутся по сложным, постоянно меняющимся траекториям и в потоке происходит интенсивное перемешивание микро — и макромасс жидкости. Основной особенностью турбулентного режима течения является наличие поперечных к основному направлению движения составляющих скоростей, накладывающихся на основную скорость в продольном направлении.

Выяснению условий существования ламинарного или турбулентного режима течения жидкости, влияния физических характеристик жидкости на переход из одного режима в другой были посвящены опыты Рейнольдса.

Рейнольдс установил, что основными факторами, определяющими характер режима, являются: средняя скорость движения жидкости , диаметр трубопровода , плотность жидкости , абсолютная вязкость , а переход от ламинарного режима к турбулентному происходит при определенной скорости – критической скорости, различной для труб разных диаметров и возрастающей с увеличением вязкости жидкости и уменьшающейся с уменьшением диаметра трубы.

Для характеристики режима движения жидкости Рейнольдсом был выведен безразмерный параметр , учитывающий влияние перечисленных выше факторов и называемый числом (критерием) Рейнольдса

(1.53)

Так как отношение где — коэффициент кинематической вязкости жидкости (газа), то выражение (1.52) можно записать в виде

(1.54)

Границы существования того или иного режима движения жидкости определяются двумя критическими значениями числа Рейнольдса: нижним критическим числом и верхним критическим числом . При значениях чисел Рейнольдса возможен только ламинарный режим, а при — только турбулентный режим; при наблюдается неустойчивое состояние потока. Таким образом, для определения режима течения необходимо в каждом случае вычислять по выражению (1.53 или 1.54) число Рейнольдса и сопоставлять его с критическим значением.

В опытах самого Рейнольдса значение были следующие: . Последующие эксперименты показали, что критические числа Рейнольдса не являются вполне постоянной величиной и что при определенных условиях неустойчивая зона может быть значительно шире. В настоящее время при практических расчетах принято исходить из одного значения критического числа Рейнольдса, равного , считая, что при всегда имеет место ламинарный режим, а при – всегда турбулентный. При этом движение в неустойчивой зоне исключается из рассмотрения, что приводит к некоторому запасу и большей надежности при гидравлических расчетах в том случае, если в этой зоне в действительности имеет место ламинарный режим течения.

Проведенные исследования особенностей различных режимов движения жидкости показывают, что одновременно с переходом от ламинарного режима к турбулентному изменяется характер распределения скоростей по поперечному сечению потока, а также зависимость потерь энергии (напора). Установлено, что для ламинарного режима характерен параболический закон распределения скоростей по поперечному сечению: скорость жидкости равна нулю непосредственно у стенок трубопровода, а при удалении от них плавно и непрерывно возрастает, достигая максимума на оси трубопровода (рис.3а).

Рисунок 3. Характер распределения скоростей по перечному сечению потока при ламинарном (а) и турбулентном (б) режиме движения.

Турбулентному режиму движения присущ более сложный закон распределения скоростей по поперечному сечению: в пределах большей части поперечного сечения скорость весьма незначительно отличается от максимального значения на оси трубопровода, но при этом начинает резко падать вблизи стенок трубопровода (рис.3б).

Причиной такого более равномерного закона распределения скоростей при турбулентном режиме является наличие поперечных составляющих скоростей частиц жидкости. В результате этого частицы жидкости с большими скоростями на оси потока и с меньшими скоростями на удалении от оси непрерывно сталкиваются, что приводит к выравниванию их скоростей. В тоже время вблизи стенок трубопровода такое взаимное перемещение частиц друг относительно другу нейтрализуется наличием твердой границы (стенки трубопровода), что и обуславливает более интенсивное падение скорости жидкости.

Если обеспечить протекание жидкости по трубопроводу с различной скоростью и замерить при этом величину потерь напора, то графическая зависимость будет иметь следующий вид (рис.4).

Рисунок 4. Зависимость потерь напора от скорости потока

В некотором диапазоне скоростей (зона I) потери напора изменяются пропорционально скорости, а затем, при достижении определенного значения скорости, потери напора становятся пропорциональны более высокой степени скорости (зона II). Этот переход от одного закона к другому происходит при значении скорости, равного критическому, то есть в момент перехода от ламинарного режима к турбулентному.

Следовательно, при ламинарном режиме потери напора пропорциональны первой степени скорости, а при турбулентном – степени больше единицы .

Таким образом, ламинарный и турбулентный режимы отличаются не только характером движения частиц (отдельных масс) жидкости в потоке, но и разными законами распределения скоростей по поперечному сечению и разными законами, определяющими зависимость между потерями напора и скоростью жидкости в потоке.

На практике в большинстве случаев (движение жидкости по трубопроводам, каналах и пр.) приходится иметь дело с турбулентным режимом. Ламинарный режим, который встречается гораздо реже, наблюдается при движении очень вязких жидкостей, при движении жидкости по очень узким каналам (фильтрование), в порах естественных грунтов.

Пример 1. Определить режим движения жидкости в лотке пря­моугольной формы высотой 0,2 м и шириной 0,5 м при уровне воды 0,15 м и скорости = 1,2 м/c (рис. 5).

Решение: Принимая =0,0110-4 м2/с (для воды), опре­де­ляем:

.

Так как Re > Reкр = 2300, то режим движения потока будет тур­булентным.

ОЦЕНОЧНЫЕ СРЕДСТВА раздела 1 темы 1.2

Давление в движущейся идеальной жидкости обладает свойствами:

А. Не обладает ни какими свойствами

Б. Теми же свойствами, что и в покоящейся реальной жидкости

В. В идеальной жидкости давление отсутствует.

Г. Давление всегда идеальное

А. Линия, соединяющая два проводника, по которым протекает разный по величине электрический ток

Б. Линия в движущейся жидкости, касательные к которой в любой ее точке совпадают с направлением вектора скорости частицы, расположенной на этой линии в данный момент времени

В. Линия, по которой в данный момент времени протекает наибольший электрический ток

Г. Вообще любая линия электропередачи

Трубка тока это:

А. Трубчатая поверхность, образованная путем проведения линий тока через каждую точку замкнутого контура, расположенного в движущейся жидкости

Б. Трубчатый проводник, по которому протекает электрический ток

В. Трубчатая поверхности, через боковую поверхность протекает жидкость

Живое сечение потока это:

А. Сечение, которое живее всех живых

Б. Сечение, которое проявляет признаки жизни в данный момент времени

В. Часть поперечного сечения канала (трубопровода), заполненного жидкостью

В. Сечение, через которое протекает «живая вода»

Уравнение расхода определяет:

А. Как наилучшим образом расходовать имеющуюся наличность

Б. Постоянство расхода жидкости по длине трубопровода

В. Изменение расхода жидкости по длине трубопровода

Смоченный периметр это:

А. Периметр любой геометрической фигуры на чертеже, опущенной в воду

Б. Периметр любой геометрической фигуры, который является самым мокрым среди других

В. Часть периметра живого сечения, по которой жидкость соприкасается со стенками канала

Гидравлический радиус это:

А. Величина, которой в гидравлике измеряют давление

Б. Понятие, не имеющее смысла

В. Радиус окружности, очерченной гидравлическим циркулем

Г. Отношение площади живого сечения к смоченному периметру

Уравнение Бернулли для идеальной жидкости записывается следующим образом:

А.

В.

Г.

Энергетический смысл уравнения Бернулли для идеальной жидкости:

А. Полная удельная энергия вдоль элементарной струйки идеально жидкости убывает

Б. Полная удельная энергия вдоль элементарной струйки идеально жидкости постоянна

В. Полная удельная энергия вдоль элементарной струйки идеально жидкости возрастает

При выводе уравнения Бернулли для потока реальной жидкости допускается, что

А. Гидростатическое давление равно нулю

Б. Гидростатическое давление одинаково по всему поперечному сечению потока

В. В пределах поперечного сечения потока справедлив основной закон гидростатики

Скоростной напор в уравнении Бернулли для потока реальной жидкости выражается через:

А. Среднюю скорость потока

Б. Через первую космическую скорость

В. Значение скорости в нем отсутствует

Г. Через максимальную скорость на оси потока

Условие существования ламинарного режима

А. Re2300

Б. Re2300

Условие существования турбулентного режима

А. Re2300

Б. Re2300

Для какого режима течения распределение скоростей по поперечному сечению более равномерное

А. Для ламинарного

Б. Для турбулентного

В. Одинаково для обоих режимов

1. Для проверки умений определять гидравлические характеристики потока найдите гидравлический радиус для трех трубопроводов следующих форм поперечного сечения: 1. квадратное со стороной «а», 2. прямоугольное со сторонами «ав», 3. равносторонний треугольник со стороной «а».

2. Продемонстрируйте умения применять знания темы 1.1, 1.2 на примере решения следующих задач:

а). Жидкость плотностью 900 кг/м3 и кинематической вязкостью =3,3м2/с перекачивается на расстояние 1,5 км по горизонтальной трубе диаметром 0,075 м. Массовый расход G=кг/час. Доказать, режим течения является ламинарным.

Доказательство проводится путем сравнения расчетного значение числа Re c критическим значением.

б). Жидкость ( кг/м3, = Пас) течет по вертикальной трубе диаметром 3 см. Давление на высоте Z1=100 мм составляет 250кПа. Определить направление движения, если давление на высоте Z2=85 мм равно 250 к Па. Какова скорость течения жидкости на оси трубы и на расстоянии 6 мм от ее оси, если режим движения ламинарный?