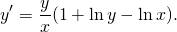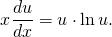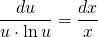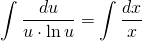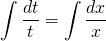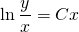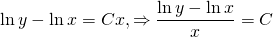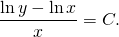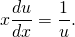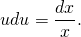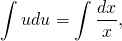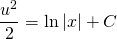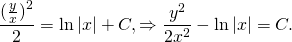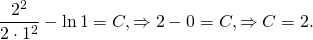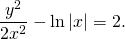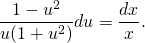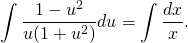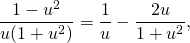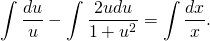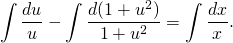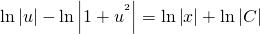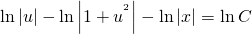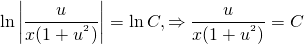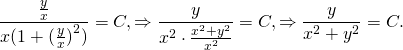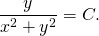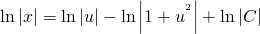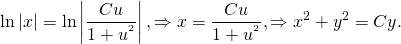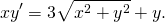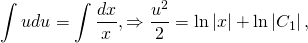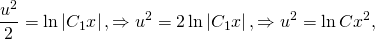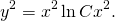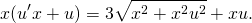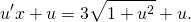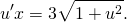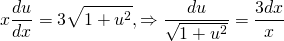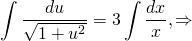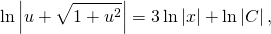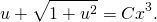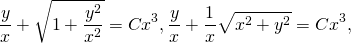Общий интеграл однородного дифференциального уравнения первого порядка

Однородные дифференциальные уравнения первого порядка

Определение

Как определить однородное дифференциальное уравнение

Для того, чтобы определить, является ли дифференциальное уравнение первого порядка однородным, нужно ввести постоянную t и заменить y на ty и x на tx : y → ty , x → tx . Если t сократится, то это однородное дифференциальное уравнение. Производная y′ при таком преобразовании не меняется.
.

Пример

Определить, является ли данное уравнение однородным

Делаем замену y → ty , x → tx .

Делим на t 2 .

.
Уравнение не содержит t . Следовательно, это однородное уравнение.

Метод решения однородного дифференциального уравнения

Однородное дифференциальное уравнение первого порядка приводится к уравнению с разделяющимися переменными с помощью подстановки y = ux . Покажем это. Рассмотрим уравнение:
(i)
Делаем подстановку:
y = ux ,
где u — функция от x . Дифференцируем по x :
y′ = ( ux ) ′ = u′ x + u ( x ) ′ = u′ x + u
Подставляем в исходное уравнение (i).
,
,
(ii) .
Разделяем переменные. Умножаем на dx и делим на x ( f ( u ) – u ) .

При f ( u ) – u ≠ 0 и x ≠ 0 получаем:

Интегрируем:

Таким образом, мы получили общий интеграл уравнения (i) в квадратурах:

Заменим постоянную интегрирования C на ln C , тогда

Опустим знак модуля, поскольку нужный знак определяется выбором знака постоянной C . Тогда общий интеграл примет вид:

Далее следует рассмотреть случай f ( u ) – u = 0 .
Если это уравнение имеет корни, то они являются решением уравнения (ii). Поскольку уравнение (ii) не совпадает с исходным уравнением, то следует убедиться, что дополнительные решения удовлетворяют исходному уравнению (i).

Всякий раз, когда мы, в процессе преобразований, делим какое-либо уравнение на некоторую функцию, которую обозначим как g ( x, y ) , то дальнейшие преобразования справедливы при g ( x, y ) ≠ 0 . Поэтому следует отдельно рассматривать случай g ( x, y ) = 0 .

Пример решения однородного дифференциального уравнения первого порядка

Проверим, является ли данное уравнение однородным. Делаем замену y → ty , x → tx . При этом y′ → y′ .
,
,
.
Сокращаем на t .

Постоянная t сократилась. Поэтому уравнение является однородным.

Делаем подстановку y = ux , где u – функция от x .
y′ = ( ux ) ′ = u′ x + u ( x ) ′ = u′ x + u
Подставляем в исходное уравнение.
,
,
,
.
При x ≥ 0 , |x| = x . При x ≤ 0 , |x| = – x . Мы пишем |x| = ± x подразумевая, что верхний знак относится к значениям x ≥ 0 , а нижний – к значениям x ≤ 0 .
,
Умножаем на ± dx и делим на .

При u 2 – 1 ≠ 0 имеем:

Интегрируем:

Интегралы табличные,
.

Применим формулу:
( a + b )( a – b ) = a 2 – b 2 .
Положим a = u , .
.
Возьмем обе части по модулю и логарифмируем,
.
Отсюда
.

Таким образом имеем:
,
.
Опускаем знак модуля, поскольку нужный знак обеспечивается выбором знака постоянной C .

Умножаем на x и подставляем ux = y .
,
.
Возводим в квадрат.
,
,
.

Теперь рассмотрим случай, u 2 – 1 = 0 .
Корни этого уравнения
.
Легко убедиться, что функции y = ± x удовлетворяют исходному уравнению.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 19-07-2012 Изменено: 24-02-2015

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Как решить однородное дифференциальное уравнение

Чтобы решить однородное дифференциальное уравнение 1-го порядка, используют подстановку u=y/x, то есть u — новая неизвестная функция, зависящая от икса. Отсюда y=ux. Производную y’ находим с помощью правила дифференцирования произведения: y’=(ux)’=u’x+x’u=u’x+u (так как x’=1). Для другой формы записи: dy=udx+xdu.После подстановки уравнение упрощаем и приходим к уравнению с разделяющимися переменными.

Примеры решения однородных дифференциальных уравнений 1-го порядка.

1) Решить уравнение

Проверяем, что это уравнение является однородным (см. Как определить однородное уравнение). Убедившись, делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем: u’x+u=u(1+ln(ux)-lnx). Так как логарифм произведения равен сумме логарифмов, ln(ux)=lnu+lnx. Отсюда

u’x+u=u(1+lnu+lnx-lnx). После приведения подобных слагаемых: u’x+u=u(1+lnu). Теперь раскрываем скобки

u’x+u=u+u·lnu. В обеих частях стоит u, отсюда u’x=u·lnu. Поскольку u — функция от икса, u’=du/dx. Подставляем,

Получили уравнение с разделяющимися переменными. Разделяем переменные, для чего обе части умножаем на dx и делим на x·u·lnu, при условии, что произведение x·u·lnu≠0

В левой части — табличный интеграл. В правой — делаем замену t=lnu, откуда dt=(lnu)’du=du/u

ln│t│=ln│x│+C. Но мы уже обсуждали, что в таких уравнениях вместо С удобнее взять ln│C│. Тогда

ln│t│=ln│x│+ln│C│. По свойству логарифмов: ln│t│=ln│Сx│. Отсюда t=Cx. ( по условию, x>0). Пора делать обратную замену: lnu=Cx. И еще одна обратная замена:

По свойству логарифмов:

Это — общий интеграл уравнения.

Вспоминаем условие произведение x·u·lnu≠0 (а значит, x≠0,u≠0, lnu≠0, откуда u≠1). Но x≠0 из условия, остается u≠1, откуда x≠y. Очевидно, что y=x ( x>0) входят в общее решение.

2) Найти частный интеграл уравнения y’=x/y+y/x, удовлетворяющий начальным условиям y(1)=2.

Сначала проверяем, что это уравнение является однородным (хотя наличие слагаемых y/x и x/y уже косвенно указывает на это). Затем делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем полученные выражения в уравнение:

u’x=1/u. Так как u — функция от икса, u’=du/dx:

Получили уравнение с разделяющимися переменными. Чтобы разделить переменные, умножаем обе части на dx и u и делим на x (x≠0 по условию, отсюда u≠0 тоже, значит, потери решений при этом не происходит).

и поскольку в обеих частях стоят табличные интегралы, сразу же получаем

Выполняем обратную замену:

Это — общий интеграл уравнения. Используем начальное условие y(1)=2, то есть подставляем в полученное решение y=2, x=1:

3) Найти общий интеграл однородного уравнения:

(x²-y²)dy-2xydx=0.

Замена u=y/x, откуда y=ux, dy=xdu+udx. Подставляем:

(x²-(ux)²)(xdu+udx)-2ux²dx=0. Выносим x² за скобки и делим на него обе части (при условии x≠0):

(1-u²)(xdu+udx)-2udx=0. Раскрываем скобки и упрощаем:

xdu-u²xdu-u³dx-udx=0. Группируем слагаемые с du и dx:

(x-u²x)du-(u³+u)dx=0. Выносим общие множители за скобки:

x(1-u²)du-u(u²+1)dx=0. Разделяем переменные:

x(1-u²)du=u(u²+1)dx. Для этого обе части уравнения делим на xu(u²+1)≠0 (соответственно, добавляем требования x≠0 (уже отметили), u≠0):

В правой части уравнения — табличный интеграл, рациональную дробь в левой части раскладываем на простые множители:

(или во втором интеграле можно было вместо подведения под знак дифференциала сделать замену t=1+u², dt=2udu — кому какой способ больше нравится). Получаем: