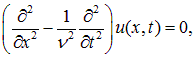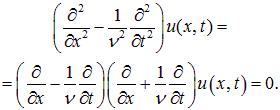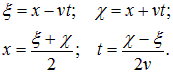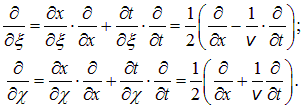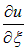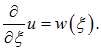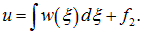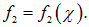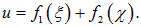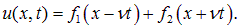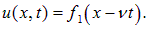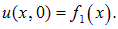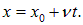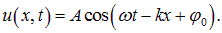Общий вид решения волнового уравнения

Волновое уравнение движущейся волны

Физика > Математическое отображение движущейся волны

Волновое уравнение – математическая формула движения волны. Рассмотрите, как вывести решение волнового уравнения, вид уравнения, граничные условия, примеры.

Наиболее общее волновое уравнение задается как u(x, t) = f (x + ct) + g (x — ct), где f и g – произвольные функции.

Задача обучения

• Вывести решение для волнового уравнения перемежающейся волны.

Основные пункты

• Любая функция u(x, t), подходящая к условию , выступает решением волнового уравнения. Для этого были введены новые переменные φ = x — ct, ψ = x + ct.
• Решения 1D-волнового уравнения – суммы левой и правой движущихся функций.
• Волновая функция также вычисляется путем получения дополнительной информации, обычно заданной граничными условиями.

Термины

• Волновое уравнение – линейной уравнение частных производных второго порядка для описания различных типов волн.
• Граничное условие – набор ограничений на границах, используемых в дифференциальных уравнениях.

Чаще всего, для одномерных волн используют уравнение:

Например, синусоидальная форма u(x, t) = A sin(kx — ωt) выступает решением волнового уравнения для с = ω/k.

Решение волнового уравнения

Отметим, что любая функция u(x, t), подходящая к условию , выступает решением волнового уравнения. Так что обратите внимание на

В середине мы использовали первое уравнение. Теперь вставим новые переменные φ = x — ct, ψ = x + ct и получим:

При смене переменных ∂u+/∂φ = 0 для уравнения со знаком «+» и ∂u-/∂ψ = 0 для знака «-». Поэтому мы видим, что

u₊(φ,ψ) = f(ψ), u_— (φ, ψ) = g(φ), где f и g – произвольные функции. Возвращаясь к исходным переменным x и t, выводим, что решение волнового уравнения:

u (х, t) = f (х + ct) + g (х — ct).

Мы видим, что решение для 1D-волнового уравнения отображает сумму левой (f) и правой (g) перемещающихся волн. Движение означает, что форма их отдельных произвольных функции по х остается стабильной, а вот время и скорость – нет.

Граничное условие

Любая функция с «x + ct» или «x — ct» может выступать решением волнового уравнения. Также можно вычислить при помощи дополнительной информации в виде граничного условия. Например, если речь идет о гитарной струне, то мы знаем, что волна обладает нулевой амплитудой на обоих концах: u (x = 0) = u (x = L) = 0.

Решение волнового уравнения в двух измерения с граничным условием нулевого смещения вдоль всего внешнего края.

Общий вид решения волнового уравнения

Волновое уравнение
_{Wave equation}

Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением

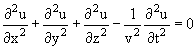(1)

где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид

u(x,t) = Asin(ωt − xv).

Длина волны λ − путь, пройденный возмущением (состоянием с определённой фазой) за время равное периоду колебаний T

Частота ω и период колебаний T связаны соотношением

Эквивалентные формулы для монохроматической волны, распространяющейся вдоль оси x

u(x,t) = Asin(ωt − kx) = Asinω(t − x/v) = Asin2π(t/T − x/λ).

u(r,t) = (A/r)sin(ωt − kr).

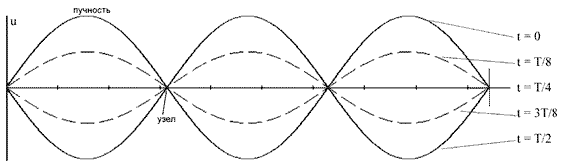
Стоячая волна. При наложении монохроматических волн одинаковой частоты образуется устойчивая картина результирующих колебаний с характерными максимумами и минимумами.

Стоячая волна образуется в системах с двумя жёстко закреплёнными точками. При отражении фаза волны меняется на π и происходит интерференция падающей и отраженной волн.

Соотношение (2) можно получить, используя формулу

sinα − sinβ = 2sin[(α − β)/2] cos[(α + β)/2]

и положив 2Asin(2πx/λ) = A(x), A(x) − амплитуда стоячей волны.

2.2. Решение волнового уравнения

Уравнение типа (2.2), описывающее колебания различных упругих сред, называется волновым уравнением. Запишем его формально в виде:

Введем теперь вместо (x, t) новые переменные:

Производные по новым переменным выражаются по стандартным правилам дифференцирования сложной функции:

Отсюда следует, что уравнение (2.16) в новых переменных записывается в виде:

Поскольку производная по 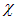равна нулю,

не зависит от этой переменной и, следовательно, является некоторой функцией w только от переменной :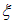

Интегрируем теперь это уравнение:

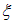
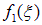
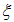
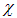
Первое слагаемое в правой части является только функцией переменной , которую мы обозначим как . Второе слагаемое — постоянная интегрирования. Она не зависит от , являясь, стало быть, функцией только переменной :

Мы получили, что решение волнового уравнения имеет вид:

Подставляя сюда выражения (2.17), мы возвращаемся к прежним переменным (x, t):

Функции f₁ и f₂ — совершенно произвольны и должны быть определены из начальных и граничных условий.

Обсудим физический смысл полученных решений. Ограничимся сначала первым слагаемым. Пусть

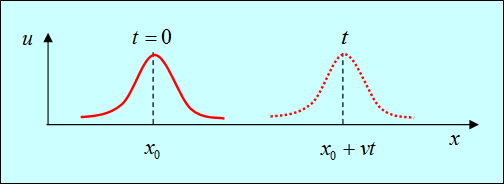
В момент времени t = 0 функция f₁(x) задает распределение смещений (профиль струны, деформацию твердого тела, распределение давления или частиц в газе и т. д.):

Предположим, например, что это распределение имеет максимум в точке 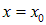(рис. 2.6).

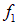
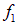
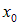
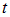
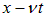
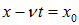
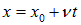
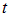
Такое распределение называют обычно волновым пакетом. В момент t максимум функции по-прежнему будет в точке, в которой аргумент равен , но теперь (в момент времени ) аргумент равен , таким образом: или . Другими словами, за время от 0 до волновой пакет сдвинется вправо на расстояние vt, так что максимум теперь придется на точку

Нетрудно сообразить, что форму свою волновой пакет при этом перемещении не изменит.

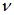
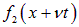
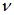
Мы видим, что начальное распределение движется вправо со скоростью . Аналогично, второе слагаемое, , описывает движение волнового пакета налево с той же скоростью . Общее решение (2.21) является суперпозицией двух этих решений.

В свою очередь, любой волновой пакет может быть представлен как суперпозиция гармонических функций. Отсюда — особая роль решений волнового уравнения вида:

Это решение описывает монохроматическую волну, распространяющуюся направо со скоростью