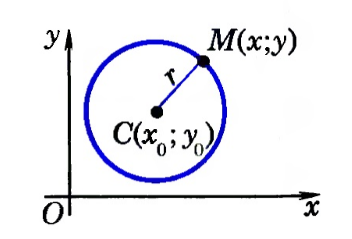Общий вид уравнений окружности и прямой

Общий вид уравнения окружности и прямой

Уравнение окружности и прямой

Вы будете перенаправлены на Автор24

Уравнение линии на плоскости

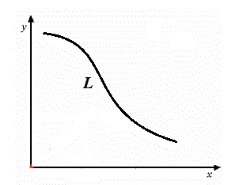
Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).

Рисунок 1. Произвольная линия в системе координат

Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$

Уравнение окружности

Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).

Рисунок 2. Окружность в декартовой системе координат

Расстояние от центра окружности до точки $M$ вычисляется следующим образом

Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее

Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.

В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид

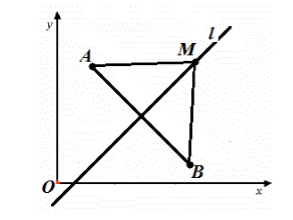
Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $\left\ $ и $\ $ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ — серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=\ $, принадлежащую прямой $l$ (рис. 3).

Готовые работы на аналогичную тему

Рисунок 3. Прямая в декартовой системе координат

Так как прямая $l$ — серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.

Найдем длины данных сторон по формуле расстояния между точками:

Обозначим через $a=2\left(x_1-x_2\right),\ b=2\left(y_1-y_2\right),\ c= ^2+ ^2- ^2- ^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:

Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=\ $, тогда

Если прямая $l$ параллельна оси $Ox$, то она имеет вид

Если прямая $l$ параллельна оси $Oy$, то она имеет вид

Пример задачи на нахождение уравнений линий в декартовой системе координат

Найти уравнение окружности с центром в точке $(2,\ 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.

Решение.

Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2,\ 4)$, получим

Найдем радиус окружности как расстояние от точки $(2,\ 4)$ до точки $(0,0)$

Получаем, уравнение окружности имеет вид:

Найдем теперь уравнение окружности, используя частный случай 1. Получим

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 05 04 2022

Геометрия. 9 класс

Конспект
Введём уравнение произвольной линии.
В прямоугольной системе координат рассмотрим произвольную линию L.

Уравнение с двумя переменными х и у называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Рассмотрим точки М и N в координатной плоскости.
y = f (x) – уравнение линии L, если выполняются условия:
М (х₁; у₁) ∈ L → y₁ = f (x₁)
N (х₂; у₂) ∉ L → y₂ ≠ f (x₂)
Теперь, зная метод координат и геометрические свойства окружности, выведем её уравнение.
Пусть в прямоугольной системе координат дана окружность, где C – центр окружности с координатами x₀ и y₀, а r – её радиус.
Расстояние от произвольной точки М с координатами х и у до точки С вычисляется по формуле:
Точка М лежит на окружности, то есть координаты точки М удовлетворяют этому уравнению. Значит, МС = r, MC₂ = r₂.
В прямоугольной системе координат уравнение окружности радиуса r и с центром (x — x₀) 2 + (y — y₀) 2 = r 2 имеет вид:
Если центр окружности находится в начале координат, то уравнение окружности с центром в начале координат будет выглядеть так:
Теперь выведем уравнение прямой. Снова рассмотрим прямоугольную систему координат.
Докажем, что любая прямая в декартовых координатах имеет уравнение ax + by + c = 0, где а, b, с – некоторые числа, а х и у – переменные координаты точки А, принадлежащей прямой.
Как и при составлении уравнения окружности, обратимся к свойству прямой, равноудаленной от двух данных точек. Пусть h – произвольная прямая на плоскости и точка А с координатами х и у – точка этой прямой. Точки В и С равноудалены от прямой h, точка D – это точка пересечения ВС с прямой h. Поэтому h – срединный перпендикуляр к отрезку ВС. Так как АС = АВ, то AС₂ = АB₂, значит координаты точки А удовлетворяют уравнению (х – хв)² + (у – ув)² = (х – хс)² + (у – ус)², где В (хв; ув) и С (хс; ус)
Следовательно, это уравнение и является уравнением прямой h в прямоугольной системе координат.
После алгебраических преобразований получаем уравнение прямой: ах + bу + с = 0, где a, b, c некоторые числа. Так как В и С различные точки, значит разность их координат не равна нулю.
Таким образом, уравнение прямой в прямоугольной системе координат является уравнением первой степени.

НАШИ ПАРТНЁРЫ

© Государственная образовательная платформа «Российская электронная школа»

Уравнение окружности и прямой

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

ТЕМА: «Уравнение окружности и прямой» Цели урока: Повторить уравнение окружности и прямой. Показать применение уравнений окружности и прямой при решении задач. Совершенствование навыков решения задач методом координат.

1. Как называется геометрическая фигура, состоящая из множества всех точек, равноудаленных от данной точки? Математический диктант Проверить 1. Окружность

2. Как называется хорда, проходящая через центр окружности? Проверить 2. Диаметр

3. Как называется отрезок, соединяющий центр окружности с точкой на окружности? Проверить 3. Радиус

4. Как называется геометрическая фигура, состоящая из множества всех точек плоскости, находящихся от данной точки на расстоянии, не превышающем данного? Проверить 4. Круг

5. Пересекаются ли окружности с центрами А и В, если АВ = 10 см, а радиусы равны 5 см, и 6 см? Проверить 5. Пересекаются

6. Расстояние от центра окружности до точки А равно d, а радиус окружности равен r. Сравните d и r, если точка А лежит вне круга, ограниченного данной окружностью? Проверить 6. d > r

7. Расстояние от центра окружности до точки В равно m, а радиус окружности равен r. Сравните m и r, если точка B лежит внутри круга, ограниченного данной окружностью? Проверить 7. m (0 – 1)2 + (0 + 3)2 = 9 > (0 – 1)2 + (1 + 3)2 = 9 > x

Дана окружность Определите, какие из точек А(-4; 3), В(5; 1), С(-5; 4), D(10; 5) лежат: а) на окружности; б) внутри круга, ограниченного данной окружностью; в) вне круга, ограниченного данной окружностью. (x – 4 )2 + (y + 3)2 = 100 (– 4 – 4)2 + (3 + 3)2 > 100 (5 – 4)2 + (1 + 3)2 100 (10 – 4)2 + (5 + 3)2 = 100

Найдите множество точек, удаленных от окружности на расстояние 3. x 2 + y 2 = 16 x y x 2 + y 2 = 49 x 2 + y 2 = 1

(x + 5)2 + (y – 5)2 = 25 Центр? Радиус? O1(-5;5) r = 5 x y A O O1 450 5 5

Центр? Радиус? x y O1 O E 300 На чертеже расстояние ОО1= , ОЕ – касательная к окружности. EOF = 600. Написать уравнение окружности. ОЕ = ОF, отрезки касательных 6

Домашнее задание п. 93 — 95 № 972(б), 973, 978 (а)

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 325 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 698 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 482 823 материала в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

§ 3. Уравнения окружности и прямой

Дистанционные курсы для педагогов

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 07.12.2020 935 —> —> —> —>
• PPTX 3 мбайт —> —>
• Оцените материал:

Настоящий материал опубликован пользователем Малышок Елена Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 8 лет и 1 месяц
• Подписчики: 1
• Всего просмотров: 33273
• Всего материалов: 28

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Китае приняли закон о сокращении нагрузки на школьников

Время чтения: 1 минута

Крупнейшие вузы Татарстана откроют цифровые кафедры в 2022 году

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Первый мониторинг вузов РФ по новым показателям пройдёт в 2023 году

Время чтения: 2 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Уравнение окружности и прямой

Вы будете перенаправлены на Автор24

Уравнение линии на плоскости

Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).

Рисунок 1. Произвольная линия в системе координат

Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$

Уравнение окружности

Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).

Рисунок 2. Окружность в декартовой системе координат

Расстояние от центра окружности до точки $M$ вычисляется следующим образом

Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее

Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.

В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид

Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $\left\$ и $\$ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ — серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=\$, принадлежащую прямой $l$ (рис. 3).

Готовые работы на аналогичную тему

Рисунок 3. Прямая в декартовой системе координат

Так как прямая $l$ — серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.

Найдем длины данных сторон по формуле расстояния между точками:

Обозначим через $a=2\left(x_1-x_2\right),\ b=2\left(y_1-y_2\right),\ c=^2+^2-^2-^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:

Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=\$, тогда

Если прямая $l$ параллельна оси $Ox$, то она имеет вид

Если прямая $l$ параллельна оси $Oy$, то она имеет вид

Пример задачи на нахождение уравнений линий в декартовой системе координат

Найти уравнение окружности с центром в точке $(2,\ 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.

Решение.

Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2,\ 4)$, получим

Найдем радиус окружности как расстояние от точки $(2,\ 4)$ до точки $(0,0)$

Получаем, уравнение окружности имеет вид:

Найдем теперь уравнение окружности, используя частный случай 1. Получим

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 05 04 2021

Геометрия. 9 класс

Конспект
Введём уравнение произвольной линии.
В прямоугольной системе координат рассмотрим произвольную линию L.

Уравнение с двумя переменными х и у называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Рассмотрим точки М и N в координатной плоскости.
y = f (x) – уравнение линии L, если выполняются условия:
М (х₁; у₁) ∈ L → y₁ = f (x₁)
N (х₂; у₂) ∉ L → y₂ ≠ f (x₂)
Теперь, зная метод координат и геометрические свойства окружности, выведем её уравнение.
Пусть в прямоугольной системе координат дана окружность, где C – центр окружности с координатами x₀ и y₀, а r – её радиус.
Расстояние от произвольной точки М с координатами х и у до точки С вычисляется по формуле:
Точка М лежит на окружности, то есть координаты точки М удовлетворяют этому уравнению. Значит, МС = r, MC₂ = r₂.
В прямоугольной системе координат уравнение окружности радиуса r и с центром (x — x₀) 2 + (y — y₀) 2 = r 2 имеет вид:
Если центр окружности находится в начале координат, то уравнение окружности с центром в начале координат будет выглядеть так:
Теперь выведем уравнение прямой. Снова рассмотрим прямоугольную систему координат.
Докажем, что любая прямая в декартовых координатах имеет уравнение ax + by + c = 0, где а, b, с – некоторые числа, а х и у – переменные координаты точки А, принадлежащей прямой.
Как и при составлении уравнения окружности, обратимся к свойству прямой, равноудаленной от двух данных точек. Пусть h – произвольная прямая на плоскости и точка А с координатами х и у – точка этой прямой. Точки В и С равноудалены от прямой h, точка D – это точка пересечения ВС с прямой h. Поэтому h – срединный перпендикуляр к отрезку ВС. Так как АС = АВ, то AС₂ = АB₂, значит координаты точки А удовлетворяют уравнению (х – хв)² + (у – ув)² = (х – хс)² + (у – ус)², где В (хв; ув) и С (хс; ус)
Следовательно, это уравнение и является уравнением прямой h в прямоугольной системе координат.
После алгебраических преобразований получаем уравнение прямой: ах + bу + с = 0, где a, b, c некоторые числа. Так как В и С различные точки, значит разность их координат не равна нулю.
Таким образом, уравнение прямой в прямоугольной системе координат является уравнением первой степени.

НАШИ ПАРТНЁРЫ

© Государственная образовательная платформа «Российская электронная школа»