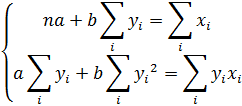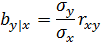Общий вид уравнения прямолинейной регрессии

Прямолинейная регрессия

Дата добавления: 2014-05-02 ; просмотров: 1952 ; Нарушение авторских прав

Это наиболее простой вид регрессии, поэтому неудивительно, что если есть возможность каким-либо способом свести криволинейную регрессию к прямолинейной, то такая возможность используется. Наиболее часто при этом применяется изменение масштаба для одной или обеих переменных, например, путем замены величин на их логарифмы, квадраты, квадратные корни и пр. Подобрав способ преобразования, следует убедиться, что регрессионный анализ может быть применен к полученным преобразованным данным.

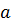
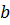
Для отыскания двух параметров и в уравнении регрессии вида:

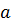
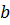
нужно иметь систему из двух уравнений. При использовании метода наименьших квадратов коэффициенты и находятся путем решения системы следующих уравнений:

где п – число пар сопряженных точек.

Из этой системы следует, что:

.

Для нашего примера в итоге получаем (размерность х — %, а у — кал/г грунта):

X	y	x 2	xy

,

.

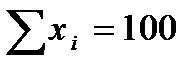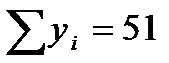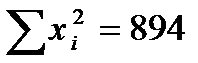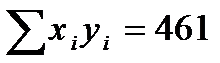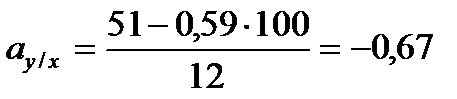
Пользуясь уравнением регрессии можно установить, чему, в среднем, равно значение зависимой переменной при заданном значении независимой переменной. Если коэффициенты в уравнении являются оценками, как это обычно и бывает, то результат вычислений будет оценкой условного среднего. Так, при х = 5,0 получим 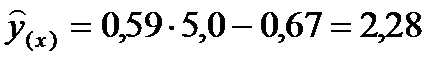кал/г.

Всякое уравнение регрессии имеет границы применимости:

§ Только для данного объекта;

§ Только в заданном интервале изменения аргумента.

Коэффициент 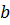характеризует прирост функционального признака при изменении признака, считаемого аргументом, на единицу и, таким образом, является размерной величиной. Ее размерность представляет собой отношение размерности функционального признака к размерности признака, взятого как аргумент. В нашем примере: .

Если регрессионный анализ проводится на корреляционной модели, то в качестве аргумента может быть выбран как признак х, так и признак у. Этим случаям соответствуют два разных уравнения регрессии:

– для y по x

– для x по y

где _y/x характеризует изменение у по х, а _x/y – х по у.

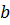
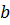
Нахождение параметров а_x/y и в_y/x осуществляется с помощью уже приведенных выражений, в которых индексы х заменены на у.

Для нашего примера:

При корреляционных связях абсолютная величина любого коэффициента регрессии всегда меньше обратной величины другого:

в силу чего эти коэффициенты и именуются коэффициентами регрессии (от латинского regressio — движение назад), и различия эти тем значительнее, чем сильнее изучаемая связь отличается от прямолинейной функциональной зависимости.

Графически:

т.е. чем меньше связь между изучаемыми признаками, тем больше различие между направлениями линий регрессии. В случае полного отсутствия связи (признаки варьируют независимо) теоретические линии регрессии оказываются взаимно перпендикулярными, идущими параллельно осям координат (поскольку b_x/y = b_y/x = 0).

Соответствующая этой зависимости теоретическая линия регрессии х/у) не совпадает с линией регрессии у/х, и в этом проявляется специфика корреляционной связи. Чем меньше степень линейной связи, тем больше угол между линиями регрессии. При r = 0 линии регрессии х/у и у/х оказываются взаимно перпендикулярными и идущими параллельно осям координат. При строго функциональной связи (|r| = 1) линии регрессии сливаются в одну.

Если известно значение коэффициента корреляции r_xy, то значение коэффициента регрессии можно вычислить по формулам:

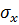
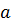
где и — средние квадратичные отклонения для Х и У. Параметр в уравнении регрессии в этом случае будет определяться согласно выражениям:

где и – средние арифметические для признаков Х и У.

Коэффициент корреляции и оба коэффициента регрессии всегда имеют один знак.

Кроме того, полезно заметить, что коэффициент корреляции:

есть среднее геометрическое из коэффициентов регрессии.

Прямолинейная регрессия, ее коэффициент и уравнение

ПРЯМОЛИНЕЙНАЯ РЕГРЕССИЯ, ЕЕ КОЭФФИЦИЕНТ И УРАВНЕНИЕ

При линейном типе связи между двумя изучаемыми признаками кроме расчета корреляций применяется расчет коэффициента регрессии.

В случае прямолинейной корреляционной связи каждому из изменений одного признака соответствует вполне определенное изменение другого признака. Однако коэффициент корреляции показывает эту связь лишь в относительных величинах — в долях единицы. С помощью же регрессионного анализа эту величину связи получают в именованных единицах. Та величина, на которую в среднем изменяется первый признак при изменении второго на единицу измерения, называется коэффициентом регрессии.

В отличие от корреляционного регрессионный анализ дает более широкую информацию, поскольку вычислением двух коэффициентов регрессии Rx/y и Rу/х возможно определить как зависимость первого признака от второго, так и второго от первого. Выражение регрессионной связи с помощью уравнения позволяет по определенному значению одного признака установить значение другого признака.

Коэффициент регрессии R представляет собой произведение коэффициента корреляции на отношение квадратических отклонений, вычисленных для каждого признака. Рассчитывается он по формуле

Rx/y = r ´

где, R — коэффициент регрессии; SХ — среднее квадратическое отклонение первого признака, который изменяется в связи с изменением второго; SУ — среднее квадратическое отклонение второго признака в связи с изменением которого изменяется первый признак; r — коэффициент корреляции между этими признаками; х — функция; у — аргумент.

По этой формуле определяется величина значения х при изменении у на единицу измерения. При необходимости обратного расчета можно найти величину у при изменении х на единицу измерения по формуле:

Rу/х = r ´

В этом случае активная роль в изменении одного признака по отношению к другому меняется, по сравнению с предыдущей формулой аргумент становится функцией и наоборот. Величины SX и SY принимаются в именованном выражении.

Между значениями г и R имеется четкая взаимосвязь, выражающаяся в том, что произведение регрессии х по у на регрессию у по х равно квадрату коэффициента корреляции, т. е.

Это свидетельствует, что коэффициент корреляции представляет собой среднюю геометрическую из обоих значений коэффициентов регрессии данной выборки. Данная формула может быть использована для проверки правильности расчетов.

При обработке цифрового материала на счетных машинах могут применяться развернутые формулы коэффициента регрессии:

Rx/y =;

Rx/y =

Для коэффициента регрессии может быть рассчитана его ошибка репрезентативности. Ошибка коэффициента регрессии равна ошибке коэффициента корреляции, умноженной на отношение квадратических отношений:

SR = ´Sr = ´

Критерий достоверности коэффициента регрессии вычисляется по обычной формуле:

tR =

в итоге он равен критерию достоверности коэффициента корреляции:

tR = = = = tr

Достоверность величины tR устанавливается по таблице Стьюдента при n = n — 2, где n — число пар наблюдений.

Предположим, что при расчете коэффициента корреляции между уровнем яйценоскости и массой яиц:

было установлено, что r = -0,46;

для показателя яйценоскости: = 102; S = 7,0; n = 40

для показателя массы яйца: = 56,68; S = 1,94;n = 40

регрессия первого признака по второму равна:

Rx/y = ´(-0,46) = 3,61´(-0,46) = -1,66

Это означает, что увеличение массы яйца на 1 г в данной популяции кур сопровождается уменьшением яйценоскости за 5 мес. на 1,66 яйцо.

Ry/x = ´(-0,46) = 0,277´(-0,46) = -0,127

показывает, что повышение яйценоскости на 1 яйцо за 5-месячный период в данной популяции кур сопровождается уменьшением средней массы яиц на 0,127 г.

По формуле взаимозависимости r и R можно проверить правильность расчета:

(-1,66) ´ (-0,127) = 0,210; (-0,46)2 = 0,210.

Ошибка коэффициента регрессии Rx/y = равна

SR = ´Sr = ´

SR = 3,61´= 3,61´= 3,61´0,144 = 0,52

Критерий достоверности Rx/y равен

tR = = 3,19

По таблице Стьюдента стандартные значения t для n = 38 равны 2,0-2,7-3,6. Следовательно, рассчитанный коэффициент регрессии достоверен при Р ³ 0,99.

Более глубокий анализ связи двух признаков может быть сделан на основе расчета уравнения прямолинейной регрессии. Сущность коэффициента прямолинейной регрессии, показывающей насколько второй признак отклоняется от своей средней, если первый отклоняется от своей средней на единицу измерения, можно выразить формулой

Преобразуя это уравнение, получаем рабочую формулу прямолинейной регрессии. Обозначаем Ry/x через b:

Обозначаем = а, следовательно

В этом уравнении х является аргументом, у — его функцией. Уравнение показывает взаимоотношение между аргументом и функцией, именно то взаимоотношение признаков, которое и образует коэффициент регрессии. По этой формуле, зная значения аргумента (х) можно определить значение его функции (у) без непосредственного ее измерения.

В рассмотренном выше примере были вычислены коэффициенты корреляции и регрессии между уровнем яйценоскости и массой яиц у кур. Если принять яйценоскость кур за аргумент, можно составить следующее уравнение прямолинейной регрессии:

;

а = 56,6,127) ´ 102 = 56,68 + 12,95 – 69,63; а = 69,63

у = 69,63 + (-0,127) ´ x = 69,63 – 0,127 ´ x

Таким образом, для того, чтобы установить, какая масса яйца может соответствовать тому или иному уровню яйценоскости, нужно умножить показатель яйценоскости на коэффициент 0,127 и вычесть это произведение из числа 69,63. На основе этого уравнения можно заранее рассчитать значение функций для каждого значения аргумента. Таким образом, в частности в данном примере, можно составить ряд, показывающий регрессионные зависимости яйценоскости и массы яиц в данной популяции кур.

Теоретический ряд регрессии между признаками яйценоскости кур

Уравнение регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 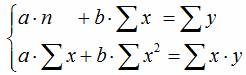. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида: