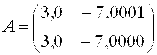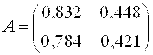Обусловленность систем линейных уравнений
Две на первый взгляд похожие системы линейных уравнений могут обладать различной чувствительностью к погрешностям задания входных данных. Это свойство связано с понятием обусловленности системы уравнений.
Числом обусловленности линейного оператора A, действующего в нормированном пространстве 
Таким образом, появляется связь числа обусловленности с выбором нормы.
Предположим, что матрица и правая часть системы заданы неточно. При этом погрешность матрицы составляет dA, а правой части — dу. Можно показать, что для погрешности dx имеет место следующая оценка ( 

В частности, если dA = 0, то
При этом решение уравнения Ax = у не при всех у одинаково чувствительно к возмущению dу правой части.
Свойства числа обусловленности линейного оператора:
1.
причем максимум и минимум берутся для всех таких x, что 
2.
3
где 

4.
Матрицы с большим числом обусловленности (ориентировочно 



Таким образом, погрешность решения, вызванная погрешностями округления, может быть недопустимо большой в случае плохо обусловленных систем.
Итак – принципиально остаются две проблемы –
1.не обеспечивается обоснованная сходимость алгоритма к единственной (в случае модельного примера- истинной) структуре и
2. Не разрешено противоречие о неадекватности моделей шаговой регрессии на новых точках, не участвовавших при оценке параметров модели. Возможно ли, если не обеспечить такую адекватность при других способах синтеза моделей, то хотя бы найти путь к решению такой задачи (возможно и адекватность определить другим способом )
Для АШР даже в случае применения для МНК оценки процедуры Грамма-Шмидта не разрешается вопрос о единственности модели – просто оценки параметров становятся наиболее точными и несмещенными
Т.о. гарантированное нахождение всего множества подходящих решений в реальных задачах (при 
перебора всех подструктур полной структуры как в методе всех регрессий (у Дрейпера и Смита). Тогда мы найдем всете модели, в которых все аргументы входят с уровнем значимости не менее чем заданный. Со всеми выше описанными проблемами – а какая же из них, из этого множества та, которая действительно наша.
Можно еще добавить камень в огород АШР о неиспользуемой возможности вариации уровнем значимости для учета уровня шума в данных
Именно эту проблему предлагает решать МГУА с помощью введения понятия внешних критериев.
Необходимое примечание.
при 
Каждый из них это делает по своему, и определить адекватность метода по сходимости к нужной модели можно только построив соответствующий вашей задаче модельный пример.
Однако наиболее распространенный случай – это когда число точек невелико 




И наиболее эффективный подход к решению структурно-параметрического синтеза при данных условиях демонстрирует МГУА
Как видим нарушение уже первого условия порождаетнеобходимомость разрешения проблемы множественности моделей не прибегая к процедуре полного перебора –надо предложить какой-то принцип, позволяющий найти путь к истинной или квазиистинной модели без полного перебора претендентов моделей.
Следующая проблема не менее реальна и еще более запутывает задачу поиска структуры. – проблема шума в данных –мы помним что при это нарушаются свойства проекционности аппарата МНК – нарушаются свойства оценок, но проблема в том что на зашумленных данных найти истинную структуру вообще может бытььпроблематично – если неизвестны х-ки шума и точки их приложения алгоритм будет тупо подстраиваться под шум.
Основная проблема– проблема необоснованности выбора структуры модели классическими АШГ многократно обостряется в связи с тем что порог используемый критерием Фишера в виде уровня значимости
на самом деле регулирует не только риск ошибки
– его выбор должен учитывать уровень шума и точки его приложения.
Ведь увеличение уровня шума например на выходе неизбено требует загрубить модель (не подстраивать ее под шум) а значит изменить уровень увеличить значимости с тем чтобы более жестко фильтровать апгументы в модель и ее упрощать .
Гораздо сложнее учесть шумы на входе тем более если они проходят нелинейное преобразование модели.
Однако методологически механизмов учета данных коррекций в агоритмах нет что делает выбор структур в условиях шума необоснованным.
Реферат: Численные методы решения систем линейных алгебраических уравнений
| Название: Численные методы решения систем линейных алгебраических уравнений Раздел: Рефераты по математике Тип: реферат Добавлен 07:31:10 24 июня 2011 Похожие работы Просмотров: 3515 Комментариев: 13 Оценило: 4 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| k | х1(k) | х2(k) | х3(k) |
| 0 | 1.0 | 2.0 | 2.0 |
| 1 | 1.75 | 3.375 | 3.0 |
| 2 | 1.84375 | 3.875 | 3.025 |
| 3 | 1.9625 | 3.925 | 2.9625 |
| 4 | 1.990625 | 3.9765625 | 3.0 |
| 5 | 1.99414063 | 3.9953125 | 3.0009375 |
| … | … | … | … |
| 15 | 1.99999993 | 3.99999985 | 3.0009375 |
| … | … | … | … |
| 19 | 2.0 | 4.0 | 3.0 |
Этот процесс называется итерацией Якоби и может использоваться для решения определенных типов линейных систем [19].
1.5 Итерация Гаусса-Зейделя
Процесс итерации Якоби иногда можно модифицировать для ускорения сходимости.
Отметим, что итеративный процесс Якоби производит три последовательности – <х1 (k) >, <х2 (k) >, <х3 (k) >, <х4 (k) >. Кажется разумным, что х1 (k+1) может быть использовано вместо х2 (k ). Аналогично х1 (k+1) и х2 (k+1) можно использовать в вычислении х3 (k+1) . Например, для уравнений из системы (1) это даст следующий вид итерационного процесса Гаусса-Зейделя, использующий (3*):
Такой итерационный процесс даст результаты:
| k | х1 (k) | х2 (k) | х3 (k) |
| 0 | 1.0 | 2.0 | 2.0 |
| 1 | 1.75 | 3.75 | 2.95 |
| 2 | 1.95 | 3.96875 | 2.98625 |
| 3 | 1.995625 | 3.99609375 | 2.99903125 |
| … | … | … | … |
| 8 | 1.99999983 | 3.99999988 | 2.99999996 |
| 9 | 1.99999998 | 3.99999999 | 3.0 |
| 10 | 2.0 | 4.0 | 3.0 |
Т. е. к точному решению мы пришли уже на 10-ом шаге итерации, а не на 19, как в итерации Якоби [19].
1. Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы. Для этого система приводится к виду (для случая системы из четырех уравнений):
Эти формулы как раз и задают собственно итерационный процесс.
2. При этом чтобы итерационный процесс сходился к точному решению, достаточно, чтобы все коэффициенты системы были малы по сравнению с диагональными.
Это условие можно сформулировать и более точно:
Для сходимости процесса итераций достаточно, чтобы в каждом столбце сумма отношений коэффициентов системы к диагональным элементам, взятым из той же строки, была строго меньше единицы:
3. Следует так же сказать, что итерационный процесс может проводиться как в виде итерации Якоби, так и в виде итерации Гаусса-Зейделя. В последнем случае сходимость итерационного процесса может существенно улучшиться.
Глава 2. Применение численных методов для решения систем линейных алгебраических уравнений в теории и на практике
§1 ЧИСЛЕННЫЕ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Существуют два типа методов — прямые и итерационные. Мы рассматриваем прежде всего метод исключения Гаусса для систем общего вида и варианты — метод прогонки и методы матричной прогонки для систем специального вида (с трех-диагональной или блочно-трех диагональной матрицами). Это — прямые методы. Их эффективность зависит от порядка системы n структуры матрицы.
При изучении итерационных методов мы трактуем систему уравнений как операторное уравнение первого рода Au = f и излагаем общую теорию итерационных методов для операторных уравнений при минимальных предположениях относительно оператора А. Общая теория позволяет доказать сходимость итераций для метода Зейделя и метода верхней релаксации при минимальных ограничениях на оператор А. Рассмотрены два класса методов: 1) для случая, когда известны границы γi > О и γ2 >= γ1 спектра оператора А в некотором энергетическом пространстве HD ; 2) для случая, когда границы γ1 и γ2 неизвестны. Весьма эффективным является попеременно-треугольный метод.
Основная задача линейной алгебры — решение системы уравнений
Будем предполагать, что матрица А невырождена, так что уравнение Аи = 0 имеет только тривиальное решение, и система (1) имеет единственноерешение
В курсе линейной алгебры решение системы (1) обычно выражают по формулам Крамера в виде отношений определителей. Для численного решения системы (1) эти формулы непригодны, так как они требуют вычисления N +1 определителей, что требует большого числа действий (порядка N! арифметических операций). Даже при выборе наилучшего метода вычисление одного определителя требует примерно такого же времени, что и решение системы линейных уравнений современными численными методами. Кроме того, следует иметь в виду, что вычисления по формулам Крамера часто ведут к большим ошибкам округлений.
Особенность большинства численных методов для (1) состоит в отказе от нахождения обратной матрицы. Основное требование к методу решения — минимум числа арифметических действий, достаточных для отыскания приближенного решения с заданной точностью е>0 (экономичность численного метода).
Выбор того или иного численного метода зависит от многих обстоятельств — от имеющихся программ, от вида матрицы А, от типа расчета и др. Поясним слова «тип расчета». Возможны разные постановки задачи:
1) найти решение одной конкретной задачи (1);
2) найти решение нескольких вариантов задачи (1) с одной и той же матрицей А и разными правыми частями. Может оказаться, что неоптимальный для одной задачи метод является весьма эффективным для многовариантного расчета.
При многовариантном расчете можно уменьшить среднее число операций для одного варианта, если хранить некоторые величины, а не вычислять их заново для каждого варианта. Это, конечно, зависит от машины, от объема ее оперативной памяти.
При теоретических оценках качества алгоритмов их сравнение проводится по числу q ( e ) арифметических действий, достаточных для нахождения решения задачи с заданной точностью е > 0 [15].
Метод Гаусса. Имеется несколько вычислительных вариантов метода Гаусса, основанного на идее последовательного исключения. Процесс решения системы линейных алгебраических уравнений Ax = f (1) по методу Гаусса состоит из двух этапов.
Первый этап (прямой ход). Система (1) приводится к треугольному виду
Метод квадратного корня. Этот метод пригоден для систем
с эрмитовой (в действительном случае — симметричной) матрицей А. Матрица А разлагается в произведение
где S — верхняя треугольная, D — диагональная матрица. Решение уравнения Аu=fсводится к последовательному решению двух систем
Метод квадратного корня требует порядка N 2 /3 арифметических действий, т. е. при больших N он вдвое быстрее метода Гаусса и занимает вдвое меньше ячеек памяти. Это обстоятельство объясняется тем, что метод использует информацию о симметрии матрицы.
1. Метод итераций для решения системы линейных алгебраических уравнений .
Перейдем к общему описанию метода итераций для системы линейных алгебраических уравнений
Для ее решения выбирается некоторое начальное приближение у0 
Важную роль играет запись итерационных методов в единой (канонической) форме. Любой двухслойный итерационный метод можно записать в следующей канонической форме:


Если В = Е — единичный оператор, то метод(8) называют явным: yh +1 находится по явной формуле
В общем случае, при В≠ Е, метод (7) называют неявным итерационным методом: для определения yh +1 надо решить уравнение:

Естественно требовать, чтобы объем вычислений для решения .системы Byk +1 = Fk был меньше, чем объем вычислений для прямого решения системы Au=f
Точность итерационного метода (7) характеризуется величиной погрешности zh = ук — и, т. е. разностью между решением уравнения (7) и точным решением и исходной системы линейных алгебраических уравнений. Подстановка yk = zk + u в (2) приводит к однородному уравнению для погрешности:
§2 ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
2.1 Общие сведения
К численным методам линейной алгебры относятся численные методы решения систем линейных алгебраических уравнений. Методы решения СЛАУ разбиваются на две группы. К первой группе принадлежат так называемые точные или прямые методы — алгоритм, позволяющий получить решение системы за конечное число арифметических действий. Вторую группу составляют приближенные методы, в частности итерационные методы решения СЛАУ.
2.2.1 Описание метода
Рассмотрим СЛАУ вида
Ax = B, где А — матрица. (1)
Если эту систему удалось привести к виду x = Cx + D, то можно построить итерационную процедуру
xk → x*, где х* — решение заданной системы.
В конечном варианте система будет имееть вид:
Условием сходимости для матрицы С выполняется, если сумма модулей коэффициентов меньше единицы по строкам или по столбцам, т.е.


Необходимо, чтобы диагональные элементы матрицы А были ненулевыми.
Для преобразования системы можно выполнить следующие операции:
В результате получим систему:
В ней на главной диагонали матрицы С находятся нулевые элементы, остальные элементы выражаются по формулам:
Итерационный процесс продолжается до тех пор, пока значения х1 ( k ), х2 ( k ), х3 ( k ) не станут близкими с заданной погрешностью к значениям х1 ( k -1), х2 ( k -1), х3 ( k -1).
2.2.2 Решение СЛАУ методом простых итераций
Решить СЛАУ методом простых итераций с точностью 
Для удобства преобразуем систему к виду:

Принимаем приближение на 0-ом шаге:


На 1-м шаге выполняем следующее:
Подставляем принятые приближения в первоначальную систему уравнений
Смотрим не выполняется ли условие остановки итерационного процесса:

На 2-м шаге выполняем следующее:
Смотрим не выполняется ли условие остановки итерационного процесса

На 3-м шаге выполняем следующее:
Смотрим не выполняется ли условие остановки итерационного процесса

На 4-м шаге выполняем следующее:
Смотрим не выполняется ли условие остановки итерационного процесса

На 5-м шаге выполняем следующее:
Смотрим не выполняется ли условие остановки итерационного процесса:

На 6-м шаге выполняем следующее:
Смотрим не выполняется ли условие остановки итерационного процесса:

Необходимая точность достигнута на 6-й итерации. Таким образом, итерационный процесс можно прекратить [14].
2.3 Метод Зейделя
2.3.1 Описание метода
В этом методе результаты, полученные на k-том шаге, используются на этом же шаге. На (k+1) — й итерации компоненты приближения 
Этот метод применим к система уравнений в виде Ax=B при условии, что диагональный элемент матрицы коэффициентов A по модулю должен быть больше, чем сумма модулей остальных элементов соответствующей строки (столбца).
Если данное условие выполнено, необходимо проследить, чтобы система была приведена к виду, удовлетворяющему решению методом простой итерации и выполнялось необходимое условие сходимости метода итераций:

2.3.2 Решение СЛАУ методом Зейделя
Решить СЛАУ методом Зейделя с точностью 
Эту систему можно записать в виде:
В этой системе сразу видно, что выполняется условие, где диагональные элементы матрицы коэффициентов по модулю больше, чем сумма модулей остальных элементов соответствующей строки.
Для удобства преобразуем систему к виду:

Принимаем приближение на 0-ом шаге:
На 1-м шаге выполняем следующее:
Подставляем принятые приближения в первоначальную систему уравнений
Смотрим не выполняется ли условие остановки итерационного процесса

На 2-м шаге выполняем следующее:
Смотрим не выполняется ли условие остановки итерационного процесса

На 3-м шаге выполняем следующее:
Смотрим не выполняется ли условие остановки итерационного процесса:

На 4-м шаге выполняем следующее:
Смотрим не выполняется ли условие остановки итерационного процесса

Необходимая точность достигнута на 4-й итерации. Таким образом, итерационный процесс можно прекратить [9].
2.4 Сравнительный анализ
Можно заметить, что в методе Зейделя быстрее мы достигаемой нужной точности, в нашем случае в точность была достигнута на 4-й итерации, когда в методе простых итераций она была достигнута на 6-й итерации. Но в то же время в методе Зейделя ставится больше условий. Поэтому вначале нужно произвести иногда довольно трудоемкие преобразования. В таблице 4.1 приведены результаты решения СЛАУ методом простой итерации и методом Зейделя на различных шагах итерации:
6.1. Решение систем линейных алгебраических уравнений. Обусловленность матрицы
При исследовании численных методов для решения математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма. Для каждой математической задачи принято рассматривать вопрос о ее корректности.
Определение. Говорят, что задача поставлена корректно, если ее решение существует, единственно и непрерывно зависит от входных данных.
Где А — квадратная, неособенная матрица размерности N, и, следовательно, det(A) ≠ 0, тогда существует единственное решение системы. Чтобы убедиться в корректности задачи (6.1) необходимо еще установить непрерывную зависимость решения от входных данных. Входными данными являются правая часть F и элементы матрицы А.
Соответственно, различают устойчивость по правой части, когда возмущается только правая часть F , а матрица А остается неизменной, и коэффициентную устойчивость, когда возмущается только матрица А .
Будем считать, что решение и правая часть задачи (6.1) принадлежат линейному пространству H, состоящему из N-мерных векторов. Введем в H норму, для которой выполнено:
||X||>0, для всех Х≠0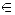
||α X||=| α| ||X||, для любого числа А и Х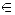
||X+Y||≤||X||+||Y||, для любых X и Y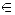
Определение. Нормой матрицы А, подчиненной данной норме векторов, называется число 
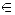
Наряду с системой (6.1) рассмотрим «возмущенную» систему A Xε = Fδ , которая отличается от (6.1) правой частью. Насколько сильно может измениться решение Х В результате изменения правой части?
Определение. Говорят, что система (6.1) устойчива по правой части, если при любых F и Fδ Справедлива оценка || δx||≤ M || δf ||, где M — постоянная, M >0.
Эта оценка выражает факт непрерывной зависимости решения от правой части, то есть показывает, что || δx|| Стремится к нулю при || δf ||Стремящемся к нулю. Наличие устойчивости очень важно при численном решении систем уравнений, так как никогда нельзя задать правую часть F точно. Погрешность δf возникает в результате округления.
Получим оценку для относительной погрешности решения 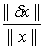
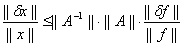
Определение. Число ρ(A)= 
ρ(A)=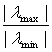
Где λMax , λmin – максимальное и минимальное по модулю собственные значения матрицы A.
Матрицы с большим числом обусловленности называются плохо обусловленными. При численном решении систем с такими матрицами возможно сильное накопление погрешности. При небольших изменениях правой части погрешность решения может оказаться значительной.
Например, для матрицы
Число обусловленности ρ(A)=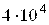
Если взять матрицу
И за правую часть системы вектор F= (1,0000, 0)T, то получим решение 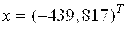
http://www.bestreferat.ru/referat-238943.html
http://matica.org.ua/metodichki-i-knigi-po-matematike/metody-vychislenii-o-n-gavrishina-m-r-ekimova-l-n-fomina/6-1-reshenie-sistem-lineinykh-algebraicheskikh-uravnenii-obuslovlennost-matritcy