Одномерное движение свободной частицы уравнение
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
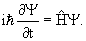 | (4.1) |
где 
в которой 







х → 


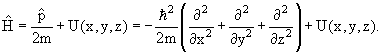 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


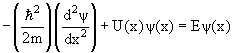
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
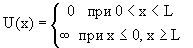 | (4.5) |
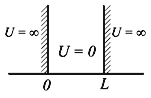
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
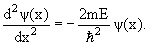 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
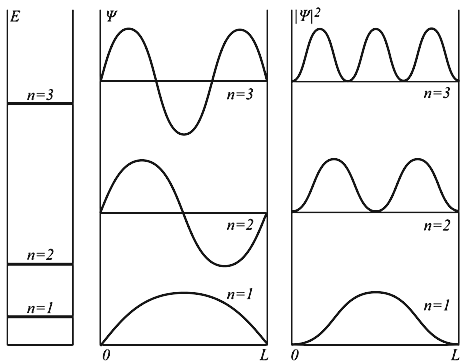
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
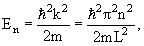 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
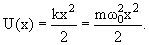 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
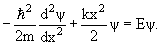 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
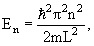

Одномерный гармонический осциллятор:
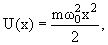
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
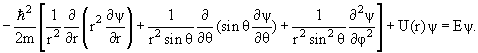 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
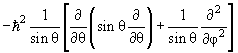 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 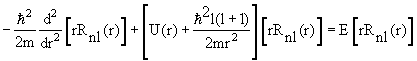 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
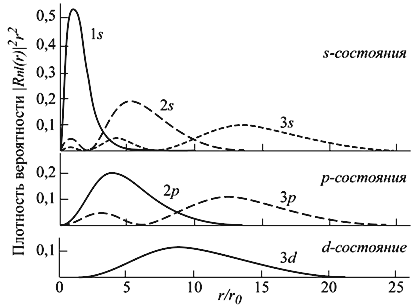
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
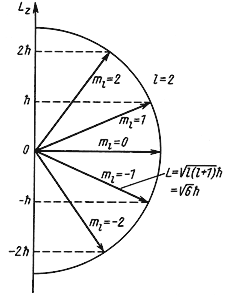
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
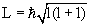 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
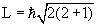
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Одномерное движение свободной частицы уравнение
Корпускулярно-волновой дуализм. Уравнение Шрёдингера
План
- Экспериментальное обоснование основных идей квантовой теории
- Коротковолновая граница сплошного рентгеновского спектра
- Опыт Боте
- Связь между волновой и корпускулярной картинами
- Гипотеза де Бройля
- Микрочастица в двухлучевом интерферометре
- Соотношение неопределённостей
- Волновая функция, её вероятностная интерпретация и свойства
- Уравнение Шрёдингера
- Нестационарное (временное) уравнение Шрёдингера
- Стационарное уравнение Шрёдингера
- Собственные функции, собственные значения
- Применение уравнения Шрёдингера
- Одномерное движение свободной частицы
- Частица в одномерной потенциальной яме с бесконечно высокими стенками
- Линейный гармонический осциллятор
а) Классический
1. Экспериментальное обоснование основных идей квантовой теории
Волновые свойства света проявляются в явлениях:
- интерференции,
- дифракции,
- поляризации.
Явления:
- фотоэффекта,
- комптоновского рассеяния,
- тепловое излучение
могут быть объяснены только корпускулярными свойствами.
Давление света можно объяснить и с точки зрения волновой, и корпускулярной теории.
К экспериментальному обоснованию квантовых свойств относятся:
- существование коротковолновой границы сплошного рентгеновского спектра;
- опыт Боте.
1.1. Коротковолновая граница сплошного рентгеновского спектра
R



Рис.21.2

Не привлекая гипотезу о квантах излучения с энергией

не удаётся объяснить существование коротковолновой границы тормозного спектра.
Этот опыт должен был дать ответ на вопрос, как же происходит электромагнитное излучение: как волна или как поток дискретных частиц – фотонов.
М
еталлическая фольга облучается рентгеновским излучением и сама, в свою очередь, становится источником рентгеновского излучения (рис.21.3). Счётчики Гейгера, расположенные симметрично, фиксируют вторичные R-лучи. Если бы вторичное излучение распространялось в виде сферических волн, оба счётчика должны срабатывать одновременно, и на ленте самописца отметки слева и справа совпадали бы. Опыт дал другие результаты: счётчики срабатывали случайным образом, неодновременно. Это значит, что при излучении возникали отдельные фотоны, попадавшие либо в один счётчик, либо в другой.
2. Связь между волновой и корпускулярной картинами
Таким образом, оказалось, что свет обнаруживает корпускулярно-волновой дуализм: обладает и свойствами волн, и свойствами частиц. Эти свойства с макроскопической точки зрения противоречат друг другу: волна непрерывна, частица – дискретна; волна – безгранична, частица – ограничена в пространстве. Как совместить эти противоречащие друг другу свойства? Эта задача была решена. Установить связь между волновой и корпускулярной картинами можно с помощью статистического подхода.
Запишем уравнение электромагнитной волны (Е – напряжённость электрического поля волны; Е0 – амплитуда):

Тогда вероятность dp того, что фотон будет обнаружен в малом объёме 




Здесь 
Таким образом, распределение фотонов носит статистический характер. Квадрат амплитуды волны определяет вероятность попадания фотона в данную точку.
3. Гипотеза де Бройля
В 1923 г. Луи де Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм универсален, то есть частицы обладают волновыми свойствами. Существует симметрия: если свет (волна) обладает корпускулярными свойствами, то почему бы частицам не проявлять свойства волновые? Природа едина.
Короче, всем частицам (фотонам, протонам, электронам, нейтронам, атомам, молекулам,…) приписываем
- корпускулярные свойства (энергию
и импульс
) и
- волновые свойства (длину волны
и частоту
).
При этом длина волны связана с импульсом для любой частицы так же, как и для фотона (см. лекцию № 20):

Это – длина волны де Бройля.
Для любой частицы справедливы соотношения:
| Корпускулярные свойства | Волновые свойства |
 |  |
 |  |
Движущейся частице с импульсом 







Для волны, бегущей вдоль оси OX (частицы, движущейся параллельно оси OX):

(Смысл функции 
Подтверждение гипотезы де Бройля было получено экспериментально (1927 год) при наблюдении дифракции электронов:
- Опыты Дэвиссона и Джермера. Отражение электронов от кристалла никеля подчиняется формуле Брэгга-Вульфа (см. лекцию № 18):

- В
опытах Дж.Томсона исследовалась дифракция электронов на тонкой металлической поликристаллической фольге (рис.21.4). На фотопластинке появлялась дифракционная картина в виде концентрических колец, опять же в соответствии с формулой Брэгга-Вульфа.
Электроны, ускоренные в электрическом поле разностью потенциалов U, имеют энергию

Тогда длина волны де Бройля

Совпадение длин волн, предсказанных де Бройлем по (21.10) и полученных из эксперимента по (21.9), совпали с точностью до 1%. Волновые свойства электрона обнаружились и в других экспериментах. Более того, удалось наблюдать дифракцию н
Замечательно, что волновые свойства присущи каждой частице: дифракционная картина наблюдается и в случае очень слабых пучков, когда частицы летят поодиночке. На рис.21.6 (а, б, в, г) видно, как со временем по мере выпуска всё новых и новых молекул на финальной пластине всё ярче и ярче проступает интерференционная картина. Благодаря дифракции случайно прибывающие на финиш массивные частицы проявляют свои волновые свойства.
4
И
ллюстрацией двойственности свойств микрочастиц является опыт с двухщелевым интерферометром. Диафрагма с двумя щелями обстреливается потоком микрочастиц (электронов), которые затем попадают на экран (рис.21.7, а). Если открыта одна щель, напротив неё на экране получается полоса (рис.21.7,а). Открывая вторую щель, ожидаем получить на экране две полосы, то есть простое сложение картинок при одной и второй открытой щелях (рис.21.7,б), как это было бы в макромире при обстреле диафрагмы с щелями обычными пулями. Но в опытах микрочастицами на экране появляется типичная интерференционная картина (рис.21.8), характерная для световых волн в аналогичном опыте Юнга. Электроны интерферируют при прохождении через две щели.
Пули дискретны, неделимы: каждая проходит через какую-то одну из двух щелей; никакой интерференции нет.
Электрон, как и пуля, дискретен, он не может разделиться и пройти одновременно через обе щели. Проделаем тот же эксперимент с волнами (рис.21.9): волна проходит через обе щели, она непрерывна. Для волн нет дискретности; есть интерференция.
Э
Могло создаться впечатление, что микрочастицы интерферируют, потому что взаимодействуют друг с другом. Но даже для очень слабых пучков, когда микрочастицы летят поодиночке, интерференционная картина рис. 21.8, б, сохранялась, только нужно было подождать достаточно долго, чтобы картина достаточно проявилась. Электроны как будто «знают», что открыты обе щели, и попадают в нужные места экрана: туда, где должны быть интерференционные максимумы. Электрон интерферирует сам с собой? На движение одиночного, дискретного и неделимого электрона оказывают влияние обе щели.
Как это понять? Приходится принять, что микрочастица обладает принципиально иными свойствами, чем макрочастица. У микрочастиц нет траектории.
Электрон не может «разделиться» на половинки и пролететь сразу через обе щели. Всё-таки хотелось бы знать, через какую щель пролетел электрон. «Подсмотрим» за электроном, поставив сразу за каждой из щелей источник света. Электрон, прошедший через данную щель, будет рассеивать свет, и мы это «увидим», то есть будем точно знать, через какую из щелей прошёл электрон; а если он, разделившись, пройдёт сразу через две щели, вспышки у каждой из щелей произойдут одновременно. В этом эксперименте получили, что электрон проходит только либо через одну щель, либо только через вторую. Но при этом никакой интерференции нет (рис.21.10). Выключаем источники света, и картинка интерференции появляется снова (рис. 21.8, б).
Е

Если будем фиксировать, через какую щель прошёл электрон (включили лампочку), то не получим интерференции. Если знаем координату электрона (пролетел через данную щель), то не знаем длину волны, не знаем импульс.
5. Соотношение неопределённостей
Из корпускулярно-волнового дуализма микрочастиц вытекает, что нельзя одновременно точно знать её координату и импульс. Нельзя сказать: длина волны в данной точке; волна – протяжённый в пространстве объект. Если точно знаем импульс частицы, то знаем длину волны де Бройля (21.6):

можем записать волновое уравнение (21.7), но совершенно не знаем, где находится наша частица: гармоническая волна в пространстве бесконечна.
В 1927 году подобные соображения были сформулированы Гейзенбергом в виде принципа неопределённостей:
Произведение неопределённостей координаты и соответствующей проекции импульса частицы не меньше 


Аналогично, для осей OY и OZ:


Существуют пары физических величин, которые, подобно импульсу и координате, нельзя измерять одновременно точно. Такие величины называются сопряжёнными динамическими переменными. Это время и энергия; момент импульса и угловая координата. Запишем принцип неопределённостей для таких сопряжённых величин:


Здесь 

Принцип неопределённостей Гейзенберга не связан с несовершенством приборов или методов измерения; является спецификой микрочастиц – проявлением корпускулярно-волнового дуализма.
6. Волновая функция, её вероятностная интерпретация и свойства
Квантовая механика была создана в начале 20-го века. В ней учитываются волновые свойства микрочастиц. Авторы квантовой механики: Планк, Гейзенберг, Шрёдингер, Борн.
Состояние микрообъекта в квантовой механике описывается волновой функцией (пси-функция) 
Смысл функции: квадрат модуля волновой функции определяет вероятность нахождения частицы в данной точке, то есть вероятность dp обнаружить частицу в объёме dV вблизи заданной точки с координатами x, y, z в момент времени t равна


где 
Плотность вероятности обнаружения частицы в данной точке равна квадрату модуля волновой функции:

Свойства волновой функции:
- Однозначна, конечна, непрерывна, дифференцируема.
- Вероятность pV найти частицу в конечном объёме V равна (из (21.12)):

- Вероятность найти частицу хотя бы где-нибудь: неважно, в какой точке пространства – достоверное событие (если частица существует); поэтому сумма всех вероятностей по всему пространству есть единица:

Это – условие нормировки. Уточнение: интеграл в (21.15) берётся по всей области определения функции.
- Волновую функцию можно домножить на любое комплексное число С, и полученная функция будет описывать то же самое состояние:
и
описывают одинаковые состояния частицы.
- Если частица может находиться в состоянии, описываемом функциями
, или
, …, или
, то возможно состояние частицы, описываемое любой линейной комбинацией этих функций:

где 
- Зная волновую функцию состояния, можно найти среднее значение любой физической величины В:

Описание состояния частицы с помощью волновой функции не позволяет найти ни координаты частицы, ни её траекторию. Однако утверждается, что волновая функция даёт исчерпывающее описание поведения микрочастицы. Волновая функция не даёт информации о том, чего нет: у микрочастиц нет траектории, нет точных значений координат в любой момент времени.
7. Уравнение Шрёдингера
7.1. Нестационарное (временное) уравнение Шрёдингера
Уравнение Шрёдингера – основное уравнение квантовой механики. Оно получено в 1926 году. Решением уравнения Шрёдингера получают волновую функцию состояния 
Временное уравнение Шрёдингера:

Здесь 






7.2. Стационарное уравнение Шрёдингера
Оказывается, что если 





поскольку временная часть не зависит от координат, а в оператор Лапласа входят только частные производные по координатам. Далее,

Подставляем (21.21) и (21.22) во временное уравнение Шрёдингера (21.18) и сокращаем на 


Полная энергия частицы по (21.7) 



Это – стационарное уравнение Шрёдингера.
7.3. Собственные функции, собственные значения
Решение уравнения Шрёдингера существует не для любых значений энергии Е. Значения энергии, при которых решение существует, называются собственными значениями. Соответствующие им волновые функции 
Совокупность собственных значений энергии – спектр (энергетический спектр). Спектр энергии может быть дискретным (набор конкретных значений) или непрерывным, сплошным. Если спектр дискретный, собственные значения можно пронумеровать:




Этим значениям соответствуют собственные функции:



Возможен вариант, когда одному и тому же собственному значению энергии соответствует несколько волновых функций; например, три:

Тогда соответствующий уровень энергии называется вырожденным, причём кратность вырождения равна числу волновых функций. В приведённом примере уровень 
Замечание: Квантование энергии при решении уравнения Шрёдингера получается естественно, без привлечения каких-либо дополнительных соображений.
8. Применение уравнения Шрёдингера
8.1. Одномерное движение свободной частицы
Пусть частица движется в постоянном потенциальном поле, причём потенциальная энергия частицы меньше её полной энергии:

Рассматривается одномерное движение вдоль оси OX, тогда волновая функция зависит только от координаты x (




Это обыкновенное дифференциальное однородное уравнение второго порядка; его решением, в частности, будет гармоническая функция:

Здесь 

Запишем общее решение, помня, что волновая функция 



Получили суперпозицию двух волн: первое слагаемое представляет собой волну, бегущую в положительном направлении оси OX, второе – в отрицательном.
Действительная часть пси-функции – это суперпозиция двух косинусов (по формуле Эйлера 

8.2. Частица в одномерной потенциальной яме с бесконечно высокими стенками
Рассмотрим частицу в одномерной потенциальной яме шириной l с бесконечно высокими стенками, то есть потенциальная энергия частицы U обращается в бесконечность при 


З




Осталось записать и решить уравнение Шрёдингера на интервале 


Вводим обозначение для волнового числа:


Решение этого уравнения имеет смысл записать в виде синуса; тогда автоматически удовлетворим требованию непрерывности волновой функции на левом конце интервала ( 

Должно также выполняться условие:



Здесь n – квантовое число; оно может принимать значения
Для энергии из (21.25):


Получено квантование энергии: энергия частицы может принимать только дискретные значения (рис.21.12), которые даёт соотношение (21.28). Минимальное значение энергия принимает при 

Минимальное значение энергии не может быть равным нулю в силу принципа неопределённостей.
Из (21.27) и (21.28) получим соответствующие этим уровням энергии волновые функции:

При 
при 
при 
и т.д. (см. графики функций рис.21.13).
А
мплитуду А волновой функции находим из условия нормировки (21.15):







Расстояние между соседними уровнями энергии из (21.29):

Относительное расстояние между уровнями уменьшается при увеличении квантового числа n:

Для больших квантовых чисел n дискретность уровней энергии уже не играет роли; относительное расстояние между ними уменьшается. Это – проявление принципа соответствия: при больших квантовых числах (большая энергия) законы квантовой механики дают тот же результат, что и классическая механика; энергию можно считать изменяющейся непрерывно.
Рассчитаем расстояние между уровнями энергии при n=1 по (21.31) для электрона в потенциальной яме шириной:
- порядка размера атома
:
- для макротела размером
:

В первом случае дискретность уровней энергии существенна; во втором случае уровни так близки, что энергию можно считать изменяющейся непрерывно.
8.3. Линейный гармонический осциллятор
Классический гармонический осциллятор – например, грузик массой m на пружинке жёсткостью 

Полная энергия сохраняется, только перераспределяется между потенциальной и кинетической:

Максимальное смещение грузика определяется запасом полной энергии системы. Координата x изменяется в пределах:

При небольших деформациях пружины, когда ещё выполняется закон Гука, и справедлива зависимость (21.32), колебания гармонические и происходят по закону:
с циклической частотой, определяемой параметрами системы – массой груза и жёсткостью пружины:


Поскольку в поворотных точках при 

б) Квантовый гармонический осциллятор
Потенциальную энергию квантового осциллятора возьмём в том же виде, как и для классического осциллятора.


Здесь величина 

Решать это уравнение мы не будем; приведём результаты.
Уравнение (21.34) имеет решение не при любых значениях полной энергии E, а только при:

где υ – колебательное квантовое число, принимающее целочисленные значения
Полная энергия не может обращать в ноль; её минимальное значение в основном состоянии системы при

Это – так называемые нулевые колебания, следствие принципа неопределённостей. Волновая функция основного состояния выглядит так:

Все уровни энергии отстоят друг от друга на одинаковом расстоянии (рис.21.15), равном

П


- Вероятность найти частицу за пределами потенциальной ямы в области, запрещённой классической механикой, отлична от нуля, хотя и быстро убывает.
- Для больших квантовых чисел вблизи поворотных точек амплитуда волновой функции максимальна, то есть вероятность найти в них частицу максимальна, как и в классическом рассмотрении. Это работает принцип соответствия.
8.4. Ангармонический осциллятор
В общем случае любая функция, в том числе и потенциальная энергия как функция координаты x, раскладывается в ряд:

Начало отсчёта можно выбрать так, что 


Ограничимся двумя первыми ненулевыми членами ряда:

причём обычно в реальных системах 
Вычислим силу через градиент потенциальной энергии:

По второму закону Ньютона:

Получили дифференциальное уравнение ангармонических колебаний:


Решением этого дифференциального уравнения будет суперпозиция гармонических функций кратных частот (ряд Фурье) с убывающими амплитудами (α
Исключения делают правило знаменитым. Веслав Брудзиньский
ещё >>
Одномерные задачи
Вы будете перенаправлены на Автор24
Свободное движение частицы
Гамильтониан частицы в одномерном, свободном движении (для стационарных состояний) равен:
Тогда уравнение (1) приобретает вид:
где $E_n$ — собственные значения энергии, $\Psi_n$ — собственные функции — решения уравнения (2). Преобразуем уравнение (2) к виду:
где $k^2=\frac<2mE><<\hbar >^2>>0.$ Из уравнения (3) получается, что собственному значению $E$ соответствуют следующие функции:
На волновой вектор $(k)$ ограничений не наложено, следовательно, система имеет непрерывный спектр.
Существуют два состояния, которые отвечают одному значению энергии. Это вырожденные состояния. С кратностью вырождения два. Существование вырождения дает возможность строить бесконечное количество состояний, имеющих одно значение энергии.
Прямоугольная потенциальная яма
Допустим, что потенциальная энергия поля задана:
При этом стационарное уравнение Шредингера для одномерногослучая принимает вид:
Задача состоит в поиске значений энергии ($E$) при которых уравнение (4) имеет ненулевое решение, и соответствующих волновых функций. Разумно допустить, что частица не будет находиться в области потенциала равного бесконечности ($\Psi(\left|x\right|>\frac<2>)\equiv 0$). Исходя вышесказанного предположения уравнение (4) перепишем как:
Общее решение уравнения (5) запишем в виде:
где $k^2=\frac<2mE><<\hbar >^2>$. Использовав условия (6), найдем:
В таком случае для энергии получаем:
где решение при $n=0$ отброшено. Из уравнения (9) следует, что в потенциальной яме с бесконечно высокими стенками, появляется дискретный спектр энергий.
Система собственных функций гамильтониана для частицы в яме имеет вид:
где из условия нормировки получают $A_n=\sqrt<\frac<2>.>$
Готовые работы на аналогичную тему
Гармонический осциллятор
Гармонический осциллятор в квантовой механике определим как частицу имеющую массу $m$ и потенциальную энергию $U=\frac<\varkappa x^2><2>$, где $\varkappa =<\omega >^2m=const.$ Запишем уравнение Шредингера для нашего одномерно случая:
Уравнение (11) имеет конечные, однозначные и гладкие собственные функции при соответствующих собственных значениях $E$, которые равны:
Из уравнения (12) следует, что уровни энергии эквидистантны. Нулевая энергия равна $E_0=\frac<\hbar \omega ><2>$. То, что частица не может лежать на дне потенциальной ямы, связано с принципом неопределенности.
Для квантового осциллятора возможны переходы только между соседними «стационарными» уровнями, при этих переходах квантовое число изменяется на единицу. Это так называемое правило отбора для квантового гармонического осциллятора. При каждом из таких переходов излучается или поглощается фотон, энергия которого равна $\hbar \omega .$ Надо отметить, что говорить, что в стационарных состояниях квантовый осциллятор испытывает колебания с частотой $\omega \ $не верно.
Задание: Какова вероятность найти частицу в левой трети потенциальной ямы, если прямоугольная потенциальная яма имеет ширину $l$ и бесконечно высокие «стенки»? Частица находится в основном состоянии.
Решение:
Состояние частицы, находящейся в прямоугольной яме с бесконечно высокими стенками в основном состоянии (n=1) описывается волновой функцией вида:
Вероятность можно найти как:
Ответ: $P=0,195.$
Задание: Частица находится в бесконечно глубокой потенциальной яме, ширина которой $l$. Состояние частицы описывается волновой функцией вида:
$\Psi\left(x\right)=Ax(x-l)$. Каково распределение вероятностей разных значений энергии $(p\left(E_0\right),\ p\left(E_1\right),\dots $)?
Решение:
Прежде всего, следует нормировать волновую функцию на единицу, вычислить коэффициент A:
Волновая функция имеет вид:
Разложение волновой функции в ряд по собственным функциям $\Psi_n\left(x\right)=\sqrt<\frac<2>
где коэффициенты $C_n$ найдем как:
Вероятность нахождения частицы в квантовом состоянии номер n равна:
Используем результат, полученный в (2.4), имеем:
Ответ: $p\left(E_0\right)\approx 0,999,\ p\left(E_1\right)\approx 0,001$ и т.д.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 12 05 2021
http://davaiknam.ru/text/lekciya-21-4-korpuskulyarno-volnovoj-dualizm-uravnenie-shredin
http://spravochnick.ru/fizika/predmet_i_zadachi_atomnoy_fiziki/odnomernye_zadachi/
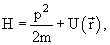
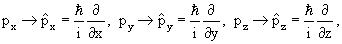
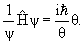
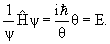
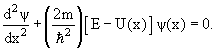
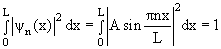
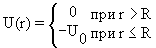
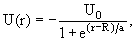




 и частоту
и частоту  ).
). опытах Дж.Томсона исследовалась дифракция электронов на тонкой металлической поликристаллической фольге (рис.21.4). На фотопластинке появлялась дифракционная картина в виде концентрических колец, опять же в соответствии с формулой Брэгга-Вульфа.
опытах Дж.Томсона исследовалась дифракция электронов на тонкой металлической поликристаллической фольге (рис.21.4). На фотопластинке появлялась дифракционная картина в виде концентрических колец, опять же в соответствии с формулой Брэгга-Вульфа.

 и
и  описывают одинаковые состояния частицы.
описывают одинаковые состояния частицы. , или
, или  , …, или
, …, или  , то возможно состояние частицы, описываемое любой линейной комбинацией этих функций:
, то возможно состояние частицы, описываемое любой линейной комбинацией этих функций:





 :
:

 :
:


