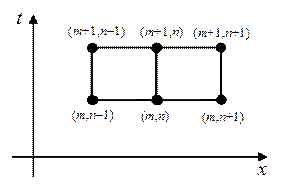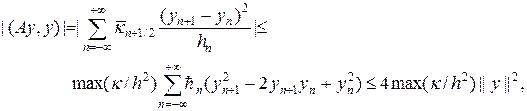Одномерное уравнение теплопроводности численное решение неявная схема

Одномерные уравнения

Лекция №11

Параболические уравнения

Одномерные уравнения

К параболическим уравнениям относятся задачи описания процессов теплопроводности, диффузии, вязкости и ряд других. Типична, например, следующая постановка для линейной теплопроводности в однородной среде:

(1)

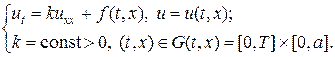
Помимо самого уравнения (1) необходимо определить начальное и граничные условия:

; (2)

. (3)

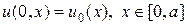
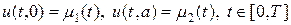
Граничные условия (3) означают, что на левой и правой границе изменения температуры следуют заданным функциональным зависимостям. Эти условия еще называют граничными условиями первого рода. Граничные условия второго рода отвечают заданию на границах потоков тепла, т.е.

. (4)

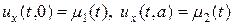
Для граничных условий третьего рода можно записать следующее представление:

. (5)

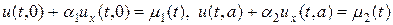
В терминах теплообмена граничные условия третьего рода описывают так называемый линейный (ньютоновский) теплообмен с окружающей средой. Для задачи (1) с начальным (2) и граничными условиями (3) — (5) корректность постановки доказана[1].

Рассмотрим простейшие разностные схемы для численного решения уравнения теплопроводности (1). Выберем в области G(t,x) = [0,T]´[0,a] прямоугольную равномерную сетку с шагами t и h по времени и пространству. В качестве шаблона разностной схемы выберем шеститочечный шаблон, представленный на рис.1. Учитывая шаблон на рис.1, запишем следующую разностную схему

(6)

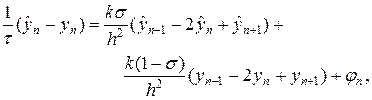
где n = 1,2,…,N-1, s = const. Уравнение (6) необходимо дополнить граничными условиями, например, первого рода:

. (6¢)

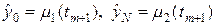
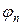
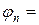
В качестве правой части часто выбирают значение . Параметр s в (6) выступает в качестве свободного параметра, его вариация порождает целое семейство разностных схем от явных до неявных.

Рис.1. Шеститочечный шаблон разностной схемы (6)

Исследуем схему (6), (6¢). Начнем с существования решения и его вычисления. Если s = 0, то схема (6) переходит уже в рассмотренную ранее явную разностную схему (9.26). В этом случае разностное решение легко находится, т.е. его существование и единственность очевидна.

При s ¹ 0 разностная схема (6), (6¢) неявная и ее можно переписать в трехдиагональном форме:

(7)

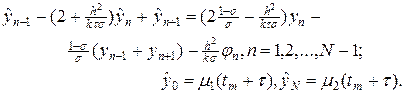
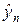
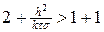
Разностное уравнение на каждом временном слое может быть решено относительно неизвестных методом прогонки. Достаточным условием устойчивости прогонки является условие диагонального преобладания (5.16), которое, согласно (7), выполнено ( ), когда s > 0.

В итоге, решение разностных схем (6), (6¢) существует и единственно при s ³ 0 и при любых ограниченных начальных и краевых условиях. При s = 1 схему называют чисто неявной, а при s = ½ — схемой с полусуммой или симметричной.

Для оценки порядка аппроксимации проведем разложение решений схемы (6) в ряд Тейлора относительно центра разложения (t_m+t / 2,x_n), тогда, опуская довольно утомительные выкладки, можно получить

(8)

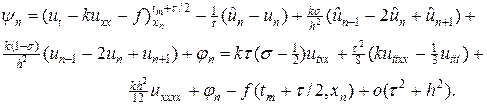
Из (8) видно, что, если положить 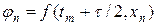, то при s ¹ ½ схема (6) имеет порядок аппроксимации O(t + h 2 ). Для симметричной схемы, у которой s = ½, порядок аппроксимации выше — O(t 2 + h 2 ).

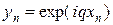
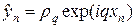
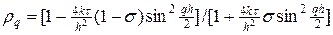
Устойчивость по начальным данным исследуем методом разделения переменных. Поскольку схема (6) линейная, отбросим правую часть и осуществим подстановку и , тогда можно получить множитель роста гармоники

. (9)

Непосредственной проверкой можно убедиться, что множитель роста гармоники (9) меньше единицы при s ³ 0. Проверяя условие , находим

. (10)

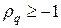
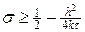
Условие (10) обеспечивает условие равномерной устойчивости схемы (6) по начальным данным в норме 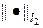. Условие устойчивости по правой части (9.65) выполняется при любых t и h. Таким образом, схема устойчива по начальным данным и по правой части при условии того, что верно неравенство (10).

Для чисто неявной схемы (s = 1), симметричной схемы (s = ½ ) условие (10) выполняется при любых значениях t и h, т.е. эти схемы являются безусловно устойчивыми. Для явной схемы (s = 0) условие (10) выполняется только при условии, что t £ h 2 /(2k), т.е. явная схема является условно устойчивой, что уже было установлено в лекции №9.

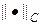
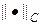
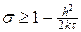
Отметим, что справедливо более сильное утверждение об устойчивости схем (6): они устойчивы в норме . Так из принципа максимума (9.66), (9.67) легко получить достаточное условие устойчивости в норме :

. (10¢)

По сравнению с (10) условие (10¢) более жесткое, но для явной и чисто неявной схем выводы об устойчивости аналогичны тем, которые сделаны выше.

Изучим разностную схему (6), (6¢) на численном примере решения уравнения вида:

(11)

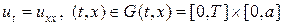
с начальным распределением температуры u₀ в виде равнобедренного треугольника с основанием длиной a и высотой b:

(12)

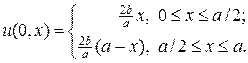
В качестве граничных условий выберем нулевые условия, т.е.

. (13)

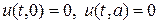
Аналитическое решение задачи (11) — (13) можно представить в виде следующего бесконечного ряда:

. (14)

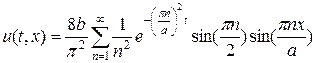
На листинге_№1 приведен код программы численного решения задачи (11) — (13) при различных значениях параметра s. При каждом значении параметра численное решение сравнивалось с аналитическим решением (14) в норме , т.е. находилась ошибка вида: error = .

%Программа решения задачи (11) — (13) при

%различных значениях параметра sigma

%Задаем размеры области интегрирования G=[0,T]x[0,a]

%Определяем размеры сеток по времени и пространству

%Определяем шаги по времени и пространству

%Определяем сетки по времени и пространству

%Находим в узлах сетки значения аналитического

%Рисуем аналитическое решение (14)

%Задаем набор значений параметра sigma, при которых

%будет численно решаться задача (11) — (13) по

%разностной схеме (6), (6′)

%Организуем цикл по времени

%Применяем метод прогонки

%Находим модуль отклонения численного решения от

%аналитического при некотором sigma

%Определяем ошибку численного решения в норме C

%Рисуем 3D график ошибки при sigma=1

%Рисуем 2D график зависимости ошибки численного

%решения от значений параметра sigma

%Функция для вычисления значений аналитического

%решения (14) в точке (t,x)

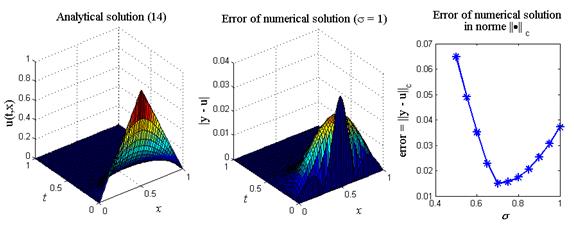
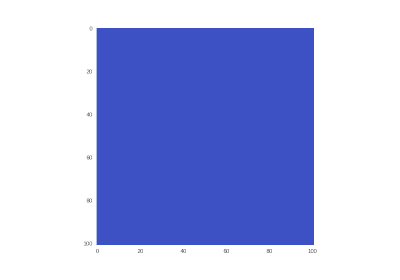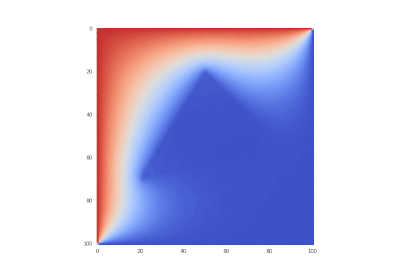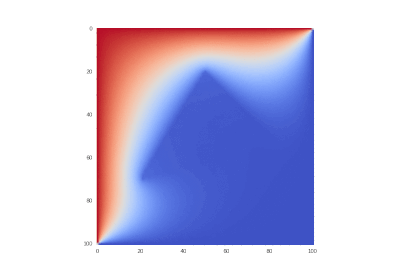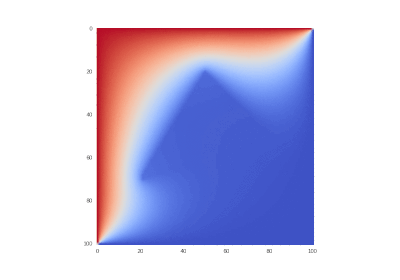
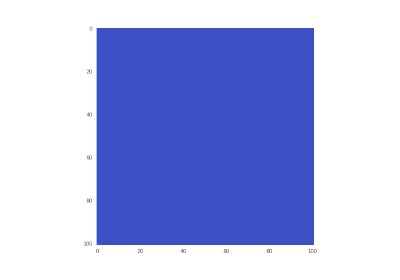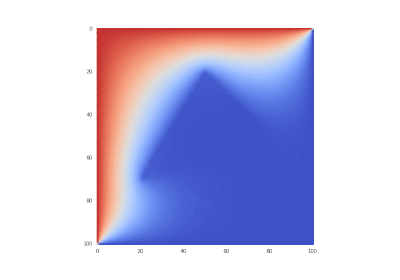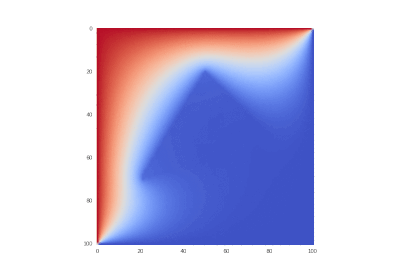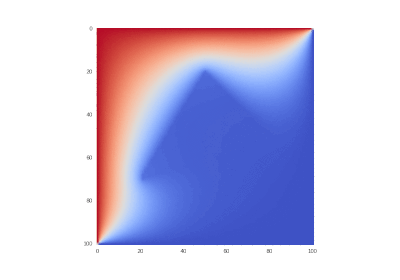
Итог работы кода программы листинга_№1 приведен на рис.2. На левом рисунке приведено 3D изображение аналитического решения (14). На среднем рисунке приведено 3D изображение абсолютного значения ошибки численного решения задачи (11) — (13) с помощью полностью неявной разностной схемы (6), (6¢), т.е. при s = 1. Видно, что пик ошибки приходится на центральный излом в начальном распределении температуры. На рисунке справа приводится ошибка численного решения задачи (11) — (13) в норме 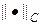в зависимости от значений параметра s (s Î [0,5;1]). Отчетливо виден довольно заметный провал графика в окрестности s = 0,7.

Наилучшая схема. Обобщим разностную схему (6) на случай уравнения теплопроводности с переменным коэффициентом теплопроводности:

. (15)

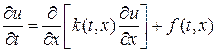
Исследуем общий случай, когда функции k(t,x) и f(t,x) могут быть кусочно-непрерывными. Сильные разрывы могут возникнуть на границе областей, для слоистых сред в случае появления ударных волн и в ряде других приложений. В этом случае решение уравнения (15) следует рассматривать как обобщенное. Обобщенное решение в общем случае не единственно.

Для выделения допустимого решения из множества обобщенных решений необходимо из физических соображений определиться с величинами, которые считаются непрерывными. Для уравнения (15) такими величинами выступают температура u(t,x) и поток тепла W = —k¶u/¶x. Производные этих величин u_x и W_x разрывны в точках разрыва коэффициента теплопроводности и источника тепла соответственно.

Рис.2. Левый рисунок — аналитическое решение (14). Средний и правый
рисунки — решение задачи (11) — (13) с помощью разностной
схемы (6), (6¢) при различных значениях параметра s

Для сходимости к допустимому обобщенному решению составим методом баланса консервативную разностную схему. Для этого перепишем исходное уравнение (15) в явной дивергентной форме, т.е.

. (16)

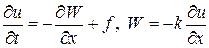
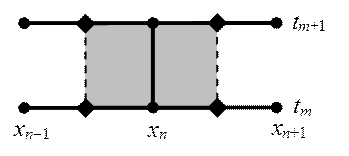
Шаблон и соответствующая ячейка для искомой разностной схемы представлены на рис.3.

Рис.3. Шаблон для разностной схемы уравнения (16)
и ячейка для метода баланса

Запишем для первого уравнения в (16) закон сохранения энергии в виде интеграла по ячейке, заштрихованной на рис.3.

(17)

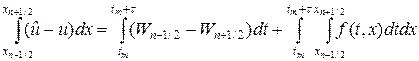
Второе уравнение в (16) проинтегрируем по интервалу сетки [x_n,x_n+1], тогда

. (18)

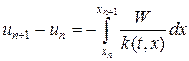
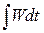
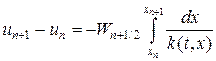
Значения температур припишем узлам сетки, а потоки тепла — серединам интервалов (ромбики на рис.3). Интегралы в (17) аппроксимируем квадратурными формулами. Так, интеграл оценим, исходя из того, что подынтегральное выражение берется с текущего и верхнего слоев. В (18) поток тепла в силу того, что он непрерывен, вынесем из под знака интеграла в средней точке

.

В итоге получим консервативную разностную схему, называемую наилучшей:

, (19)

, (19¢)

,

. (20)

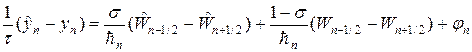
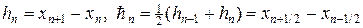
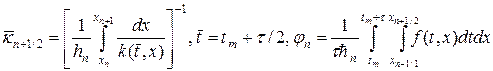
Для аппроксимации интегралов (20) применяют следующий набор формул:

, (21)

, (21¢)

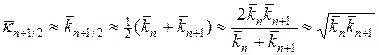
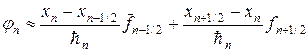
где черта сверху означает отнесение к моменту времени 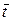. Если разрывы функций k(t,x) и f(t,x) отнесены к узлам сетки, то подстановки в (21) и (21¢) следует понимать, как подстановки односторонних пределов.

Исследуем наилучшую схему (19), (19¢). После подстановки (19¢) в (19) получим обычную трехточечную по пространству схему относительно неизвестных значений 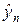на верхнем слое, которая решается методом прогонки. Поскольку имеется диагональное преобладание, т.е. метод прогонки устойчив, постольку может быть получено единственное решение.

Устойчивость по начальным данным разностной схемы (19), (19¢) изучим с помощью метода операторных неравенств. Рассмотрим задачу Коши на всей прямой, считая, что .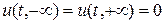

Перепишем схему (19), (19¢) в так называемой канонической операторной форме:

, (22)

где операторы A и B имеют следующий вид:

,

.

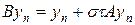
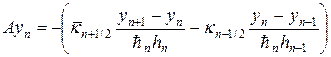
Скалярное произведение определим по формуле:

.

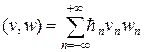
Покажем, что операторы A и B неотрицательные и самосопряженные. Действительно,

.

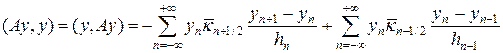
Сдвинем во второй сумме индекс на единицу, тогда

, (23)

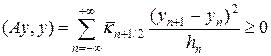
Отметим, что из (23) следует оценка

. (24)

(25)

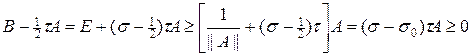
s ³ s₀, 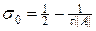. (26)

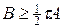
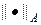
Условие (25) означает, что и по теореме (лекция №9, формулы (9.76) — (9.82)) устойчивости двухслойных разностных схем в канонической форме схема (19) — (20) устойчива в энергетической норме . Таким образом, неравенство (26) является достаточным условием устойчивости схемы (19) — (20).

Учитывая (24), можно получить более сильное достаточное условие устойчивости разностной схемы (19) — (20) в форме:

. (27)

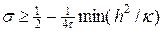
Изучим численно достаточное условие устойчивости (27) на примере использования наилучшей разностной схемы с разрывными функциями, описывающими теплопроводность и правую часть. На листинге_№2 приведен код соответствующей программы.

%Программа тестирования критерия устойчивости (27)

%для наилучшей схемы (19) -(20) численного решения

%Определяем размеры области интегрирования

%Определяем количество узлов в сетках по времени

%вычисляем шаги по времени и пространству

%формируем сетки по времени и пространству

%вычисляем значения коэффициента теплопроводности

%и правой части (источника тепла) в узлах сетки

%рисуем профили коэффициента теплопроводности k(x)

%и источника тепла f(x)

%Находим пороговое значение параметра sigma0 для

%изучения устойчивости наилучшей разностной схемы

%Строим начальное распределение u(0,x)=u0(x)

%температуры в виде треугольного профиля

%Определяем нулевые граничные условия

%Определяем пару значений параметра sigma0 и

%sigma0-eps. При втором значении параметра

%ожидается появление неустойчивости

%Организуем цикл по значением параметра sigma,

%а также по времени и пространству

%определяем левое граничное условие

%Рисуем профили температуры при пороговом значении

%sigma0 и подкритическим значением sigma0-eps

%Определяем функцию коэффициента

if ((x>=0)&(x =(2*a)/3)&(x a/3)&(x =0)&(x =(2*a)/3)&(x a/3)&(x s (s > 0). В лекции №9 аналитически и численно исследовалась бегущая волна для квазилинейного уравнения теплопроводности без источника тепла. И, наконец, в той же лекции аналитически и численно изучалось квазилинейное уравнение теплопроводности с источником тепла, степенным образом, зависящим от температуры, т.е. при f

u s +1 . Во всех трех случаях использовалась чисто неявная схема с весом s = 1. Запишем ее в следующем виде:

. (29)

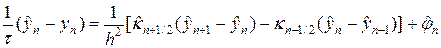
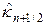
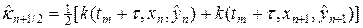
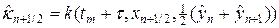
В (29) под понимаются выражения типа (21), т.е.

(30)

. (30¢)

Аналогично (30), (30¢) можно аппроксимировать в (29) источник тепла .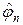

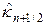
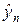
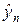
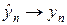
Можно показать, что схема (29) абсолютно устойчива и консервативна и на четырежды непрерывно дифференцируемых решениях имеет погрешность аппроксимации O(t + h 2 ). Вследствие зависимости от неизвестного решения на следующем слое алгебраическая схема (29) является нелинейной относительно . Понятно, что, когда t ® 0 — , т.е. при достаточно малом t существует вещественное решение системы (29). Понятно также, что при большом значении t вещественное решение может отсутствовать.

Решать алгебраическую систему уравнений можно несколькими способами. Рассмотрим подробно метод последовательных приближений, в котором и берутся с предыдущей итерации, т.е.

, (31)

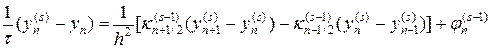
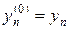
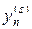
где индекс s = 1,2,… описывает номера итераций. В (31) в качестве нулевого приближения берутся решения с предыдущего слоя, т.е. . Величины находятся из (31) методом прогонкой. Итерации в (31) сходятся линейно и обычно не быстро. Итерации могут и расходиться. В этом случае расчет можно вести с фиксированным числом итераций (обычно 2, 3 итерации).

В качестве критерия сходимости итераций можно использовать условие

(32)

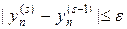
или более жесткое условие

, (32¢)

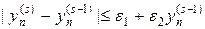
где e, e₁, e₂ — некоторые малые неотрицательные числа. Критерий сходимости (32) либо (32¢) должен выполняться для всех узлов сетки n. Если за разумное число итераций критерий сходимости не выполняется необходимо уменьшить шаг по времени и повторить процедуру повторно. После выполнения одного из критериев (32), (32¢) полагают 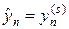и цикл перехода на следующий слой завершается.

Рассмотрим пример численного решения квазилинейного уравнения теплопроводности с источником, в котором коэффициент теплопроводности и источник тепла степенным образом зависят от температуры. Запишем это уравнение в виде

, (33)

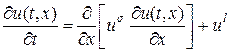
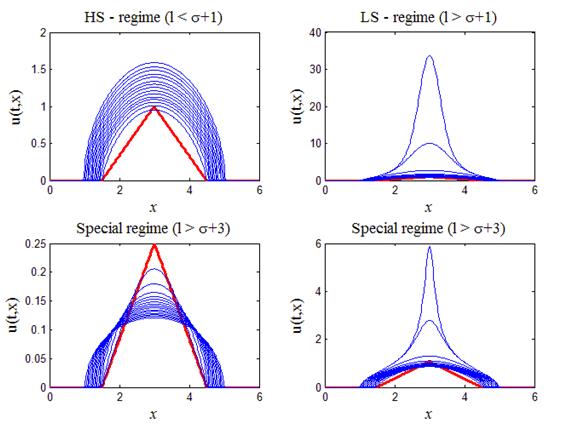
В лекции №9 уже рассмотрено аналогичное уравнение (9.18), точнее рассмотрено аналитическое решение (9.19) — (9.21) этого уравнения при l = s + 1. Продолжим изучение уравнения (33) численным методом в еще трех случаях[2]: 1) так называемый HS-режим, когда l s + 1; 3) особый случай, когда l > s + 3. Третий случай интересен тем, что в зависимости от начального распределения температуры, последующая эволюция решения может пойти по двум прямо противоположным направлениям. Если амплитуда начального распределения ниже некоторого порогового значения, то в дальнейшем тепло будет “расползаться” по пространству неограниченно и амплитуда решения будет стремиться к нулю. Если амплитуда начального распределения температуры является надпороговой, то дальнейшее изменение решения происходит в режиме с обострением, т.е. за конечное время решение обращается в бесконечность.

%Программа решения квазилинейного уравнения

%теплопроводности с источником (33) с помощью

%разностной схемы (31)

%Очищаем рабочее пространство

%Определяем число шагов по времени и

%максимальное количество итераций на

%Определяем диапазон изменения переменной x и

%число узлов сетки на отрезке [0,a]

%Определяем шаг и сетку по пространству

%Определяем степень температурной зависимости

%Определяем четыре расчета:1)HS-режим, когда

%1 sigma+1; 3)режим

%l>sigma+3 с двумя типами начальных данных:

%подпороговый пик возмущения и надпороговый

l=[sigma sigma+2 sigma+4 sigma+4];

%Вариация высоты пика начального возмущения

%для четырех расчетов

%Основной цикл для четырех расчетов

%Начальное распределение температуры в

%виде равнобедренного треугольника с

%высотой b(k) и основанием длиной 0.5*a

if (x(n)>=0.25*a)&(x(n) =0.5*a)*(x(n) s + 3 в зависимости от амплитуды начального распределения возможны два прямо противоположных режима динамики. На левом нижнем рисунке, при подпороговой начальной амплитуде тепло “расползается” неограниченно по пространству, амплитуда распределения стремится к нулю, при этом источник тепла не перестает действовать. На правом нижнем рисунке, при надпороговой начальной амплитуде температура в центре в начале падает, а потом начинает расти неограниченно в режиме с обострением, причем полуширина пика, как и LS-режиме, стремится к нулю. На всех четырех рисунках жирной (красной) линией выделен начальный температурный профиль.

Рис.5. Различные типы динамики решений уравнения (33) в
зависимости от соотношения параметров s и l

Уравнение теплопроводности

Ранее (см. разд. 2.1.2, 2.1.3) уже были построены и исследованы разностные схемы решения смешанной задачи для одномерного уравнения теплопроводности:

(2.75)

Были получены две двухслойные схемы — явная (2.3) и неявная (2.4). В явной схеме значения сеточной функции на верхнем (j + 1)-ом слое вычисляли с помощью решения на нижнем слое [соотношение (2.13)]. Для нахождения решения на (j + 1)-м слое по неявной схеме была получена трехдиагональная система линейных алгебраических уравнений (2.22), которую решают методом прогонки.

Неявная схема безусловно устойчива, явная схема устойчива при выполнении условия

Обе схемы сходятся к решению исходной задачи со скоростью .

Схемы (2.3), (2.4) построены для случая, когда значения искомой функции (температуры) Uна границах х = 0, х = 1определяются заданными функциями . Однако граничные условия в смешанной задаче (2.75) могут быть и иными, в них может входить производная искомой функции. Например, если конец стержня х=0 теплоизолирован, то условие имеет вид

В этом случае, как и при решении волнового уравнения, данное условие нужно записывать в схемах (2.3), (2.4) в разностном виде.

Перейдем теперь к построению разностных схем для уравнения теплопроводности с двумя пространственными переменными. Примем для простоты а = 1. Тогда это уравнение можно записать в виде

(2.76)

Пусть при t=0 начальное условие задано в виде

(2.77)

В отличие от волнового уравнения, требующего два начальных условия, в уравнение теплопроводности входит только первая производная по t, и необходимо задавать одно начальное условие.

Часто задачи теплопроводности или диффузии, описываемые двумерным уравнением (2.76), решаются в ограниченной области. Тогда, кроме начального условия (2.77), нужно формулировать граничные условия. В частности, если расчетная область представляет прямоугольный параллелепипед (рис. 2.24), то нужно задавать граничные условия на его боковых гранях. Начальное условие (2.77) задано на нижнем основании параллелепипеда.

Рис. 2.24. Расчетная область

Введем простейшую сетку с ячейками в виде прямоугольных параллелепипедов, для чего проведем три семейства плоскостей: хi= ih1(i=0,1. I), (j=0,1. J), . Значение сеточной функции в узлах обозначим символом . С помощью этих значений можно построить разностные схемы для уравнения (2.76).

Рассмотренные выше схемы для одномерного уравнения легко обобщаются на двумерный случай.

Построим явную разностную схему, шаблон которой изображен на рис. 2.25. Аппроксимируя производные отношениями конечных разностей, получаем следующее сеточное уравнение:

Рис. 2.25. Шаблон двумерной схемы

Отсюда можно найти явное выражение для значения сеточной функции на (k + 1)-ом слое:

(2.78)

Условие устойчивости имеет вид

(2.79)

При получается особенно простой вид схемы (2.78):

(2.80)

Полученная схема сходится со скоростью

Формулы (2.78) или (2.80) представляют собой рекуррентные соотношения для последовательного вычисления сеточной функции во внутренних узлах слоев k = 1,2. К. На нулевом слое используется начальное условие (2.77), которое записывается в виде

(2.81)

Значения в граничных узлах вычисляют с помощью граничных условий.

Алгоритм решения смешанной задачи для двумерного уравнения теплопроводности изображен на рис. 2.26. Здесь решение хранится на двух слоях: нижнем (массив ) и верхнем (массив ). Блоки граничных условий необходимо сформировать в зависимости от конкретного вида этих условий. Результаты выводят на каждом слое, хотя можно ввести шаг выдачи (см. рис. 2.13).

Рис. 2.26. Алгоритм решения двумерного уравнения теплопроводности

Построим теперь абсолютно устойчивую неявную схему для решения уравнения (2.76), аналогичную схеме (2.4) для одномерного уравнения теплопроводности. Аппроксимируя в (2.76) вторые производные по пространственным переменным на (k + 1)-ом слое, получаем следующее разностное уравнение:

(2.82)

Это уравнение можно записать в виде системы линейных алгебраических уравнений относительно значений сеточной функции на каждом слое:

(2.83)

К этой системе уравнений нужно добавить граничные условия для определения значений сеточной функции в граничных узлах (т.е. при i= 0, I; j = 0, J). На нулевом слое решение находится из начального условия (2.77), представленного в виде (2.81).

Система (2.83), полученная для двумерного уравнения теплопроводности, имеет более сложный вид, чем аналогичная система (2.22) для одномерного случая, которую можно решить методом прогонки. Таким образом, распространение неявной схемы на многомерный случай приводит к значительному усложнению вычислительного алгоритма и увеличению объема вычислений.

Недостатком явной схемы (2.78) является жесткое ограничение на шаг по времени τ, вытекающее из условия (2.79). Существуют абсолютно устойчивые экономичные разностные схемы, позволяющие вести расчет со сравнительно большим значением шага по времени и требующие меньшего объема вычислений. Две из них будут рассмотрены в разд. 2.3.3.

Уравнение теплопроводности в tensorflow

Привет, Хабр! Некоторое время назад увлекся глубоким обучением и стал потихоньку изучать tensorflow. Пока копался в tensorflow вспомнил про свою курсовую по параллельному программированию, которую делал в том году на 4 курсе университета. Задание там формулировалось так:

Линейная начально-краевая задача для двумерного уравнения теплопроводности:

Хотя правильнее было бы назвать это уравнением диффузии.

Задачу тогда требовалось решить методом конечных разностей по неявной схеме, используя MPI для распараллеливания и метод сопряженных градиентов.

Я не специалист в численных методах, пока не специалист в tensorflow, но опыт у меня уже появился. И я загорелся желанием попробовать вычислять урматы на фреймворке для глубокого обучения. Метод сопряженных градиентов реализовывать второй раз уже не интересно, зато интересно посмотреть как с вычислением справится tensorflow и какие сложности при этом возникнут. Этот пост про то, что из этого вышло.

Численный алгоритм

Разностная схема:

Чтобы проще было расписывать, введем операторы:

Явная разностная схема:

В случае явной разностной схемы для вычисления используются значения функции в предыдущий момент времени и не требуется решать уравнение на значения . Однако такая схема менее точная и требует значительно меньший шаг по времени.

Неявная разностная схема:

Перенесем в левую сторону все связанное с , а в правую и домножим на :

По сути мы получили операторное уравнение над сеткой:

что, если записать значения в узлах сетки как обычный вектор, является обычной системой линейных уравнений (). Значения в предыдущий момент времени константы, так как уже рассчитаны.
Для удобства представим оператор как разность двух операторов:

Заменив на нашу оценку , запишем функционал ошибки:

где — ошибка в узлах сетки.

Будем итерационно минимизировать функционал ошибки, используя градиент.

В итоге задача свелась к перемножению тензоров и градиентному спуску, а это именно то, для чего tensorflow и был задуман.

Реализация на tensorflow

Кратко о tensorflow

В tensorflow сначала строится граф вычислений. Ресурсы под граф выделяются внутри tf.Session. Узлы графа — это операции над данными. Ячейками для входных данных в граф служат tf.placeholder. Чтобы выполнить граф, надо у объекта сессии запустить метод run, передав в него интересующую операцию и входные данные для плейсхолдеров. Метод run вернет результат выполнения операции, а также может изменить значения внутри tf.Variable в рамках сессии.

tensorflow сам умеет строить графы операций, реализующие backpropagation градиента, при условии, что в оригинальном графе присутствуют только операции, для которых реализован градиент (пока не у всех).

Сначала код инициализации. Здесь производим все предварительные операции и считаем все, что можно посчитать заранее.

По-хорошему надо было считать значения функции на краях заданными и оптимизировать значения функции только во внутренней области, но с этим возникли проблемы. Способа сделать оптимизируемым только часть тензора не нашлось, и у операции присвоения значения срезу тензора не написан градиент (на момент написания поста). Можно было бы попробовать хитро повозиться на краях или написать свой оптимизатор. Но и просто добавление разности на краях значений функции и краевых условий в функционал ошибки хорошо работает.

Стоит отметить, что метод с адаптивным моментом показал себя наилучшим образом, пусть функционал ошибки и квадратичный.

Вычисление функции: в каждый момент времени делаем несколько оптимизационных итераций, пока не превысим maxiter или ошибка не станет меньше eps, сохраняем и переходим к следующему моменту.

Запуск:

Результаты

Условие как и оригинальное, но без в уравнении:

Что легко правится в коде:

Разницы почти нет, потому что производные имеют большие порядки, чем сама функция.

Условие с одним нагревающимся краем:

Условие с остыванием изначально нагретой области:

Условие с включением нагрева в области:

Рисование гифок

Функция рисования 3D-гифки:

В основной класс добавляем метод, возвращающий U в виде pandas.DataFrame

Функция рисования 2D-гифки:

Стоит отметить, что оригинальное условие без использования GPU считалось 4м 26с, а с использованием GPU 2м 11с. При больших значениях точек разрыв растет. Однако не все операции в полученном графе GPU-совместимы.

• Intel Core i7 6700HQ 2600 МГц,
• NVIDIA GeForce GTX 960M.

Посмотреть, какие операции на чем выполняются, можно с помощью следующего кода:

Это был интересный опыт. Tensorflow неплохо показал себя для этой задачи. Может быть даже такой подход получит какое-то применение — всяко приятнее писать код на питоне, чем на C/C++, а с развитием tensorflow станет еще проще.