Одномерное волновое уравнение относится к
Волновое уравнение
Wave equation
Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением
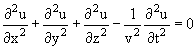 | (1) |
где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид
u(x,t) = Asin(ωt − xv).
Длина волны λ − путь, пройденный возмущением (состоянием с определённой фазой) за время равное периоду колебаний T
Частота ω и период колебаний T связаны соотношением
Эквивалентные формулы для монохроматической волны, распространяющейся вдоль оси x
u(x,t) = Asin(ωt − kx) = Asinω(t − x/v) = Asin2π(t/T − x/λ).
u(r,t) = (A/r)sin(ωt − kr).
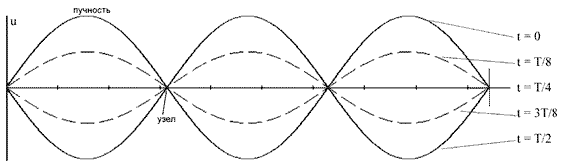
Стоячая волна. При наложении монохроматических волн одинаковой частоты образуется устойчивая картина результирующих колебаний с характерными максимумами и минимумами.
Стоячая волна образуется в системах с двумя жёстко закреплёнными точками. При отражении фаза волны меняется на π и происходит интерференция падающей и отраженной волн.
| Падающая волна | u1 = Asin(ωt + kx) | |
| Отражённая волна | u2 = Asin(ωt − kx + π) | |
| Стоячая волна | u1 + u2 = A(x)cosωt | (2) |
Соотношение (2) можно получить, используя формулу
sinα − sinβ = 2sin[(α − β)/2] cos[(α + β)/2]
и положив 2Asin(2πx/λ) = A(x), A(x) − амплитуда стоячей волны.
Одномерные волны: математическое выражение и примеры
Одномерные волны: математическое выражение и примеры — Наука
Содержание:
В одномерные волны Это те, которые распространяются в одном направлении, независимо от того, происходит ли вибрация в том же направлении распространения или нет. Хорошим примером этого является волна, которая проходит через тугую струну, как у гитары.
В плоской волнепересекать, частицы колеблются в вертикальном направлении (они движутся вверх и вниз, см. красную стрелку на рисунке 1), но это одномерно, поскольку возмущение распространяется только в одном направлении, следуя желтой стрелке.
Одномерные волны в повседневной жизни возникают довольно часто. В следующем разделе описаны некоторые их примеры, а также не одномерные волны, чтобы четко установить различия.
Примеры одномерных волн и неодномерных волн
Одномерные волны
Вот несколько примеров одномерных волн, которые можно легко наблюдать:
— Звуковой импульс, который проходит через прямую полосу, поскольку это возмущение, которое распространяется по всей длине полосы.
— Волна, которая проходит через канал с водой, даже если водная поверхность перемещается не параллельно каналу.
— Волны, распространяющиеся по поверхности или в трехмерном пространстве, также могут быть одномерными, если их волновые фронты параллельны друг другу и распространяются только в одном направлении.
Неодномерные волны
Пример неодномерной волны можно найти в волнах, которые образуются на поверхности неподвижной воды, когда падает камень. Это двумерная волна с цилиндрическим волновым фронтом.
Другой пример неодномерной волны — звуковая волна, которую фейерверк генерирует, взрываясь на определенной высоте. Это трехмерная волна со сферическими волновыми фронтами.
Математическое выражение одномерной волны.
Самый общий способ выразить одномерную волну, которая распространяется без затухания в положительном направлении оси. Икс и со скоростью v математически:
В этом выражении Y представляет нарушение положения Икс Мгновенно т. Форма волны задается функцией F. Например, волновая функция, показанная на рисунке 1: y (x, t) = cos (x — v t) а волновой образ соответствует моменту t = 0.
Такая волна, описываемая функцией косинуса или синуса, называется гармоническая волна. Хотя это не единственная существующая форма волны, она чрезвычайно важна, потому что любая другая волна может быть представлена как суперпозиция или сумма гармонических волн. Речь идет об известном Теорема Фурье, поэтому используется для описания сигналов всех видов.
Когда волна движется в отрицательном направлении оси x, она просто меняет v от -v в аргументе, оставив:
у (х, t) = g (х + v t)
На рисунке 3 показана анимация волны, бегущей влево: это форма, называемая функцией.Лоренциана и она математическое выражение:
В этом примере скорость распространения равна v = 1, -Единица пространства для каждой единицы времени-.
Одномерное волновое уравнение
Волновое уравнение — это уравнение в частных производных, решением которого, конечно же, является волна. Он устанавливает математические отношения между пространственной и временной частью и имеет вид:
Пример работы
Ниже приводится общее выражение y (x, t) для гармонической волны:
а) Опишите физический смысл параметров А, к, ω Y θo.
б) Какое значение имеют знаки ± в аргументе косинуса?
c) Убедитесь, что данное выражение действительно является решением волнового уравнения из предыдущего раздела, и найдите скорость v распространения.
Решение для)
Характеристики волны находятся в следующих параметрах:
-ТО представляет амплитуда или «высота волны».
-k находится в волновое число и связана с длиной волны λ через к = 2π / λ.
-ω это fугловая частота и связан с периодТ колебание волны
-θo это Начальная стадия, который связан с начальной точкой волны.
Решение б)
Отрицательный знак принимается, если волна распространяется в положительном направлении оси X, и положительный знак в противном случае.
Решение c)
Проверить, что данное выражение является решением волнового уравнения, просто: берется частная производная функции у (х, т) дважды по x, дважды повторно получить частично по t, а затем объединить оба результата, чтобы получить равенство:
Эти результаты подставляются в волновое уравнение:
Так много К поскольку косинус упрощен, так как они появляются по обе стороны от равенства, а аргумент косинуса тот же, поэтому выражение сводится к:
-k 2 = (1 / v 2 ) (-ω 2 )
Что позволяет получить уравнение для v с точки зрения ω Y k:
Ссылки
- Электронное обучение. Уравнение одномерных гармонических волн. Получено с: e-ducativa.catedu.es
- Уголок физики. Волновые классы. Получено с: fisicaparatontos.blogspot.com.
- Фигероа, Д. 2006. Волны и квантовая физика. Серия: Физика для науки и техники. Отредактировал Дуглас Фигероа. Университет Симона Боливара. Каракас Венесуэла.
- Лаборатория физики Волновое движение. Получено с: fisicalab.com.
- Пирс, А. Лекция 21: Одномерное волновое уравнение: решение Д’Аламбера. Получено с: ubc.ca.
- Волновое уравнение. Получено с: en.wikipedia.com
Что такое детрит? (В биологии, геологии и медицине)
На каком континенте самая большая концентрация населения?
Волновое уравнение
Одним из наиболее распространенных в инженерной практике уравнений с частными производными второго порядка является волновое уравнение, описывающее различные виды колебаний. Поскольку колебания — процесс нестационарный, то одной из независимых переменных является время t. Кроме того, независимыми переменными в уравнении являются также пространственные координаты х, у, z. В зависимости от их количества различают одномерное, двумерное и трехмерное волновые уравнения.
Одномерное волновое уравнение – уравнение, описывающее продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения, а также поперечные колебания тонкого стержня (струны) и другие задачи. Двумерное волновое уравнение используют для исследования колебаний тонкой пластины (мембраны). Трехмерное волновое уравнениеописывает распространение волн в пространстве (например, звуковых волн в жидкости, упругих волн в сплошной среде и т.п.).
Рассмотрим одномерное волновое уравнение, которое можно записать в виде

Для поперечных колебаний струны искомая функция U(x,t) описывает положение струны в момент t. В этом случае а2 = Т/ρ, где Т — натяжение струны, ρ — ее линейная (погонная) плотность. Колебания предполагаются малыми, т.е. амплитуда мала по сравнению с длиной струны. Кроме того, уравнение (2.63) записано для случая свободных колебаний. В случае вынужденных колебаний в правой части уравнения добавляют некоторую функцию f(x,t), характеризующую внешние воздействия, при этом сопротивление среды колебательному процессу не учитывается.
Простейшей задачей для уравнения (2.63) является задача Коши: в начальный момент времени задаются два условия (количество условий равно порядку входящей в уравнение производной по t):

Эти условия описывают начальную форму струны 

На практике чаще приходится решать не задачу Коши для бесконечной струны, а смешанную задачу для ограниченной струны некоторой длины l. В этом случае задают граничные условия на ее концах. В частности, при закрепленных концах их смещения равны нулю, и граничные условия имеют вид

Рассмотрим некоторые разностные схемы для решения задачи (2.63)-(2.65). Простейшей является явная трехслойная схема типа крест (шаблон показан на рис. 2.21). Заменим в уравнении (2.63) вторые производные искомой функции Uпо tи х их конечно-разностными соотношениями с помощью значений сеточной функции 

Рис. 2.21. Шаблон явной схемы
Отсюда можно найти явное выражение для значения сеточной функции на ( j + 1)-ом слое:

Здесь, как обычно в трехслойных схемах, для определения неизвестных значений на (j + 1)-ом слое нужно знать решения на j-ом и (j — 1)-ом слоях. Поэтому начать счет по формулам (2.66) можно лишь для второго слоя, а решения на нулевом и первом слоях должны быть известны. Их находят с помощью начальных условий (2.64). На нулевом слое имеем

Для получения решения на первом слое воспользуемся вторым начальным условием (2.64). Производную 

Из этого соотношения можно найти значения сеточной функции на первом временном слое:

Отметим, что аппроксимация начального условия в виде (2.68) ухудшает аппроксимацию исходной дифференциальной задачи: погрешность аппроксимации становится порядка 

Вместо 

Тогда (2.70) примет вид:

Разностная схема (2.66) с учетом (2.71) обладает погрешностью аппроксимации порядка
При решении смешанной задачи с граничными условиями вида (2.65), т.е. когда на концах рассматриваемого отрезка заданы значения самой функции, второй порядок аппроксимации сохраняется. В этом случае для удобства крайние узлы сетки располагают в граничных точках (х0=0, xI = l). Однако граничные условия могут задаваться и для производной.
Например, в случае свободных продольных колебаний стержня на его незакрепленном конце задается условие

Если это условие записать в разностном виде с первым порядком аппроксимации, то погрешность аппроксимации схемы станет порядка 
Рассмотренная разностная схема (2.66) решения задачи (2.63) — (2.65) условно устойчива. Необходимое и достаточное условие устойчивости:

Следовательно, при выполнении этого условия и с учетом аппроксимации схема (2.66) сходится к исходной задаче со скоростью O(h2+τ2). Данная схема часто используется в практи-ческих расчетах. Она обеспечивает приемлемую точность получения решения U(x,t), которое имеет непрерывные производные четвертого порядка.
Рис. 2.22. Алгоритм решения волнового уравнения
Алгоритм решения задачи (2.63)-(2.65) с помощью данной явной разностной схемы приведен на рис. 2.22. Здесь представлен простейший вариант, когда все значения сеточной функции, образующие двумерный массив, по мере вычисления хранятся в памяти компьютера, а после решения задачи выводятся результаты. Можно было бы предусмотреть хранение решения лишь на трех слоях, что сэкономило бы память. Результаты в таком случае можно выводить в процессе счета (см. рис. 2.13).
Существуют и другие разностные схемы решения волнового уравнения. В частности, иногда удобнее использовать неявные схемы, чтобы избавиться от ограничений на величину шага, налагаемых условием (2.73). Эти схемы обычно абсолютно устойчивы, однако алгоритм решения задачи и программа для компьютера усложняются.
Построим простейшую неявную схему. Вторую производную по tв уравнении (2.63) аппроксимируем, как и ранее, по трехточечному шаблону с помощью значений сеточной функции на слоях j— 1, j, j + 1. Производную до х заменяем полусуммой ее аппроксимации на (j + 1)-ом и (j— 1)-ом слоях (рис. 2.23):
Рис. 2.23. Шаблон неявной схемы
Из этого соотношения можно получить систему уравнений относительно неизвестных значений сеточной функции на (j+ 1)-ом слое:

Полученная неявная схема устойчива и сходится со скоростью 
При двух или трех независимых пространственных переменных волновые уравнения принимают вид
Для них также могут быть построены разностные схемы по аналогии с одномерным волновым уравнением. Разница состоит в том, что нужно аппроксимировать производные по двум или трем пространственным переменным, что, естественно, усложняет алгоритм и требует значительно больших объемов памяти и времени счета. Подробнее двумерные задачи будут рассмотрены ниже для уравнения теплопроводности.
http://ru1.warbletoncouncil.org/ondas-unidimensionales-2624
http://3ys.ru/metody-resheniya-differentsialnykh-uravnenij/volnovoe-uravnenie.html