Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть.
Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.
Для начала стоит вспомнить, что такое однородные системы линейных алгебраических уравнений. В теме «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи» вопрос классификации систем осуществлялся подробно, здесь же лишь вкратце напомню основные термины. Итак, система линейных алгебраических уравнений (СЛАУ) называется однородной, если все свободные члены этой системы равны нулю. Например, система $\left \ < \begin
Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, $x_1=0$, $x_2=0$, $x_3=0$ и $x_4=0$ в записанную выше систему. Получим два верных равенства:
Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). Возникает первый вопрос: как выяснить, сколько решений имеет заданная нам однородная СЛАУ? Одно (нулевое) или бесконечность?
Та однородная СЛАУ, которая рассмотрена выше, имеет не только нулевое решение. Подставим, например, $x_1=1$, $x_2=-1$, $x_3=2$ и $x_4=3$:
Мы получили два верных равенства, поэтому $x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$ – тоже является решением данной СЛАУ. Отсюда, кстати, следует вывод: так как наша СЛАУ имеет более чем одно решение, то эта СЛАУ является неопределенной, т.е. она имеет бесконечное количество решений.
Кстати сказать, чтобы не писать каждый раз выражения вроде «$x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$», пишут все значения переменных в матрицу-столбец: $\left(\begin
Теперь можно вернуться к вопросу о количестве решений однородной СЛАУ. Согласно следствию из теоремы Кронекера-Капелли, если $r=n$ ($n$ – количество переменных), то СЛАУ имеет единственное решение. Если же $r < n$, то СЛАУ имеет бесконечное количество решений.
Случай $r=n$ не интересен. Для однородных СЛАУ он означает, что система имеет только нулевое решение. А вот случай $r < n$ представляет особый интерес.
Этот случай уже был рассмотрен в теме «Базисные и свободные переменные. Общее и базисное решения СЛАУ». По сути, однородные СЛАУ – это всего лишь частный случай системы линейных уравнений, поэтому вся терминология (базисные, свободные переменные и т.д.) остаётся в силе.
Что такое базисные и свободные переменные? показать\скрыть
Прежде чем дать определение этим терминам, стоит вспомнить, что означает фраза «ранг матрицы равен $r$». Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют. Теперь можно дать следующее определение:
Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.
Фундаментальная система решений однородной СЛАУ.
С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен $r$, то такая СЛАУ имеет $n-r$ линейно независимых решений: $\varphi_1$, $\varphi_2$. $\varphi_
Часто вместо словосочетания «фундаментальная система решений» используют аббревиатуру «ФСР». Если решения $\varphi_1$, $\varphi_2$. $\varphi_
$$ X=C_1\cdot \varphi_1+C_2\cdot \varphi_2+\ldots+C_
где $C_1$, $C_2$. $C_
Что значит «линейно независимые решения»? показать\скрыть
В данной ситуации под решением понимается матрица-столбец, в которой перечислены значения неизвестных.
Решения $\varphi_1$, $\varphi_2$, $\ldots$, $\varphi_n$ называются линейно зависимыми, если существуют такие константы $\alpha_1,\;\alpha_2,\;\alpha_3,\ldots,\alpha_n$, что выполняется следующее равенство:
$$ \alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2+\ldots+\alpha_n\cdot \varphi_n=O $$
при условии, что среди коэффициентов $\alpha_i$ есть хотя бы один, не равный нулю.
Если же указанное выше равенство возможно лишь при условии $\alpha_1=\alpha_2=\ldots=\alpha_n=0$, то система решений называется линейно независимой.
Буква «$O$» в данном определении обозначает нулевую матрицу. Проще всего пояснить это определение на конкретном примере. Давайте рассмотрим ту СЛАУ, о которой шла речь в начале темы. Мы уже проверили, что $\varphi_1=\left(\begin
Примем $\alpha_1=-1$, $\alpha_2=0$, $\alpha_3=4$, $\alpha_4=3$. Выясним, чему же равно выражение $\alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2+\alpha_3\cdot \varphi_3+\alpha_4\cdot \varphi_4$:
$$ \alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2+\alpha_3\cdot \varphi_3+\alpha_4\cdot \varphi_4= -1\cdot \left(\begin
Итак, существуют такие значения констант $\alpha_1$, $\alpha_2$, $\alpha_3$, $\alpha_4$, не все одновременно равные нулю, что выполняется равенство $\alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2+\alpha_3\cdot \varphi_3+\alpha_4\cdot \varphi_4=O$. Вывод: совокупность решений $\varphi_1$, $\varphi_2$, $\varphi_3$, $\varphi_4$ – линейно зависима.
Для сравнения: равенство $\alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2=O$ возможно лишь при условии $\alpha_1=\alpha_2=0$ (я не буду это доказывать, поверьте на слово 🙂 ). Следовательно, система $\varphi_1$, $\varphi_2$ является линейно независимой.
Если система является неопределённой, указать фундаментальную систему решений.
Итак, мы имеем однородную СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая однородная система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$ \left( \begin
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.
И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $\rang A=\rang\widetilde = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:
На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $\left( \begin
Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:
$$ M_<2>^<(1)>=\left| \begin
Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.
Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №2 и №4:
$$ M_<2>^<(2)>=\left| \begin
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №2 (он соответствует переменной $x_2$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_2$ и $x_4$ можно принять в качестве базисных.
Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.
Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_
В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.
Базисные переменные выбраны: это $x_1$ и $x_3$. Количество свободных переменных, как и количество решений в ФСР, равно $n-r=2$. Свободными переменными будут $x_2$ и $x_4$. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $\left( \begin
$$ \left( \begin
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:
Почему меняются знаки? Что вообще значит это перенесение столбцов? показать\скрыть
Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $\left( \begin
Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$ \left( \begin
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Вспоминая, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, получим:
Нами найдено общее решение заданной однородной СЛАУ. Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=2x_2-\frac<1><3>x_4$ и $x_3=-\frac<4><3>x_4$ в левую часть первого уравнения, получим:
$$ 3x_1-6x_2+9x_3+13x_4=3\cdot \left(2x_2-\frac<1><3>x_4\right)-6x_2+9\cdot \left(-\frac<4><3>x_4\right)+13x_4=0. $$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Теперь найдем фундаментальную систему решений. ФСР будет содержать $n-r=2$ решения. Для нахождения ФСР составим таблицу. В первой строке таблицы будут перечислены переменные: сначала базисные $x_1$, $x_3$, а затем свободные $x_2$ и $x_4$. Всего в таблице будут три строки. Так как у нас 2 свободные переменные, то под свободными переменными запишем единичную матрицу второго порядка, т.е. $\left(\begin
Теперь будем заполнять свободные ячейки. Начнём со второй строки. Мы знаем, что $x_1=2x_2-\frac<1><3>x_4$ и $x_3=-\frac<4><3>x_4$. Если $x_2=1$, $x_4=0$, то:
Найденные значения $x_1=2$ и $x_3=0$ запишем в соответствующие пустые ячейки второй строки:
Заполним и третью строку. Если $x_2=0$, $x_4=1$, то:
Найденные значения $x_1=-\frac<1><3>$ и $x_3=-\frac<4><3>$ запишем в соответствующие пустые ячейки третьей строки. Таким образом таблица будет заполнена полностью:
Из второй и третьей строки таблицы мы и запишем ФСР. Матрица неизвестных для нашей системы такова: $X=\left(\begin
$$ \varphi_1=\left(\begin
Совокупность $\varphi_1=\left(\begin
$$ X=C_1\cdot\left(\begin
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Общее решение: $\left\ <\begin
Записать ФСР однородной СЛАУ
зная общее решение. Записать общее решение с помощью ФСР.
Общее решение уже было получено в теме «метод Крамера» (пример №4). Это решение таково:
Опираясь на предыдущий пример №1, попробуйте составить ФСР самостоятельно, а потом сверить с ответом.
Ранг матрицы системы $r=3$ (поэтому у нас три базисных переменных), количество переменных $n=5$. Количество свободных переменных и количество решений ФСР равно $n-r=2$.
Так же, как и в предыдущем примере, составим ФСР. При составлении учтём, что $x_1$, $x_2$, $x_3$ – базисные переменные, а $x_4$, $x_5$ – свободные переменные.
Совокупность $\varphi_1=\left(\begin
$$ X=C_1\cdot\left(\begin
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Фундаментальная система решений: $\varphi_1=\left(\begin
Продолжение этой темы рассмотрим во второй части, где разберём ещё один пример с нахождением общего решения и ФСР.
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Линейная алгебра
- Элементарные преобразования. Ранг матрицы. Решение однородных систем уравнений.
Элементарные преобразования. Ранг матрицы. Решение однородных систем уравнений.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Элементарными преобразованиями матрицы называются следующие:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число, отличное от нуля;
3) прибавление к элементам строки (столбца) соответсвующих элементов другой строки (столбца), предварительно умноженных на некоторое число.
Пусть в матрице $A$ размера $m\times n$ выбраны произвольно $k$ строк и $k$ столбцов $(k\leq\min(m,n)).$ Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка $k,$ определитель которой называется минором $k-$го порядка матрицы $A.$
Максимальный порядок $r$ отличных от нуля миноров матрицы $A$ называется ее рангом, а любой минор порядка $r,$ отличный от нуля — базисным минором.
Основные методы вычисления ранга матрицы:
Метод окаймляющих миноров. Пусть в матрице найден минор $k$-го порядка $M,$ отличный от нуля. Рассмотрим лишь те миноры $(k+1)-$ го порядка, которые содержат в себе (окаймляют) минор $M:$ если все они равны нулю, то ранг матрицы равен $k.$ В противном случае среди окаймляющих миноров найдется ненулевой минор $(k+1)-$го порядка, и вся процедура повторяется.
Метод элементарных преобразований основан на том, что элементарные преобразования матрицы не меняют ее ранга. Используя эти преобразования матрицу можно привести к такому виду, когда все ее элементы кроме $a_<11>, a_<22>, . a_
Примеры.
3.150. Найти ранг матрицы методом окаймляющих миноров.
Решение.
Фиксируем минор отличный от нуля второго порядка $M_2=\begin
Таким образом, ранг матрицы $A$ равен двум.
Ответ: 2.
3.159. Вычислить ранг матрицы методом элементарных преобразований
Решение.
Производя последовательно элементарные преобразования, имеем
Ответ: 3.
3.160. Вычислить ранг матрицы методом элементарных преобразований
Решение однородных систем уравнений.
Пусть задана система $m$ линейных уравнений с $n$ неизвестными общего вида
или, в матричной форме, $AX=B,$ где
Если $B=0,$ то система называется однородной. В противном случае она называется неоднородной.
Система называется совместной если у нее существует хотя бы одно решение. В противном случае система называется несовместной.
Однородная система $AX=0$ всегда совместна поскольку имеет тривиальное решение $X=0.$ Для существования нетривиального решения необходимо и достаточно чтобы $r=rang A
Пусть $r=rang A.$ Не ограничивая общности, будем считать, что базисный минор располагается в первых $r$ $(1\leq r\leq\min(m, n))$ строках и столбцах матрицы $A.$ Отбросив последние $m-r$ уравнений системы получим укороченную систему $$\left\<\begin
$$\left\<\begin
Соответствующее решение укороченной, а, следовательно, и исходной систем имеет вид $X(c_1, . c_
Система вектор столбцов $E_1, . E_
Общее решение однородной системы имеет вид $X=c_1 E_1+. +c_
Всякая линейная комбинация решений однородной системы уравнений также является ее решением.
Примеры:
Найти фундаментальную систему решений и общее решение следующих систем:
3.223. $$\left\<\begin
Решение.
Матрица коэффициентов $A=\begin
Выберем в качестве базисного минор $M=\begin
Таким образом, общее решение системы $X(c_1)=\begin
Из общего решения находим фундаментальную систему решений: $E_1=X(1)=\begin
С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c_1)=c_1E_1.$
Ответ: $X(c_1)=c_1E_1;$ $E_1=\begin
3.225. $$\left\<\begin
Решение.
Матрица коэффициентов $A=\begin
Так как ранг равен количеству неизвестных, то система имеет только тривиальное решение.
Ответ: Система имеет только тривиальное решение.
3.227. $$\left\<\begin
Решение.
Вычислим ранг матрицы коэффициентов $A=\begin
Фиксируем минор отилчный от нуля второго порядка $M_2=\begin
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=\begin
По правилу Крамера находим $x_1$ и $x_2:$
Таким образом, общее решение системы $X(c_1,c_2)=\begin
Из общего решения находим фундаментальную систему решений: $E_1=X(1,0)=\begin
С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c_1, c_2)=c_1E_1+c_2E_2.$
Домашнее задание.
3.151.
Найти ранг матрицы методом окаймляющих миноров.
Ответ: 3.
3.154.
Найти ранг матрицы методом окаймляющих миноров.
Ответ: 2.
3.161.
Вычислить ранг матрицы методом элементарных преобразований
Ответ: 3.
3.164.
Вычислить ранг матрицы методом элементарных преобразований
Ответ: 2.
Найти фундаментальную систему решений и общее решение следующих систем:
3.224. $$\left\<\begin
Ответ: $X(c_1, c_2)=c_1E_1+c_2E_2;$ $E_1=\begin
3.226. $$\left\<\begin
Ответ: $X(c_1)=c_1E_1;$ $E_1=\begin
3.228. $$\left\<\begin
Элементарные преобразования системы линейных уравнений.
Алгебра и теория чисел
Лекция 3
Системы линейных уравнений
План
1. Основные понятия и обозначения.
2. Элементарные преобразования системы линейных уравнений.
3. Ступенчатая матрица. Приведение матрицы к ступенчатому виду.
Литература
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 25-48.
2. Ермаков В.И. Общий курс высшей математики. М.: Инфра — М, 2000. с. 5-22
3. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 38-56.
1. Основные понятия и обозначения. Простейшие системы двух линейных уравнений с двумя неизвестными изучаются в средней школе:

Известно, что справедлив один из следующих трех случаев: либо система имет одно решение, либо имеет бесконечно много решений, либо не имеет решений. В этом параграфе мы будем рассматривать общие системы линейных уравнений и установим это утверждение в общем случае кроме того изложим один из наиболее удобных методов решения систем линейных уравнений — метод последовательного исключения неизвестных или метод Гаусса по имени выдающегося немецкого математика К. Ф. Гаусса (1777-1855).
Определение 1.Системой m линейных уравнений с n неизвестными

где a11 ,a12 . amn — фиксированные числа (действительные, комплексные или принадлежащие некоторому полю) , называемые коэффициентами при неизвестных, b1 ,b2 . bm — фиксированные числа, называемые свободными членами.
Если все свободные члены в системе линейных уравнений равны нулю, то система линейных уравнений называется однородной.
Определение 2.Решением системы линейных уравнений (1) называется такой упорядоченный набор n чисел 
Система называется совместной, если она имеет хотя бы одно решение, и называется несовместной, если она не имеет решений. Совместная система называется определенной, если она имеет одно решение, и называется неопределенной, если она не имеет решений.
Пусть S1 , S2 системы линейных уравнений с одним и тем же числом неизвестных, X1 , X2 — множества их решений соответственно.
Определение 3.Говорят, что система линейных уравнений S2 следствие системы S1 и S2 , если каждое решение системы S1 является решением системы S2 ,т.е. 

Определение 4. Говорят, что системы S1 и S2 равносильны, если каждое решение системы S1 является решением системы S2 и каждое решение системы S2 является решением системы S1 , т.е. 

Отношение следования и равносильности обладают следующими свойствами.
1. Если 


Действительно, если 

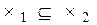



2. 
3. Если 

4. Если 
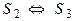
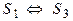
Свойства 2, 3, 4 доказываются аналогично.
Элементарные преобразования системы линейных уравнений.
Определение 5. Элементарными преобразованиями системы линейных уравнений называются ее следующие преобразования:
1) перестановка любых двух уравнений местами;
2) умножение обеих частей одного уравнения на любое число 
3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;
(при этом все остальные уравнения остаются неизменными).
Нулевым уравнением называем уравнение следующего вида:

Теорема 1. Любая конечная последовательность элементарных преобразований и преобразование вычеркивание нулевого уравнения переводит одну систему линейных уравнений в равносильную ей другую систему линейных уравнений.
Доказательство.В силу свойства 4 предыдущего пункта достаточно доказать теорему для каждого преобразования отдельно.
1. При перестановке уравнений в системе местами сами уравнения неизменяются, поэтому по определению полученная система равносильная первоначальной .
2. В силу первой части доказательства достаточно доказать утверждение для первого уравнения. Умножим первое уравнение системы (1) на число 

Пусть 






Умножая его на число k,получим верное числовое равенство:

т.о. устанавливаем, что 
Обратно, если 





Отсюда по определению 4 система (1) равносильна системе (2).
3. В силу первой части доказательства достаточно доказать утверждение для первого и второго уравнения системы . Прибавим к обеим частям первому уравнению системы соответствующие части второго умноженные на число k , получим систему

Пусть 




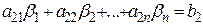
Прибавляя почленно к первому равенству второе, умноженное на число k получим верное числовое равенство:

Обратно, если 



Отсюда по определению 4 система (1) равносильна системе (5).
4. Так как нулевому уравнению удовлетворяет любой упорядоченный набор из n чисел, то при вычеркивании нулевого уравнения в системе получим систему равносильную исходной.
Ступенчатая матрица.
Определение 6.Матрицей размерности 
содержащая mn чисел, расположенных в m строк и n столбцов, числа 

Определение 7. Матрицей ступенчатого вида называется такая матрица, которая обладает свойствами:
1) в каждой строке матрицы имеется неравный нулю элемент;
2) в каждой строке матрицы, начиная со второй, первый слева неравный нулю элемент расположен правее первого слева неравного нулю элемента предыдущей строки матрицы.
Матрицу ступенчатого вида называют также трапециидальной матрицей, а квадратную матрицу ступенчатого вида называют треугольной матрицей. Ниже показаны две не ступенчатые матрицы и три ступенчатые матрицы (последняя матрица треугольная).







Определение 8. Элементарными преобразованиями строк матрицы называются следующие ее преобразования:
1) перестановка любых двух строк матрицы местами;
2) умножение одной строки матрицы на любое число 
3) прибавление к одной строке матрицы другой ее строки умноженной на любое число k ;
(при этом все остальные строки матрицы остаются неизменными).
Аналогично можно рассматривать элементарные преобразования столбцов матрицы.
Теорема 2. Любую ненулевую матрицу конечным числом элементарных преобразований и преобразований вычеркивания нулевой строки можно привести к матрице ступенчатого вида.
Доказательство.Доказательство проводим методом математической индукции по числу m строк матрицы. Для m=1 утверждение теоремы справедливо, так как ненулевая однострочная матрица по определению имеет ступенчатый вид.
Предположим, что утверждение теоремы доказано для матриц, имеющих m-1 строку и докажем его для матриц, в которых содержится m строк. Пусть первый слева отличный от нуля столбец данной матрицы имеет номер k , так как матрица ненулевая, то такой столбец найдется, и матрица имеет вид:
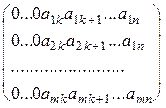
Можем считать, что элемент 




Рассмотрим матрицу, состоящую из последних m-1 строк матрицы (9):

Если матрица (10) нулевая, то все строки в матрице (9) кроме первой нулевые. Вычеркивая их, приходим к матрице ступенчатого вида. Если матрица (10) ненулевая, то по индуктивному предположению конечным число элементарных преобразований и преобразований вычеркивания нулевой строки может быть приведена к матрице ступенчатого вида: 
где элементы 



элементы 


4. Метод Гаусса. Системе линейных уравнений (1) соответствуют три матриц



Первая матрица называется матрицей системы, вторая — расширенной или присойдиненной матрицей системы, третья — столбцом свободных членов.
Система линейных уравнений называется системой ступенчатого вида, если расширенная матрица системы есть матрица ступенчатого вида. Неизвестные с коэффициентами неравными нулю, которые стоят первыми в уравнениях системы ступенчатого вида называются главными неизвестными, а остальные неизвестные называются свободными.
Линейное уравнение, в котором все коэффициенты равны нулю, а свободный член не равен нулю, т.е. уравнение вида:

не имеет решений. Действительно, если 

Пусть не все уравнения системы (1) нулевые. Тогда и расширенная матрица системы (1) ненулевая. По теореме 2 ее можно конечным числом элементарных преобразований и преобразований выбрасывания нулевой строки можно привести к матрице ступенчатого вида. Полученной матрице соответствует система линейных уравнений ступенчатого вида. Этим преобразованиям расширенной матрицы системы (1) соответствуют такие же преобразования системы линейных уравнений (1). По теореме 1 они переводят систему (1) в равносильную систему линейных уравнений, которая будет являются системой ступенчатого вида.
Таким образом мы доказали первую часть следующей теоремы.
Теорема 3.Любую систему линейных уравнений , содержащую ненулевое уравнение конечным числом элементарных преобразований и преобразований вычеркивания нулевого уравнения можно привести к равносильной ей системе ступенчатого вида. При этом возможны следующие три случая.
1. Если в полученной системе линейных уравнений ступенчатого вида есть противоречивое уравнение, то данная система не имеет решений.
2. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе равно числу неизвестных, то данная система имеет единственное решение.
3. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе меньше числа неизвестных, то данная система имеет бесконечно много решение.
Доказательство.Пусть дана система (1), содержащая ненулевое уравнение. По выше доказанному, она конечным числом элементарных преобразований она может быть преобразована к равносильной ей системе уравнений ступенчатого вида. Возможны случаи.
В полученной системе ступенчатого вида есть противоречивое уравнение. Тогда ни один набор чисел 
В полученной системе ступенчатого вида нет противоречивого уравнения. Тогда в каждом из уравнений системы ступенчатого вида содержится главное неизвестное. Отсюда получаем, что число главных неизвестных, а тем более число всех неизвестных, не менее числа уравнений в системе ступенчатого вида. Тогда возможны под случаи:
В системе ступенчатого вида число уравнений равно числу неизвестных, т. е. система имеет вид:

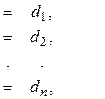
где 


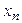




В системе ступенчатого вида число уравнений меньше числа неизвестных. В этом случае матрица полученной системы имеет вид (11), а
систему можно записать в виде:




где 




Следствие.Если в системе однородных уравнений число неизвестных больше числа уравнений, то система имеет бесконечно много решений.
Действительно, система однородных уравнений всегда имеет нулевое решение 
Метод исследования и решения систем линейных уравнений, изложенный в доказательстве теорем 3 называется методом Гаусса.
Пример 1.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Составим по полученной матрице ступенчатого вида систему линейных уравнений ступенчатого вида:
В полученной системе число уравнений равно числу неизвестных и полученная система имеет единственное решение, которое двигаясь вверх последовательно находим:
Решение системы 
Пример 2.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

http://mathportal.net/index.php/linejnaya-algebra/elementarnye-preobrazovaniya-rang-matritsy-reshenie-odnorodnykh-sistem-uravnenij
http://poisk-ru.ru/s39191t18.html

















