Однородная система линейных уравнений определитель ноль

Однородная система линейных уравнений определитель ноль

СИСТЕМА ОДНОРОДНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системой однородных линейных уравнений называется система вида

Ясно, что в этой случае , т.к. все элементы одного из столбцов в этих определителях равны нулю.

Так как неизвестные находятся по формулам , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.

Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0.

Итак, если определитель Δ ≠ 0, то система имеет единственное решение. Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений.

, а значит x=y=z=0.

СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ

Пусть задана квадратная матрица , X – некоторая матрица–столбец, высота которой совпадает с порядком матрицы A. .

Во многих задачах приходится рассматривать уравнение относительно X

,

где λ – некоторое число. Понятно, что при любом λ это уравнение имеет нулевое решение .

Число λ, при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A, а X при таком λ называется собственным вектором матрицы A.

Найдём собственный вектор матрицы A. Поскольку E∙X = X, то матричное уравнение можно переписать в виде или . В развёрнутом виде это уравнение можно переписать в виде системы линейных уравнений. Действительно .

И, следовательно,

Итак, получили систему однородных линейных уравнений для определения координат x₁, x₂, x₃ вектора X. Чтобы система имела ненулевые решения необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.

Это уравнение 3-ей степени относительно λ. Оно называется характеристическим уравнением матрицы A и служит для определения собственных значений λ.

Каждому собственному значению λ соответствует собственный вектор X, координаты которого определяются из системы при соответствующем значении λ.

Найти собственные векторы и соответствующие им собственные значения матрицы .

Составим характеристическое уравнение и найдём собственные значения

При λ₁ = –1 получаем систему уравнений

Если x₁ = t, то, где t Î R.
Если λ₂ = 5

ВЕКТОРНАЯ АЛГЕБРА. ПОНЯТИЕ ВЕКТРОРА

При изучении различных разделов физики встречаются величины, которые полностью определяются заданием их численных значений, например, длина, площадь, масса, температура и т.д. Такие величины называются скалярными. Однако, кроме них встречаются и величины, для определения которых, кроме численного значения, необходимо знать также их направление в пространстве, например, сила, действующая на тело, скорость и ускорение тела при его движении в пространстве, напряжённость магнитного поля в данной точке пространства и т.д. Такие величины называются векторными.

Введём строгое определение.

Направленным отрезком назовём отрезок, относительно концов которого известно, какой из них первый, а какой второй.

Вектором называется направленный отрезок, имеющий определённую длину, т.е. это отрезок определённой длины, у которого одна из ограничивающих его точек принимается за начало, а вторая – за конец. Если A – начало вектора, B – его конец, то вектор обозначается символом, кроме того, вектор часто обозначается одной буквой . На рисунке вектор обозначается отрезком, а его направление стрелкой.

Модулем или длиной вектора называют длину определяющего его направленного отрезка. Обозначается || или ||.

К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Он обозначается . Нулевой вектор не имеет определенного направления и модуль его равен нулю ||=0.

Векторы и называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. При этом если векторы и одинаково направлены, будем писать , противоположно .

Векторы, расположенные на прямых, параллельных одной и той же плоскости, называются компланарными.

Два вектора и называются равными, если они коллинеарны, одинаково направлены и равны по длине. В этом случае пишут .

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства.

1. Если дан вектор , то, выбрав любую точку , можем построить вектор , равный данному, и притом только один, или, как говорят, перенести вектор в точку .
   
2. Если рассмотреть квадрат ABCD, то на основанииопределения равенства векторов, мы можем написать и , но , , хотя все они имеют одинаковую длину.

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

Умножение вектора на число.

Произведением вектора на число λ называется новый вектор такой, что:

1. ;
2. вектор коллинеарен вектору ;
3. векторы и направлены одинаково, если λ>0 и противоположно, если λ

12. Однородная система линейных уравнений и ее решения

Система линейных уравнений

У которой столбец свободных членов — нулевой, называется однородной.

Однородная СЛУ (ОСЛУ) всегда совместна, так как нулевое решение (0,0,0) ей всегда удовлетворяет.

Поэтому, если однородная СЛУ имеет единственное решение, тогда оно — нулевое, так как для данного вида систем нулевое решение всегда имеет место.

Однородная СЛУ имеет ненулевые решения, если решений бесконечно много.

Утверждение 9. (Критерий существования ненулевых решений ОСЛУ).

Для того, чтобы однородная СЛУ имела ненулевые решения, необходимо и достаточно, чтобы определитель системы был равен нулю.

Пример №31. Решить однородную СЛУ

= = 30

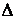
Определитель однородной системы отличен от нуля, следовательно решение единственное – нулевое.

Пример №32. Решить однородную СЛУ

= = 0

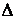
Определитель однородной системы равен нулю, следовательно — решений бесконечно много.

Общее решение ищем с помощью метода Гаусса

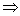
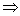
Далее записываем систему, соответствующую полученной ступенчатой матрице, и являющуюся эквивалентной исходной.

=> => ,

Однородные СЛАУ. Фундаментальная система решений

Однородные СЛАУ

Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.

Однородная СЛАУ, записанная в матричном виде, $A X=\Theta$ всегда совместна, так как $X=\Theta$ всегда является ее решением.

Заметим, что если $x_<1>, x_<2>$ — это два решения однородной СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:

$$Y=\lambda_ <1>x_<1>+\lambda_ <2>x_<2>$$ $$A Y=A\left(\lambda_ <1>x_<1>+\lambda_ <2>x_<2>\right)=\lambda_ <1>A x_<1>+\lambda_ <2>A x_<2>=\lambda_ <1>\Theta+\lambda_ <2>\Theta=\Theta$$

Если однородная квадратная СЛАУ имеет ненулевое решение, то определитель матрицы системы равен нулю.

Задание. Выяснить, имеет ли однородная СЛАУ $\left\<\begin 3 x-2 y=-1 \\ x+3 y=7 \end\right.$ ненулевые решения.

$$\Delta=\left|\begin 3 & -2 \\ 1 & 3 \end\right|=9-(-2)=9+2=11 \neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Фундаментальная система решений

Рассмотрим множество всех столбцов, которые являются решениями исходной системы.

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

Задание. Найти общее решение и ФСР однородной системы $\left\<\begin x_<1>+x_<2>-3 x_<4>-x_<5>=0 \\ x_<1>-x_<2>+2 x_<3>-x_<4>=0 \\ 4 x_<1>-2 x_<2>+6 x_<3>+3 x_<4>-4 x_<5>=0 \\ 2 x_<1>+4 x_<2>-2 x_<3>+4 x_<4>-7 x_<5>=0 \end\right.$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=\left(\begin 1 & 1 & 0 & -3 & -1 \\ 1 & -2 & 2 & -1 & 0 \\ 4 & -2 & 6 & 3 & -4 \\ 2 & 4 & -2 & 4 & -7 \end\right)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & -6 & 6 & 15 & 0 \\ 0 & 2 & -2 & 10 & -5 \end\right)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 9 & -3 \\ 0 & 0 & 0 & 12 & -4 \end\right)$$

От четвертой строки отнимем $\frac<4><3>$ третьей и третью строку умножим на $\frac<1><3>$ :

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \\ 0 & 0 & 0 & 0 & 0 \end\right)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \end\right)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A \sim\left(\begin 1 & 1 & 0 & -6 & 0 \\ 0 & -2 & 2 & 5 & 0 \\ 0 & 0 & 0 & 3 & -1 \end\right)$$

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

Здесь $x_<2>, x_<4>$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_<1>, x_<3>, x_<5>$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).

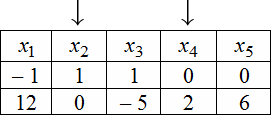
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения $x_<2>=1$ , $x_<4>=0$ получаем, что $\left\<\begin x_<1>=-1+6 \cdot 0=-1 \\ x_<3>=1-\frac<5> <2>\cdot 0=1 \\ x_<5>=3 \cdot 0=0 \end\right.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_<2>=0$ , $x_<4>=2$, будем иметь, что =12, x_<3>=-5, x_<5>=6> , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$X_<1>=\left(\begin -1 \\ 1 \\ 1 \\ 0 \\ 0 \end\right), X_<2>=\left(\begin 12 \\ 0 \\ -5 \\ 2 \\ 6 \end\right)$$

Общее решение является линейной комбинацией частных решений:

$$X=C_ <1>X_<1>+C_ <2>X_<2>=C_<1>\left(\begin -1 \\ 1 \\ 1 \\ 0 \\ 0 \end\right)+C_<2>\left(\begin 12 \\ 0 \\ -5 \\ 2 \\ 6 \end\right)$$

где коэффициенты $C_<1>, C_<2>$ не равны нулю одновременно. Или запишем общее решение в таком виде:

Придавая константам $C_<1>, C_<2>$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.