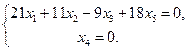Однородная система линейных уравнений связь с неоднородной

Связь решений однородной и неоднородной систем линейных уравнений

Пусть (25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется соответствующей однородной системой (это система (30)). Решения систем (25) и (30) удовлетворяют следующим свойствам:

(30)	1 0 . Сумма решений данной неоднородной и соответствующей однородной системы линейных уравнений есть решение данной неоднородной системы. Пусть а – частное решение системы (25) и с – частное решение системы (30). Рассмотрим вектор (а + с).

Системы (25) и (30) в векторной форме имеют вид А×х = в (31) и А×х= 0 (32). По условию А×а = в, А×с= 0. Следовательно, А×(а + с) = А×а+ А×с= в + 0 = в. Следовательно, (а + с) – решение уравнения (31), а поэтому и системы (25).

2 0 . Разность двух решений неоднородной системы линейных уравнений есть решение соответствующей однородной системы.

Пусть а и с –решения системы (25), а следовательно, и уравнения (31), т.е. А×а = в и А×с = в. Тогда А×(а – с) = А×а – А×с= в – в = 0, т.е. (а – с) – решение уравнения (32), а поэтому и системы (30).

3 0 . Если а – фиксированное частное решение системы (25), а с пробегает все решения системы (30), то (а + с) пробегает все решения системы (25).

Согласно 1 0 , при любом свектор(а + с) будет решением системы (25). Если d – любое решение системы (25), то, согласно 2 0 , разность (d – а) будет решением системы (30). Обозначив (d – а) = с, получим d = (а + с).

Теорема 29. Если а – частное решение линейной неоднородной системы уравнений и а₁, а₂, …, а_n–r – фундаментальная система решений соответствующей однородной системы уравнений, то общее решение данной неоднородной системы имеет вид

(Иными словами, общее решение системы линейных неоднородных уравнений равно сумме частного решения этой системы и общего решения соответствующей однородной системы.)

Доказательство является следствием предыдущих свойств.

Задание подпространств конечномерного линейного пространства с помощью систем линейных уравнений

Пусть дано n-мерноелинейное пространство L и пусть в нём зафиксирован базис е = (е₁, е₂,… , е_n ). Пусть М – линейное подпространство в L .

Определение 30. Будем говорить, что система линейных уравнений задаёт подпространство М, если этой системе удовлетворяют координаты всех векторов из М и не удовлетворяют координаты никаких других векторов.

Из свойств решений однородной системы линейных уравнений следует, что любая однородная линейная система уравнений ранга r с n переменными задаёт в любом n-мерном пространстве L_n (если в нём зафиксирован базис) (n–r )-мерное линейное подпространство.

Справедливо и обратное утверждение. А именно, имеет место следующая теорема.

Теорема 30.Если в линейномn-мерном пространстве L_n зафиксирован базис, то любое его к-мерное линейное подпространство можно задать системой линейных однородных уравнений с n неизвестными ранга (n – к).

Доказательство.Пусть в L_n зафиксирован базис е = (е₁, е₂,… , е_n ). Пусть L_к – линейное к-мерное подпространство в L_n . Выберем в L_к любой базис а = (а₁, а₂, … , а_к). Пусть В матричной форме а = е × А, где А = .

Так как а – базис, то ранг матрицы А равен к.

Если d – любой вектор, то d Î L_к Û d = с₁а₁ + с₂а₂ + … +с_ка_к ,где с₁, с₂, … , с_к независимо друг от друга пробегают все элементы поля Р. Их называют параметрами. В матричном виде d = а × с, где с –столбец параметров. Отсюда d = е×(А×с). Если х – столбец координат вектора а в базисе е, то d = е×х. Отсюда, е×х = е×(А×с) и х = А×с. Распишем в координатном виде.

Получили параметрические уравнения, определяющие Lк . После исключения параметров получится система (n – к) линейных однородных уравнений. Векторы а1, а2, … , ак являются её линейно независимыми решениями. Все остальные решения являются их линейными комбинациями.

Следовательно, система векторов (а₁, а₂, … , а_к) будет фундаментальной системой решений полученной системы уравнений и поэтому ранг этой системы уравнений равен (n – к).

Пример. В пространстве L₅ зафиксирован базис е = (е₁, е₂, е₃, е₄ , е₅ ). Найти систему линейных однородных уравнений, задающих L₃ = , если а₁ = (1, –2, 2, 0, 1), а₂ = (0, 4, 7, 0, 1), а₃ = (–2, 3, –1, 0, 0).

Решение. Найдём ранг системы векторов (а₁, а₂, а₃ ). Для этого достаточно найти ранг матрицы . Минор . Окаймляющий минор ¹ 0, следовательно, ранг матрицы равен 3, т.е. векторы а₁, а₂, а₃ линейно независимы и подпространство L₃ – трёхмерное. Согласно доказанной теоремы, оно может быть задано системой линейных однородных уравнений ранга 2.

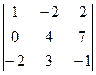
d Î L₃ Û d = с₁а₁+ с₂а₂+ с₃а₃. Отсюда d Î L₃ Û х₁ = с₁ – 2с₃ , х₂ = –2с₁ + 4с₂ + 3с₃ , х₃ = 2с₁ + 7с₂ – с₃ , х₄ = 0, х₅ = с₁ + с₂. Если из первого второго и пятого уравнений выразить с₁, с₂ и с₃ и подставить их в третье и четвёртое уравнения, то получим следующую систему

Замечание. Очевидно, система, задающая данное подпространство, определяется не единственным образом. К найденным уравнениям можно добавлять новые уравнения, являющиеся их линейными комбинациями.

22. Связь решений однородной и неоднородной систем линейных уравнений

Пусть (25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется Соответствующей однородной системой (это система (30)). Решения систем (25) и (30) удовлетворяют следующим свойствам:

(30)

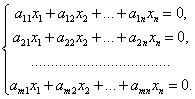
10. Сумма решений данной неоднородной и соответствующей однородной системы линейных уравнений есть решение данной неоднородной системы. Пусть А – частное решение системы (25) и С – частное решение системы (30). Рассмотрим вектор (А + С).

20. Разность двух решений неоднородной системы линейных уравнений есть решение соответствующей однородной системы.

30. Если А – фиксированное частное решение системы (25), а С пробегает все решения системы (30), то (А + С) пробегает все решения системы (25).

Согласно 10, при любом С Вектор (А + С) будет решением системы (25). Если D – любое решение системы (25), то, согласно 20, разность (D – А) будет решением системы (30). Обозначив (D – А) = С, получим D = (А + С).

Теорема 29. Если А – частное решение линейной неоднородной системы уравнений и А1, а2, …, аn–r – фундаментальная система решений соответствующей однородной системы уравнений, то общее решение данной неоднородной системы имеет вид

(Иными словами, общее решение системы линейных неоднородных уравнений равно сумме частного решения этой системы и общего решения соответствующей однородной системы.)

Доказательство Является следствием предыдущих свойств.

Структура общего решения системы уравнений

Однородная система линейных уравнений

всегда совместна, так как имеет тривиальное решение . Если ранг матрицы системы равен количеству неизвестных , то тривиальное решение единственное. Предположим, что . Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица однородной системы при элементарных преобразованиях строк приводится к упрощенному виду , т.е. . Поэтому из (5.11) получаем общее решение однородной системы уравнений :

Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.

Свойства решений однородной системы уравнений

1. Если столбцы — решения однородной системы уравнений, то любая их линейная комбинация также является решением однородной системы.

В самом деле, из равенств следует, что

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеет линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность линейно независимых решений однородной системы называется фундаментальной системой (совокупностью) решений .

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества линейно независимых решений.

Теорема 5.3 об общем решении однородной системы. Если — фундаментальная система решений однородной системы уравнений (5.4), то столбец

при любых значениях произвольных постоянных также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.14).

Прямое утверждение теоремы следует из свойства 1 решений однородной системы. Докажем обратное утверждение о том, что любое решение можно представить в виде (5.14). Для этого составим матрицу , приписав к столбцам фундаментальной системы решений столбец

Найдем ранг этой матрицы. Так как первые столбцов линейно независимы, то . Так как каждый из столбцов матрицы является решением системы , то по первой формуле из (5.13) получаем

Следовательно, первая строка матрицы является линейной комбинацией последних строк этой матрицы.

По второй формуле из (5.13) получим, что вторая строка матрицы является линейной комбинацией последних строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы является линейной комбинацией последних строк этой матрицы. Значит, первые строк матрицы можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, , так как после вычеркивания в матрице будет всего строк. Таким образом, . Значит, есть базисный минор матрицы , который расположен в первых ее столбцах, а столбец не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа , что

Итак, обратное утверждение доказано.

Алгоритм решения однородной системы уравнений

1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).

Если ранг матрицы системы равен числу неизвестных , то система имеет единственное тривиальное решение и процесс решения заканчивается.

Если ранг матрицы системы меньше числа неизвестных , то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.

6. Найти фундаментальную систему решений однородной системы. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).

7. Записать общее решение однородной системы по формуле (5.14).

1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.

2. Матрица столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде

3. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы

Тогда блочная матрица размеров является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.

Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы

Решение. 1. Составляем расширенную матрицу системы

2-4. Используя элементарные преобразования над строками матрицы , приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):

Пункт 3 метода Гаусса пропускаем.

5. Переменные — базисные, а — свободные. Записываем формулу (5.13) общего решения однородной системы

6. Находим фундаментальную систему решений. Так как и , надо подобрать линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:

В результате получили фундаментальную систему решений

7. Записываем общее решение однородной системы по формуле (5.14):

Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, и . Тогда получим другую фундаментальную систему решений

Несмотря на различия, обе формулы задают одно и то же множество решений.

Структура общего решения неоднородной системы уравнений

Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.

Рассмотрим неоднородную систему и соответствующую ей однородную систему . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений и неоднородной системы есть решение однородной системы.

Действительно, из равенств и следует, что .

2. Пусть — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде

В самом деле, для любого решения неоднородной системы разность по свойству 1 является решением однородной системы, т.е. — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть — решение неоднородной системы, а — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

при любых значениях [i]произвольных постоянных является решением неоднородной системы, и, наоборот, для каждого решения этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Алгоритм решения неоднородной системы уравнений

1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).

6. Найти частное решение неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему ее решений. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

1. Используя фундаментальную матрицу однородной системы , решение неоднородной системы можно представить в виде

2. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы

Тогда блочная матрица оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

где — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:

Переменные — базисные, а — свободные.

6. Полагая , получаем частное решение неоднородной системы .

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

8. Записываем по формуле (5.15) общее решение неоднородной системы

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом , используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

Записываем частное решение неоднородной системы

и составляем фундаментальную матрицу:

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):