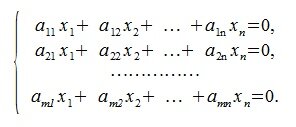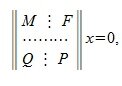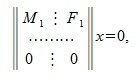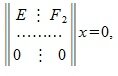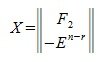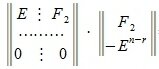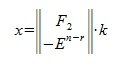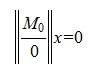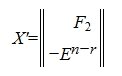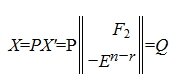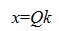Однородная система уравнений условие ненулевого решения однородной

53. Однородные системы уравнений

Линейное уравнение называется Однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:

Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы.

Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.

Доказательство: Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что не превосходит . В случае система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при .

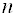
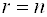
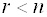
Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.

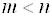
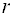
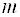
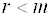
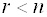
Доказательство: Если у системы уравнений , то ранг системы не превышает числа уравнений , т. е. . Таким образом, выполняется условие и, значит, система имеет ненулевое решение.

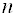
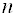
Следствие 2: Однородная система уравнений с неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.

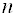
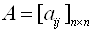
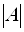
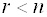
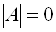
Доказательство: Допустим, система линейных однородных уравнений, матрица которой с определителем , имеет ненулевое решение. Тогда по доказанной теореме , а это значит, что матрица вырожденная, т. е. .

Определение общего решения СЛУ. Базисные и свободные неизвестные.

Системой уравнений называется общим решением совместная система A1x1+A2x2+…+Anxn=B (1), если выполняется следующее условие:
A1’x1+A2’x2+…+An’xn=B (2)
система (2) общее решение сист. (1)
условия:1)система (1) и (2) должны быть равносильны
2)система векторов A1,A2. An в сист. уравнений (2) явл. Разрешённой системой векторов

Набор неизвестных системы уравнения (1) называются базисными, если векторы при этих неизвестных образуют базис системы A1A2…An
не базисные неизвестные принято называть свободными.

Однородные СЛУ. Свойства однородной СЛУ. Теорема о нулевом и ненулевом решении СЛУ,

Однородная система — система, у которой все свободные члены равны нулю.

Однородная система—всегда совместна, так как x₁=x₂=x₃=. =x_n=0является решением системы.

Теоремы о ненулевых решениях однородной системы :

Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т. е. r

а) вектора F1,F2..Fk линейно-независимы

б) k=n-r(A) – число решений равно разности количества неизвестных и ранга системы

Теорема об условии существования ФСР однородной СЛУ

Любое линейное однородное дифференциальное уравнение n -го порядка с непрерывными коэффициентами имеет фундаментальную систему решений, т.е. систему из n линейно независимых решений.

Однородная система линейных уравнений

Рассмотрим систему линейных уравнений (СЛУ):

Представим (1) в матричном виде:

где A m×n матрица, x вектор столбец порядка n , 0 — нулевой вектор столбец порядка m.

СЛУ (1) (или (2)) называется однородной системой линейных уравнений, т.к. правая часть системы равна нулю.

Однородная система линейных уравнений всегда совместна, т.к. вектор 0 всегда является решением системы (1):

Это решение называется нулевым или тривиальным решением.

1. Cистема линейных однородных уравнений имеет ли другие решения, кроме нулевого.
2. При каких условиях система линейных однородных уравнений имеет нетривиальное решение.
3. Как найти множество всех решений системы однородных линейных уравнений.

Если A n×n матрица и rank( A)= n, то нулевой вектор является единственным решением системы (1), в противном случае система имеет множество решений.

Обшее решение однородной системы линейных уравнений

Пусть A m×n — матрица rank A=r. В общем случае можем предположить что r r столбцов матрицы A линейно независимы. Для удобства записи предположим, что это первые r столбцы матрицы A. Переставляя строки матрицы можно добиться того, чтобы подматрица матрицы A порядка r×r, расположенная в левом верхнем углу, была невырожденной. Запишем систему (2) в блочном виде:

где M — r×r — матрица, rang M=r.

Применяя метод исключения Гаусса для системы (3), получим:

где M₁ верхняя треугольная матрица, 0 — нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:

где E — единичная матрица порядка r×r.

где F₂— r×(n-r) — матрица, E n-r — единичная матрица порядка n-r, X — матрица порядка n×(n-r).

В уравнении (5) вместо x подставляя матрицу (6), получим:

Таким образом, векторы столбцы матрицы X являются решением системы (2) (или (1)). Более того, эти векторы линейно независимы и их линейная комбинация также является решением (2).

Общее решение системы однородных линейных уравнений имеет следующий вид:

гдe k — произвольный вектор столбец порядка n-r.

Общее решение системы однородных линейных уравнений можно также записать в следующем виде:

где x_i — i-ый вектор-столбец матрицы X, а k_i — i-ая координата вектора k

Множество всех решений (8)(или (9)) образует ядро или нуль пространство матрицы A и обозначается через Ker (A) или N(A).

В начале этого параграфа мы предполагали, что линейные независимые r векторы столбцы расположены в начале матрицы A. В общем случае, если они расположены в произвольных местах, аналогично вышеизложенному, применяя метод Гаусса, затем обратный ход Гауссова исключения и, наконец , разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует), получим

Сделаем замену переменных:

где P -матрица перестановок поядка n×n выбрана так, чтобы при подстановке (11) в (10) получили:

где E — единичная матрица порядка r×r.

Аналогично вышеизложенному векторы столбцы матрицы X’:

образуют множесво всех решений однородной системы линейных уравнений (12).

Учитывая (11) получим:

Общее решение системы однородных линейных уравнений имеет следующий вид:

гдe k — произвольный вектор столбец порядка n-r.

Общее решение системы однородных линейных уравнений можно также записать в следующем виде:

где q_i — i-ый вектор-столбец матрицы Q, а k_i — i-ая координата вектора k

Нахождение общего решения однородной системы линейных уравнений с помощью псевдообратной матрицы

Если rank(A)= r, r общее решение можно представить в следующем виде:

где E —единичная матрица, A + — псевдообратная к A матрица.

Для проверки подставим (16) в (2):

Ax=A(E−A + A)z=(A−AA + A)z=(A−A)z=0.

Ранг матрицы rank( E−A + A)= n-r. Следовательно столбцы матрицы E−A + A образуют множество всех решений системы (2).

Отметим, что r столбцов матрицы E−A + A линейно зависимы. Для исключения линейно зависимых столбцов можно сделать скелетное разложение. Тогда E−A + A= QS, где Q n×n−r — матрица rank (Q)=n−r, S n−r×n-матрица rank (S)=n−r. Тогда множество всех решений однородной системы линейных уравнений примет следующий вид:

Решение однородной системы линейных уравнений онлайн

Для решения однородной системы линейных уравнений пользуйтесь онлайн калькулятором который решает однородную систему по шагам и находит полное решение.