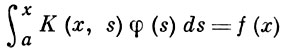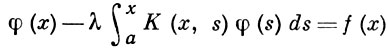Однородное интегральное уравнение вольтерра 1 го рода

Решения интегральных уравнений онлайн

В этом разделе мы рассмотрим типовые задачи по интегральным уравнениям с решениями. Интегральное уравнение содержит неизвестную функцию под знаком интеграла (по аналогии как дифференциальное — функцию под знаком дифференциала:)).

Выделяют два основных класса интегральных уравнений: уравнения Фредгольма I и II рода:

$$ (I) \quad \int_a^b K(x,s)u(s)ds = f(x),\\ (II) \quad u(x)=\int_a^b K(x,s)u(s)ds + f(x). $$

В случае переменного верхнего предела интегрирования получаем соответственно уравнение Вольтерра I и II рода:

$$ (I) \quad \int_a^x K(x,s)u(s)ds = f(x),\\ (II) \quad u(x)=\int_a^x K(x,s)u(s)ds + f(x). $$

Это линейные неоднородные уравнения (при $f(x)=0$ — однородные), иногда рассматриваются более общий случай с параметром $\lambda$ перед интегралом.

Ниже вы найдете примеры нахождения решений интегральных уравнений, собственных значений и функций, исследования ядра, применения интегральных уравнений для решения других задач.

Примеры решений интегральных уравнений

Задача 1. Пользуясь теоремой Гильберта-Шмидта, исследовать и решить интегральное уравнение 2-го рода $(E+\lambda A)x=y$ в гильбертовом пространстве $X$.

Задача 2. Найти собственные значения и собственные функции уравнения:

$$ y(x)=\lambda \int_0^1 (\cos 2\pi x +2x \sin 2\pi t +t \sin \pi x)y(t)dt. $$

Задача 3. Решить уравнение Вольтерры, сведя его к обыкновенному дифференциальному уравнению.

Задача 4. Решить или установить неразрешимость уравнений с вырожденным ядром.

Задача 5. Решить интегральное уравнение, сведя его предварительно к обыкновенному дифференциальному уравнению.

Задача 6. Найти резольвенту для интегрального уравнения Вольтерры со следующим ядром $K(x,t)=x^<1/3>t^<2/3>$.

Задача 7. Исследовать решения уравнения с вырожденным ядром при различных значениях параметра $\lambda$ (ограничиться случаем вещественных характеристических чисел).

$$ y(x)-\lambda \int_0^1 x y(t)dt = \sin 2\pi x. $$

Задача 8. Для симметричного ядра $$K(x,t) = \frac<1> <2>\sin |x-t| \quad (0 \le, x,t \le \pi)$$ найти характеристические числа и соответствующие им собственные функции, сводя интегральное уравнение к однородной краевой задаче для обыкновенного дифференциального уравнения.

Задача 9. Решить краевую задачу, используя функцию Грина

Задача 10. Применяя преобразование Лапласа, решить интегральное уравнение

Помощь с интегральными уравнениями

Если вам нужна помощь с решением задач и контрольных по интегральным уравнениям (и другим разделам математического и функционального анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 200 рублей , оформление производится в Word, срок от 1 дня.

ВОЛЬТЕРРА УРАВНЕНИЕ

ВОЛЬТЕРРА УРАВНЕНИЕ — интегральное уравнение вида

(линейное интегральное В. у. I рода) или вида

(линейное интегральное В. у. II рода). Здесь х, s, а — действительные числа, λ (вообще говоря) — комплексный параметр, φ(s) — неизвестная функция, f(x), К(х, s) — заданные функции, суммируемые с квадратом соответственно на отрезке [а, b] и в области a ≤ x ≤ b, a ≤ s ≤ x. При этом функция f(x) наз. свободным членом В. у., а функция К(х, s) -ядром В. у.

В. у. могут рассматриваться как частный вид Фредгольма уравнений, когда ядро К(х, s), задаваемое на квадрате a ≤ x ≤ b, a ≤ s ≤ b, обращается в нуль в треугольнике a ≤ x

О семействах решений интегральных уравнений Вольтерры первого рода с разрывными ядрами Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Сидоров Денис Николаевич

Предложен метод построения параметрических семейств непрерывных решений одного класса интегральных уравнений Вольтерры первого рода , возникающих в теории развивающихся систем. Ядра рассматриваемых уравнений допускают разрывы первого рода на монотонно возрастающих кривых. В явном виде построено характеристическое алгебраическое уравнение. Отдельно изучается регулярный случай, когда характеристическое уравнение не имеет натуральных корней и решение интегрального уравнения единственное. В нерегулярном случае характеристическое уравнение имеет натуральные корни, а решение рассматриваемого интегрального уравнения содержит произвольные постоянные. При этом решение может быть неограниченными, если характеристическое уравнение имеет нулевой корень. Показано, что число произвольных постоянных, входящих в решение, зависит от кратности натуральных корней характеристического уравнения. Доказаны теоремы существования параметрических семейств решений и строится их асимптотика с помощью логарифмо-степенных полиномов . Асимптотика может уточняться численно или последовательными приближениями .

Похожие темы научных работ по математике , автор научной работы — Сидоров Денис Николаевич

SOLUTION TO THE VOLTERRA INTEGRAL EQUATIONS OF THE FIRST KIND WITH DISCONTINUOUS KERNELS

The method of parametric families of continuous solutions construction for the Volterra integral equations of the first kind arising in the theory of developing systems is proposed. The kernels of these equations admit a first-order discontinuities on the monotone increasing curves. The explicit characteristic algebraic equation is constructed. In the regular case characteristic equation has no positive roots and solution of the integral equation is unique. In irregular case the characteristic equation has natural roots and the solution contains arbitrary constants. The solution can be unbounded if characteristic equation has zero root. It is shown that the number of arbitrary constants in the solution depends on the multiplicity of positive roots of the characteristic equation. We prove existence theorem for parametric families of solutions and built their asymptotics with logarithmic power polynomials . Asymptotics can be specified numerically or using the successive approximations.

Текст научной работы на тему «О семействах решений интегральных уравнений Вольтерры первого рода с разрывными ядрами»

О СЕМЕЙСТВАХ РЕШЕНИЙ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ВОЛЬТЕРРЫ ПЕРВОГО РОДА С РАЗРЫВНЫМИ ЯДРАМИ

Предложен метод построения параметрических семейств непрерывных решений одного класса интегральных уравнений Вольтерры первого рода, возникающих в теории развивающихся систем. Ядра рассматриваемых уравнений допускают разрывы первого рода на монотонно возрастающих кривых. В явном виде построено характеристическое алгебраическое уравнение. Отдельно изучается регулярный случай, когда характеристическое уравнение не имеет натуральных корней и решение интегрального уравнения единственное. В нерегулярном случае характеристическое уравнение имеет натуральные корни, а решение рассматриваемого интегрального уравнения содержит произвольные постоянные. При этом решение может быть неограниченными, если характеристическое уравнение имеет нулевой корень. Показано, что число произвольных постоянных, входящих в решение, зависит от кратности натуральных корней характеристического уравнения. Доказаны теоремы существования параметрических семейств решений и строится их асимптотика с помощью логарифмо-степенных полиномов. Асимптотика может уточняться численно или последовательными приближениями.

Ключевые слова: интегральное уравнение Вольтерры первого рода, асимптотика, разрывное ядро, последовательные приближения, логарифмо-степенные полиномы.

Рассматривается интегральное уравнение Вольтерры первого рода:

где ядро определено формулой

В этой норме неравенство (8) сохранится, и при достаточно большом I оператор А будет

Тогда уравнение (1) в классе С(о,т] имеет решение

где функция и(£) € С[о,т] строится единственным образом, методом последовательных приближений.

Доказательство. Доказательство вытекает из следствия 1. Действительно, используя замену (11) уравнение (1) преобразуется к уравнению

У К (t,s)sN u(s)ds = g(t), (12)

g(t) = —J K(t,s)sNxN(s)ds + f (t) (13)

удовлетворяет условию следствия 1. Поэтому в представлении (11) функция u(t) строится последовательными приближениями единственным образом из уравнения (10) при любом начальном приближении. □

Определение 1. Уравнение (12) с правой частью (13) назовем регуляризацией уравнения (1), а функцию xN (t) — асимптотическим приближением решения (11) уравнения (1).

Введение этого определения связано с тем, что функцию u(t) можно строить, решая уравнение (12) численно, используя хорошо исследованные квадратурные схемы (см. библиографию в [3]). Способ построения асимптотических приближений xN(t) в решении (12) рассмотрим ниже в п.3.

2. Построение асимптотического приближения xN (t) решения

Пусть наряду с условием A выполнено условие B. Функции Ki(t,s),i = 1, n, f (t) дифференцируемые N + 1 раз в окрестности нуля, где N выбирается, используя условие A.

Введем вспомогательное алгебраическое уравнение относительно j из N

L(j) = Е K(0,0)(al+j — ) = 0 (14)

и назовем его характеристическим уравнением интегрального уравнения (1).

Так как f(0) = 0, то уравнение

эквивалентно уравнению (1).

Асимптотическое приближение его решения будем искать в виде полинома хм (Ь) =

Методом неопределенных коэффициентов с учетом неравенств 0 = ао и, то К1 (0, 0) = К2(0, 0) = .

■ ■ ■ = Кп-1(0, 0) = Кп(0, 0) в силу (18), т.к. ёе! ||аг||г г=щ = 0. Но тогда в силу (17) Кп(0, 0) =

0, что противоречит условию Л.

При выполнении условий Л, В возможны два случая.

2.1. Регулярный случай

Пусть 1(3) =0,3 € N. Тогда Л = 1 не удовлетворяет ни одному из характеристиче-

ских уравнений в последовательности (16). Все коэффициенты Хг асимптотики хм = ^ Хг1г

определятся однозначно методом неопределенных коэффициентов и не зависят от 1п Ь.

Из изложенного вытекает следующая теорема

Теорема 2. Пусть выполнены условия Л, В и Ь(3) =0,3 € N. Тогда уравнение (1) имеет

деленных коэффициентов, а функция п(Ь) строится затем однозначно последовательными приближениями, или численно из уравнения (12).

2.2. Нерегулярный случай

Пусть Ь(3) = 0 только при 3 € <31. ,3к>С <0,1. N>, и при этом кратность корня Л = 1 соответствующего характеристического уравнения в последовательности (16) равна

Пусть в 3-ом разностном уравнении (15) правая часть Му (г) оказалась полиномом от г порядка иу > 0.

Тогда в нерегулярном случае, т.е. при Гу > 1, на основании ( [17], с. 338) частное решение

3-го уравнения (15) надо искать в виде полинома Х(г) = ^ Сггг.

Коэффициенты Сг этого полинома вычисляются методом неопределенных коэффициентов последовательно, начиная со старшего спз +3. Коэффициент Ху (г) искомого асимптотического приближения xN в этом случае имеет вид

Xj (z) = Со + CiZ +-+ Crj-1 + X(z).

В нерегулярном случае, когда rj > 1, постоянные Со. crj-i останутся произвольными, т.к. тогда функции zi, i = 0,1. ,rj — 1 удовлетворят j-му однородному разностному уравнению, отвечающему (15).

На практике, используя свойство 1, коэффициент Xj (z) в нерегулярном случае можно

строить непосредственно в виде полинома Ciz%, определяя последовательно Сп. +r ., . . . ,Со

i=0 3 3 методом неопределенных коэффициентов. При этом числа сг.-i. ,Со останутся произвольными. Таким образом, в нерегулярном случае, когда L(j) = 0 при натуральном j, при определении коэффициента Xj (z) появляются rj новых произвольных постоянных. Порядок полинома Xj (z) на величину кратности rj корня Л = 1 характеристического уравнения (16) станет больше порядка nj правой части уравнения (15), то есть порядка полинома Mj (z). Из выше изложенного вытекает основная теорема:

Теорема 3. Пусть выполнены условия A, B. Пусть характеристическое уравнение L(j) =

0 интегрального уравнения (1) имеет ровно k натуральных корней . Пусть при этом корень Л = 1 j-го характеристического уравнения (16) имеет кратность rj. Тогда уравнение (1) в С(о,т] имеет решение

x = Е xi(ln t)ti + tN u(t), (20)

которое зависит от p = ri + ■ ■ ■ + rk произвольных постоянных. Более того, коэффициенты Xi асимптотического приближения xN (t) являются полиномами от ln t возрастающих порядков, не превосходящих p. Функция u(t) по вычисленному асимптотическому приближению с фиксированными постоянными строится последовательными приближениями, равномерно сходящимися при t € [0,T], либо численно из уравнения (12).

Замечание 1. Если L(0) =0, то в решении (20) Xo = const + a ln t, a — определенная постоянная. Поэтому в этом случае x(t) € C(o,T], limox(t) = ж.

Замечание 2. Изложенные результаты допускают обобщение в случае, когда в уравнении (1) при ai-l(t) П696 от 30 мая 2010 г., также частично поддержана РФФИ, проекты 12-01-00722 и 11-08-00109.

1. Lyapunov-Schmidt methods in nonlinear analysis and applications / N.A. Sidorov,

B.V. Loginov, A.V. Sinitsyn, M.V. Falaleev. — Dordrecht: Kluwer Academic Publishers, 2002.

2. Sviridyuk, G.A. Linear Sobolev type equations and degenerate semigroups of operators / G.A. Sviridyuk, V.E. Fedorov. — Utrecht; Boston: VSP, 2003. — 216 p.

3. Апарцин, А.С. Неклассические уравнения Вольтерра I рода: теория и численные методы / А.С. Апарцин. — Новосибирск: Наука, 1999. — 193 с.

4. Маркова, Е.В. О моделях развивающихся систем типа Глушкова и их приложениях в электроэнергетике / Е.В. Маркова, И.В. Сидлер, В.В. Труфанов // Автоматика и телемеханика. — 2011. — №7.- С. 20 — 28.

5. Denisov, A.M. On a special Volterra integral equation of the first kind / A.M. Denisov, A. Lorenzi // Boll. Un. Mat. Ital. B. — 1995.- V. 7, №9. — P. 443 — 457.

6. Яценко, Ю.П. Интегральные модели систем с управляемой памятью / Ю.П. Яценко. -Киев: Наукова думка, 1991. — 218 с.

7. Evans, G.C. Volterra’s Integral Equation of the Second Kind with Discontinuous Kernel / G.C. Evans // Transactions of the American Mathematical Society. — 1910. — V. 11, №4. -P. 393 — 413.

8. Хромов, А.П. Интегральные операторы с ядрами, разрывными на ломаных линиях / А.П. Хромов // Математический сборник. — 2006. — T. 197, №11. — C. 115 — 142.

9. Магницкий, Н.А. Асимптотика решений интегрального уравнения Вольтерры первого рода / Н.А. Магницкий // ДАН СССР. — 1983. — T. 269, №1. — C. 29 — 32.

10. Сидоров, Н.А. Существование и построение обобщенных решений интегральных уравнений Вольтерры первого рода / Н.А. Сидоров, Д.Н. Сидоров // Дифференц. уравнения.

— 2006. — T. 42, №9. — C. 1243 — 1242.

11. Сидоров, Н.А. Нелинейные операторные уравнения с функционально возмущенным аргументом нейтрального типа / Н.А. Сидоров, А.В. Труфанов // Дифференц. уравнения.

— 2009. — T. 45, №12. — C. 1804 — 1808.

12. Сидоров, Н.А. Существование и структура решений интегро-функциональных уравнений Вольтерры первого рода / Н.А. Сидоров, А.В. Труфанов, Д.Н. Сидоров // Изв. ИГУ, сер. математика. — 2007. — T. 1. — C. 267 — 274.

13. Sidorov, N.A. Generalized solutions of Volterra integral equations of the first kind / N.A. Sidorov, M.V. Falaleev, D.N. Sidorov // Bull. Malays. Math. Soc. — 2006. — V. 29, №2. — P. 1 — 5.

14. Сидоров, Н.А. О решении операторно-интегральных уравнений Вольтерры в нерегулярном случае методом последовательных приближений / Н.А. Сидоров, Д.Н. Сидоров, А.В. Красник // Дифференциальные уравнения. — 2010. — T. 40, №6. — C. 874 — 882.

15. Сидоров, Н.А. О малых решениях нелинейных дифференциальных уравнений в окрестности точек ветвления / Н.А. Сидоров, Д.Н. Сидоров // Изв. вузов. Матем. — 2011. -№5. -C. 53 — 61.

16. Треногин, ВА. Функциональный анализ / В.А. Треногин. — Изд. 4-е. — М.: Физматлит, 2007. — 488 с.

17. Гельфонд, А.О. Исчисление конечных разностей / А.О. Гельфонд. — М.: Физматлит, 1959. — 400 с.

18. Сидоров, Д.Н. Метод монотонных мажорант в теории нелинейных уравнений Вольтерры / Д.Н. Сидоров, Н.А. Сидоров // Изв. ИГУ, сер. математика. — 2011. — T. 4, №1. —

Денис Николаевич Сидоров, кандидат физико-математических наук, с.н.с. ИСЭМ СО РАН,

доцент ИМЭИ ИГУ (Иркутск, Российская Федерация), sidorovdn@mail.ru.

MSC 93A30, 45D05, 45M05

Solution to the Volterra Integral Equations of the First Kind with Discontinuous Kernels

D.N. Sidorov, Energy Systems Institute SB RAS, Irkutsk State University (Irkutsk, Russian Federation)

The method of parametric families of continuous solutions construction for the Volterra integral equations of the first kind arising in the theory of developing systems is proposed. The kernels of these equations admit a first-order discontinuities on the monotone increasing curves. The explicit characteristic algebraic equation is constructed. In the regular case characteristic equation has no positive roots and solution of the integral equation is unique. In irregular case the characteristic equation has natural roots and the solution contains arbitrary constants. The solution can be unbounded if characteristic equation has zero root. It is shown that the number of arbitrary constants in the solution depends on the multiplicity of positive roots of the characteristic equation. We prove existence theorem for parametric families of solutions and built their asymptotics with logarithmic power polynomials. Asymptotics can be specified numerically or using the successive approximations.

Keywords: Volterra integral equation of the first kind, asymptotics, discontinuous kernel, logarithmic power polynomials, succesive approximations.

1. Sidorov D.N., Loginov B.V., Sinitsyn A.V., Falaleev M.V. Lyapunov-Schmidt Methods in Nonlinear Analysis and Applications. Dordrecht, Kluwer Academic Publishers, 2002. 548 p.

2. Sviridyuk G.A., Fedorov V.E. Linear Sobolev Type Equations and Degenerate Semigroups of Operators. Utrecht; Boston, VSP, 2003. 216 p.

3. Aparcin A.S. Neklassicheskie uravnenija Vol’terra I roda: teorija i chislennye metody [Nonclassic Volterra Integral Equations of the First Kind: Theory and Numerical Methods]. Novosibirsk, Nauka, 1999. 193 p.

4. Markova E.V., Sidler I.V., Trufanov V.V. O modeljah razvivajushihsja sistem tipa Glushkova

i ih prilozhenijah v elektroenergetike [On Modeling of Evolving Glushkov Systems and Applications in Power Industry]. Avtomatika i telemehanika, 2011, no. 7, pp. 20 — 28.