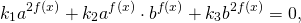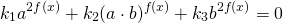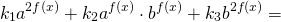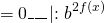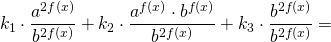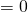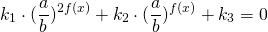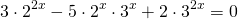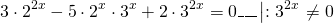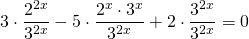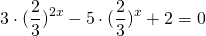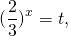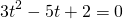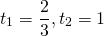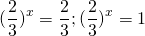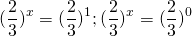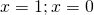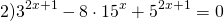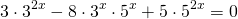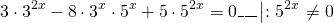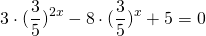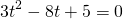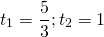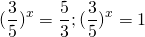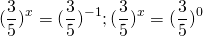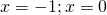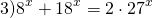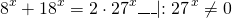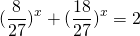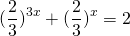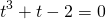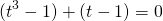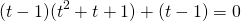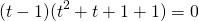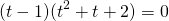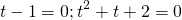Однородное показательное уравнение второй степени это

Методы решения показательных уравнений

Показательные уравнения — определение

Показательными в алгебре называют уравнения с неизвестным, которое записано в показателе степени.

Простейшее показательное уравнение в теории имеет вид:

Здесь a > 0 , a ≠ 1 .

Пример формулы простейшего показательного уравнения:

При решении показательных уравнений многие математики советуют привести их к следующему виду:

После преобразования необходимо решить уравнение:

Виды показательных уравнений

Существуют разные типы показательных уравнений, как и неравенств. К примеру, самым простым из них является:

Знак перед b определяет количество корней показательного уравнения:

• при b ≤ 0 решения отсутствуют x ∈ ∅ ;
• когда b > 0 , x = log a b .

Показательным является уравнение в кратком виде:

В этом случае, неизвестная определяется таким образом:

1. При b ≤ 0 ⇒ x ∈ ∅ .
2. При b > 0 ⇒ f x = log a b .

Показательное уравнение может быть записано таким способом:

Данное уравнение является равносильным следующему уравнению:

Другой вариант записи показательного уравнения:

φ x f x = φ x g x

В этом случае возможны следующие решения:

• при φ x = 1 все части данного уравнения являются равными для каких-либо f x , g x ;
• при φ x > 0 , φ x ≠ 1 такое уравнение равносильно уравнению f x = g x ;
• при φ x = 0 уравнение равносильно f x > 0 , g x > 0 .

Записанное показательное уравнение является равносильным совокупности систем:

φ x = 1 , x ∈ R , φ x > 0 , φ x ≠ 1 , f x = g x , φ x = 0 , f x > 0 , g x > 0 .

Существуют показательные уравнения, которые допускается привести к квадратным. Как пример:

A · a 2 x + B · a x + C = 0

В этом случае A отлично от нуля, B и C являются какими-либо числами, a>0 и не равно единице.

В процессе решения подобных показательных уравнений требуется выполнить замену:

При этом t должно быть больше нуля. Получим:

A · a f x + B · a — f x + C = 0

Здесь A, B, a являются какими-либо числами, отличными от нуля. При этом а отлично от единицы, C определяется, как произвольное действительное число. Умножим все части уравнения на a f x > 0 , чтобы свести его к квадратному уравнению:

A · a f x 2 + B + C · a f x = 0

Выполним обратную замену a f x = t , t > 0 и запишем квадратное уравнение:

A t 2 + C t + B = 0

Следующим видом показательных уравнений являются однородные.

Однородные показательные уравнения первой степени являются такими уравнениями, которые записаны в виде:

Свести подобное уравнение к показательному a f x = b несложно. Достаточно обе части равенства разделить на a f x > 0 (или b f x > 0 ) :

a f x b f x = 1 ⇒ a b f x = 1 ⇒ f x = 0

Однородным показательным уравнением второй степени называют уравнение в виде:

A · a 2 f x + B · a f x · b f x + C · b 2 f x = 0

Подобные уравнения решают, согласно стандартному алгоритму. В первую очередь следует сократить обе части уравнения на a 2 f x > 0 , либо на b 2 f x > 0 . Таким образом, выражение примет следующий вид:

A · a 2 f x + B · a f x · b f x + C · b 2 f x = 0 , : b 2 f x > 0

A · a 2 f x b 2 f x + B · a f x · b f x b 2 f x + C = 0

A · a b 2 f x + B · a b f x + C = 0

Если заменить a b f x = t , где t больше нуля, то получится квадратное уравнение:

A t 2 + B t + C = 0

Метод решения показательных уравнений через приведение к одинаковому основанию

В процессе решения показательных уравнений a x = b обычно b заменяют какой-то степенью числа а. В результате уравниваются основания. Важно правильно определить общий множитель, и решение значительно упроститься.

При идентичных основаниях, но отличающихся показателях степени, умножение чисел предполагает сложение степеней, а в процессе деления степени вычитаются.

Рассмотрим правило на примере решения показательного уравнения, содержащего корень:

Заметим, что для чисел 64 и 8 общим множителем является число 2. Запишем степени:

Подставим полученные значения и преобразуем уравнение:

( 1 2 12 ) — x = 1 2 3

1 2 — 12 x = 1 2 2 3

( 1 2 ) — 12 x = ( 1 2 ) 2 3

В результате получилась дробь.

Попробуем решить следующее показательное уравнение. Здесь будет преобразована каждая часть выражения:

( 0 , 5 ) x 2 × 4 x + 1 = 64 — 1

Вычислим, каким должно быть общее основание:

0 , 5 = 1 2 = 2 — 1

В результате получим:

( 2 — 1 ) x 2 × ( 2 2 ) x + 1 = ( 2 6 ) — 1

2 — x 2 × 2 2 x + 2 = 2 — 6

2 — x 2 2 x + 2 = 2 — 6

— x 2 + 2 x + 2 = — 6

Заметим, что для данного показательного уравнения имеется пара решений: -2 и 4

Метод решения показательных уравнений через приведение к одинаковой степени

Не всегда при решении показательных уравнений получается использовать предыдущий метод. В некоторых случаях можно упростить задачу с помощью преобразования показателей степени. Данная методика имеет место лишь в том случае, когда в выражении используются операции умножения или деления.

Умножить числа, которые отличаются основаниями, но имеют идентичные степенные показатели, можно путем умножения лишь оснований. Степень при этом не меняется:

a x b x = ( a b ) x

Потренируемся использовать записанное правило. Решим пример:

5 2 x — 4 = 49 2 — x

В этом случае можно заметить отсутствие общих множителей в обеих частях выражения. Это не позволит найти общее основание и преобразовать уравнение. Тогда поработаем с показателями:

5 2 x — 4 = 49 2 — x

5 2 x — 4 = 7 4 — 2 x

5 2 x — 4 = 1 7 2 x — 4

Закрепить принцип решения показательных уравнений с помощью приведения к одинаковой степени можно на следующем примере:

Приведем части уравнения слева и справа к одному показателю степени. С помощью свойства степенных функций преобразуем правую часть:

2 x — 2 = 1 5 x — 2

Затем следует умножить полученное выражение на 5 x — 2 :

2 x — 2 × 5 x — 2 = 1

Примеры решения показательных уравнений

Найти корни уравнения:

Заметим, что здесь b = 25 > 0 . Таким образом:

Руководствуясь свойствами логарифма, преобразуем выражение:

x = log 5 5 2 = 2 · log 5 5 = 2 · 1 = 2

x 2 x + 1 = x 3 x — 4

Заметим, что данное уравнение равносильно системе:

x = 1 , x ∈ R , x > 0 , x ≠ 1 , 2 x + 1 = 3 x — 4 , x = 0 , 2 x + 1 > 0 , 3 x — 4 > 0

⇒ x = 1 x ∈ 0 ; 1 ∪ 1 ; + ∞ , — x = — 5 , x = 0 , x > — 1 2 , x > 4 3 ⇒

⇒ x = 1 x ∈ 0 ; 1 ∪ 1 ; + ∞ , x = 5 , x = 0 , x > 4 3 ,

Ответ: x 1 = 1 , x 2 = 5

Требуется найти решения уравнения:

2 x — 3 · 4 x = 2 16 x

В первую очередь преобразуем все части равенства так, чтобы основанием было число 2:

Решим приведенное уравнение:

3 x — 3 = 1 2 — 4 x ⇒ 7 x = 7 2 ⇒ x = 1 2 .

Найти корни уравнения:

5 x — 2 · 5 x — 2 = 23

Здесь требуется вынести число 5 в самой маленькой степени, то есть в степени ( х — 2 ). В процессе разделим каждое из слагаемых на этот множитель:

5 x — 2 · 5 x — x — 2 — 2 = 23 ⇒ 5 x — 2 · 5 x — x + 2 — 2 = 23 ⇒ 5 x — 2 · 25 — 2 = 23 ⇒

⇒ 5 x — 2 · 23 = 23 ⇒ 5 x — 2 = 1

x — 2 = log 5 1 ⇒ x — 2 = 0 ⇒ x = 2

С учетом, что 1 = a 0 , уравнение 5 x — 2 = 1 допустимо записать таким образом:

5 x — 2 = 1 ⇒ 5 x — 2 = 5 0 ⇒ x — 2 = 0 ⇒ x = 2

Необходимо решить уравнение:

4 x + 1 — 3 · 2 x = 10

Здесь необходимо привести выражение к единому основанию:

4 x · 4 — 3 · 2 x — 10 = 0 ⇒ 4 · 2 2 x — 3 · 2 x — 10 = 0 ⇒ 4 · 2 x 2 — 3 · 2 x — 10 = 0

Заменим 2 x = t , при этом t больше нуля. Получим:

4 t 2 — 3 t — 10 = 0

Получилось квадратное уравнение, которое можно решить:

D = — 3 2 — 4 · 4 · — 10 = 9 + 160 = 169 = 13 2

t 1 = 3 + 13 2 · 4 = 16 8 = 2

Если выполнить обратную замену, то получится простейшее показательное уравнение 2 x = 2 :

Найти корни уравнения:

3 x + 3 2 — x = 10

3 x + 3 2 · 3 — x = 10 .

Умножим уравнение на 3 x > 0 . Получим:

3 x 2 + 9 = 10 · 3 x ⇒ 3 x 2 — 10 · 3 x + 9 = 0

Заменим 3 x = t , при этом t больше нуля. Получится квадратное уравнение:

t 2 — 10 t + 9 = 0

Согласно теореме Виета, решениями такого уравнения являются:

Выполним обратную замену:

3 x = 9 , 3 x = 1 ⇒ 3 x = 3 2 , 3 x = 3 0

Ответ: x 1 = 2 , x 2 = 0

Вычислить корни уравнения:

В этом случае целесообразно разделить уравнение, то есть все его части, на 3 x + 1 > 0 :

x + 1 = log 2 3 1 ⇒ x + 1 = 0 ⇒ x = — 1

Требуется решить уравнение:

4 x + 6 x = 2 · 9 x

В этом случае следует перенести все слагаемые в левую часть. Затем можно выполнить тождественные преобразования:

2 2 x + 2 · 3 x — 2 · 3 2 x = 0

2 x 2 + 2 x · 3 x — 2 · 3 x 2 = 0 , : 3 2 x > 0

2 3 x 2 + 2 3 x — 2 = 0

Выполним замену 2 3 x = t , где t не равно нулю. В итоге получится квадратное уравнение:

Решения данного уравнения:

t 1 = — 2 0 ∉ , t 2 = 1

Обратная замена даст нам показательное уравнение в простейшем виде:

Однородные показательные уравнения

Рассмотрим однородные показательные уравнения второй и третьей степени (1-й — здесь).

Однородное уравнение — это уравнение, все члены которого имеют одинаковую суммарную степень.

Однородные уравнения второй степени в общем виде можно записать так:

где k1, k2, k3, a и b — некоторые числа, причём a и b — положительны и отличны от единицы.

Чтобы прийти к такому виду, почти всегда уравнение требуется предварительно преобразовать. Чаще всего уравнение записывают в виде

Запишем признаки, которые позволят отличить однородное уравнение от уравнений другого вида.

Признаки однородного показательного уравнения второй степени

• уравнение содержит ровно три степени с разными основаниями;
• показатели двух степеней ровно в два раза больше показателя третьей степени;
• основание этой третьей степени равно произведению оснований двух других степеней.

Однородные показательные уравнения второй степени решаются почленным делением обеих частей на наибольшую из степеней.

0,\]» title=»Rendered by QuickLaTeX.com»/>

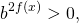
деление на степень не приводит к потере корней (то есть получаем уравнение, равносильное предыдущему).

ОДЗ: x∈R.Перепишем уравнение в виде

Разделим обе расти уравнения почтенно на 3 в степени 2x:

После упрощения приходим к уравнению

Это уравнение сводится к квадратному при помощи замены

где t>o. Оба корня квадратного уравнения

удовлетворяют условию t>0. Обратная замена

Сначала избавляемся от числовых слагаемых в показателях степеней, используя свойства степеней

представим степень с основанием 15 в виде произведения степеней с основаниями 3 и 5:

Делим обе части уравнения на 5 в степени 2x:

0,\]» title=»Rendered by QuickLaTeX.com»/>

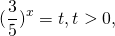
Оба корня положительны. Возвращаемся к исходной переменной:

По такому же принципу решаются однородные показательные уравнения 3-й степени.

o\]» title=»Rendered by QuickLaTeX.com»/>

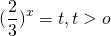
приводит к уравнению третьей степени

Представим -2=-1-1 и сгруппируем слагаемые

Общий множитель (t-1) вынесем за скобки

Получили уравнение типа «произведение равно нулю». приравниваем к нулю каждый множитель

Корень 1-го уравнения — t=1, второе уравнение не имеет корней. Обратная замена

Решение показательных уравнений

Разделы: Математика

Цели и задачи урока:

1. Знать определение показательного уравнения, определение однородного показательного уравнения второй степени.
2. Уметь решать показательные уравнения, применяя различные способы.
3. Развивать и совершенствовать умения применять имеющиеся у учащихся знания в изменяемой ситуации.
4. Воспитывать у учащихся аккуратность, культуру поведения, чувство ответственности.

Тип урока: комбинированный.

• доска, компьютер, экран, мультимедийный проектор;
• тетради, чистые листы для самостоятельной работы.

1. Организационный момент.
2. Проверка домашнего задания.
3. Подготовка учащихся к активному и сознательному усвоению нового материала.
4. Усвоение новых знаний.
5. Проверка понимания учащимися нового материала.
6. Закрепление нового материала.
7. Информация учащихся о домашнем задании.
8. Итог урока.

I. Организационный момент.

Задача: подготовить учащихся к работе на уроке.

II. Проверка домашнего задания.

Задачи: установить правильность и осознанность выполнения всеми учащимися домашнего задания; установить пробелы в знаниях; совершенствовать знания, умения и навыки в области решения показательных уравнений.

1. На экране высвечивается правильное решение домашнего задания. Ученики проверяют правильность выполнения своего решения, исправляют ошибки, задают вопросы, оценивают свое решение.

2. Всему классу предлагается устный диктант.

А) Вычислите: 2 5 ; 3 4 ; 5 3 ; ; ; 215 0 .

Б) Назвать степень числа: а) 32; б) 27; в) 625; г) 343; д) 243.

В)Какие уравнения называются показательными?

Г) Решите уравнения:

III. Подготовка учащихся к активному и сознательному усвоению нового материала.

Задача: с помощью создания проблемой ситуации подвести учащихся к новому виду показательных уравнений.

Учитель обращает внимание учеников на экран. На экране показательные уравнения. Ученикам предлагается выписать уравнения по группам.

1. Уравнения, решаемые переходом к одному основанию.
2. Уравнения, решаемые разложением на множители.
3. Уравнения, приводимые к квадратным.

1) 2 х+1 + 2 х-1 + 2 х = 28;

2) 25 х – 6*5 х + 5 = 0;

3) 6*4 х – 13*6 х + 6*9 х = 0;

4) 2 2х – 6*2 х + 8 = 0;

5) 24 х-1 + 24 х-2 – 24 х-3 = 160;

6) 0,2 х+0,5 = 5*0,04 х ;

7) 7 2х+1 + 7 2х+2 + 7 2х+3 = 57;

8) 0,4 4-5х = 0,16.

В ходе обсуждения оказалось, что только уравнение под номером 3 учащиеся не отнесли ни в одну из групп.

I V . Усвоение новых знаний.

Задачи: ввести понятие однородных показательных уравнений второй степени, познакомить учащихся со способом их решения, добиться умения определять вид однородных уравнений, отработать навыки их решения.

Учитель дает определение однородных показательных уравнений второй степени и показывает алгоритм решения таких уравнений.

А*a 2х + В*a х *b х + С*b 2х = 0

1. Так как b 2x 0, то разделим обе части уравнения на b 2x , имеем

A* + B* + C = 0

2. Введем новую переменную = t, получим квадратное уравнение At 2 + Bt + C = 0

3. Находим корни квадратного уравнения и выполняем обратную замену.

4. Решаем полученные показательные уравнения.

5. Записываем ответ.

По данному алгоритму ученики вместе с учителем решают уравнение под номером 3.

V. Проверка понимания учащимися нового материала.

Задача: установить, усвоили ли учащиеся способ решения нового вида уравнений.

На экране появляются уравнения. Ученикам предлагается назвать их вид и способ решения.

1) 2*2 2х – 3*10 х – 5*5 2х = 0;

2) 32 х+1 – 4*21 х – 7*7 2х = 0;

3) 5*3 2х + 7*15 х – 6*25 х = 0;

4) 3*49 х – 2*14 х = 2 2х .

VI. Закрепление нового материала.

Задачи: закрепить у учащихся знания и умения, которые они получили на уроке.

К доске вызываются два ученика, они решают уравнения под номерами один и два. В случае затруднения еще раз повторяют алгоритм решения однородных показательных уравнений.

Самостоятельная работа. 1 вариант решает уравнение под номером три, второй вариант – под номером четыре.

Для проверки работы ученики обмениваются листами, на экране появляется правильное решение. Ученики оценивают работу соседа.

VII. Информация учащихся о домашнем задании.

1. Повторить свойства показательной функции.
2. Повторить все изученные способы решения показательных уравнений.
3. Решить уравнения, которые ученики выписывали по группам на уроке.