Однородные и неоднородные уравнения гельмгольца

Тема 5. волновые уравнения для векторов ЭМП

Однородные и неоднородные волновые уравнения для векторов ЭМП. Уравнения Даламбера. Решение однородных уравнений Даламбера. Сферическая волна. Волновой фронт. Волновые уравнения Гельмгольца.

Плоские волны как частные решения волновых уравнений. Плоская волна как предельный случай сферической волны. Решения волновых уравнений для гармонических полей в виде плоских и сферических волн.

Плоские ЭМВ в однородной изотропной среде. Отличие понятий «волна» и «колебание». Свойства плоской волны, структура и ориентация векторов ЭМП. Коэффициенты фазы и ослабления. Длина волны. Фазовая скорость, скорость распространения энергии, групповая скорость.

Характеристическое и волновое сопротивления. Ослабление ЭМВ, глубина проникновения ЭМП в вещество.

Указания к теме

Решением волновых уравнений являются функции координат и времени, которые описывают ЭМВ, распространяющиеся в свободном пространстве, направляющих системах и других устройствах. Необходимо получить четкое представление о таких понятиях, как фазовая поверхность (волновой фронт) и ее форма, однородная и неоднородная волна, затухающая волна.

Следует выучить определения длины волны, коэффициентов затухания и фазы, групповой и фазовой скоростей, волнового и характеристического сопротивлений, глубины проникновения ЭМВ в вещество.

Основные сведения

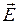
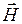
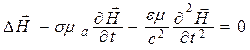
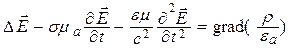
Для анализа распространяющихся ЭМВ из системы уравнений Максвелла в дифференциальной форме целесообразно вывести уравнения, которые зависят либо только от , либо только от . Если параметры среды (s, e, m) не зависят от координат и времени, то после преобразований получим [1–6]

; (5.1)

. (5.2)

Как показали расчеты и эксперименты, константа с ( 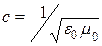) для ЭМП удивительным образом совпадает со значением скорости света в вакууме. Из этого был сделан вывод о том, что ЭМВ и свет имеют одну и ту же природу. В пространстве без потерь ЭМВ распространяются со скоростью света.

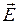
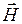
Уравнения (5.1) и (5.2) называют волновыми уравнениями Ж. Д’Аламбера [5, 12]. Если правая часть равна нулю, то уравнение называют однородным, а если нет – неоднородным. При отсутствии электрических зарядов (r = 0) уравнения (5.1) и (5.2) практически совпадают, что подтверждает равноправие векторов и у распространяющегося в пространстве ЭМП.

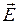
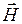
Несмотря на кажущуюся независимость уравнений (5.1) и (5.2), следует помнить о том, что у переменного ЭМП векторы и связаны уравнениями Максвелла и не могут существовать друг без друга.

Волновые уравнения в комплексной форме имеют вид

; , (5.3)

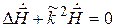
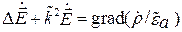
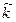
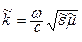
где – волновое число:

. (5.4)

Уравнения (5.3) называют волновыми уравнениями Г. Гельмгольца. При отсутствии потерь проводимости (s = 0) исчезают вторые слагаемые в уравнениях (5.1) и (5.2), а также в (5.3)–(5.4) возможно упрощение:

.

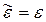
Рассмотренные уравнения называются волновыми потому, что их решениями являются волны и, в частности, ЭМВ.

Фазовым фронтом волны называют поверхность, проходящую через точки с одинаковыми фазами, по форме этой поверхности определяется название волны (сфера – сферическая ЭМВ, плоскость – плоская и т. д.) [1–3].

Решение однородного волнового уравнения для плоских волн

. (5.5)

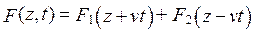
Каждое из слагаемых выражения (5.5) описывает возмущения F₁ и F₂, исходящие из точки z₀ в момент t = 0 и к моменту времени t приходящие в точку z = z₀ – vt для F₁ и в точку z = z₀ + vt для F₂ со скоростью v [1].

Для сферических волн решение волнового уравнения имеет вид:

. (5.6)

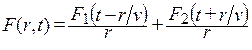
Первое слагаемое выражения (5.6) представляет собой сферическую волну, расходящуюся от источника. Второе слагаемое часто отбрасывают, поскольку волна, движущаяся внутрь источника, обычно не рассматривается [1].

В отличие от выражения (5.5) амплитуда сферической волны (5.6) уменьшается при удалении от источника как 1/r (мощность – как 1/r 2 ), что связано с тем, что мощность изотропного источника распределяется по расходящимся сферам (4.10).

Таким образом, даже при отсутствии потерь в пространстве плотность потока мощности сферической волны уменьшается с расстоянием как 1/r 2 .

На большом расстоянии от источника ЭМВ (в дальней зоне антенны) сферический волновой фронт в области приемной антенны можно аппроксимировать плоскостью, подобно тому, как земную поверхность считают плоской при малых высотах и на дистанциях, много меньших расстояния прямой видимости.

Плоская ЭМВ – идеализированная волна, имеющая плоский фазовый фронт (z = const), у которой существуют две взаимно перпендикулярные составляющие и , зависящие только от координаты z и расположенные в плоскости, перпендикулярной z. ЭМВ называется однородной, если ее амплитуда постоянна во всех точках фазового фронта, и неоднородной, если ее амплитуда зависит от координат точек фазового фронта.

В дальнейшем будем считать, что направление распространения ЭМВ совпадает с осью z. Уравнения Максвелла в комплексной форме для составляющих векторов плоской волны в ДСК имеют вид

; ; ; . (5.7)

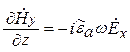
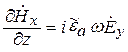
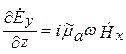
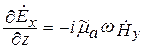
Из формул (5.7) следует, что и взаимно перпендикулярны. (Это можно доказать, рассмотрев скалярное произведение векторов [11].) В дальнейшем будем обозначать координаты этих векторов и , подчеркивая их поперечную направленность и расположение в плоскости x0y.

Зная или , можно легко найти другую поперечную составляющую и перейти к обычным координатам ( , , , ).

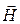
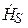
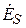
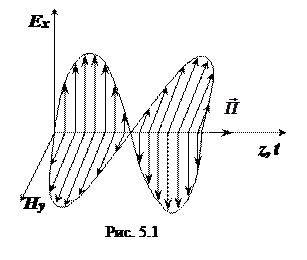
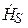
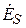
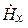
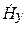
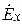
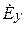
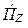
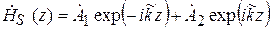
Вектор Пойнтинга в данном случае имеет только продольную составляющую (рис. 5.1). Решение уравнений (5.3) имеет вид

. (5.8)

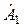
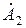
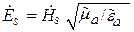
Первое слагаемое выражения (5.8) соответствует прямой волне, второе слагаемое – обратная волна, и – комплексные амплитуды данных бегущих волн (для – аналогично). Подставляя выражение (5.8) в (5.7), получим

. (5.9)

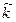
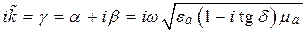
Запишем связь волнового числа ( ) с комплексным коэффициентом распространения (g) для среды без магнитных потерь :

, (5.10)

Уравнение плоской волны с учетом (5.10) можно записать в виде

. (5.11)

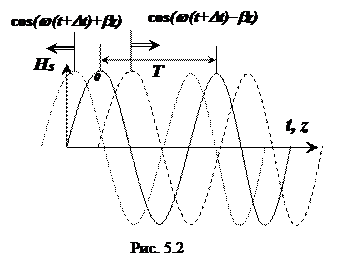
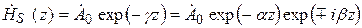
Для мгновенных значений из выражения (5.11) получаем

. (5.12)

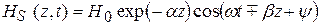
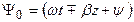
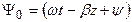
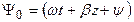
Направление распространения ЭМВ можно определить из анализа зависимости полной фазы (5.12) от времени. Зафиксировав волновой фронт в какой-то момент времени, получаем, что если , то в следующий момент времени ЭМВ сместится в положительном направлении оси z, а при волновой фронт будет двигаться в отрицательном направлении оси z(рис. 5.2) [1].

Из анализа формул (5.10)–(5.12) очевидно, что a– это коэффициент затухания, а b – коэффициент фазы.

Подставляя формулу (5.12) в (5.1), после решения уравнений относительно a и b получаем

, (5.13)

. (5.14)

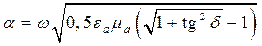
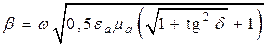
Множитель 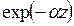в выражениях (5.10)–(5.12) показывает затухание при распространении ЭМВ вдоль оси z. Чем больше a, тем больше затухание.

Ослаблением (A) ЭМВ по полю называют величину (A_P = A 2 – ослабление ЭМВ по мощности)

, . (5.15)

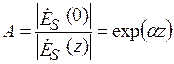
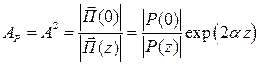
На практике часто используют ослабление в децибелах (дБ):

. (5.16)

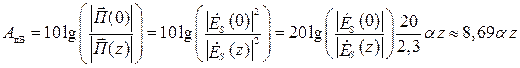
С ослаблением непосредственно связана глубина проникновения ЭМП в вещество (D° ), называемая также толщиной поверхностного слоя (скин-слоя, но это понятие логичнее использовать для металлов):

. (5.17)

При прохождении слоя вещества z =D° амплитуда ЭМП ослабляется в е (е = 2,718…) раз, и соответственно в следующий слой (рис. 5.3) проходит лишь 1/е 2 мощности ЭМП. Получается, что в поверхностном слое D° концентрируется 86,5% энергии ЭМП, в слое 2D° – 98,2%,а в слое 3D° – 99,8%.

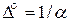
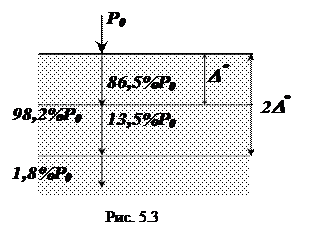
Таким образом, зная коэффициент затухания, можно определить область преимущественной концентрации энергии ЭМВ в веществе.

В случае диэлектриков толщина поверхностного слоя значительна, в то время как для проводников на ВЧ и ОВЧ она составляет доли миллиметра [1].

Параметры ЭМВ. Длиной волны l называется расстояние между двумя фронтами ЭМВ, различающимися по фазе на 2p (360°):

. (5.18)

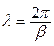
Фазовой скоростью v_ф называется скорость перемещения фазового (волнового) фронта ЭМВ. При анализе выражения (5.12) ранее были определены направление движения и скорость фронта ЭМВ

. (5.19)

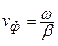
Фазовая скорость может изменяться в любых пределах (может быть больше с!), поскольку не является скоростью переноса энергии [1].

Групповой скоростью v_гр называют скорость движения фронта (например, максимума) огибающеймодулированного сигнала.

Информационный сигнал не является монохроматическим, он занимает полосу частот. Каждая спектральная составляющая может иметь свою скорость распространения, что в диспергирующих средах приводит к искажениям сигнала.

Понятие «групповая скорость» вводится для сред с малыми потерями, поэтому при Dw v_ф ( 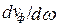>0).

При Dw/w₀ ® 0 период огибающей стремится в бесконечность, понятие «группа волн» распространяется на весь сигнал, и в итогеv_гр ® v_Э.

Групповая скорость узкополосного сигнала – это скорость передачи энергии, она не может быть выше скорости света.

Характеристическое сопротивление (Z_с) [41] ЭМВ равно отношению амплитуд поперечных составляющих электрического и магнитного полей

. (5.21)

При комплексном Z_с отстает или опережает по фазе вектор на некоторый угол. На рис. 5.5 вектор опережает на 90° (π/4), а на рис. 5.1 данные векторы синфазны.

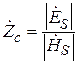
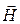
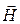
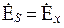
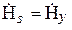
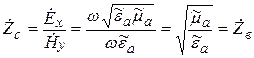
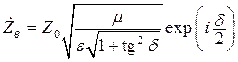
Определим характеристическое сопротивление плоской волны. Пусть , а , тогда из формул (5.7) следует:

, . (5.22)

Получается, что характеристическое сопротивление [41]зависит только от параметров среды. Z_в называют волновым сопротивлением среды. Следует отметить, что стандартом [41] рекомендуется термин «характеристическое сопротивление». Для ЭМВ, распространяющейся в некоторой среде, Z_c = Z_в.

Волновое сопротивление вакуума Z₀ (s = 0, e = m = 1) :

377,0 Ом. (5.23)

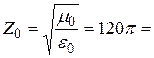
Тогда выражение (5.22) можно записать в виде

. (5.24)

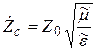
Список рекомендуемой литературы:[1, гл. 6–7, с. 30–38; 2, с. 50–56; 3, гл. 6–7, с. 27–34; 4, с. 26–33; 5, с. 26–30; 6, с. 116–123, 128–142, 198–205; 7, с. 67–82, 250–259; 8, с. 62–68; 9, с. 69–74; 10, с. 68–73; 11, с. 67–69, 130–139; 12, с. 182–194; 13, с. 140–149, 174–177, 187–190; 15, с. 302–307].

Контрольные вопросы и задания

1. Почему рассматриваемые в этой теме уравнения называются волновыми?

2. Чем волна отличается от колебания?

3. Чем отличаются волновые уравнения Д’Аламбера и Гельмгольца?

4. Следует ли из волновых уравнений независимость электрической и магнитной составляющих ЭМП?

5. Можно ли считать свет ЭМ волной?

6. Какие упрощения возможны в волновых уравнениях для сред без потерь?

7. Можно ли по виду электрической или магнитной составляющей плоской ЭМВ определить расположение другой составляющей ЭМП и направление распространения ЭМВ?

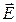
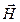
8. При каких условиях волновые уравнения для векторов и идентичны?

9. Каково простейшее решение системы уравнений Максвелла?

10. Дайте определение волнового фронта.

11. Почему плотность потока энергии сферической волны уменьшается при удалении от источника даже в пространстве без потерь?

12. Какие упрощения в анализе ЭМП дает понятие «плоская волна»? В каких практических случаях допустимо ЭМВ считать плоской?

13. Чем отличаются однородные и неоднородные плоские волны?

14. Дайте определение коэффициентам затухания и фазы плоской ЭМВ.

15. Чем отличается волновое число k от g ?

16. Какова пространственная структура плоской ЭМВ?

17. Как определить направление распространения ЭМВ?

18. Как с помощью понятия толщины поверхностного слоя можно оценить область преимущественной концентрации ЭМП?

19. Дайте определение основным характеристикам ЭМВ.

20. Чем групповая скорость отличается от фазовой?

21. Может ли фазовая скорость иметь бесконечное значение?

22. Чем волновое сопротивление отличается от характеристического?

23. Является ли групповая скорость скоростью передачи энергии?

24. Что такое дисперсия? Приведите примеры дисперсионных сред.

25. Укажите условие неискаженной передачи сигнала.

26. Чем нормальная дисперсия отличается от аномальной?

Электродинамические потенциалы гармонического поля

Раздел 5. Электродинамические потенциалы гармонического поля.

Практически все задачи электродинамики разделяют на 2 вида:

1. прямые задачи, в которых по заданному распределению сторонних источников необходимо определить соответствующее распределение электромагнитного поля.

2. обратные задачи, в которых по заданному распределению электромагнитного поля надо определить соответствующее распределение сторонних источников.

В этом разделе рассмотрим основные методы решения прямых задач электродинамики применительно для гармонического ЭМ поля и однородных линейных изотропных сред.

Относительно мгновенных значений векторов поля задачи решают очень редко, из-за сложности их определения. Обычно задачи решают для гармонических полей с использованием метода комплексных амплитуд. При решении любых электродинамических задач очень редко используют непосредственно уравнения Максвелла. Обычно уравнения Максвелла стараются свести к известным формам дифференциальных уравнений.

Рассмотрим гармонический электромагнитный процесс. Запишем уравнения Максвелла для комплексных амплитуд:

(1)

Рекомендуемые файлы

(2)

Возьмем ротор от правой и левой части соотношения (1). Получим:

(3)

Воспользуемся известным тождеством:

Из 4-ого уравнения Максвелла: следует, что:

(4)

Подставим (4) и (2) в соотношение (3) и получим: или

(5)

В результате проведенных преобразований мы получили неоднородное дифференциальное уравнение, которое в математической физике называется неоднородным уравнением Гельмгольца. Это уравнение описывает волновые процессы. Векторное дифференциальное уравнение (5) можно записать в виде трех уравнений проекций:

(6)

Аналогичные уравнения можно получить и для вектора напряженности поля.

(7)

Меняя везде знаки, получим:

(8)

При анализе сред, в которых отсутствуют сторонние источники, неоднородные уравнения (5), (8) преобразуются в однородные:

(9)

Соотношения (5), (8), (9) называются уравнениями Гельмгольца относительно векторов поля.

5.2. Электродинамические потенциалы для комплексных амплитуд.

Даже уравнения Максвелла, преобразованные к уравнениям Гельмгольца в форме (5), (8), используются при решении электродинамических задач из-за сложной правой части. При решении задач для векторов поля уравнения используются только для полей без сторонних источников. Обычно, если рассматриваемые задачи со сторонними источниками, используют искусственный прием — вводят формальные поля, которые описываются некоторыми функциями, называемыми электродинамическими потенциалами. Для них решают электродинамическую задачу, а соответствующие вектора электромагнитного поля находят, используя уравнения связи между электромагнитными потенциалами и векторами поля.

Получим выражения для электродинамических потенциалов. Для этого запишем уравнения Максвелла:

(1)

(2)

(3)

(4)

Существует следующее векторное тождество:

и (5)

Векторную функцию называют векторным электрическим потенциалом. Соотношение (5) при известном однозначно определяет вектор . Обратное определение неоднозначно, т.е. при известном векторном поле соотношение (5) определяет неоднозначно. Известно, что . Поэтому, если ввести и , то соотношение (5) не изменится. Поэтому соотношение (5) определяет с точностью до градиента произвольной функции.

Подставим (5) в (2). Получим: или (6)

Воспользуемся вновь тождеством: и .

При этом: (7)

Скалярную функцию называют скалярным электрическим потенциалом. Знак » — » поставлен, чтобы в случае электростатических полей мы получили соотношение, связывающее напряженность электрического поля и электрический потенциал. С помощью соотношений (5) и (7) определили векторы магнитного и электрического полей через два формальных поля: поля векторного электрического потенциала и поля скалярного электрического потенциала. Получим уравнения для их определения. Подставим соотношения (5) и (7) в первое уравнение Максвелла:

Помножим на , раскроем и раскроем скобки.

Формальные поля векторного и электрического потенциалов были введены без ограничений, т.е. это совершенно произвольные функции. Единственное ограничение — это то, что векторное поле электрического потенциала определяется точностью до градиента произвольной функции. Поэтому мы вправе ввести какие-то ограничения. Пусть таким ограничением будет:

(8)

Равенство (8) называется условием калибровки.

А теперь: (9)

Аналогичным образом может быть получено выражение для определения скалярного электрического потенциала. Для этого нужно воспользоваться третьим уравнением Максвелла. Вместо запишем соотношение (7):

Вместо подставим то, чему она равна, используя условие калибровки:

окончательно получаем: (10)

Таким образом, мы получили 2 уравнения: векторное дифференциальное и скалярное дифференциальное с простой правой частью. Из наших рассуждений мы можем исключить , т.е. можем свести к нахождению только . Для этого в соотношении (7) исключим , используя соотношение (8). Из соотношения (8) следует:

(11)

5.3. Решение неоднородных уравнений Гельмгольца.

Необходимо решить неоднородное уравнение Гельмгольца:

(1)

Если удастся решить это уравнение, то:

Требуется определить поле в искомой точке Р вне объема V, причем расстояние от любой точки внутри объема до точки Р значительно больше, чем размеры объема. Выделим внутри объема V точку Q и вокруг нее построим элементарный объем DV. R — расстояние между точками Q и Р. Мы ищем интенсивность поля , возбуждаемого сторонними токами в точке Р. Эта интенсивность пропорциональна (2). — некоторое среднее значение объемной плотности тока. Размеры объема значительно меньше расстояния R, поэтому с протекающими в нем сторонними токами можно рассматривать как точечный источник. В силу симметрии задачи возбуждение поля в однородном изотропном пространстве точечным источником поверхность равных фаз (фазовых фронтов) будет иметь вид сферы (сферической волны расходящейся от источника на бесконечность).

Ограничимся простым случаем: когда поле гармоническое и амплитуда поля, возбуждаемого точечным источником, зависит только от r (r – расстояние от Q до P).

(3) – постоянная распространения, т.е. среда без потерь.

где r — радиальная координата. Последнее соотношение описывает сферическую волну. Таким образом, поле, возбуждаемое этими токами в объеме DV:

(4).

Уравнения Максвелла и вытекающие из них уравнения Гельмгольца являются линейными дифференциальными уравнениями, поэтому для них справедлив принцип суперпозиции. В данном случае принцип суперпозиции истолковывается: поле, возбуждаемое элементарными объемами, находящимися внутри объема V, можно представить как суперпозицию полей, возбуждаемых сторонними токами, протекающими внутри элементарных объемов.

(5)

R_i — расстояние от V_i до точки наблюдения.

Для того чтобы возникло равенство надо определить коэффициент пропорциональности, который может быть определен в результате предельного перехода при бесконечном увеличении числа элементарных объемов в объеме V. В математической физике, при определении общего решения уравнения Гельмгольца, этот переход осуществлен:

Предположим, что у нас имеются потери: .

(6)

Когда сторонние источники распределены по поверхности S:

(7),

r — расстояние от элемента поверхности S до точки наблюдения.

Если поверхностные токи распределены по контуру, то: (8).

5.4. Уравнения Максвелла с учетом магнитных токов и зарядов.

Современная физика в настоящее время исключает возможность существования магнитных зарядов и токов, тем не менее, их введение очень упрощает решение задач.

Рассмотрим пространство, в котором существуют сторонний электрический ток и заряд. В этом случае уравнения Максвелла выглядят:

Будем предполагать, что в среде отсутствуют потери:

(1)

В рассматриваемой области, рассмотрим источники и

Уравнения Максвелла в этом случае будут:

(2)

Если в среде имеются и магнитные, и электрические источники, то уравнения Максвелла:

Из сопоставления систем (1) и (2) следует, что из любой из них может быть получена другая, если в исходной системе осуществить следующие перестановки:

(3)

Перестановки (3) получили название принципа перестановочной двойственности. Этот принцип позволяет в случае, если получено решение с одними сторонними источниками, получить готовое решение для других сторонних источников, не решая этой задачи, осуществив перестановки в соответствии с соотношением (3) в готовом решении задачи со сторонними источниками. В случае, когда имеются сторонние электрические источники, мы любую задачу решаем следующим образом:

Воспользуемся принципом перестановочной двойственности. Получим соотношения для сторонних магнитных источников:

В том случае, если в рассматриваемой задаче имеются и те, и другие источники, получаем: