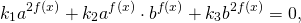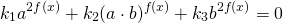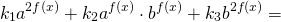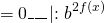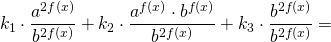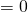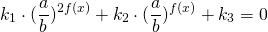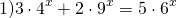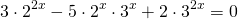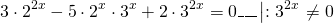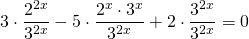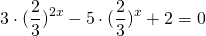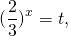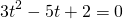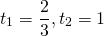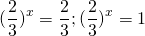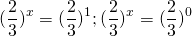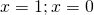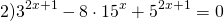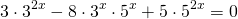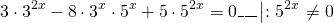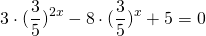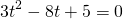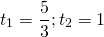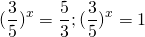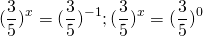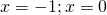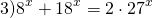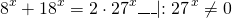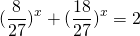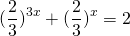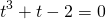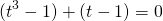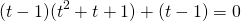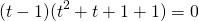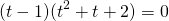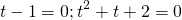Однородные показательные уравнения первого порядка

Однородные показательные уравнения

Рассмотрим однородные показательные уравнения второй и третьей степени (1-й — здесь).

Однородное уравнение — это уравнение, все члены которого имеют одинаковую суммарную степень.

Однородные уравнения второй степени в общем виде можно записать так:

где k1, k2, k3, a и b — некоторые числа, причём a и b — положительны и отличны от единицы.

Чтобы прийти к такому виду, почти всегда уравнение требуется предварительно преобразовать. Чаще всего уравнение записывают в виде

Запишем признаки, которые позволят отличить однородное уравнение от уравнений другого вида.

Признаки однородного показательного уравнения второй степени

• уравнение содержит ровно три степени с разными основаниями;
• показатели двух степеней ровно в два раза больше показателя третьей степени;
• основание этой третьей степени равно произведению оснований двух других степеней.

Однородные показательные уравнения второй степени решаются почленным делением обеих частей на наибольшую из степеней.

0,\]» title=»Rendered by QuickLaTeX.com»/>

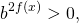
деление на степень не приводит к потере корней (то есть получаем уравнение, равносильное предыдущему).

ОДЗ: x∈R.Перепишем уравнение в виде

Разделим обе расти уравнения почтенно на 3 в степени 2x:

После упрощения приходим к уравнению

Это уравнение сводится к квадратному при помощи замены

где t>o. Оба корня квадратного уравнения

удовлетворяют условию t>0. Обратная замена

Сначала избавляемся от числовых слагаемых в показателях степеней, используя свойства степеней

представим степень с основанием 15 в виде произведения степеней с основаниями 3 и 5:

Делим обе части уравнения на 5 в степени 2x:

0,\]» title=»Rendered by QuickLaTeX.com»/>

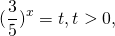
Оба корня положительны. Возвращаемся к исходной переменной:

По такому же принципу решаются однородные показательные уравнения 3-й степени.

o\]» title=»Rendered by QuickLaTeX.com»/>

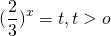
приводит к уравнению третьей степени

Представим -2=-1-1 и сгруппируем слагаемые

Общий множитель (t-1) вынесем за скобки

Получили уравнение типа «произведение равно нулю». приравниваем к нулю каждый множитель

Корень 1-го уравнения — t=1, второе уравнение не имеет корней. Обратная замена

Как решать
показательные уравнения?

Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.

Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной \(х\) не в основании степени, а в самом показателе. Как это выглядит:

Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:

Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение \(х\). Познакомиться с понятием степени и ее свойствами можно тут и тут.

И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:

И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.

Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.

Простейшие показательные уравнения

Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:

Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо \(х\) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:

Значит, если \(х=3\), то мы получим верное равенство, а значит мы решили уравнение.

Решим что-нибудь посложнее.

Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:

Мы применили свойство отрицательной степени по формуле:

Теперь наше уравнение будет выглядеть так:

Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны \(3\), только вот степени разные – слева степень \((4х-1)\), а справа \((-2)\). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:

Такое мы решать умеем, ведь это обыкновенное линейное уравнение.

Поздравляю, мы нашли корень нашего показательного уравнения.

Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что \(125=5*5*5=5^3\), а \(25=5*5=5^2\), подставим:

Воспользуемся одним из свойств степеней \((a^n)^m=a^\):

И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:

И еще один пример:

Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить \(2\) в различную степень, вы никогда не сможете получить отрицательное число.

Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.

Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.

Общий метод решения показательных уравнений

Пусть у нас есть вот такой пример:

Где \(a,b\) какие-то положительные числа. (\(a>0, \; b>0\).

Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.

Слева у нас уже стоит \(a^x\), с этим ничего делать не будем, а вот справа у нас стоит загадочное число \(b\), которое нужно попытаться представить в виде \(b=a^m\). Тогда уравнение принимает вид:

Раз основания одинаковые, то мы можем просто приравнять степени:

Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:

Замечаем, что \(16=2*2*2*2=2^4\) это степень двойки:

Основания одинаковые, значит можно приравнять степени:

$$x=4.$$
Пример 6 $$5^<-x>=125 \Rightarrow 5^<-x>=5*5*5 \Rightarrow 5^<-x>=5^3 \Rightarrow –x=3 \Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 \Rightarrow (3*3)^<4x>=3*3*3*3 \Rightarrow(3^2)^<4x>=3^4 \Rightarrow 3^<8x>=3^4 \Rightarrow 8x=4 \Rightarrow x=\frac<1><2>.$$

Здесь мы заметили, что \(9=3^2\) и \(81=3^4\) являются степенями \(3\).

Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:

\(3\) и \(2\) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число \(b>0\), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице \(a>0, \; a \neq 1\):

Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим \(2\) в виде \(3\) в какой-то степени, где \(a=3\), а \(b=2\):

Подставим данное преобразование в наш пример:

Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:

Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.

Кто забыл, что такое логарифм, можно посмотреть здесь.

Рассмотрим еще несколько аналогичных примеров.

Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:

Все эти варианты ответа верные, их можно смело писать в ответ.

И так, мы с вами научились решать любые показательные уравнения вот такого вида: \(a^x=b\), где \(a>0; \; b>0\).

Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа \(a^x=b\), где \(a>0; \; b>0\). Рассмотрим типы сложных уравнений, которые могут попасться:

Решение показательных уравнений при помощи замены

Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.

Здесь это сделать легко, замечаем, что \(9=3^2\), тогда \(9^x=(3^2)^x=3^<2x>=(3^x)^2\). Здесь мы воспользовались свойством степеней: \((a^n)^m=a^\). Подставим:

Обратим внимание, что во всем уравнении все \(х\) «входят» в одинаковую функцию — \(3^x\). Сделаем замену \(t=3^x, \; t>0\), так как показательная функция всегда положительна.

Квадратное уравнение, которое решается через дискриминант:

Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:

И второй корень:

И еще один пример на замену:

Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание \(3\). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член \(3=2+1\) и вынести общий множитель \(2\):

Подставим в исходное уравнение:

Теперь показательные функции одинаковы и можно сделать замену:

Обратная замена, и наше уравнение сводится к простейшему:

И второе значение \(t\):

Тут у нас две показательные функции с основаниями \(7\) и \(3\), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на \(3^x\):

Здесь нам придется воспользоваться свойствами степеней:

Разберем каждое слагаемое:

Теперь подставим получившееся преобразования в исходное уравнение:

Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену \(t=(\frac<7><3>)^x\):

Сделаем обратную замену:

И последний пример на замену:

Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:

Разберем каждое слагаемое нашего уравнения:

Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!

И последнее слагаемое со степенью:

Подставим все наши преобразования в исходное уравнение:

Теперь можно сделать замену \(t=2^x\) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель \(2^x\)):

Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.

И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут

Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании \(2\), \(5\) и \(10\). Очевидно, что \(10=2*5\). Воспользуемся этим и подставим в наше уравнение:

Воспользуемся формулой \((a*b)^n=a^n*b^n\):

И перекинем все показательные функции с основанием \(2\) влево, а с основанием \(5\) вправо:

Сокращаем и воспользуемся формулами \(a^n*a^m=a^\) и \(\frac=a^\):

Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.

Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!

Решение показательных уравнений

Разделы: Математика

Цели и задачи урока:

1. Знать определение показательного уравнения, определение однородного показательного уравнения второй степени.
2. Уметь решать показательные уравнения, применяя различные способы.
3. Развивать и совершенствовать умения применять имеющиеся у учащихся знания в изменяемой ситуации.
4. Воспитывать у учащихся аккуратность, культуру поведения, чувство ответственности.

Тип урока: комбинированный.

• доска, компьютер, экран, мультимедийный проектор;
• тетради, чистые листы для самостоятельной работы.

1. Организационный момент.
2. Проверка домашнего задания.
3. Подготовка учащихся к активному и сознательному усвоению нового материала.
4. Усвоение новых знаний.
5. Проверка понимания учащимися нового материала.
6. Закрепление нового материала.
7. Информация учащихся о домашнем задании.
8. Итог урока.

I. Организационный момент.

Задача: подготовить учащихся к работе на уроке.

II. Проверка домашнего задания.

Задачи: установить правильность и осознанность выполнения всеми учащимися домашнего задания; установить пробелы в знаниях; совершенствовать знания, умения и навыки в области решения показательных уравнений.

1. На экране высвечивается правильное решение домашнего задания. Ученики проверяют правильность выполнения своего решения, исправляют ошибки, задают вопросы, оценивают свое решение.

2. Всему классу предлагается устный диктант.

А) Вычислите: 2 5 ; 3 4 ; 5 3 ; ; ; 215 0 .

Б) Назвать степень числа: а) 32; б) 27; в) 625; г) 343; д) 243.

В)Какие уравнения называются показательными?

Г) Решите уравнения:

III. Подготовка учащихся к активному и сознательному усвоению нового материала.

Задача: с помощью создания проблемой ситуации подвести учащихся к новому виду показательных уравнений.

Учитель обращает внимание учеников на экран. На экране показательные уравнения. Ученикам предлагается выписать уравнения по группам.

1. Уравнения, решаемые переходом к одному основанию.
2. Уравнения, решаемые разложением на множители.
3. Уравнения, приводимые к квадратным.

1) 2 х+1 + 2 х-1 + 2 х = 28;

2) 25 х – 6*5 х + 5 = 0;

3) 6*4 х – 13*6 х + 6*9 х = 0;

4) 2 2х – 6*2 х + 8 = 0;

5) 24 х-1 + 24 х-2 – 24 х-3 = 160;

6) 0,2 х+0,5 = 5*0,04 х ;

7) 7 2х+1 + 7 2х+2 + 7 2х+3 = 57;

8) 0,4 4-5х = 0,16.

В ходе обсуждения оказалось, что только уравнение под номером 3 учащиеся не отнесли ни в одну из групп.

I V . Усвоение новых знаний.

Задачи: ввести понятие однородных показательных уравнений второй степени, познакомить учащихся со способом их решения, добиться умения определять вид однородных уравнений, отработать навыки их решения.

Учитель дает определение однородных показательных уравнений второй степени и показывает алгоритм решения таких уравнений.

А*a 2х + В*a х *b х + С*b 2х = 0

1. Так как b 2x 0, то разделим обе части уравнения на b 2x , имеем

A* + B* + C = 0

2. Введем новую переменную = t, получим квадратное уравнение At 2 + Bt + C = 0

3. Находим корни квадратного уравнения и выполняем обратную замену.

4. Решаем полученные показательные уравнения.

5. Записываем ответ.

По данному алгоритму ученики вместе с учителем решают уравнение под номером 3.

V. Проверка понимания учащимися нового материала.

Задача: установить, усвоили ли учащиеся способ решения нового вида уравнений.

На экране появляются уравнения. Ученикам предлагается назвать их вид и способ решения.

1) 2*2 2х – 3*10 х – 5*5 2х = 0;

2) 32 х+1 – 4*21 х – 7*7 2х = 0;

3) 5*3 2х + 7*15 х – 6*25 х = 0;

4) 3*49 х – 2*14 х = 2 2х .

VI. Закрепление нового материала.

Задачи: закрепить у учащихся знания и умения, которые они получили на уроке.

К доске вызываются два ученика, они решают уравнения под номерами один и два. В случае затруднения еще раз повторяют алгоритм решения однородных показательных уравнений.

Самостоятельная работа. 1 вариант решает уравнение под номером три, второй вариант – под номером четыре.

Для проверки работы ученики обмениваются листами, на экране появляется правильное решение. Ученики оценивают работу соседа.

VII. Информация учащихся о домашнем задании.

1. Повторить свойства показательной функции.
2. Повторить все изученные способы решения показательных уравнений.
3. Решить уравнения, которые ученики выписывали по группам на уроке.