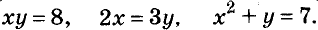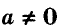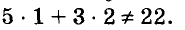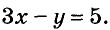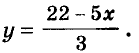Системы с нелинейными уравнениями
 Нелинейные уравнения с двумя неизвестными Нелинейные уравнения с двумя неизвестными |
 Системы из двух уравнений, одно из которых линейное Системы из двух уравнений, одно из которых линейное |
 Однородные уравнения второй степени с двумя неизвестными Однородные уравнения второй степени с двумя неизвестными |
 Системы из двух уравнений, одно из которых однородное Системы из двух уравнений, одно из которых однородное |
 Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное |
 Примеры решения систем уравнений других видов Примеры решения систем уравнений других видов |
Нелинейные уравнения с двумя неизвестными
Определение 1 . Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.
Задание числовой функции z от двух переменных x и y часто обозначают так:
| z = f (x , y) , | (1) |
причем в записи (1) числа x и y называют аргументами функции , а число z – значением функции , соответствующим паре аргументов (x ; y) .
Определение 2 . Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида
| f (x , y) = 0 , | (2) |
где f (x , y) – любая функция, отличная от функции
где a , b , c – заданные числа.
Определение 3 . Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.
Пример 1 . Решить уравнение
| x 2 – 4xy + 6y 2 – – 12 y +18 = 0 . | (3) |
Решение . Преобразуем левую часть уравнения (3):
Таким образом, уравнение (3) можно переписать в виде
| (x – 2y) 2 + 2(y – 3) 2 = 0 . | (4) |
Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений
решением которой служит пара чисел (6 ; 3) .
Пример 2 . Решить уравнение
| sin (xy) = 2 . | (5) |
вытекает, что уравнение (5) решений не имеет.
Ответ : Решений нет.
Пример 3 . Решить уравнение
| ln (x – y) = 0 . | (6) |
Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида
где y – любое число.
Системы из двух уравнений, одно из которых линейное
Определение 4 . Решением системы уравнений
называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.
Системы из двух уравнений, одно из которых линейное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 4 . Решить систему уравнений
 | (7) |
Решение . Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:
Таким образом, решениями системы (7) являются две пары чисел

Ответ : (– 1 ; 9) , (9 ; – 1)
Однородные уравнения второй степени с двумя неизвестными
Определение 5 . Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида
где a , b , c – заданные числа.
Пример 5 . Решить уравнение
| 3x 2 – 8xy + 5y 2 = 0 . | (8) |
Решение . Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле
откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):
Ответ . Решениями уравнения (8) являются все пары чисел вида
( y ; y) или
где y – любое число.
Следствие . Левую часть уравнения (8) можно разложить на множители
Системы из двух уравнений, одно из которых однородное
Системы из двух уравнений, одно из которых однородное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 6 . Решить систему уравнений
 | (9) |
рассматривая его как квадратное уравнение относительно неизвестного x :

В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение
корнями которого служат числа y1 = 2 , y2 = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .

из второго уравнения системы (9) получаем уравнение
которое корней не имеет.
Ответ : (– 2 ; 2) , (2 ; – 2)
Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
Пример 7 . Решить систему уравнений
 | (10) |
Решение . Совершим над системой (10) следующие преобразования:
- второе уравнение системы оставим без изменений;
- к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).
В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:
 | (11) |
рассматривая его как квадратное уравнение относительно неизвестного x :

В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение
которое корней не имеет.

из второго уравнения системы (11) получаем уравнение

корнями которого служат числа y1 = 3 , y2 = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .
Ответ : (– 2 ; 3) , (2 ; – 3)
Примеры решения систем уравнений других видов
Пример 8 . Решить систему уравнений (МФТИ)
Решение . Введем новые неизвестные u и v , которые выражаются через x и y по формулам:
 | (13) |
Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что
 | (14) |
Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (14) преобразуется в равносильную ей систему
из которой находим
 | (15) |
Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде
 | (16) |
У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:
Следовательно, решениями системы (16) являются две пары чисел
Из формул (13) вытекает, что 
Определение 6 . Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.
Пример 9 . Решить систему из двух уравнений с тремя неизвестными
 | (17) |
Решение . У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:
 | (18) |
Перепишем второе уравнение системы (18) в другом виде:
Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .
Ответ : (4 ; 4 ; – 4)
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».
Симметрические системы уравнений и системы, содержащие однородные уравнения
Разделы: Математика
Цели урока:
- образовательная: обучение решению систем уравнений, содержащих однородное уравнение, симметрических систем уравнений;
- развивающая: развитие мышления, внимания, памяти, умения выделять главное;
- воспитательная: развитие коммуникативных навыков.
Тип урока: урок изучения нового материала.
Используемые технологии обучения:
Оборудование: компьютер, мультимедийный проектор.
За неделю до урока учащиеся получают темы творческих заданий (по вариантам).
I вариант. Симметрические системы уравнений. Способы решения.
II вариант. Системы, содержащие однородное уравнение. Способы решения.
Каждый ученик, используя дополнительную учебную литературу, должен найти соответствующий учебный материал, подобрать систему уравнений и решить её.
По одному учащемуся от каждого варианта создают мультимедийные презентации по теме творческого задания. Учитель при необходимости проводит консультации для учащихся.
Содержание урока
I. Мотивация учебной деятельности учащихся
Вступительное слово учителя
На предыдущем уроке мы рассматривали решение систем уравнений методом замены неизвестных. Общего правила выбора новых переменных не существует. Однако, можно выделить два вида систем уравнений, когда есть разумный выбор переменных:
- симметрические системы уравнений;
- системы уравнений, одно из которых однородное.
II. Изучение нового материала
Учащиеся II варианта отчитываются о проделанной домашней работе.
1. Демонстрация слайдов мультимедийной презентации «Системы, содержащие однородное уравнение» (презентация 1).
Учащиеся записывают в тетради:
2. Работа в парах учащихся, сидящих за одной партой: учащийся II варианта объясняет соседу по парте решение системы, содержащей однородное уравнение.
Отчёт учащихся I варианта.
1. Демонстрация слайдов мультимедийной презентации «Симметрические системы уравнений» (презентация 2).
Учащиеся записывают в тетради:
2. Работа в парах учащихся, сидящих за одной партой: учащийся I варианта объясняет соседу по парте решение симметрической системы уравнений.
III. Закрепление изученного материала
Работа в группах (в группу по 4 ученика объединяются учащиеся, сидящие за соседними партами).
Каждая из 6 групп выполняет следующее задание.
Определить вид системы и решить её:
Учащиеся в группах анализируют системы, определяют их вид, затем, в ходе фронтальной работы обсуждают решения систем.
симметрическая, введем новые переменные x+y=u, xy=v
содержит однородное уравнение.
Пара чисел (0;0) не является решением системы.
IV. Контроль знаний учащихся
Самостоятельная работа по вариантам.
Решите систему уравнений:
Учащиеся сдают тетради учителю на проверку.
V. Домашнее задание
1. Выполняют все учащиеся.
Решите систему уравнений:
2.Выполняют «сильные» учащиеся.
Решите систему уравнений:
VI. Итог урока
Вопросы:
С какими видами систем уравнений вы познакомились на уроке?
Какой способ решения систем уравнений применяется при их решении?
Сообщение оценок, полученных учащимися в ходе урока.
Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
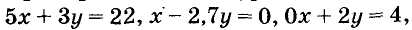
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 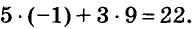
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 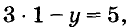
Уравнение 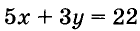
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 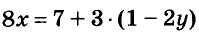
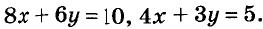
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 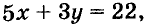
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 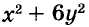
б) Значение выражения 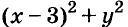
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 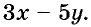
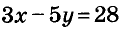
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 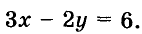
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://urok.1sept.ru/articles/512536
http://www.evkova.org/sistemyi-linejnyih-uravnenij