Огэ уравнения и неравенства с модулем

Презентация Проект «Модуль числа в заданиях ОГЭ».

В презентации приведены примеры заданий ОГЭ и ЕГЭ, при решении которых используется понятие модуля числа: уравнения и неравенства с модулями; построение графиков функций, содержащих модули; преобразование корней.

Просмотр содержимого документа
«Презентация Проект «Модуль числа в заданиях ОГЭ».»

Проект Модуль числа в заданиях ОГЭ.

Автор работы: Димитрова Алина

Руководитель проекта: Вислова М.Г.

МКОУ Краснофлотская СОШ

• закрепить навыки решения уравнений и неравенств с модулями методом интервалов;
• научиться строить графики функций с модулями;
• развить коммуникативные и общеобразовательные навыки;
• подготовиться к ОГЭ.

• Собрать и систематизировать материал по данной теме.
• Научиться решать уравнения и неравенства с модулем методом интервалов.
• Научиться строить графики функций, содержащих модули.
• Совершенствовать навыки создания презентаций и проектов.

1. Отбор задач нужного вида.

2. Поиск, отбор и систематизация теоретических сведений по теме.

3. Решение типовых задач.

4. Подборка задач данных типов и их решение.

5. Подведение итогов.

6. Создание проекта.

7. Защита проекта на уроке-конференции.

Исследование дополнительных материалов:

Я использовала интернет-ресурсы, справочники для подготовки к экзаменам и выбрала наиболее интересную и понятную информацию.

Данная тема актуальна тем, что мы являемся учениками 9 класса и нам предстоит писать ОГЭ и ЕГЭ по математике, в которые входят задания данных типов. Важно научиться грамотно это делать, чтобы быть уверенными в своих силах.

Модулем действительного числа a называется само это число, если и противоположное число – a, если a

Модулем числа называется расстояние (в единичных отрезках) от начала отсчёта до точки, изображающей это число на координатной прямой.

Термин «модуль» (от лат. modulus – мера) ввел английский математик Р.Котес (1682 – 1716), а знак модуля – немецкий математик К.Вейерштрасс (1815 – 1897) в 1841г.

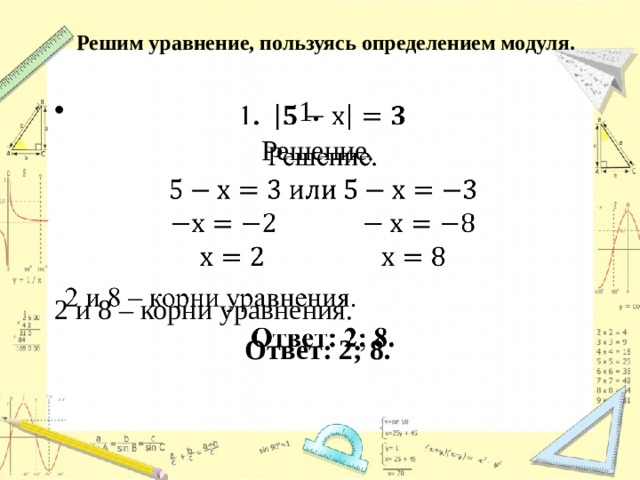
Решим уравнение, пользуясь определением модуля.

2 и 8 – корни уравнения.

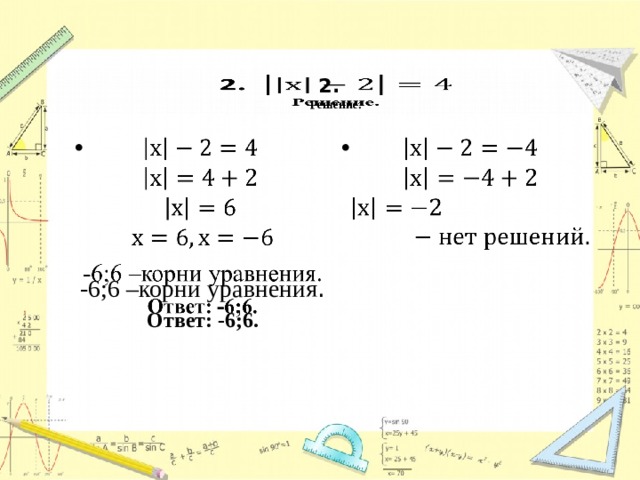
-6;6 –корни уравнения .

В правой части уравнения содержится выражение с переменной. Поэтому уравнение имеет решение при условии, что

4 – корень уравнения.

Задания для самостоятельного решения:

Метод интервалов решения уравнений и неравенств, содержащих модуль.

Рассмотрим метод интервалов на примере решения уравнения

Чтобы решить данное уравнение, необходимо раскрыть модули. Для этого выделим интервалы, на каждом из которых выражения, стоящие под знаком модуля, принимают только положительные или отрицательные значения. Отыскание таких интервалов основано на теореме:

Если на интервале (а;b) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет знак.

Чтобы выделить интервалы знакопостоянства, найдем точки, в которых выражения под знаком модуля обращаются в нуль:

х+3 = 0, х – 5 = 0, 1 – х = 0,

х = — 3, х = 5, х = 1.

Полученные точки разобьют координатную прямую на искомые интервалы:

Решим уравнение на каждом интервале.

• то

-3; — корни уравнения.

Найдем интервалы знакопостоянства:

Решим неравенство на каждом интервале.

но – 2 не принадлежит промежутку .

для любых значений

Таким образом, решением данного неравенства являюся все числа из отрезка от – 2 до 1.

Неравенства с модулями в ЕГЭ.

Модуль и преобразование корней в ОГЭ .

Понятие модуля находит применение при оперировании арифметическими корнями. Так как арифметический квадратный корень из числа может принимать только неотрицательное значение, то при записи этих значений используется модуль. В общем случае справедливо тождество :

Задания для самостоятельного решения .

Найдите значение выражения:

0. Найдем координаты вершины параболы: » width=»640″

Модуль и графики функций.

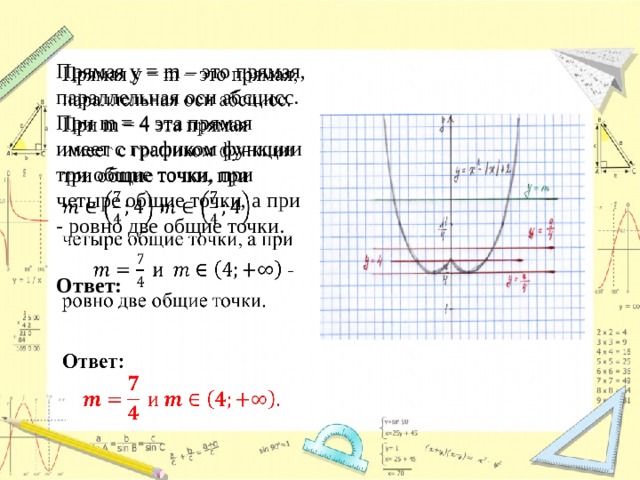
Постройте график функции и определите, при каких значениях m прямая у = m имеет с графиком ровно две общие точки.

Воспользуемся определением модуля:

• Если то Графиком функции является парабола, ветви которой направлены вверх, т.к. a 0. Найдем координаты вершины параболы:

0 . Найдем координаты вершины параболы: 3. Построим график функции: » width=»640″

2. Если то Графиком функции является парабола, ветви которой направлены вверх, т.к. a 0 . Найдем координаты вершины параболы:

3. Построим график функции:

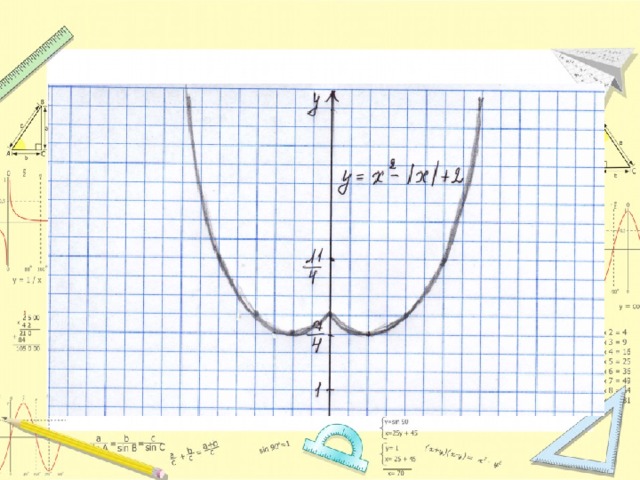
Прямая у = m – это прямая, параллельная оси абсцисс. При m = 4 эта прямая имеет с графиком функции три общие точки, при четыре общие точки, а при — ровно две общие точки.

Задания для самостоятельного решения.

• Постройте график функции Определите, при каких значениях m прямая у = m имеет с графиком ровно две общие точки.

• Постройте график функции и определите, при каких значениях m прямая у = m имеет с графиком не менее одной, но не более трех общих точек.
• Постройте график функции . Определите, при каких значениях m прямая у = m не имеет с графиком ни одной общей точки.

4. Постройте график функции

5. Постройте график функции . Определите, при каких значениях m прямая у = m имеет с графиком ровно две общие точки.

6. Постройте график функции . Определите, при каких значениях k прямая у = kx не имеет с графиком ни одной общей точки.

7. Постройте график функции Определите, при каких значениях m прямая у = m имеет с графиком ровно одну общую точку.

8. Постройте график функции Найдите наибольшее количество общих точек графика с прямой, параллельной оси абсцисс.

Уравнения с модулем

Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.

Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.

Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.

Прежде всего вспомним, что

Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)

Слева модуль, справа число

Это самый простой случай. Решим уравнение

Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:

Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.

Переменная как под модулем, так и вне модуля

Здесь приходится раскрывать модуль по определению. . . или соображать!

Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.
Ответ: 1.

Первый случай: x ≥ 3. Снимаем модуль:

Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.

Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:

Значит, больше трёх и потому является корнем исходного уравнения

Стало быть, годятся лишь и .

Ответ:

Квадратные уравнения с заменой |x| = t

Поскольку , удобно сделать замену |x| = t. Получаем:

Модуль равен модулю

Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:

Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:

Остаётся решить каждое из уравнений совокупности и записать ответ.

Два или несколько модулей

Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.

Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)

Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.

Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:

Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.

Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:

Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.

Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:

Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.

Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:

Ничего нового. Мы и так знаем, что x = 1 является решением.

Модуль в модуле

Начинаем с раскрытия внутреннего модуля.

1) x ≤ 3. Получаем:

Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.

1.1) Получаем в этом случае:

Это значение x не годится, так как не принадлежит рассматриваемому промежутку.

1.2) . Тогда:

Это значение x также не годится.

Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.

Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:

Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.

Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.

Читайте также о том, как решать неравенства с модулем.

Урок алгебры в 9-м классе (занятие элективного курса) по теме «Решение уравнений и неравенств, содержащих модули»

Презентация к уроку

На занятии изучается методика решения уравнений и неравенств, содержащих модули. Даётся подробная классификация уравнений и неравенств с модулем.

Введение. Определение модуля и его геометрический смысл.

«Модуль» (от лат. modulus-мера) ввёл английский математик Р. Котес (1682–1716). Знак модуля – немецкий математик (в 1841г.) К. Вейерштрасс (1815–1897).

Модуль числа a есть расстояние от нуля до точки a,

Модуль разности двух чисел равен расстоянию между точками числовой прямой, соответствующим этим точкам.

Используя определение модуля и его геометрический смысл, можно решить простейшие уравнения и неравенства с модулем. Простейшие уравнения и неравенства удобно решать с помощью равносильных преобразований: возведение в квадрат и т.д.

Изучение нового материала

Учитель даёт систематизацию материала, классификацию уравнений и неравенств с модулем. Показывает презентацию. Таблица №1

Таблица №1 Классификация уравнений и неравенств с модулем