Огибающая семейства кривых дифференциального уравнения

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Огибающая

Огибающая кривая

Рассмотрим семейство плоских кривых $ \left\< \mathbf K(\lambda_<>) \right\> $, зависящих от параметра $ \lambda_<> $, принимающего значения из интервала $ [a,b] \in \mathbb R_<> $. Если существует некоторая кривая $ \mathbf L_<> $, которая в каждой своей точке касается некоторой кривой рассматриваемого семейства, но при этом не совпадает ни с одной из них на протяжении какого-либо своего участка, то эта кривая $ \mathbf L_<> $ называется огибающей семейства кривых $ \left\ < \mathbf K(\lambda) \right\>$.

Пример. Для семейства окружностей (в зеленом цвете) каждая из прямых на левом рисунке считается огибающей, а составная кривая (красная) на правом — не считается:

Пусть кривые семейства $ \left\< \mathbf K(\lambda_<>) \right\> $ заданы уравнением $$ \Psi(x,y,\lambda)=0 \ , $$ где $ \Psi(x,y,\lambda_<>) $ — функция, непрерывно дифференцируемая по своим аргументам. Геометрическое место точек плоскости $ (x,y_<>) $, удовлетворяющих условиям $$ \Psi(x,y,\lambda)=0,\ \frac<\partial \Psi(x,y,\lambda)> <\partial \lambda>= 0 $$ называется дискриминантной кривой семейства $ \left\ < \mathbf K(\lambda) \right\>$.

Теорема. Дискриминантная кривая семейства включает в себя огибающую этого семейства, а также, возможно, множество особых точек — таких точек, для которых выполняются условия

Откуда взялась дискриминантная кривая? Возьмем две кривые семейства $ \mathbf K_<> $ и $ \mathbf K_ <1>$: $$ \Psi(x,y,\lambda)=0 \quad u \quad \Psi(x,y,\lambda +\Delta \lambda )=0 \ , $$ где $ \Delta \lambda_<> $ — бесконечно малая величина. Обе эти кривые должны касаться огибающей $ \mathbf L_<> $ в бесконечно близких точках $ V_<> $ и $ V_ <1>$. Рассмотрим точку $ P_<> $ пересечения этих кривых. Ее координаты должны удовлетворять обоим уравнениям, а, следовательно и уравнению $$ \frac<\Psi(x,y,\lambda + \Delta \lambda )-\Psi(x,y,\lambda)> <\Delta \lambda >= 0 \ . $$ Если устремить $ \Delta \lambda_<> $ к нулю, то, во-первых, последнее соотношение будет стремиться к $$ \frac<\partial \Psi(x,y,\lambda)> <\partial \lambda>= 0 \ , $$ а, во-вторых, точки $ P_<> $ и $ V_ <1>$ будут стремиться к точке $ V_<> $, лежащей на кривой $$ \Psi(x,y,\lambda)=0 \ . $$

Таким образом, в точке $ V_<> $ должны быть выполнены оба условия теоремы. Покажем теперь, что в этой точке касательная к дискриминантной кривой совпадает с касательной к огибаемой кривой $ \mathbf K_<> $. Для этого сделаем еще одно дополнительное предположение: будем считать, что в точке $ V_<> $ $$ \frac<\partial^2 \Psi(x,y,\lambda)> <\partial \lambda^2>\ne 0 \ . $$ Это условие гарантирует, что уравнение $$ \frac<\partial \Psi(x,y,\lambda)> <\partial \lambda>= 0 $$ задает неявную функцию $ \lambda_<> $ — как функцию $ x_<> $ и $ y_<> $: $$ \lambda = \Lambda (x,y) $$ причем эта функция будет диффренцируемой в окрестности точки $ V_<> $. Тогда для получения уравнения дискриминантной кривой достаточно подставить эту функцию в уравнение $ \Psi(x,y,\lambda)_<>=0 $: $$ \Psi(x,y,\Lambda(x,y))=0 \ . $$ В точке $ V_<> $ ее дифференциал равен: $$ \frac<\partial \Psi(x,y,\lambda)><\partial x>d\, x + \frac<\partial \Psi(x,y,\lambda)><\partial y>d\, y + \frac<\partial \Psi(x,y,\lambda)><\partial \lambda>d\, \Lambda \ . $$ Последнее слагаемое пропадает, поскольку по предположению, частная производная по $ \lambda_<> $ равна нулю. Таким образом, получившийся дифференциал функции, задающей дискриминантную кривую, совпадает в точке $ V_<> $ с дифференциалом функции $ \Psi(x,y,\lambda)_<> $, задающей огибаемую кривую. Следовательно, совпадают и касательные к этим кривым — при дополнительном предположении, что точка $ V_<> $ неособенная.

Пример. Найти огибающую семейства эллипсов

Решение. Здесь дискриминантная кривая

получается исключением параметра $ a_<> $ из системы $$ \frac+ \frac<(1-a)^2>=1,\ \frac-\frac <(1-a)^3>= 0 \ . $$ Выражаем из второго уравнения $ a_<> $: $$ a=\frac>+y^<2/3>> \ , $$ (здесь существенно ограничение $ 0 ♦

Теорема. Если функция $ \Psi(x,y,\lambda)_<> $ является полиномом относительно $ \lambda_<> $, то дискриминантная кривая задается уравнением

$$ <\mathcal D>_ <\lambda>(\Psi(x,y,\lambda)) = 0 \ . $$ Здесь дискриминант берется по переменной $ \lambda_<> $, в то время как остальные переменные считаются параметрами.

Пример. Если переписать уравнение семейства эллипсов из предыдущего примера в виде $$ (1-a)^2x^2+a^2y^2-a^2(1-a)^2=0 \quad \iff \quad -a^4+2\,a^3+(x^2+y^2-1)a^2-2\,x^2a+x^2 =0 \ , $$ то применение теоремы даст представление дискриминантной кривой: $$ -16\,x^2y^2((x^2+y^2-1)^3+27\,x^2y^2)=0 \ . $$ Случаи $ x=0 $ или $ y=0 $ соответствуют значениям параметра $ a_<> $, лежащим на границах рассматриваемого интервала. Тот факт, что оставшийся множитель определяет именно астроиду устанавливается с помощью замены переменных $ u=x^<2/3>, v=y^ <2/3>$. ♦

Пример. Семейство касательных к параболе $ y=x^2 $ задается уравнением

$$ \frac<1>=\frac <2\alpha>\quad \iff $$ $$ \alpha^2-2\,\alpha\, x+y=0 \ . $$ Здесь параметр $ \alpha_<> $ отвечает за абсциссу точки параболы. Дискриминант последнего квадратного уравнения относительно $ \alpha_<> $, приравненный нулю, дает уравнение исходной параболы. ♦

Каустика

Теория огибающих имеет важное приложение в оптике. Пусть точечный источник света расположен в точке $ \mathbf A_<> $ плоскости. Лучи света, исходящие из $ \mathbf A_<> $, падают на кривую $ \mathbf Z_<> $, которая является зеркалом, и, отражаются от нее по правилу равенства углов падения и отражения. Огибающую всех отраженных лучей называют катакаустикой 1) или фокальной линией отражения.

Теорема.Пусть точка $ \mathbf A_<> $ имеет координаты $ (x_<0>,y_0) $. Тогда уравнение прямой, на которой лежит луч, отраженный от точки $ (X,Y_<>) $ зеркала $ \mathbf Z_<> $ имеет вид: $$ T_0N+N_0T=0 \ , $$ где

Если зеркало $ \mathbf Z_<> $ задано параметрически уравнениями

$$ X= \zeta (t),\ Y= \eta (t) \ npu \ t \in [a,b] , $$ то уравнение $$ (x-\zeta)\left[2(x_0-\zeta)\zeta’ \eta’ + (y_0 -\eta)\ <(\eta')^2- (\zeta')^2\>\right]- $$ $$ -(y-\eta)\left[ 2(y_0-\eta)\zeta’ \eta’ -(x_0 -\zeta)\left\ <(\eta')^2- (\zeta')^2\right\>\right]=0 $$ определяет прямую, на которой лежит луч, отраженный от зеркала в точке $ (X,\ Y_<>) $.

Для получения огибающей этого семейства прямых нужно продифференцировать это уравнение по $ t_<> $. Два получившихся уравнения крайне громоздки и исключить из них переменную $ t_<> $ в общем случае затруднительно. Тем не менее, можно сравнительно легко найти параметрическое представление дискриминантной кривой. Дело в том, что оба уравнения являются линейными по переменным $ x_<> $ и $ y_<> $, и получившуюся систему можно разрешить — например, по формулам Крамера.

Пример. Найти катакаустику при отражении от параболы $ y=x^ <2>$ и при источнике света, расположенном в точке $ x=0,y=2_<> $.

На рисунке падающие лучи показаны желтым, отраженные — красным.

Решение. Имеем $ \zeta = t,\, \eta=t^ <2>$ и уравнение семейства отраженных прямых $$ (4\,t^4-5\,t^2+2)x+7\,yt-4\,t^5-2\,t^3-2\,t=0 \ . $$ Для нахождения уравнения огибающей данного семейства, вычисляем дискриминант этого полинома, рассматриваемого относительно переменной $ t_<> $: $$ \Phi(x,y) =784\,(16\,x^2+(4\,y-1)^2) \times $$ $$ \times \left\<8\,x^6-(1323\,y^2-1932\,y+876)x^4+ 24(637\,y^2-868\,y+340)x^2-64(7\,y-2)^3\right\>=0 \ . $$ Это уравнение определяет одну изолированную точку $ x=0_<>, y=1/4 $ (фокус параболы) и некоторую кривую, симметричную относительно оси $ <\mathbf O>y_<> $. Мы выделим только ее кусок, лежащий внутри параболы:

Теперь проиллюстрируем другой способ представления каустики — в параметрическом виде. Продифференцируем уравнение семейства по параметру $ t_<> $: $$ (16\,t^3-10\,t)x+7\,y-20\,t^4-6\,t^2-2 = 0 $$ и разрешим получившуюся систему относительно $ x_<> $ и $ y_<> $: $$ x= \frac<4\,t^3><3\,t^2-2>,\quad y =\frac<2(9\,t^4-2\,t^6-3\,t^2-2)> <7(3\,t^2-2)>\ . $$

Заметим, что если бы мы двигали источник света по оси $ <\mathbf O>y $ по направлению к фокусу параболы, то отраженные от нее лучи пересекались бы все дальше и дальше, пока не стали бы параллельными этой оси. На этом факте основано применение параболы: отражающая поверхность прожектора делается в виде параболоида вращения, в фокус которого помещается источник света. ♦

Можно и «обратить» процесс, заставив лучи, приходящие «из бесконечности» собираться в фокусе — тогда мы получаем параболическую антенну спутникового телевидения, или же боевое оружие античности, первое появление которого принято связывать с именем Архимеда.

Исторический обзор. Греческий историк Полибий описывает эпизод II Пунической войны (218-202 до н.э.) — осаду Сиракуз Марцеллом:

Согласно другому описанию хрониста Иоаннеса Цеци (конец XII века), ссылавшегося на греческого историка Диодора Сицилийского (I в. до н.э.):

По сведению греческого писателя Лукиана (II в. н.э.), Архимед построил шестиугольное зеркало, набранное из небольших шестиугольных зеркал. Каждое из них было закреплено на шарнирах и приводилось в движение цепным приводом. Благодаря этому углы поворота зеркал можно было подобрать таким образом, чтобы отраженные солнечные лучи сфокусировались в точке, находящейся на расстоянии 300 локтей (150 метров).

Во втором века до н.э. Диокл в работе «О зажигательных зеркалах» отмечал, что поверхность, являющаяся параболоидом вращения, отражает солнечные лучи в одну точку.

Эти свидетельства производили на потомков глубокие впечатления: практически все естествоиспытатели упоминали о них ( Кардано, да Винчи), или же пытались их воспроизвести. Противником легенды выступил Декарт: на основании строгого анализа, основанного на том, что Солнце нельзя считать точечным источником света, он заключил:

Авторитет Декарта был настолько высок, что зеркала Архимеда стали считаться вымыслом. Однако на защиту легенды встали ученые-практики. Первым был Чирнгауз, проводивший исследования cвойств катакаустик, образуемых параллельными лучами, отраженными от сферических вогнутых зеркал и от зеркал с меридиональным сечением в виде циклоиды. Он также изготовлял вогнутые зеркала большого диаметра и большой зажигательной силы. Самое большое вогнутое зеркало (из меди), им устроенное, имело 3 лейпцигских локтя ($ \approx 170 $ см.) в диаметре и 2 фута ($ \approx 57 $ см. (?) 2) ) фокусного расстояния; оно описано в статье

Источник.

Relatio de insignibus novi cujusdam speculi ustorii effectibus 3) («Acta Eruditorum», 1687 и 1688).

Бюффон в 1747 г. опубликовал работу «Изобретение зеркал для воспламенения предметов на больших расстояниях». Он соединил 150 отдельных отражательных зеркал и сфокусировал их в одну зону. В полдень 10 апреля 1747 года он зажег сосновую доску с расстояния 50 метров. Он был убежден, что проведение эксперимента летом позволит увеличить это расстояние вдвое.

Проведенные эксперименты возродили интерес научной общественности к катоптрике — разделу оптики, в котором изучается теория изображений, даваемых зеркально отражающими поверхностями. Дань ей отдал и Ломоносов, опубликовавший в 1741 г. «Рассуждение о катоптрико-диоптрическом зажигательном эксперименте». Инструмент Ломоносова состоял из ряда зеркал, которые направляли солнечные лучи на линзы, фокусировавших их в одну точку.

В нашу эпоху эксперименты повторялсь. 3 ноября 1973 года в заливе Кепал на территории морской базы вблизи Афин под руководством греческого инженера Сакаса 70 матросов напрявляли зеркала $ 1.7\times 0.7 $ метров на деревянную лодку, покрытую смолой, расположенную на расстоянии 55 метров. Лодка воспламенилась через 3 минуты. 15 сентября 2002 года 500 человек с помощью зеркал $ 0.45 \times 0.45 $ метров воспламенили корабельный парус на расстоянии 50 метров за несколько минут, при этом в фокусе зеркала энергия достигала 500 кВт.ч.

Источник. Часть данных для исторического обзора взяты из статьи

Стафеев С.К., Томилин М.Г. Солнечное оружие Архимеда. Машины и механизмы. 4, 2008, C. 80-87

Оригинал фотографии зеркала Чирнгауза ☞ ЗДЕСЬ

Показать несостоятельность физической модели, предложенной в произведении А.Н.Толстого:

Лучи света, падая на внутреннюю поверхность гиперболического зеркала, сходятся все в одной точке, в фокусе гиперболы. Это известно. Теперь вот что неизвестно: я помещаю в фокусе гиперболического зеркала вторую гиперболу (очерченную, так сказать, навыворот) — гиперболоид вращения, выточенный из тугоплавкого, идеально полирующегося минерала — шамонита (В), — залежи его на севере России неисчерпаемы. Что же получается с лучами?

Лучи, собираясь в фокусе зеркала (А), падают на поверхность гиперболоида (В) и отражаются от него математически параллельно, — иными словами, гиперболоид (В) концентрирует все лучи в один луч, или в «лучевой шнур» любой толщины. Переставляя микрометрическим винтом гиперболоид (В), я по желанию увеличиваю или уменьшаю толщину «лучевого шнура». Потеря его энергии при прохождении через воздух ничтожна. При этом я могу довести его (практически) до толщины иглы…

— Во время первых опытов я брал источником света несколько обычных стеариновых свечей. Путем установки гиперболоида (В) я доводил «лучевой шнур» до толщины вязальной спицы и легко разрезывал им дюймовую доску. Тогда же я понял, что вся задача – в нахождении компактных и чрезвычайно могучих источников лучевой энергии. За три года работы, стоившей жизни двоим моим помощникам, была создана вот эта угольная пирамидка. Энергия пирамидок настолько уже велика, что, помещенные в аппарат, и … зажженные (горят около пяти минут), они дают «лучевой шнур», способный в несколько секунд разрезать железнодорожный мост… Вы представляете, какие открываются возможности? В природе не существует ничего, что бы могло сопротивляться силе «лучевого шнура»… Здания, крепости, дредноуты, воздушные корабли, скалы, горы, кора земли —все пронижет, разрушит, разрежет мой луч… [5].

Пример. Катакаустика при отражении от полуокружности при источнике света, находящемся «на бесконечности»

дает представление о картинке, наблюдаемой при отражении солнечных лучей от поверхности чашки [6]:

Получим теперь формулы для каустики. Для окружности $ x=\cos t,\ y=\sin t_<> $ и источнике света, находящемся в бесконечности на оси $ \mathbf Oy $, уравнение семейства отраженных лучей имеет вид: $$x+y\operatorname 2\,t -\cos t — \operatorname 2\,t \ \sin t=0 \ . $$ Дифференцируем это равенство по $ t_<> $ и находим $ y_<> $, затем подстановкой в исходное устанавливаем $ x_<> $: $$x=\frac<1><2>\cos\,t\,(1+\cos 2\,t)=\cos^3 t ,\quad y=\frac<1><2>\sin\,t\,(2+\cos 2\,t) \ . $$ Из этих уравнений можно найти и неявное представление каустики в виде $$ [4(x^2+y^2)-1]^3-27\,x^2=0 \ . $$ Эта кривая известна как нефроида и относится к типу эпициклоид 4) . ♦

Пример. Катакаустика при отражении от окружности при источнике света, находящемся внутри нее:

Для окружности $ x^2+y^ <2>=1 $ и при $ x_<0>=0,y_0=4/5 $ имеем уравнение каустики в виде: $$-210681\,x^6+(-362043\,y^2-182520\,y+272592)x^4+ $$ $$ +(-92043\,y^4-365040\,y^3+386784\,y^2+149760\,y-80640)x^2+ $$ $$ +(13\,y+4)^3(3\,y-4)^3=0 \ . $$ При источнике на самой окружности — например, при $ x_<0>=0,y_0=1 $, — получим уравнение каустики в виде $$ 27(x^2+y^2)^2-18(x^2+y^2)-8y-1=0 \ ; $$ оно определяет замкнутую кривую

которая называется кардиоидой. ♦

Эволюта и эвольвента

Эволютой кривой $ \mathbf K $ называется огибающая семейства нормалей к этой кривой. По отношению к своей эволюте кривая $ \mathbf K $ называется эвольвентой 5) .

Теорема. Для кривой, заданной параметрически уравнениями $ X=\zeta(t), Y=\eta(t) $, представление эволюты в параметрическом виде:

Доказательство основано на общем способе построения огибающей кривой семейства: из системы линейных уравнений $$ \begin x \zeta'(t) + y \eta'(t)&=&\zeta'(t)\zeta(t) + \eta'(t) \eta(t), \\ x \zeta»(t) + y \eta»(t)&=&\zeta»(t)\zeta(t) + \eta»(t) \eta(t) +(\zeta'(t))^2+ (\eta'(t))^2. \end $$ (где первое уравнение задает семейство нормалей к кривой, а второе получается дифференцированием первого по параметру $ t_<> $) выражаются $ x_<> $ и $ y_<> $. ♦

Пример. Найти эволюту эллипса $ x^2/4+y^<2>=1 $.

Решение. Здесь $ \zeta(t)=2\cos(t),\eta(t)=\sin(t) $. Теорема дает уравнения эволюты в виде: $$ x=3/2 \cos^3(t),y=-3\sin^3(t) \quad npu \quad t\in [0, 2\pi]; $$ из них можно получить уравнение в неявном виде: $$ (2\,x)^<2/3>+y^<2/3>=3^ <2/3>\ ; $$ эта кривая оказывается уже встречавшейся нам ВЫШЕ астроидой.

Статья не закончена!

Огибающая поверхность

Рассмотрим теперь семейство $ \left\< \mathbf P(\lambda_<>) \right\> $ поверхностей в $ \mathbb R^ <3>$, зависящих от параметра $ \lambda_<> $, принимающего значения из интервала $ [a,b] \in \mathbb R $. Если существует некоторая поверхность $ \mathbf Q_<> $, которая в каждой своей точке касается некоторой поверхности рассматриваемого семейства, то эта поверхность $ \mathbf Q_<> $ называется огибающей семейства поверхностей $ \left\< \mathbf P(\lambda_<>) \right\> $.

Видим, что это определение аналогично определению огибающей кривой, за одним только исключением: в определении огибающей кривой ставится ограничение на то, что эта кривая не должна совпадать ни с одной кривой семейства на каком-то своем участке, «отрезке». А в определение огибающей поверхности аналогичного требования не приводится. На самом деле, это дополнительное ограничение должно присутствовать — хотя бы для того, чтобы отсечь случай, когда за огибающую поверхность семейства может быть взята любая поверхность этого семейства. Не буду слишком уделять внимания формальностям, считая интуитивно понятным характер ограничения, «дополняющего» определение.

Пусть поверхности семейства $ \left\< \mathbf P(\lambda_<>) \right\> $ заданы уравнением $$ \Psi(x,y,z,\lambda)=0 \ , $$ где $ \Psi(x,y,z,\lambda) $ — функция, непрерывно дифференцируемая по своим аргументам. Геометрическое место точек пространства $ (x,y_<>,z) $, удовлетворяющих условиям $$ \Psi(x,y,z,\lambda)=0,\ \frac<\partial \Psi(x,y,z,\lambda)> <\partial \lambda>= 0 $$ называется дискриминантной поверхностью семейства $ \left\< \mathbf P(\lambda_<>) \right\> $.

Пример. [2] Составить уравнение огибающей поверхности системы шаров одинаковых радиусов $ r_<> $, центры которых лежат на кривой

$$ x=\phi(\lambda), y=\chi(\lambda),z=\psi(\lambda) \, . $$ В частности, получить уравнение искомой поверхности, если центры шаров лежат на окружности $ x=R \cos \lambda, y=R \sin \lambda, z = 0 $.

Решение. Уравнение семейства шаров: $$ (x-\phi(\lambda))^2 +(y-\chi(\lambda))^2+(z-\psi(\lambda))^2-r^2=0 \ . $$ Дифференцируем это равенство по параметру $ \lambda_<> $: $$ (x-\phi(\lambda)) \phi^<\prime>(\lambda) +(y-\chi(t))\chi^<\prime>(\lambda)+(z-\psi(\lambda))\psi^<\prime>(\lambda)=0 \ . $$ Уравнение огибающей поверхности получается исключением параметра $ \lambda_<> $ из этой системы уравнений. В приведенном частном случае уравнения дискриминантной поверхности: $$ (x-R \cos \lambda)^2 + (y-R \sin \lambda)^2+z^2-r^2=0,\quad x\sin \lambda — y \cos \lambda =0 \ . $$ Исключаем $ \lambda_<> $. Из первого уравнения имеем: $$ (x^2+y^2+z^2+R^2-r^2)=2R(x \cos \lambda+ y \sin \lambda) \ . $$ Возводим в квадрат: $$ (x^2+y^2+z^2+R^2-r^2)^2=4R^2(x^2 \cos^2 \lambda+ y^2 \sin^2 \lambda+2 xy \cos \lambda \sin \lambda) \ . $$ Представим правую часть в виде $$ 4R^2(x^2 (1-\sin^2 \lambda)+ y^2 (1-\cos^2 \lambda)+2 xy \cos \lambda \sin \lambda)= 4R^2(x^2+y^2)-4R^2 (x^2\sin^2 \lambda+ y\cos^2 \lambda-2 x y\cos \lambda \sin \lambda )= $$ $$ =4R^2(x^2+y^2)-4R^2 (x\sin \lambda — y \cos \lambda)^2 \ . $$ Теперь воспользуемся вторым из уравнений, задающих дискриминантную поверхность. Уравнение огибающей поверхности: $$ (x^2+y^2+z^2+R^2-r^2)^2=4\,R^2(x^2+y^2) \ . $$ Что это за поверхность? ♦

Задачи

Источники

[1]. Бертранъ Ж. Дифференцiальное исчисленiе. СПб. Изд-во «Наука и жизнь», 1911

[3]. Рашевский П.К. Курс дифференциальной геометрии. М.Едиториал УРСС, 2003

[5]. Толстой А.Н. Гиперболоид инженера Гарина. М.Художественная литература. 1983. Текст можно найти ☞ ЗДЕСЬ

[6]. Фотография — Paul Venter; оригинал ☞ ЗДЕСЬ.

4.1. Огибающая однопараметрического семейства кривых на плоскости

Определение. Огибающей однопараметрического семейства кривых на плоскости называется кривая, которая в каждой своей точке касается одной из линий семейства.

Пусть однопараметрическое семейство кривых задается уравнением

. (4.1)

Для вычисления углового коэффициента касательной к линии семейства продифференцируем последнее уравнение по Х в предположении, что У – неявная функция от Х. Предполагаем также, что случай (особые точки семейства) из рассмотрения исключаются.

, или (4.2)

Для записи искомого уравнения огибающей формально используем ту же функцию

,

Где, однако, – произвольное аналитическое выражение. Отсюда получаем

. (4.3)

Поскольку угловые коэффициенты огибающей и касательной к линиям семейства в точке касания совпадают, то, сравнивая (4.1) и (4.2), получаем, что . Если , то , и мы получаем заданное семейство кривых. Поэтому следует считать, что . Окончательно, для определения огибающей получаем систему уравнений

, . (4.4)

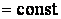
Исключая из системы параметр С, получим искомое уравнение огибающей.

Заметим, что огибающая семейства кривых может и не существовать, а исключение параметра из системы уравнений (4.4) может привести к геометрическому месту особых точек семейства, в которых кривые не имеют касательных.

Пример. Рассмотрим семейство окружностей заданного радиуса, центры которых лежат на оси ОХ:

.

Система уравнений (4.4) принимает вид

,

Что приводит к двум огибающим семейства .

Особые решения дифференциальных уравнений

Решение дифференциального уравнения

называется особым , если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция и ее частные производные и непрерывны по всем аргументам , то любое особое решение уравнения (1) удовлетворяет также уравнению

Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).

Полученное после исключения из (1) и (2) уравнение

Часто бывает так, что распадается на несколько ветвей . Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.

Пример 1. Найти особые решения дифференциального уравнения

а) Находим p-дискриминантную кривую. В данном случае и условие (2) принимает вид , отсюда . Подставляя это выражение для в уравнение (4), получаем

Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.

б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что есть решение уравнения (4).

в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде . Это уравнение Клеро. Его общее решение

Выпишем условие касания двух кривых и в точке с абсциссой :

Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой .

Полагая , находим, что условия (7) принимают вид

Подставляя в первое из равенств (8), получаем или т.е. при первое равенство выполняется тождественно, так как есть абсцисса произвольной точки.

Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой . Значит, есть особое решение уравнения (4).

г) Геометрическое истолкование.
Общее решение уравнения (4) есть семейство прямых (6), а особое решение (5) является огибающей этого семейства прямых (рис. 19).

Огибающей семейства кривых

называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые и касаются в точке , если они имеют в этой точке общую касательную.

Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения совпадают со значениями для интегральной кривой, касающейся огибающей в точке , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению , т.е. огибающая является интегральной кривой.

Далее, в каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходит, по крайней мере, две интегральные кривые: сама огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (9). Следовательно, огибающая является особой интегральной кривой.

Из курса математического анализа известно, что огибающая входит в состав C-дискриминантной кривой (коротко СДК), определяемой системой уравнений

Некоторая ветвь СДК заведомо будет огибающей, если на ней:

1) существуют ограниченные по модулю частные производные

где и — постоянные;

Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК, на которых нарушено одно из этих условий, тоже могут быть огибающими.

Пример 2. Найти особые решения дифференциального уравнения

а) Находим C-дискриминантную кривую. Имеем , так что отсюда . Подставляя это значение в (14), получаем откуда

Это и есть C-дискриминантная кривая: она состоит из двух прямых и .

б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).

в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как и , то на каждой ветви СДК имеем (предполагаем, что решение уравнения (13) рассматривается на отрезке

где — область допустимых значений .

Заметим, что на любой из ветвей СДК в области 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMRDQiiHowAFBoWFRoLFx3eb7ogAAAMZJREFUKM+1UksSwyAIVUHAX+T+p602mTYkdqZd1AUL5fk+4NzfjiQvv/QXwkz++/6kyblOYfXmMd4vNxglaF//xu0KEeJZdVYXkDFUbhaSDCDqDtDhO3ASgOypGJbMyVh4A3A8bBpQq1URM1exAEcTUHaF4R5ZzFQXDE+FuDIfET4AiqZFe+PykiQHYIbb8rAgTsAM3lvTjvc5DCVeORANFjSxbhfOqn6ux5wPICRojOf2fJ81Uscj+bmEUc5q4jKCXucmPQAaYQaRCPmIUQAAAABJRU5ErkJggg==» />, так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).

Итак, установлено, что каждое из решений (15) есть особое решение.

В вопросах отыскания особых решений оказываются полезными следующие символические схемы:

Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места точек заострения (возврата);

3) — уравнение геометрического места точек прикосновения интегральных линий, причем множитель входит в в квадрате.

Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места узловых точек, причем множитель входит в в квадрате;

3) — уравнение геометрического места точек заострения, причем множитель входит в в кубе.

Не обязательно, чтобы для каждой задачи все составные части и фигурировали в соотношениях (16) и (17).

Из всех геометрических мест только огибающая есть особое решение дифференциального уравнения. Отыскание огибающей упрощается тем, что в схемы (16) и (17) она входит в первой степени.

В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в в квадрате (и совсем не входит в ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в — в третьей, то возможно наличие геометрического места точек заострения.

Пример 3. Найти особое решение дифференциального уравнения

Решение. Особое решение, если оно существует, определяется системой

где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую , которая распадается на две ветви

Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).

Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства

являющегося общим интегралом для (18).

Выпишем систему для определения C-дискриминантной кривой откуда, исключая , получаем , или и , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии и являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.

Интегральные кривые (22) суть параболы , а линии — огибающие этого семейства парабол (рис. 20).

Пример 4. Найти особые решения дифференциального уравнения

Решение. Дифференцируем (23) по

Исключая из (23) и (24), получим . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.

Решениями уравнения (23) являются параболы и те гладкие кривые, которые можно составить из их частей (рис. 21).

Из чертежа видно, что прямая действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).

Пример 5. Найти особые решения дифференциального уравнения

Решение. Найдем . Исключая из системы уравнений получаем

Преобразовав уравнение (25) к виду , находим его общий интеграл .

Найдем . Исключая из системы уравнений будем иметь

Итак, из (26) и (27) имеем

Множитель входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что действительно удовлетворяет уравнению.

Уравнение , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения .

Наконец, уравнение , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек (рис.22).

Пример 6. Найти особые решения дифференциального уравнения

а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем , откуда

Подставляя (29) в (28), найдем уравнение :

б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде

Дифференцируя обе части (28) по и учитывая, что , будем иметь

Приравнивая нулю первый множитель , получаем (29), а соотношение дает

Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):

в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь

Подставляя (34) в (33), получаем уравнение .

Согласно символическим схемам (16) и (17) заключаем, что есть огибающая семейства полукубических парабол (33), а есть геометрическое место точек заострения (множитель входит в уравнение в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что есть решение, а решением не является (при уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).