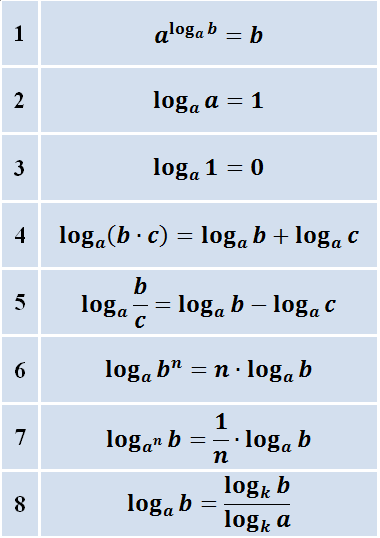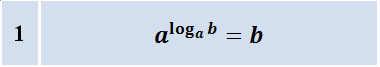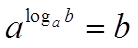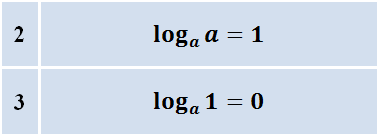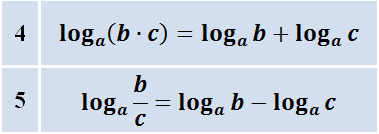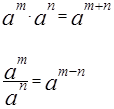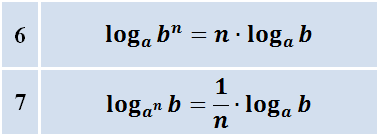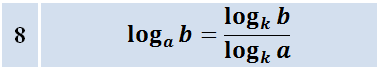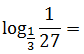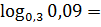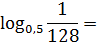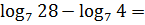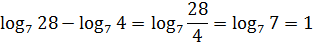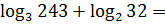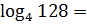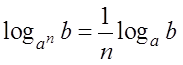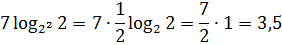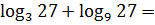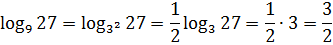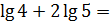Ограничение на логарифм в уравнении

Логарифмические уравнения

Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.

При этом 0,\;a> 0,\;a\neq 1′ alt=’b> 0,\;a> 0,\;a\neq 1′ />.

Обратим внимание на область допустимых значений логарифма:

Основное логарифмическое тождество:

Основные формулы для логарифмов:

(Логарифм произведения равен сумме логарифмов)

(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)

Формула перехода к новому основанию:

Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.

Все это пригодится нам в решении логарифмических уравнений.

Простейшие логарифмические уравнения

Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.

Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,\;a> 0,\;a\neq 1′ alt=’b> 0,\;a> 0,\;a\neq 1′ />.

Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.

2. Решите уравнение:

В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.

3. Решите уравнение:

Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.

4. Решите уравнение:

Область допустимых значений: 0.’ alt=’4+x> 0.’ /> Значит, -4.’ alt=’x> -4.’ />

Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом -4′ alt=’x> -4′ />.

5. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

0\\ x^<2>-4> 0\\ x^<2>+x=x^<2>-4 \end\right.\Leftrightarrow \left\ <\beginx^<2>+x> 0\\ x^<2>-4> 0\\ x=-4 \end\right.\Leftrightarrow x=-4′ alt=’\log _<8>\left ( x^<2>+x \right )=\log _<8>\left ( x^<2>-4 \right )\Leftrightarrow \left\ <\beginx^<2>+x> 0\\ x^<2>-4> 0\\ x^<2>+x=x^<2>-4 \end\right.\Leftrightarrow \left\ <\beginx^<2>+x> 0\\ x^<2>-4> 0\\ x=-4 \end\right.\Leftrightarrow x=-4′ />
Ответ: –4.

Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Запишем решение как цепочку равносильных переходов.

0 \end\right.\Leftrightarrow \left\ <\begin\left (2^<\log _<2>\left ( 4x+5 \right )> \right )^<\frac<1><2>>=9\\ x> -1\frac<1> <4>\end\right.\Leftrightarrow \left\ <\begin\left ( 4x+5 \right )^<\frac<1><2>>=9\\ x> -1\frac<1> <4>\end\right.\Leftrightarrow \left\ <\begin\sqrt<4x+5>=9\\ x> -1\frac<1> <4>\end\right.\Leftrightarrow \left\ <\begin4x+5=81\\ x> -1\frac<1> <4>\end\right.\Leftrightarrow \left\ <\beginx=19\\ x> -1\frac<1> <4>\end\right.’ alt=’2^<\log _<4>\left ( 4x+5 \right )>=9\Leftrightarrow \left\ <\begin2^\frac<<\log _<2>\left ( 4x+5 \right )>><2>=9\\ 4x+5> 0 \end\right.\Leftrightarrow \left\ <\begin\left (2^<\log _<2>\left ( 4x+5 \right )> \right )^<\frac<1><2>>=9\\ x> -1\frac<1> <4>\end\right.\Leftrightarrow \left\ <\begin\left ( 4x+5 \right )^<\frac<1><2>>=9\\ x> -1\frac<1> <4>\end\right.\Leftrightarrow \left\ <\begin\sqrt<4x+5>=9\\ x> -1\frac<1> <4>\end\right.\Leftrightarrow \left\ <\begin4x+5=81\\ x> -1\frac<1> <4>\end\right.\Leftrightarrow \left\ <\beginx=19\\ x> -1\frac<1> <4>\end\right.’ />

Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.

ОДЗ:
0\\ x> 0\\ x\neq 1 \end\right.’ alt=’\left\ <\begin12-x> 0\\ x> 0\\ x\neq 1 \end\right.’ />

Теперь можно «убрать» логарифмы.

— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′ />.

8. Решите уравнение .

ОДЗ уравнения: 0′ alt=’x> 0′ />

Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.

Вернемся к переменной х:

Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.

Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.

Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену

Вернемся к переменной х. Получим:

. Мы нашли все корни исходного уравнения.

Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.

Действия с логарифмами. Постигаем азы!

На прошлом занятии мы познакомились с понятием логарифма и порешали несколько несложных примеров на определение и смысл логарифма. Для начального знакомства.)

Теперь настал черёд более тесного знакомства с логарифмами и, соответственно, решения более серьёзных примеров. Начнём мы с ограничений в логарифмах.

Ограничения в логарифмах.

Как и у любого математического понятия, у логарифма тоже есть свои свойства и фишки. Именно о них мы сейчас и будем разговаривать. И в первую очередь это ограничения в логарифмах. До сих пор мы с вами знали лишь два жёстких ограничения в математике:

— нельзя делить на ноль;

— нельзя извлекать корень чётной степени из отрицательного числа.

С этого момента к этим двум добавляются дополнительные ограничения в логарифмах.

Для начала запишем определение логарифма в самом общем виде. Через буквы.

Напоминаю, что это равенство означает всего лишь решение показательного уравнения

А теперь подумаем, любым ли числом может быть a? Пусть, к примеру, a = 1. Тогда получается забавная штука: единица в любой степени равна единице… И каким бы ни было число c, числа a и b останутся единичками. Та же самая история и с нулём. Не подходят эти числа в качестве основания…

Отрицательные числа — очень вредные и капризные. В одну степень их можно возводить, а в другую — нельзя. Вот и поступили математики с ними, как со всеми капризными — вовсе исключили из рассмотрения.

В результате у нас получилось такое ограничение на основание:

a > 0, a ≠ 1.

А каким может быть число b? Давайте подумаем: если заведомо положительное основание a возвести любую степень c, то какое число мы в итоге получим? Верно, положительное число и получим!

Отсюда ещё одно ограничение на аргумент логарифма:

b > 0.

Вот и все ограничения. Число c (значение логарифма) может быть совершенно любым.

Конечно, при решении безобидных числовых примеров на логарифмы эти ограничения практически никак не сказываются. Зато когда столкнётесь с логарифмическими уравнениями и неравенствами, вы про эти ограничения ещё не раз вспомните! А если не вспомните, то я вам напомню. И буду напоминать при каждом удобном случае.) Ибо эти ограничения очень (!) важны при решении уравнений и неравенств. Про ОДЗ помните? Вот, то-то и оно…

Свойства логарифмов.

Итак, с ограничениями на логарифмы разобрались. Пора переходить на следующий уровень и знакомиться со свойствами логарифмов. Вот они:

Здесь всюду b>0 и c>0, а также a>0, a≠1.

Вот такой вот джентльменский набор. Ни много ни мало.) Теперь кратенько пробежимся по каждому из этих свойств. Чтобы ясно было, откуда ноги растут, как говорится.)

Начнём с первого свойства:

Обычно это свойство именуют особо — основным логарифмическим тождеством. Откуда же оно берётся? Запишем снова уже до боли знакомое нам равенство:

Из самого определения логарифма мы с вами знаем, что, если число а (основание) возвести в степень c (показатель), то получим число b:

А теперь подумаем, чему же равно у нас число c? Да вот же оно:

Подставим это выражение в предыдущее равенство и получим как раз то, что нам и требуется:

«И зачем нам такая странная перетасовка?» — спросите вы. А затем, что многоэтажное выражение превращается в элементарное b! Полезная формула.) Это единственная формула, где логарифм стоит в показателе степени.

Следующая группа формул (2-3):

Думаю, тут комментарии излишни. Всё прямо из определения логарифма следует.) И даже примеры разбирались. В предыдущем материале. Кому всё-таки непонятно, применяем старый добрый способ — словесную расшифровку. Проверено, помогает.)

Переходим к следующей группе формул (4-5):

Коротко эти формулы называются логарифм произведения и логарифм частного (дроби).

А вот с их доказательствами вопрос похитрее будет.) Эти два свойства проистекают из обычного умножения и деления степеней с одинаковым основанием. Как именно? Мы с седьмого класса помним, что при перемножении двух степеней с одинаковым основанием показатели степеней складываются, а при делении — вычитаются:

Для доказательства, например, четвёртой формулы (логарифм произведения) придётся ввести вспомогательные обозначения:

До конца доказывать эти две формулы я не буду. Как продолжить доказательство? Подставьте выражения для m и n в формулу умножения степеней и воспользуйтесь основным логарифмическим тождеством (формула №1). Попробуйте! Очень полезно.)

Кстати, прошу обратить внимание: данные формулы справедливы только при одинаковых основаниях! Если основания разные, то, скорее всего, преобразования более мудрёные…

Идём дальше. Следующая группа формул (6-7) — это формулы, позволяющие избавляться от степеней в аргументе или в основании логарифма:

Смысл их тоже прост. Если аргумент логарифма возводится в степень, то показатель степени n можно вынести наружу и приписать перед логарифмом. То же самое происходит и тогда, когда в степень возводится основание логарифма, только показатель степени переворачивается. Эти две полезные формулы избавляют нас от степеней в аргументе/основании. Если это мешает, конечно. Это понятно.)

Осталась последняя формула №8:

Это — так называемая формула перехода к новому основанию. Самая трудная для запоминания формула. Поэтому народ частенько и ленится её запоминать… А вы запомните. Не сочтите за труд.) Когда она применяется? А когда основания логарифмов — разные.) Скажем, в примере куча логарифмов по основанию 3 и затесался один логарифм по основанию 7. Его и менять надо. На тройку.) Мы с этой формулой крепко подружимся. И примеры тоже порешаем.) В соответствующем уроке.

Вот такой вот перечень формул и свойств. Их вполне достаточно, чтобы уверенно решать примеры на логарифмы любого уровня сложности. Эти формулы нужно не просто помнить, но и уметь применять. Причём в обоих направлениях — как слева направо, так и справа налево.

Ещё не помешало бы знать, что такое десятичный логарифм и что такое натуральный логарифм.

Десятичный логарифм — это просто логарифм по основанию 10:

В написании десятичного логарифма всего лишь пропадает буковка «о».

Натуральный логарифм (хотя чего уж в нём такого натурального) — это логарифм по основанию e. Иррациональному числу «e».

Что это за загадочное число, узнаете и поймёте, когда поступите в институт. В курсе матанализа.) В школьной математике это число практически не встречается, зато в высшей — сплошь и рядом.)

Обозначается натуральный логарифм вот так:

Логарифмы по этим основаниям хотя и имеют своё особое написание, но ни по определению, ни по свойствам ничем не отличаются от обычных логарифмов, скажем, по основанию два. Или три. И решаются точно так же.

Итак, будем считать, что необходимая теоретическая база подготовлена. Переходим к практике.)

Начальный уровень. Немного формул. Немного дробей. Немного степеней.

На этом уровне мы:

— впрямую используем определение логарифма,

— впрямую используем самые простые свойства логарифмов.

Мыслей здесь особых не нужно. Главное — память и внимательность. Итак, читаем, смотрим, вникаем.

Пример 1

Решение примера вытекает непосредственно из определения и смысла логарифма. В какой степени 1/3 даёт 1/27? В кубе, конечно. То есть, в третьей степени.

Пример 2

Всё то же самое, только дроби десятичные. Ну и что? Опять напрямую пользуемся определением логарифма: в какой степени 0,3 даст 0,09? В квадрате, разумеется! Или во второй степени.)

И ещё один примерчик на дроби:

Пример 3

А вот тут некоторые могут и зависнуть. Почему? Потому что связь между 0,5 и 1/128 визуально просматривается плохо. Что делать?

Что-что… Да к обычным дробям перейти! Вот вам и первый практический совет:

Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.

Этот приём, между прочим, работает не только в логарифмах, но и в других смежных темах — в показательных выражениях, в корнях.

В нашем примере 0,5 = 5/10 = 1/2. Ну и как? Связь между 1/2 и 1/128 легче углядеть? Естественно! 1/128 — это 1/2 в седьмой степени.

Что? Забыли, что 128 — это 2 в седьмой степени? Срочно повторить степени!

Пример 4

Прямое применение формулы разности логарифмов:

И как вам? Оба логарифма по отдельности ровно не считаются, зато через формулу разности — отлично!

Пример 5

А вот здесь складывать по формуле нельзя: основания разные — тройка и двойка. А формула — штука жёсткая. Раз требуются одинаковые основания, значит, так и надо.

Но тут ничего хитрого нет: оба логарифма считаются ровно.

Не каждый, правда, догадается, что 243 — это 3 в пятой степени, а 32 — это 2 в пятой… Но тут дело уже не в логарифмах, дело в степенях!

Вот вам и второй практический совет.

Степени популярных чисел надо знать. В лицо!

Конечно, возвести двойку в седьмую степень или тройку в пятую может каждый. Не в уме, так хотя бы на черновике. Но это умение слабо помогает в работе с логарифмами, да. А вот сообразить, какое число и в какой степени скрывается за числом 128 или 243 — это уже совсем другое дело. Почувствуйте разницу, что называется!

Поскольку умение распознавать степени в лицо пригодится не только на этом уровне, но и на следующих, вот вам небольшое задание:

Определить, какими степенями и каких чисел являются числа:

4; 8; 16; 27; 32; 36; 49; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729; 1024.

Ответы (вразброс, естественно):

27 2 ; 2 10 ; 3 6 ; 7 2 ; 2 6 ; 9 2 ; 3 4 ; 4 3 ; 10 2 ; 2 5 ; 3 5 ; 7 3 ; 16 2 ; 2 7 ; 5 3 ; 2 8 ; 6 2 ; 3 3 ; 2 9 ; 2 4 ; 2 2 ; 4 5 ; 25 2 ; 4 4 ; 6 3 ; 8 2 ; 9 3 .

Да-да! Не удивляйтесь, что ответов побольше, чем заданий. Например, 2 8 , 4 4 и 16 2 — это всё 256.

А теперь я настоятельно рекомендую взять любой учебник по школьной математике и порешать оттуда простейшие примеры на логарифмы. Порешали? Хоть что-то получилось? Тогда будем считать, что начальный уровень вы прошли. Переходим на следующий уровень.

Почти все формулы. Почти все степени. Поиск «братьев по степени».

На этом уровне применяем почти все формулы работы с логарифмами. Кроме последней формулы перехода к новому основанию. А также закрепляем наши навыки работы со степенями.

Поехали расширять наши возможности!

Пример 6

Вот тут прямое применение определения логарифма не годится: из четвёрки 128 простым возведением в степень никак не сделаешь. И формулы логарифмов непонятно как употреблять… Не беспокойтесь, сейчас всё получится.) При маленьком условии, что вы узнали в лицо число 128. Да! Это 2 в седьмой степени! Так и запишем:

Вот и одна из формул (третья снизу) приходит на помощь. Та, где показатель степени ставится множителем перед логарифмом:

Вот и выносим семёрку за наш логарифм. Пишем:

Что дальше? Дальше осталось вспомнить, что 4 = 2 2 . Верно!

Вот и ещё одна формулка в дело просится!) Вторая снизу, где в степень возводится основание логарифма. Только в этом случае при вынесении показателя наружу его надо перевернуть: 1/n.

Вот так вот! А если бы мы не узнали в числе 128 степень двойки, то так и застряли бы на этом, в общем-то несложном примере…

А теперь мы вплотную подошли к одному весьма и весьма полезному приёму в работе с логарифмическими и показательными выражениями. Приём этот называется «поиск братьев». Братьев по степени. И по разуму тоже.) Суть этого полезного приёма заключается в тщательном осмотре примера и распознавании одного и того же числа в разных степенях.

Этот приём (шифровка одного и того же числа в разных степенях) — очень популярный приём в логарифмах! Да и в показательных уравнениях и неравенствах тоже. Например, числа 27 и 243 — родные братья! Да, 243 из 27 прямым возведением в натуральную степень никак не получить, но зато они — родня по тройке! Так как 27 = 3 3 , а 243 = 3 5 . В разобранном только что примере родственниками оказались 4 и 128. По числу 2. В общем, идея понятна, да?

И зачем всё это нужно — распознавать степени и родственников? А затем, что примеры от этого проще становятся! И формулы свойств логарифмов сразу высвечиваются.) Особенно важно получить в примере одинаковые основания у логарифмов, ибо чем больше одинаковых значков в примере и меньше разных, тем лучше. И не нужно здесь применять формулу перехода к новому основанию: зачем же из пушки по воробьям палить.?)

Следующий пример на братьев (или сестёр):

Пример 7

В примере стоит сумма логарифмов, но основания логарифмов разные — тройка и девятка. Стало быть, применять напролом формулу суммы логарифмов нельзя. Но! Первый логарифм уже считается ровно, получится просто тройка:

А со вторым логарифмом что? Из девятки 27 возведением в целую степень не получишь! Но зато 9 и 27 — родня! По тройке.) Самое время вспомнить, что:

Что ж, поработаем отдельно со вторым логарифмом. Перейдём в основании от девятки к тройке. Поможет нам такое преобразование или нет — неизвестно. Но что-то делать всё-таки надо, правда? Итак, преобразовываем второй логарифм по второй (снизу) формуле — выносим степень из основания за логарифм:

Осталось лишь сложить 3 (первый логарифм) и 3/2 (второй логарифм)

Так, с близкой роднёй разобрались. Идём дальше. Иногда пример может не соответствовать в точности формуле, а может быть лишь похожим на одну из формул. И наша задача — сначала преобразовать пример под ту или иную формулу. Как, например, этот:

Пример 8

Напоминаю, что запись lg означает просто логарифм по основанию 10. И всё.)

Итак, основания логарифмов уже одинаковые — десятка. Ну прям напрашивается формула суммы логарифмов! А н-е-ет, не катит! Двойка во втором слагаемом всё портит. Коэффициент, понимаешь.) А формула применима только к чистым логарифмам, безо всяких коэффициентов. Но горевать рано! Мы эту двойку сейчас ликвидируем. Безопасно для примера.) Мы её внутрь логарифма загоним. Как? Всё по той же формуле логарифма от степени:

Здесь как раз тот случай, когда формулу надо применять справа налево. Ни в одной другой теме школьной математики нельзя вот так красиво избавляться от мешающих коэффициентов, а в логарифмах — пожалуйста! Итак, избавляемся от двойки перед вторым логарифмом:

Вот так. Осталось лишь сложить два логарифма по формуле логарифма произведения (опять же в применении справа налево). Вот и складываем:

lg4 + lg25 = lg(4́·25) = lg100 = 2

Напоминаю, что десятичные логарифмы формулу ничуть не портят, ибо они по своим свойствам ничем не отличаются от обычных!

Вот вам и третий практический совет.

Любую степень можно записать множителем перед логарифмом. И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.

Ну что, вот и состоялась наше более близкое знакомство с логарифмами! Осталось теперь с ними крепко подружиться. На следующем уровне и в следующем уроке.)

Традиционные примеры для самостоятельного решения.

Алгебра

План урока:

Понятие логарифма

Великий ученый Пьер-Симон Лаплас говорил, что изобретение логарифмов продлило жизнь астрономов вдвое, ведь с их помощью астрономические расчеты, которые ранее занимали несколько месяцев, стало возможно выполнять за считанные дни. Что же представляют собой логарифмы и как они так сильно упрощают вычисления? Для ответа на этот вопрос сначала следует вспомнить показательные уравнения.

Рассмотрим простейшее показательное уравнение 2 х = 4. Так как 2 2 =4, то, очевидно, оно имеет единственный корень, равный 2. Найти его можно не только аналитически, но и графически:

Далее посмотрим на уравнение 2 х = 8. Так как восьмерка – это двойка в кубе (2 3 = 8), то единственным корнем ур-ния будет число 3. Также проиллюстрируем это с помощью графика:

Однако если мы попытаемся решить уравнение 2 х = 6, то мы столкнемся с проблемами. Представить шестерку как какую-то степень двойки не получается. Графический метод показывает, что у этого ур-ния есть единственный корень, который лежит между числами 2 и 3, но точно определить его значение не получается:

Можно доказать (мы не будем этого делать), что искомый нами корень невозможно выразить с помощью дробей и даже корней n-ой степени. Поэтому возникает необходимость ввести какое-то новое обозначение, чтобы записывать корни таких уравнений. Математики придумали для такого числа обозначение log₂ 6, которое читается как «логарифм шести по основанию два».

Рассмотрим теперь более общий случай. Пусть есть некоторое ур-ние

Если число b положительно, то уравнение имеет корень, и при том единственный. Для его обозначения используется запись log_ab. Покажем, как графически показать значение величины log_ab. Для этого надо построить показательную функцию у = а х и горизонтальную линию у = b. Они пересекутся в единственной точке (если b положительно). Абсцисса (координата х) этой точки и будет равна log_ab:

Дадим строгое определение логарифма:

Задание. Какое число является решением показательного уравнения

Задача. Слиток радиоактивного изотопа, чей период полураспада (его обозначают буквой Т) составляет 10 минут, имеет начальную массу (m₀), равную 1 кг. Через сколько минут его вес уменьшится до 300 грамм (0,3 кг)? Масса радиоактивного изотопа изменяется по закону

m(t) = m₀•2 – t/ T

Решение. Подставим исходные данные в формулу, и получим уравнение с неизвестной величиной t:

Получили простейшее показательное уравнение, однако его левую часть (число 0,3) нельзя представить как степень двойки. Однако с помощью определения логарифма мы можем записать, что

Умножаем ур-ние на (– 10) и получаем:

С помощью калькулятора или компьютера можно узнать, что

Тогда искомое нами время примерно равно

t = – 10 log₂ 0,3 ≈ – 10•(– 1,737) ≈ 17,37 минут ≈ 17 минут 22 секунды

Ответ: – 10 log₂ 0,3 минут ≈ 17 минут 22 секунды.

Из задачи видно, что с логарифмы используются и при решении некоторых практических задач.

Иногда бывает удобнее использовать иное определение, которое по своей сути почти не отличается от первого:

Вычислим для примера несколько простейших логарифмов:

Ограничения, связанные с логарифмом

Заметим, что сам логарифм может оказаться любым вещественным числом, ведь мы умеем возводить числа и в отрицательные, и в дробные, и даже в иррациональные степени. Однако для логарифма log_ab некоторые ограничения накладываются на значение числа а (оно называется основанием логарифма) и на значение числа b (будем называть его аргументом логарифма).

Напомним, что при определении показательной функции у = а х было введено ограничение, согласно которому основание степени (число а) должно быть строго положительным числом и при этом НЕ может равняться единице. Из-за этого и основание логарифма должно также соответствовать этому ограничению. Основание логарифма и основание показательной функции даже специально обозначают одной буквой а, чтобы связь этих двух понятий была очевидней.

Также напомним, что показательное уравнение а х = b имеет решение только при положительных значениях b. Это решение и представляет собой log_ab. Если же число b отрицательно, то корня у уравнения нет, а значит и вычислить log_ab невозможно. Поэтому аргумент логарифма не может быть отрицательным.

Сформулируем эти ограничения в виде одного правила:

Ранее мы уже сталкивались с тремя случаями, когда выражения не имеют смысла. Во-первых, это происходит при делении на ноль (или нахождении нуля в знаменателе дроби, что, по сути, одно и то же). Во-вторых, выражения бессмысленны, если под корнем четной степени находится отрицательное число. В-третьих, не имеют смысла выражения, в которых отрицательные числа возводятся в дробную степень, ведь возведение в дробную степень можно заменить извлечением корня

а отрицательное число не должно оказываться под знаком корня

Сейчас мы узнали четвертый подобный случай, связанный с понятием логарифма. Больше в рамках школьного не будут рассматриваться никакие другие ситуации, в которых выражение может потерять смысл.

Основные свойства логарифмов

Любое число, возведенной в первую степень, равно самому себе. То есть справедливо равенство

Из него, пользуясь определением логарифма, получаем первое важное его свойство: log_аa = 1.

Продемонстрируем использование этого правила:

Любое число при возведении в нулевую степень равно единице:

Из этого следует второе важное правило: логарифм единицы по любому основанию равен нулю:

Покажем несколько примеров использования этого тривиального правила:

Для получения третьего свойства логарифма запишем очевидно справедливое равенство:

Пользуясь определением логарифма, мы можем записать, что log_aa c = c.

Продемонстрируем, как работает это свойство логарифмов:

Это правило можно применить для вычисления некоторых простейших логарифмов:

Логарифм log_ab, согласно одному из своих определений, это та степень, в которую нужно возвести а, чтобы получилось b. Это определение можно представить в виде формулы:

Данное равенство называют основным логарифмическим тождеством.

В силу этого тождества справедливы следующие равенства:

Функция логарифма

Арифметическое действие, в ходе которого находят логарифм какого-либо числа, называется логарифмированием. Это действие является обратным по отношению к возведению в степень. Проиллюстрируем это табличкой, в которой слева будет показана операция возведения в степень, а справа – логарифмирование:

Теперь подумаем о функции у = log_ax. Так как логарифмирование является обратным действием для возведения в степень, то и ф-ция у = log_ax должна быть обратной для показательной ф-ции у = а х .

В свою очередь это означает, что графики этих двух функций должны быть симметричны относительно прямой, задаваемой уравнением у = х.

Напомним, что на вид показательной функции у = а х влияет значение основания степени а. Если оно больше единицы, то функция оказывается возрастающей. Тогда и обратная ей логарифмическая функция также окажется возрастающей. Для примера построим графики у = 2 х и у = log₂x.

Полученный график логарифмической функции называют логарифмической кривой, однако понятно, что она представляет собой всё ту же экспоненту, которую отобразили симметрично относительно оси Ох.

График у = log₂x можно и построить иначе, по точкам, просто вычислив ее значение в нескольких «удобных» для вычисления точках:

Видно, что в обоих случаях получился один и тот же график. Похожим будет и график любой функции у =log_ax, если число а будет больше единицы.

Ситуация меняется в том случае, когда а х будет убывающей. Тогда убывающим окажется и логарифмическая функция. Для примера построим график ф-ции = 0,5 х и график обратной ей функции у = log_0,5x:

Возможно, вы заметили, что графики у = log₂x и у = log_0,5xчем-то похожи друг на друга. И действительно, если построить их на одной плоскости, то мы увидим, что они симметричны относительно оси Ох:

Причиной такой симметрии является то, что их основания, числа 2 и 0,5, являются обратными числами, то есть при перемножении дают единицу (2•0,5 = 1).

Аналогично такой же симметрией будут обладать любые две логарифмические кривые с обратными основаниями. Это свойство логарифмов мы докажем чуть позднее.

Далее построим ещё несколько графиков, чтобы лучше понять свойства логарифмических функции:

Анализируя полученные графики, мы можем заметить следующие свойства функции логарифма:

Область определения логарифмической функции – это множество всех положительных чисел, то есть промежуток (0; + ∞). Действительно, выражение log_аb имеет смысл только тогда, когда число b> 0.

Областью значения логарифмической функции является множество всех действительных чисел, то есть промежуток(– ∞; + ∞).

Логарифмическая функция является строго монотонной. При этом при основании а > 1 она возрастает, а при основании 0

График каждой логарифмической функции проходит через точку (1; 0). Это связано с тем, что для любого основания справедливо равенство log_a 1 = 0.

Три основных вида логарифмов

Математика изучает логарифмы с любыми положительными основаниями. Однако на практике наиболее распространены три их вида.

Первым из них является десятичный логарифм, основание которого равно 10. Дело в том, что его помощью до изобретения калькуляторов и компьютеров можно было быстро и с высокой точностью перемножать большие числа, используя такой прибор, как логарифмическая линейка. История понятия логарифма начиналась в XVI-XVII веках и была связана именно с необходимостью выполнения сложных арифметических действий с большими числами. Для обозначения десятичных логарифмов используют специальный символ lg, то есть

Сегодня из-за развития электроники десятичные логарифмы используются значительно реже по сравнению с 50-60 г. XX века. Но, так как почти вся вычислительная техника построена на использовании двоичной системы счета, возросла значимость двоичного логарифма log₂b. Для его обозначения не используются никакие специальные символы, однако в работах, посвященным информатике и оценке сложности алгоритмов, он используется особенно часто.

Наконец, самым важным является натуральный логарифм. Это логарифм, основанием которого является число e, примерно равное 2,71828… Для его обозначения используют символ ln, то есть

Свойства натурального логарифма, которые отличают его от других логарифмов, будут изучены нами позднее, в 11 классе. Заметим лишь, что многие физические формулы содержат именно натуральный логарифм.

Преобразования логарифмических выражений

Для работы с логарифмическими выражениями надо знать несколько основных свойств логарифмов. Первое из них помогает вычислять логарифм произведения.

Для доказательства этого правила введем обозначения. Пусть

Тогда нам надо доказать, что z = x + у. По определению логарифма мы можем записать что

Теперь подставим (1) и (2) в (3):

Получили, что a z = a x + y . В этом равенстве в обеих частях стоят степени с совпадающим основанием а. Значит, должны совпадать и их степени, то есть

что и мы и пытались доказать.

Убедимся в справедливости этого правила на простейшем примере. Очевидно, что

log₂ 4 = 2, ведь 2 2 = 4

log₂ 8 = 3, ведь 2 3 = 8

log₂ 32 = 5, ведь 2 5 = 32

С одной стороны, так как

С другой стороны, число 32 можно представить как произведение 4•8, то есть

С учетом этого получаем, что

Покажем несколько примеров использования только что доказанного правила:

Отдельно отметить, что правило сложения логарифмов действует и в том случае, когда складываются не два, а большее количество логарифмов:

Второе правило используют для определения логарифма от степени какого-либо числа.

Грубо говоря, показатель степени можно перенести и записать перед знаком логарифма. Сначала для наглядности приведем доказательство только для случая, когда r– целая степень. Тогда число b r можно представить как произведение r множителей, равных b. Однако логарифм такого произведения можно заменить на сумму r логарифмов:

Однако более строгое доказательство должно рассматривать и случай, когда r – это отрицательное или даже дробное число. Поэтому, как и в ситуации с доказательством первого правила, введем переменные. Пусть

Получается, что нам доказать, что у = r•x. Из определения логарифма следуют следующие формулы:

Подставляя первую формулу во вторую, получаем:

И снова, если у двух равных степеней равны основания, то и показатели обязательно будут равными:

Это равенство мы и пытались доказать.

Продемонстрируем, как работает это свойство логарифмов:

Правило работает и в обратную сторону:

Задание. Чему равна дробь

Третье правило помогает вычислять логарифм от частного или дроби.

Для доказательства этого свойства логарифмов воспользуемся уже доказанными нами двумя правилами. Но предварительно напомним, что произвольное число с в степени (– 1) представляет собой дробь 1/с:

Тогда доказательство будет записываться в две строчки:

С помощью полученной формулы возможно выполнить следующие преобразования:

Заметим, что все полученные формулы справедливы только в том случае, когда под знаком логарифма стоят исключительно положительные числа. Например, вполне допустимо преобразование

но ошибочной будет такая запись:

ведь в левой части стоит выражение, имеющее смысл, а в правой – выражение, смысла не имеющее.

Но что делать в случае, если необходимо упростить выражение с переменными, которые могут принимать как положительные, так и отрицательные значения? Получается, что запись

не является корректной. Действительно, если и х, и у являются отрицательными числами, то их произведение ху положительно. Но тогда получается, что при некоторых значениях переменных левая часть равенства имеет смысл, а правая – нет. Это значит, что оно не является тождеством.

Здесь может помочь использование модуля числа. Запись

уже будет корректной при любых допустимых значениях х и у. Если же хоть одна из переменных будет равна нулю, то обе части равенства одновременно потеряют смысл. Таким образом, данное равенство можно считать тождеством.

Аналогично и формулу разности логарифмов можно представить в более общем случае, при котором допускаются отрицательные значения переменных:

Можно ли записать равенство log_aх 2 = 2log_aх, если допускается, что х может быть и отрицательным? Нет, нельзя, ведь при отрицательных х выражение левая часть равенства будет иметь смысл, а правая нет. Однако использование модуля поможет и в этом случае. Можно написать, что

Аналогичным образом можно упростить и любые другие логарифмы, аргументы которых возведены в четную степень:

Ещё раз уточним, что эти правила используются при упрощении выражений с переменными, если те могут принимать отрицательные значения. Если же известно, что числа b и c положительны, то лучше использовать формулы, не содержащие модулей.

Переход к новому основанию алгоритма

До этого мы рассматривали преобразования, в ходе которых не менялось основание логарифма. Однако иногда возникает необходимость сложить или вычесть логарифмы с различными основаниями. Пусть надо вычислить значение выражения

Так как основания двух логарифмов различны, то мы не можем использовать выведенную нами формулу разности логарифмов. Однако можно попытаться привести один из логарифмов к новому основанию. Для такой операции существует специальная формула.

Докажем это утверждение. Для этого введем новые переменные:

Тогда по определению логарифма можно записать равенства

Отсюда следует, что a x = c y . Подставим в это равенство вместо а выражение c z и получим:

Отсюда следует, что zx = у, или х = y/z. Теперь заменим х, у и z на логарифмы и получим то самое тождество, которые необходимо доказать:

Вернемся к примеру

Теперь мы можем произвести эти вычисления, но для этого сначала приведем log₂₅9 к основанию 5:

Теперь можно вычислить, чему равна искомая разность:

Формула перехода к новому основанию позволяет иначе взглянуть на графики логарифмических функций. Пусть дана функция у =log₄x. Попытаемся привести ее к показателю 2:

Выходит, что график у = log₄x можно получить из графика у = log₂x его сжатием в 2 раза. Убедимся в этом, построив оба графика в одной плоскости:

Заметим, что и более общем случае графики функций у = log_ax и у = log_bx могут быть получены друг из друга растяжением или сжатием в некоторое число раз. Действительно, формулу перехода к новому основанию можно переписать в таком виде:

Теперь подставим вместо числа b переменную х и получим соотношение, связывающее любые две логарифмические функции:

В данном случае log_сx и log_ax – это логарифмические функции, а log_ca – некоторое число. В результате можно заключить, что график функции у = log_сx может быть получен из графика log_ax его растяжением в log_ca раз.

Попытаемся привести логарифм log_ab к обратному основанию, то есть к основанию 1/а:

Итак, log_ab = – log_1/аb. Именно из-за этого графики логарифмов с обратными основаниями (например, 2 и 0,5) симметричны относительно оси Ох:

Покажем примеры использования этой формулы:

А что будет, если мы попробуем log_ab привести к основанию b? Сделаем это:

Получили ещё одну замечательную логарифмическую формулу.

Её работу иллюстрируют следующие примеры:

Ещё одна логарифмическая формула позволяет возводить основание логарифма и его аргумент в одинаковую степень:

Докажем это тождество в «обратном порядке», то есть из правой части выведем левую. Для этого просто перейдем к основанию а:

Проиллюстрируем, как это свойство можно применять на практике:

Использование логарифма для вычислений

Исторически развитие теории логарифмов было связано с необходимостью выполнять громоздкие вычисления. Например, пусть надо возвести число 7 в пятисотую степень, то есть вычислить величину 7 500 . Сделать напрямую это довольно затруднительно. Однако в силу основного логарифмического тождества мы можем записать, что

Напомним, что десятичный логарифм обозначают символом lg, поэтому перепишем это равенство в более привычном виде:

Степень из-под знака логарифма можно вынести:

Значение числа lg 7 можно узнать с помощью калькулятора, в древности же использовали специальные таблицы, в которых были указаны десятичные логарифмы всех чисел от 1 до 10 (с маленьким шагом, равным, например, 0,001). Так или иначе, можно узнать, что

Получили число, записанное в стандартном виде. При этом наши расчеты были относительно простыми, если сравнить их с необходимостью умножить число 7 само на себя 500 раз. Аналогично и многие другие сложные операции выполняются значительно быстрее, если используются логарифмы. Поэтому долгое время знание теории логарифмов было необходимо для выполнения сложных инженерных расчетов. Но сегодня развитие компьютерной техники позволило избавиться от необходимости использования логарифмических линеек и таблиц.

Логарифмическая функция в природе и науке

Логарифм – это не просто инструмент для выполнения сложных операций. Например, в теории вероятностей существуют логарифмическое и логнормальное (от слов «логарифм» и «нормальное») распределение случайных величин, которые используются в генетике и физике. Так, размеры астероидов в Солнечной системе описываются логарифмическим распределением, а размеры градин во время града – логнормальным.

В компьютерной технике многие величин можно вычислить с использованием логарифмов. Например, ясно, что чем больше телефонных номеров находится в базе данных, тем дольше компьютер будет искать требуемый необходимый номер в ней. Зависимость времени поиска от количества номеров в базе данных описывается логарифмической функцией.

Огромное значение логарифмы имеют в астрономии. Так, яркость звезд на небе характеризуется таким параметром, как «видимая звездная величина». Однако в физике для оценки яркости света используют величину «освещенность», измеряемую в люксах. Зависимость между освещенностью звезд и их видимой величиной также является логарифмической.

Используются логарифмы и в термодинамике для вычисления такой характеристики систем, как энтропия. При расчете количества топлива, необходимого ракете для набора определенной скорости, используется формула Циолковского, содержащая натуральный логарифм:

В биологии давно замечено, что зависимость человеческих ощущений от силы воздействующих на них факторов окружающей среды носит логарифмический характер. В связи с этим для измерения громкости звуков используется специальная шкала децибелов, которая является логарифмической.

В строении ряда организмов можно обнаружить логарифмические кривые. Классическим примером является форма некоторых ракушек.