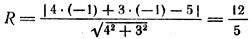Окружность каноническое и общее уравнение окружности

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

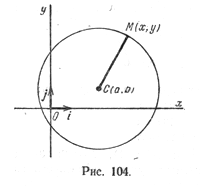
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = \( \sqrt <(x — a)^2 + (у — b)^2>\), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

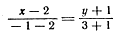
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

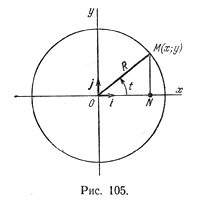
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

Уравнение окружности по заданному центру и радиусу в различных формах

Этот онлайн-калькулятор показывает уравнение окружности в стандартной, параметрической и общей формах, по заданному центру и радиусу окружности. Описание и формулы приведены под калькулятором

Уравнение окружности по заданному центру и радиусу в различных формах

Центр окружности

Уравнение окружности

Уравнение окружности — это алгебраический способ описания всех точек, лежащих на некоторой окружности. То есть если координаты точки x и y обращают уравнение окружности в равенство — эта точка принадлежит данной окружности. Существуют разные формы записи уравнения окружности:

• общее уравнение окружности
• стандартное уравнение окружности 1
• параметрическое уравнение окружности
• уравнение окружности в полярных координатах

Общее уравнение окружности

Общее уравнение окружности с центром и радиусом выглядит так:
,
где

В таком виде довольно сложно судить о свойствах заданной этим уравнением окружности, а именно, о координатах центра и радиусе. Но эту форму достаточно легко привести к стандартной форме (ниже), которая гораздо нагляднее.

Стандартное уравнение окружности

Стандартное уравнение окружности с центром и радиусом выглядит так:

Переход от общей формы к стандартной заключается в применении метода выделения полного квадрата. Получив стандартную форму, можно легко узнать координаты центра и радиус. Подробнее можно посмотреть здесь — Метод выделения полного квадрата и здесь — Нахождение центра и радиуса окружности по общему уравнению окружности.

Параметрическое уравнение окружности

Параметрическое уравнение окружности с центром и радиусом выглядит так:

Уравнение называется «параметрическим», потому что и x и y зависят от «параметра» тета. Это переменная, которая может принимать любые значения (но конечно это должно быть одно и то же значение в обоих уравнениях). Для параметрического уравнения используется определение синуса и косинуса в прямоугольном треугольнике построенном на радиусе и перпендикуляров от точки на окружности до координатных осей.

Уравнение окружности в полярных координатах

Для записи уравнения окружности в полярных координатах требуются полярные координаты центра окружности по отношению к началу координат. Если полярные координаты центра окружности — это , то полярные координаты точки окружности должны удовлетворять следующему уравнению:
,
где a — радиус окружности.

Так, во всяком случае, его называют в англоязычной литературе. Насчет русского термина я не уверен, по-моему эту форму рассматривают просто как еще один способ записи общего уравнения окружности, тем более что переход от общего уравнения к стандартному довольно простой. ↩

Окружность и ее уравнения

Окружностью называется геометрическое место точек плоскости, равноудаленных от одной точки, называемой центром окружности.

Построим уравнение окружности. Для этого, согласно определению, зададимся центром окружности и R – радиусом окружности L (рис.1). Возьмем произвольную точку M(x, y), которая по определению должна принадлежать окружности, следовательно, согласно определению, удовлетворять соотношению

. (2)

Запишем это выражение в координатах

.

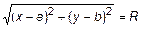
Окончательно получим уравнение окружности в каноническом виде

. (3)

2.1. Исследование окружности

1. Если , то выражение (3) примет вид .

2. Если , то выражение (3) примет вид .

3. Если , то выражение (3) примет вид .

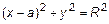
Приведем уравнение (3) к общему виду (1). Для этого раскроем скобки и умножим обе части равенства на число .

.

Введем обозначения: ; ; . Подставим эти обозначения и получим уравнение окружности в общем виде

. (4)

Признаки окружности:

— коэффициенты при квадратах текущих координат равны;

— отсутствует член, содержащий произведение текущих координат « ».

2.2. Последовательность перехода от общего

к каноническому виду

Для этого разделим все члены уравнения на коэффициент при и выделим полные квадраты с x и y.

Задано уравнение второго порядка: .

Построить кривую согласно.

Поскольку коэффициенты при квадратах одинаковы (=4) и отсутствует член , то можно сказать, что это окружность.

Это окружность (рис. 2) с радиусом R=4 и центром в точке C(1, -1.5).

Эллипс

Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых от двух данных точек, называемых фокусами, есть величина постоянная.

Зададим в декартовой системе координат фокусы F₁и F₂(рис. 3). Возьмем произвольную точку M(x, y), которая по определению должна принадлежать эллипсу. Проведем отрезки F₁M и F₂M (рис. 3). Согласно определению рассмотрим сумму этих отрезков

, (5)

где – некоторое число.

Обозначим , тогда из или . Фокусы имеют координаты и , причем – эллипс. Представим выражение (1) в координатах:

.

Перенесем второе слагаемое в правую часть и возведем обе части равенства в квадрат:

.

Раскроем скобки и сократим одинаковые члены равенства в левой и правой частях:

.

Возведем обе части равенства в квадрат:

.

Раскроем скобки и сократим одинаковые члены равенства в левой и правой частях:

,

.

Перенесем слагаемые с x и y в правую часть, остальные – в левую. Вынесем за скобки x 2 и a 2 :

. (6)

Отметим, что . Обозначим . Запишем выражение (6) через введенные обозначения

, . (7)

Выражение (7) есть уравнение эллипса в каноническом виде.

4. Исследование формы и расположения эллипса

по его каноническому виду

Рассмотрим выражение (7) и заметим следующее.

1. Так как текущие координаты входят в уравнение только в квадратах, то эллипс симметричен относительно осей координат – осей симметрии.

Если , то и .

Начало координат – центр симметрии. Плоскость, в которой лежат фокусы эллипса, называется фокальной плоскостью.

2. Эллипс L (7) пересекается с осями координат.

a) Пересечение с осью .

, . Из выражения (7) => . То есть точки и . Эти точки – вершины эллипса. – большая ось эллипса. Отметим эти точки на оси (рис. 4).

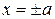
б) Пересечение с осью .

, . Из выражения (7) => . То есть, точки и . Две точки и – также вершины эллипса. – малая ось эллипса. Отметим эти точки на оси (рис. 4).

3. Из уравнения (7) найдем y

. (8)

Для I четверти выражение (8) имеет вид . При увеличении x от 0 до a (при x=a y=0) значение y уменьшается от b до 0. Поскольку эллипс симметричен относительно начала координат, то аналогичным образом, сохраняя симметрию, эллипс будет вести себя в остальных четвертях плоскости.

1. В частности, при из (7) имеем , (окружность – частный случай эллипса).

2. Если центр эллипса лежит не в начале координат, а в точке , то уравнение эллипса примет вид

. (9)

Эксцентриситетом называется величина, равная отношению расстояния между фокусами к длине большой оси.

, . (10)

Чем ближе эксцентриситет к 0 ( ), тем более округлую форму эллипс имеет, и наоборот, чем ближе эксцентриситет к 1 ( ), тем эллипс более вытянут вдоль оси .

Последовательность перехода от общего к каноническому виду для эллипса аналогична последовательности перехода для окружности. Для этого вынесем за скобки коэффициент при и выделим полный квадрат с x . Также вынесем за скобки коэффициент при и выделим полный квадрат с y.

В лекции изучены понятия «окружность» и «эллипс» в общем виде, показано, как строить графики этих функций. По общему виду уравнения второго порядка можно судить о виде кривой. Отметим:

— параметры R, a и b в выражении (3) определяют соответственно радиус и координаты центра окружности;

— от уравнения общего вида к каноническому переходят путем выделения полных квадратов;

— эксцентриситет эллипса ;

— эксцентриситет эллипса определяет его вытянутость;

— окружность – частный случай эллипса;

— фокусы эллипса могут быть найдены из выражения .

1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.

2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.

3. Шипачев В.С. Основы высшей математики. — М.: Высшая школа,1998.