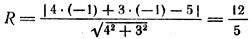Окружность задача уравнение x 1 y 2

Окружность задача уравнение x 1 y 2

Ответ:

Пошаговое объяснение:

a) центр т . (- 1 ; 2 ) ; радіус кола r = √16 = 4 .

А(- 1 ; 6 ) : (- 1 + 1 )² + ( 6 — 2 )² = 16 — правильна рівність ;

В( 3; 2) : ( 3 + 1 )² + ( 2 — 2 )² = 16 — правильна рівність ;

C(4; 0) : ( 4 + 1 )² + ( 0 — 2 )² = 16 — неправильна рівність .

Точки А і В належать даному колу .

2 . A(-1; 6) , В(3; 2) ; скористаємося формулою :

( x — x₁ )/( x₂ — x₁ ) = ( y — y₁ )/( y₂ — y₁ ) ;

( x + 1 )/( 3 + 1 ) = ( y — 6 )/( 2 — 6 ) ;

( x + 1 )/4 = ( y — 6 )/(- 4 ) ;

y = 6 — x — 1 = — x + 5 ; y = — x + 5 ; — рівняння прямої АВ .

Окружность задача уравнение x 1 y 2

Найти точки пересечения окружности ( x — 1) 2 + (y — 2) 2 = 4 и прямой y = 2x.

Координаты точек пересечения должны удовлетворять обоим указанным уравнениям, так как эти точки находятся как на одной, так и на другой линии. Решим систему уравнений

Подставляя в первое уравнение 2x вместо y и раскрывая скобки, получим

Подставляя эти значения во второе уравнение y = 2x, получим

и .

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

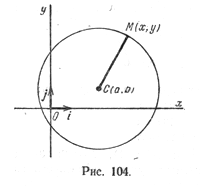
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = \( \sqrt <(x — a)^2 + (у — b)^2>\), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

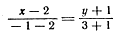
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

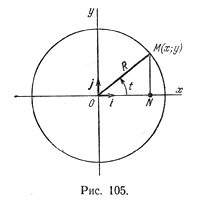
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем