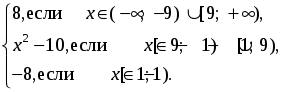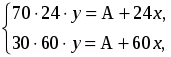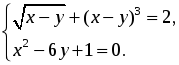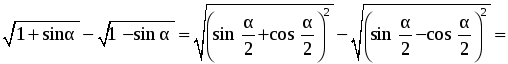Олимпиадные задания по математике для 11, 10 , 9 классов
олимпиадные задания по математике (9, 10, 11 класс)
Олимпиадные задания по математике для 11, 10, 9 классов (с решением заданий )
Скачать:
| Вложение | Размер |
|---|---|
| Олимпиадные задания по математике 11 класс | 36 КБ |
| олимпиадные задания по математике 10 класс | 58 КБ |
| olimpiadnye_zadaniya_po_matematike_9_klass.doc | 36 КБ |
Предварительный просмотр:
Олимпиадные задания по математике 11 класс (с решением)
Докажите, что произведение четырех последовательных целых чисел, сложенное с единицей, есть точный квадрат.
Решите уравнение sin 4 4x + cos 2 x = 2sin4x х cos 4 x.
Существует ли многогранник с нечетным числом граней,
каждая из которых есть многоугольник с нечетным числом сторон?
Докажите, что касательные к гиперболе y = 1/x образуют с осями координат треугольники одной и той же площади.
В каждую клетку квадратной таблицы 25 x 25 вписано произвольным образом одно из чисел 1 или -1.
Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце.
Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке.
Докажите, что сумма 50 написанных произведений не может оказаться равной нулю.
Пусть это 4 последовательных числа: n, n + 1, n + 2, n + 3.
Тогда n (n + 1)(n + 2)(n + 3) + 1 = ( 2 + 3n)(n 2 + 3n + 2) + 1 = (n 2 + 3n) 2 + 2(n 2 + 3n) + 1 = (n 2 + 3n + 1) 2 .
Перенесем в левую часть 2sin4x · cos 4 x и прибавим и вычтем по cos 8 x.
В результате полученное уравнение можно преобразовать к виду (sin4x – cos 4 x) 2 + cos 2 x(1 – cos 6 x) = 0,
которое равносильно следующей системе:
Решая второе уравнение и подставляя его решения в первое уравнение,
в результате получим решение исходного уравнения x = π /2 + π k .
Пусть такой многогранник существует. Обозначим за 1, 2, …, число ребер на гранях,
тогда 1 + 2 + … – удвоенная сумма всех ребер многогранника, она – четная.
А в левой части стоит нечетная сумма слагаемых, каждое из которых – нечетно.
Получили противоречие. Значит, такого многогранника не существует.
Составим уравнение касательных к гиперболе в точке
Т. к.(1/x)’ = -1/(x 2 ), то эти уравнения будут иметь вид y = -1/(х 0 2 )(x — х 0 ) + 1/х 0 . (*)
Касательная с уравнением (*) пересекает ось абсцисс в точке (х 1 ;0);
х 1 можно определить из уравнения -1/(х 0 2 )(x — х 0 ) + 1/х 0 = 0.
Решая данное уравнение, получим х 1 = 2х 0 .
Точка (0; y 1 ) пересечения с осью ординат определяется подстановкой в уравнение (*) значения х = 0.
В итоге получим y 2 = 2/х 0 .
Отрезки осей координат и касательной составляют прямоугольный треугольник,
катеты которого имеют длины а = 2|х 0 | и b = 2 / |х 0 |.
Площадь данного треугольника равна 2.
Найдем произведение всех 25 чисел,
записанных под каждым столбцом и всех 25 чисел, записанных справа от строчек.
Так как в этом произведении каждое из чисел квадратной таблицы входит по два раза, то произведение этих 50 произведений, в каждом из которых стоит по 25 множителей, будет положительным, т. е. равно 1.
А так как произведение 50 чисел положительно, то отрицательных сомножителей будет четное число (2, 4, …, 50).
Сумма же 50 произведений может быть нулем лишь в случае, когда 25 слагаемых равно 1, а 25 слагаемых равно — 1, т. е. слагаемых с — 1 должно быть нечетное число.
А это значит, что сумма 50 написанных произведений не может равняться нулю.
Олимпиадные задания по математике 10 класс с решением
10 вариантов олимпиадных заданий по математике для 10 класса с решением.
Просмотр содержимого документа
«Олимпиадные задания по математике 10 класс с решением»
1. Квадрат каждого из трех данных чисел равен произведению двух оставшихся чисел. Докажите, что все данные числа равны.
2. В каком году XX века родился человек, если в 1997 году произведение цифр лет, прожитых им, уменьшенное в 4 раза, на 3 меньше суммы цифр года его рождения?
3. Построить график функции y = | x 2 – 1 | – | x 2 – 9 |.
4. Периметр треугольника равен 24 см. Можно ли около этого треугольника описать окружности радиусом 5 см?
5. Докажите, что при любом значении x выполняется равенство:
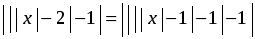
6. Трава на лугу растет одинаково густо и быстро. Известно, что 70 коров съели бы ее за 24 дня, а 30 коров – за 60 дней. Сколько коров съели бы всю траву за 96 дней?
По условию имеем a 2 = bc; b 2 = ac; c 2 = ab. умножим эти равенства на a, b, c соответственно получим, что a 3 = b 3 = c 3 = abc, но если равны кубы чисел, то равны и сами эти числа.
2. 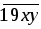
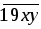
1997 – (100 + 9 ∙ 100 + 10x + y) = 10 ∙ (9 – x) + (7 – y) – возраст 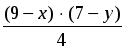
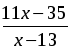
Единственное решение в целых числах: x = 1; y = 2.
Необходимо рассмотреть 2-й случай, когда y 7, тогда
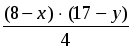
x = 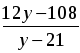
Ответ: 1912 год, 1909 год.
3. y = | x 2 – 1 | – | x 2 – 9 | преобразовать к виду кусочно-заданной функции и построить график
y = f (x) =
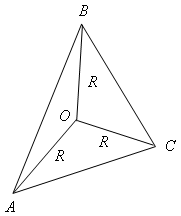
4. Пусть ∆ABC – некоторый треугольник и О – центр описанной около него окружности с радиусом R.
5. Можно построить графики обеих частей уравнения, используя преобразование графиков функций, возможно аналитическое решение уравнения, но тогда потребуется рассмотрение 6 случаев возможного значения переменной x.
Пусть было на лугу A кг травы и растет она со скоростью x кг в день. Одна корова съедает y кг травы в день, получаем следующую систему:
а необходимо найти такое число z, что 96 ∙ z ∙ y = A + 96x. Используя систему уравнений, получим, что z = 20.
1. Упростить выражение 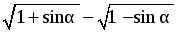
2. Вычислить a 4 + b 4 + c 4 , зная, что a + b + c = 0 и a 2 + b 2 + c 2 = 1.
3. Найти сумму целых решений неравенства: 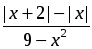
4. Точки P, K, M, N – соответственно середины сторон AB, BC, CD, DA выпуклого четырехугольника ABCD. Отрезки AK и CP пересекаются в точке F, отрезки AM и CN – в точке E. Площадь четырехугольника AFCE равна 666. Найдите площадь четырехугольника ABCD.
5. Найдите площадь фигуры, заданной неравенством:
6. Решить систему уравнений:
1.
= 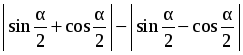
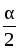
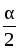
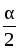
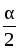
= 2sin 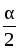
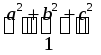
ab + bc + ac = 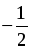
(ab + bc + ac) 2 = 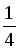
a 2 b 2 + b 2 c 2 + a 2 c 2 + 2acb 2 + 2a 2 bc + 2bac 2 = 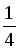
a 2 b 2 + b 2 c 2 + a 2 c 2 + 2abc (a + b + c) = 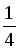
a 2 b 2 + b 2 c 2 + a 2 c 2 = 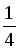
2a 2 b 2 + 2b 2 c 2 + 2a 2 c 2 = , имеем, что
5. Фигура представляет собой квадрат с центром в точке (5; –9) и диагональю, равной 8, поэтому площадь равна = 32.
6. Обозначим = t, причем t ≥ 0;
t + t 6 = 2; t 6 + t – 2 = 0; t = 1 – корень данного уравнения.
то есть y 2 – 6y + 1 = 0.
Ответ: (3 + 2 ; 3 + 2 ); (3 – 2 ; 3 – 2 ).
1. Вычислить , если tg = 2.
2. Решите систему уравнений
3. Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором
AB = AA1 = 12, AD = 30. Точка М расположена на грани ABB1A1 на расстоянии 1 см от середины AB и на равных расстояниях от A и B. Точка N принадлежит грани DCC1D1 и расположена симметрично точке М относительно центра параллелепипеда. Найти длину кратчайшего пути по поверхности параллелепипеда между точками М и N.
4. Из точки Е к окружности диаметром KМ проведена касательная ЕМ. Отрезок ЕK пересекается с окружностью в точке D, ED = 2 дм; KМ = 6 дм. Найдите градусную меру дуги окружности, заключенной внутри ∆MEK.
5. Найдите сумму 1 + 11 + 111 + 1111 + . + 11. 1 (всего 2000 слагаемых).
6. Решить графически систему уравнений:
Решим первое уравнение системы относительно x.
= (y + 19) 2 – 50y 2 + 60y – 410 = –49y 2 + 98y – 49 =
= –49 (y 2 – 2y + 1) = –49 (y – 1) 2 .
Очевидно, что уравнение имеет решение лишь при y = 1; найдем x:
10x 2 – 40x + 40 = 0; x 2 – 4x + 4 = 0; (x – 2) 2 = 0; x = 2.
Проверкой убеждаемся, что пара x = 2; y = 1 является решением второго уравнения системы.
4. Найти градусную меру дуги MD.
MDK = 90°, так как опирается на диаметр.
tg MKD = , то есть MKD = 30°, а значит, MD = 60°.
5. 9 ∙ (1 + 11 + . + 1. 1) = 9S;
(10 – 1) + (100 – 1) + . = 9S;
9S = 10 + 10 2 + 10 3 + . + 10 2000 – 2000;
1. Найти сумму натуральных чисел от 1 до 1000, которые делятся на 7 и не делятся на 13.
2. Решить систему уравнений:
3. Постройте график функции:
4. Дан выпуклый пятиугольник, все углы которого тупые. Доказать, что в нем найдутся две такие диагонали, что круги, построенные на них, как на диаметрах, полностью накроют пятиугольник.
5. Сколько одинаковых членов находится в двух арифметических прогрессиях 5; 8; 11. и 3; 7; 11. если в каждой из них по 100 членов?
6. По дороге мимо наблюдателя проехали через равные промежутки времени автобус, мотоцикл и автомобиль. Мимо другого наблюдателя они проехали с такими же промежутками времени, но в другом порядке: автобус, автомобиль и мотоцикл. Найти скорость автобуса, если скорость автомобиля 60 км/ч, а скорость мотоцикла 30 км/ч.
2. Из первого уравнения следует | x | ≤ 1; | y | ≤ 1; | z | ≤ 1.
Если | x | y | z | x 3 + y 3 + z 3 x 2 + y 2 + z 2 = 1, но это неверно. Поэтому, если | x | = 1, то | y | = 0, | z | = 0. а из второго уравнения следует, что x = 1. Аналогично рассуждаем для | y | = 1 или | z | = 1.
Ответ: (1; 0; 0); (0; 1; 0); (0; 0; 1).
3. Графиком является прямая y = 3.
4. На диагоналях АС и AD построим круги, как на диаметрах с центрами O1 и O2. Они накроют ∆ABC и ∆AED, так как углы B и Е тупые. Если один из углов ACD и ADE тупой, то один из кругов с центром O1 и O2 покрывает ∆ACD. Если углы ACD и ADC не тупые, то круг с центром O1 покрывает ∆AHC, а круг с центром O2 покрывает ∆ADH. Значит, круги с центрами O1 и O2 полностью покрывают пятиугольник.
5. Пусть некоторые члены арифметических прогрессий равны:
5 + (n – 1) ∙ 3 = 3 + (m – 1) ∙ 4;
≤ k ≤ 25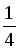
Ответ: общих членов 25 штук.
6. Пусть S – расстояние между наблюдателями, x – скорость автобуса, t – промежуток времени, через которое мимо первого наблюдателя последовательно проехали автобус, мотоцикл, автомобиль. Тогда время, затраченное автобусом, мотоциклом и автомобилем на пути от одного наблюдателя до другого, равно ; и соответственно, а из условия задачи имеем = + t; = – t.
Сложив их, получим , откуда x = 40. Значит, скорость автобуса равна 40 км/ч.
1. Остаток при делении многочлена P (x) на (x – 1) равен 1, при делении P (x) на (x – 2) равен 2, а при делении P (x) на (x – 3) равен 3. Какой остаток будет при делении P (x) на (x – 1)(x – 2)(x – 3)?
3. Войсковая колонна имеет длину 5 км. Связной, выехав из конца колонны, передал пакет в начало колонны и вернулся обратно. Колонна за это время прошла путь в 12 км. Какой путь проехал связной?
4. Решите в целых числах систему уравнений:
5. Найти площадь фигуры, заданной на координатной плоскости неравенством x 2 + y 2 ≤ 10 | x | + 4 | y |.
6. Найдите радиус окружности, описанной около правильного девятиугольника ABCDEFGHK, если известно, что площадь ∆ADG равна 48 .
oткуда a = 1; b = –2; c = 1, то есть остаток x 2 – 2x + 1.
2. Прежде всего надо отметить, что y ≥ 0.
При y = 0 x – любое, кроме x = + πk; k Z, то есть график представляет собой совокупность прямых x = πk; k Z, параллельных оси ОY и оси ОХ с выколотыми точками x = + πk; k Z.
3. S = 5 км; x – скорость колонны, y – скорость связного.
Откуда ∙ y = = 18 (км) проехал связной.
5. Достаточно рассмотреть случай для x ≥ 0; y ≥ 0, так как выражение симметрично относительно x, y:
x 2 – 10x + 25 + y 2 – 4y + 4 – 29 ≤ 0;
(x – 5) 2 + (y – 2) 2 ≤ 29 – окружность с центром в точке (5; 2) и радиусом . Sфигуры = 58π + 80.
AO = R – окружности, описанной около ∆ADG;
1. Вычислить, не пользуясь таблицами и микрокалькулятором,
tg 1° ∙ tg 2° ∙ tg 3° ∙ . ∙ tg 89°.
2. Решить уравнение: = 3x.
3. Найдите два трехзначных числа, сумма которых кратна 504, а частное кратно 6.
4. Непрерывная четная функция y = f (x) определена на всей числовой прямой. Для всех неотрицательных значений x значение f (x) совпадает со значением функции g (x) = x 2 – 6x + 5. Найдите произведение корней уравнения f (x) = –3.
5. 30 стульев стоят в ряд. Время от времени к ряду подходит человек и садится на один из свободных стульев, при этом один из его соседей, если таковые есть, встает и уходит. Какое максимальное число стульев может быть занято, если в начале они все были пустыми?
6. Найти наименьшее значение параметра с, при котором система имеет одно решение.
1. tg 1° ∙ tg 2° ∙ tg 3° ∙ . ∙ tg 87° ∙ tg 88° ∙ tg 89° =
= tg 1° ∙ tg 2° ∙ . ∙ tg (90 – 2)° ∙ tg (90 – 1)° =
= tg 1° ∙ tg 2° ∙ . ∙ ctg 2° ∙ ctg 1° = 1.
Использовать тождество tg ∙ ctg = 1.
2. Умножим обе части уравнения на сопряженное выражение:
6x = 3x ∙ (), откуда с учетом того,
что x ≥ 0, получаем корни уравнения x1 = 0; x2 = 4.
3. Пусть a и b – искомые трехзначные числа, тогда
где f и k – целые числа, но так как числа a и b – трехзначные, то k = 1 – единственное значение, удовлетворяющее условию задачи.
Возможные значения f: 2, 3, 4, 5… 13 при f = 2; b = 144; a = 864, дальнейшие значения f рассматривать не имеет смысла.
Возможен графический способ решения.
1. Найдите значение выражения , если
2. Постройте график функции y = 4 sin x ∙ | cos x |.
3. Сумма третьего и четырнадцатого членов арифметической прогрессии равна наибольшему значению трехчлена –2x 2 + 4x – 16. Найдите сумму шестнадцати первых членов этой прогрессии.
4. Составьте формулу, с помощью которой выражался бы n-й член последовательности вида 0; 2; 2; 4; 4; 6; 6; .
5. В сосуде имеется три крана. Через первый и второй краны вода вливается, через третий выливается. Один первый кран может наполнить сосуд за 10 часов, а один второй – за 15 часов. При совместном действии всех трех кранов из полного сосуда выливается вся вода за 30 часов. Сосуд был полон, когда открыли первый и третий краны. Через 1 час после их открытия первый кран был закрыт, но открыт второй, а еще через 1 час закрыли третий кран и вновь открыли первый.
Определите, через сколько часов после закрытия третьего крана два первых наполнят сосуд.
6. Разность катетов прямоугольного треугольника равна биссектрисе прямого угла. Вычислите отношение этих катетов.
6. Пусть катеты прямоугольного ∆ABC равны a и b. Через вершину В проведем прямую, параллельную биссектрисе СЕ и пересекающую продолжение катета АС в точке D.
∆ABD и ∆ACE подобны, значит, , или CE = , но по условию = b – a (b a), отсюда находим b 2 – ab – a 2 = 0; , но 0, поэтому .
1. Найти в градусах угол , под которым окружность x 2 + y 2 = 32 видна из точки А (8; 0).
2. Сто человек ответили на вопрос: «Будет ли новый президент лучше прежнего?» Из них a человек считают, что будет лучше, b – что будет такой же и c – что будет хуже. Других ответов не было. Социологи построили два показателя «оптимизма» опрошенных: m = a + ; n = a – c. Оказалось, что m = 40. Чему в таком случае равно n?
3. Через точку М на диаметре окружности проводится секущая CD под углом 45° к диаметру. Докажите, что число | CM | 2 + | DM | 2 не зависит от положения точки М на диаметре.
4. Решить неравенство: ≥ 0.
5. Решить уравнение: 3 ∙ cos x – cos 3x = 2 (x 2 + ) + π ∙ .
6. Возраст одного человека в 1990 году был равен произведению цифр года его рождения. В каком году он родился, если известно, что ему меньше 90 лет?
2. Учитывая, что c = 100 – a – b, получаем:
значит, n = 2 ∙ 40 – 100 = –20.
3. Для доказательства: постройте точку D′, симметричную точке D относительно диаметра.
5. Использовать метод оценки для функций
наибольшее значение функции f равно наименьшему значению функции g (x) в двух точках: x1 = ; x2 = . можно использовать графическую иллюстрацию решения.
1. Дан угол в 19°. Построить с помощью циркуля и линейки угол в 1°.
2. Найдите три числа, если куб первого числа на 2 больше их произведения. Куб второго числа на 3 меньше их произведения, а куб третьего числа на 3 больше их произведения.
3. Решить неравенство: .
4. Четырехугольник АВСD вписан в окружность. Продолжение стороны AB за точку B пересекается с продолжением стороны CD в точке E.
Найти угол ADE, если CD = 2EB; AB : EC = 7 : 2, косинус угла AED равен .
5. Доказать тождество: 2 (sin 6 x + cos 6 x) – 3 (sin 4 x + cos 4 x) + 1 = 0.
6. При каких значениях параметра а уравнение | x 2 – 5x + 4 | = ax имеет ровно три корня?
1. Необходимо воспользоваться тем, что 19° ∙ 19 = 361°.
2. Пусть x, y, z – данные числа, тогда
t 3 = (t + 2) ∙ (t – 3) ∙ (t + 3) 2t 2 – 9t – 18 = 0. t1 = 6; t2 = , значит, xyz = 6 или xyz = , откуда необходимо рассмотреть решение двух систем уравнений:
4. По свойству секущей и касательной имеем BE ∙ (AB + BE) =
= EC ∙ (DC + EC). Пусть BE = x, AB = 7y, DC = 2x, EC = 2y; подставляя в предыдущее равенство, получим, что x = y.
Из ∆BCE по теореме косинусов BC = ; ADE = CBE, поэтому из ∆BEC CBE = π – arccos ; ADE = CBE.
5. 2 (sin 2 x + cos 2 x) ∙ (sin 4 x – sin 2 x cos 2 x + cos 4 x) – 3 (sin 4 x + cos 4 x) + 1 =
= –sin 4 x – 2sin 2 x cos 2 x – cos 4 x + 1 = –(sin 2 x + cos 2 x) 2 + 1 = 0.
6. При a = 1 можно использовать графическую иллюстрацию аналитического решения.
1. Найти значение выражения x 3 – 3x при x = .
2. Найти все решения уравнения , удовлетворяющие условию ctg x
3. Вычислить arccos (cos 10).
4. Составить уравнение окружности наименьшего радиуса, внутри которой помещается множество точек, заданной на координатной плоскости условием: | 3x – y – 1 | + | 3x – 6 |
5. Хорда окружности удалена от центра на расстояние h. В каждый из сегментов, стягиваемых хордой, вписан квадрат так, что две соседние вершины квадрата лежат на дуге, две другие – на хорде. Чему равна разность сторон этих квадратов?
6. В компании из шести человек один правдолюб, то есть всегда говорит правду; двое – дипломаты, то есть могут говорить правду или ложь; а остальные – лжецы, то есть всегда лгут. Чтобы узнать, кто из них есть кто, каждого спросили, кто он есть. Первый сказал, что правдолюб, второй – что он дипломат, третий – что он лжец, четвертый – что он не правдолюб, пятый – что он не дипломат, а шестой – что он не лжец.
Кто из них есть кто?
1. Найти значение выражения x 3 – 3x при x = .
2. Найти все решения уравнения , удовлетворяющие условию ctg x
3. Вычислить arccos (cos 10).
4. Составить уравнение окружности наименьшего радиуса, внутри которой помещается множество точек, заданной на координатной плоскости условием: | 3x – y – 1 | + | 3x – 6 |
5. Хорда окружности удалена от центра на расстояние h. В каждый из сегментов, стягиваемых хордой, вписан квадрат так, что две соседние вершины квадрата лежат на дуге, две другие – на хорде. Чему равна разность сторон этих квадратов?
6. В компании из шести человек один правдолюб, то есть всегда говорит правду; двое – дипломаты, то есть могут говорить правду или ложь; а остальные – лжецы, то есть всегда лгут. Чтобы узнать, кто из них есть кто, каждого спросили, кто он есть. Первый сказал, что правдолюб, второй – что он дипломат, третий – что он лжец, четвертый – что он не правдолюб, пятый – что он не дипломат, а шестой – что он не лжец.
Кто из них есть кто?
(2 ∙ (3 + ) + 1 – 2 ) 2sin x = 7 –1 ;
sin x = 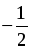
3. arccos (cos 10) = arccos (cos (4π – 10)) = 4π – 10, так как
(4π – 10) [0; π].
4. Рассмотрим четыре случая:
Множество точек, заданных полученными условиями, представляют собой параллелограмм ABCD, O – точка пересечения диагоналей. AC – большая диагональ, OC = R – радиус: (x – 2) 2 + (y – 5) 2 = (необходима графическая иллюстрация решения).
6. Первый, второй, шестой – лжецы; третий, четвертый – дипломаты; пятый – правдолюб.
Олимпиадные задания по математике для 10 класса с ответами
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Олимпиадные задания для учащихся 10 класса_2017_Соснина Л.А._простой вариант.docx
Олимпиадные задания для учащихся 10 класса
Решить в целых числах уравнение xy + 3 x – 5 y = – 3.
У нумизмата есть 100 одинаковых по внешнему виду монет. Он знает, что среди них 30 настоящих и 70 фальшивых монет. Кроме того, он знает, что массы всех настоящих монет одинаковы, а массы всех фальшивых – разные, причём каждая фальшивая монета тяжелее настоящей; однако точные массы монет неизвестны. Имеются двухчашечные весы без гирь, на которых можно за одно взвешивание сравнить массы двух групп, состоящих из одинакового числа монет.
За какое наименьшее количество взвешиваний на этих весах нумизмат сможет гарантированно найти хотя бы одну настоящую монету?
Наконец, у Снежной Королевы появились все квадраты с целыми сторонами, но каждый в единственном экземпляре. Королева пообещала Каю, что он станет мудрым, если сможет из каких-то имеющихся квадратов сложить прямоугольник. Сможет ли он это сделать?
В выпуклом четырехугольнике равны длины отрезков, соединяющих середины противоположных сторон, а длины диагоналей равны 4 и 5. Найдите площадь данного четырехугольника.
На квадратном поле из 121 клетки десять клеток поросли бурьяном. После этого бурьян может распространиться на клетку, у которой не менее двух соседних клеток уже поросли бурьяном. Какое наибольшее число клеток может порасти бурьяном?
Ответы к олимпиадным заданиям для учащихся 10 класса
Решить в целых числах уравнение xy + 3 x – 5 y = – 3.
xy + 3 x – 5 y-15 = – 3– 15
( xy – 5 y )+( 3 x-15 ) = – 18
y ( x -5)+3( x -5) = – 18
Запишем уравнение в виде ( x – 5)( y + 3) = – 18. Его решения соответствуют представлениям числа –18 в виде произведения двух целых чисел.
(–13, –2), (–4, –1), (–1, 0), (2, 3), (3, 6), (4, 15), (6, –21), (7, –12),
У нумизмата есть 100 одинаковых по внешнему виду монет. Он знает, что среди них 30 настоящих и 70 фальшивых монет. Кроме того, он знает, что массы всех настоящих монет одинаковы, а массы всех фальшивых – разные, причём каждая фальшивая монета тяжелее настоящей; однако точные массы монет неизвестны. Имеются двухчашечные весы без гирь, на которых можно за одно взвешивание сравнить массы двух групп, состоящих из одинакового числа монет.
За какое наименьшее количество взвешиваний на этих весах нумизмат сможет гарантированно найти хотя бы одну настоящую монету?
Сложим все 100 монет в кучу. Каждым взвешиванием нумизмат будет выбирать две монеты из кучи и сравнивать их. Если их массы равны, то обе монеты настоящие, и требуемая монета найдена. Если же нет, то более тяжёлая монета – фальшивая, и её можно выбросить из кучи.
Через 70 таких взвешиваний, если равенства никогда не будет, то в куче останется 30 монет, причём все настоящие останутся в куче. Значит, в этом случае нумизмат даже найдёт все 30 настоящих монет. Таким образом, 70 взвешиваний достаточно.
Оценка . Предположим, что у нумизмата есть алгоритм, позволяющий гарантированно найти настоящую монету не более, чем за 69 взвешиваний. Мы покажем, что это невозможно – даже в предположении, что массы монет таковы: масса настоящей равна 2 100 , а масса m i i -й фальшивой равна 2 100 + 2 i .
При таком предположении результат любого взвешивания можно определить так. Пусть при некотором взвешивании на чашках по k монет, среди которых d > 0 фальшивых, имеющих номера i 1 i 2 i d . Тогда на чашке, на которой лежит самая тяжёлая монета, суммарная масса не меньше k ·2 100 + 2 i d , а суммарная масса на другой чашке не больше k ·2 100 + (2 1 + . + 2 i d –1 ) = k ·2 100 + 2 i d – 2. Значит, если на чашках есть хотя бы одна фальшивая монета, то перевесит чашка, на которой лежит фальшивая с наибольшим номером.
Итак, пусть нумизмат действует по своему алгоритму. Мы будем сообщать ему результаты взвешиваний и присваивать некоторым монетам массы m i . При этом после каждого взвешивания присвоенными окажутся веса m 70 , m 69 , . m 70– i при некотором i . Если соответствующие монеты действительно имеют такие массы (а остальные массы распределены как угодно), то результаты взвешиваний будут такими, как мы сообщили.
При первом взвешивании выберем любую монету на чашках, присвоим ей массу m 70 и сообщим, что чашка с ней тяжелее. При каждом следующем взвешивании, если на весах уже присутствует монета с присвоенной массой, то мы выберем из таких масс наибольшую и сообщим, что чашка с соответствующей монетой перевесила. Если же никакой монете на весах масса ещё не присвоена, то мы опять выберем любую монету на чашках, присвоим ей наибольшую ещё не присвоенную массу и сообщим, что чашка с ней тяжелее. Нетрудно видеть, что при этом требуемые условия соблюдаются.
Если нумизмат совершил не более 69 взвешиваний, то не более 69 масс окажутся присвоенными. В частности, m 1 присвоенной не будет. Значит, массу m 1 может иметь любая монета, которой масса ещё не присвоена, и при этом все результаты взвешиваний останутся такими, как мы сообщили. Поэтому нумизмат не сможет указать на заведомо настоящую монету.
За 70 взвешиваний.
Наконец, у Снежной Королевы появились все квадраты с целыми сторонами, но каждый в единственном экземпляре. Королева пообещала Каю, что он станет мудрым, если сможет из каких-то имеющихся квадратов сложить прямоугольник. Сможет ли он это сделать? Если сможет сделать рисунок.
Можно составить прямоугольник 33×32 из 9 попарно различных квадратов так, как показано на рисунке.
Замечание . Из меньшего числа попарно различных квадратов составить прямоугольник нельзя, но можно это сделать из любого числа квадратов, большего 9. Для этого достаточно приставить квадрат к стороне имеющегося прямоугольника, составленного из n квадратов.
В выпуклом четырехугольнике равны длины отрезков, соединяющих середины противоположных сторон, а длины диагоналей равны 4 и 5. Найдите площадь данного четырехугольника.
Пусть ABCD — данный выпуклый четырехугольник, а K, L, M и N — середины его сторон AB, BC, CD и DA соответственно. Заметим, что отрезки KL и MN являются средними линиями в треугольниках ABC и ACD. Поэтому они оба равны половине диагонали AC и параллельны AC. Значит, четырехугольник KLMN является параллелограммом (1 признак параллелограмма). По условию его диагонали KM и LN равны. Следовательно, четырехугольник KLMN является прямоугольником. Поскольку его сторона KL параллельна диагонали AC и LM параллельна диагонали BD изначального четырехугольника, то диагонали AC и BD перпендикулярны. По формуле площади четырехугольника : S=1/2 ⋅ AC ⋅ BD. Таким образом, S=1/2 ⋅ AC ⋅ BD=10.
На квадратном поле из 121 клетки десять клеток поросли бурьяном. После этого бурьян может распространиться на клетку, у которой не менее двух соседних клеток уже поросли бурьяном. Какое наибольшее число клеток может порасти бурьяном?
Заметим, что периметр поросшей бурьяном территории не увеличивается. Если рядом с клеткой, которая на которой вырастает бурьян, было три или четыре поросших бурьяном клетки, то он уменьшается, а если только две, то остаётся неизменным. Изначально он не больше, чем 10 ⋅ 4=40. Наибольшая площадь при данном периметре достигается в случае квадрата со стороной 10. Примером изначальной рассады бурьяна служит поросшая бурьяном главная диагональ без угловой клетки.
Несложно убедиться, что площадь бурьяна является полуинвариантом (она не уменьшается).
http://multiurok.ru/files/olimpiadnyie-zadaniia-po-matiematikie-10-klass-s-r.html
http://infourok.ru/olimpiadnie-zadaniya-po-matematike-dlya-klassa-s-otvetami-2739569.html