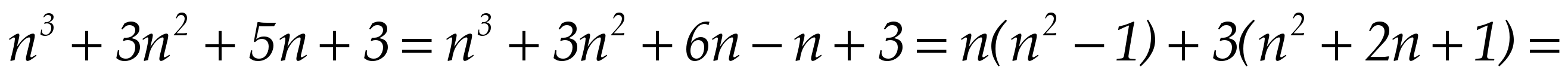Олимпиадные задания по математике 11 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Выберите документ из архива для просмотра:
Выбранный для просмотра документ М-11_кл.doc
Олимпиадные задания по математике
Общее время выполнения работы – 4 урока, 180 минут.
Общее максимальное количество баллов — 35 (по 7 баллов за каждое задание).
Докажите, что 13!-11! кратно 31.
Служившему воину дано вознаграждение за первую рану 1 копейка, за другую – 2 копейки, за третью – 4 копейки, за четвертую – 8 копеек и т.д. По исчислению нашлось, что воин получил всего вознаграждения 655 руб. 35 копеек. Спрашивается число его ран.
Решите уравнение
Три шара радиуса R касаются друг друга, а четвертый шар того же радиуса лежит сверху, при этом касается каждого из трех данных шаров. Определите высоту «горки» из четырех шаров.
Среди n рыцарей каждые двое – либо друзья, либо враги. У каждого из рыцарей ровно три врага, причём враги его друзей являются его врагами. При каких n такое возможно?
Критерии оценивания олимпиадных заданий
Общее максимальное количество баллов — 35 (по 7 баллов за каждое задание).
Докажите, что 13!-11! кратно 31.
Решение. Так как 13!=1 


















Критерии оценивания задания №1
Полное верное решение.
Решение верное. Имеются небольшие недочеты, в целом не влияющие на решение.
Приведены верные рассуждения, правильно записано разложение на множители 11!
Верно применена формула для нахождения факториалов 11! и 13!
Решение неверное, продвижения отсутствуют ИЛИ решение отсутствует
Служившему воину дано вознаграждение за первую рану 1 копейка, за другую – 2 копейки, за третью – 4 копейки, за четвертую – 8 копеек и т.д. По исчислению нашлось, что воин получил всего вознаграждения 655 руб. 35 копеек. Спрашивается число его ран.
Решение. 1 + 2 + 4 + 8 + … + 2 n = 65535 – это сумма геометрической прогрессии, где а 1 = 1, а 2 = 2, и т.д. Таким образом, q = 2. Формула суммы геометрической прогрессии

Критерии оценивания задания №2
Полное верное решение.
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
Ход решения задачи верный, правильно используется формула для подсчета суммы членов геометрической прогрессии, но допущена вычислительная ошибка. Решение может стать правильным после небольших исправлений.
Ход решения задачи верный, записана формула для подсчета суммы членов геометрической прогрессии, дальнейшие продвижения в решении задачи отсутствуют.
Правильно сделан вывод о том, что сумма вознаграждения равна сумме членов геометрической прогрессии.
Задание не решено (неверное решение) или записан ответ без объяснения.
Решите уравнение
Решение. Воспользуемся формулой для синуса двойного угла: 











Ответ: 

Примечание. Если в ответе учащийся записал две серии решения 


Критерии оценивания задания №3
Полное верное решение.
Ход решения верный, все шаги его выполнены. Имеются недочеты (даны неполные объяснения), в целом не влияющие на решение. ИЛИ полное верное решение, но не записан ответ.
Рассмотрены отдельные шаги решения. От уравнения 

Рассмотрены отдельные шаги решения. От уравнения 

Для первых 2-3 множителей правильно применили формулу для синуса двойного угла.
Задание не решено (неверное решение) или записан ответ без объяснения.
Три шара радиуса R касаются друг друга, а четвертый шар того же радиуса лежит сверху, при этом касается каждого из трех данных шаров. Определите высоту «горки» из четырех шаров.
Решение. Пусть четыре шара радиуса R c центрами A, B, C, D касаются друг друга и первые три из них – плоскости α в точках A 1 , B 1 , C 1 (см. рис).
Тогда точки A, B, C, D являются вершинами правильной пирамиды с ребром 2R.
Вершина D этой пирамиды проектируется в центр основания О.
А

Высота «горки» из четырех шаров равна сумме OD +2 R =2 R 
Ответ: 2 R ( 
Критерии оценивания задания №4
Полное верное решение.
Ход решения верный, все шаги его выполнены. Имеются недочеты (даны неполные объяснения), в целом не влияющие на решение. Решение может стать правильным после небольших исправлений или дополнений
Верно найдено расстояние OD .
Рассмотрены отдельные шаги решения. Верно найдено расстояние АО.
Правильно сделан вывод о том, что расстояние между центрами шаров равно 2R ИЛИ выполнен рисунок по условию задачи.
Задание не решено (неверное решение) или записан ответ без объяснения
Среди n рыцарей каждые двое – либо друзья, либо враги. У каждого из рыцарей ровно три врага, причём враги его друзей являются его врагами. При каких n такое возможно?
Решение. Из условия следует, что рыцарей – не менее четырёх. Заметим, что у рыцаря не может быть более двух друзей, иначе найдутся 4 рыцаря, у которых есть общий враг, но тогда у этого врага будет не менее четырёх врагов, что противоречит условию. Значит, у каждого рыцаря не более двух друзей и ровно три врага, следовательно, всего рыцарей – не более шести.
Так как у каждого рыцаря по 3 врага, то число рыцарей чётно .
б ) Примеры : если рыцарей – 4, то друзей ни у кого из них нет и каждый враг каждому, а если рыцарей – 6, то разбиваем рыцарей на две тройки: каждый рыцарь дружит с рыцарями из своей тройки и враждует с рыцарями из другой.
Ответ: n = 4 или n = 6.
Критерии оценивания задания №5
Полное верное решение.
Ход решения верный, все шаги его выполнены. Имеются недочеты (даны неполные объяснения), в целом не влияющие на решение. ИЛИ полное верное решение, но не записан ответ.
Верно выполнены рассуждения, но допущена логическая ошибка. Решение может стать правильным после небольших исправлений или дополнений.
Рассмотрены его отдельные шаги. Верно сделан вывод о том, что « у каждого рыцаря не более двух друзей и ровно три врага». Дальнейшие продвижения в решении задачи отсутствуют.
Решение начато верно. Рассмотрены его отдельные шаги, но дальнейшие продвижения в решении задачи отсутствуют. ИЛИ решение не доведено до конца.
Задание не решено (неверное решение) или записан ответ без объяснения.
Краткое описание документа:
Олимпиадные задания по математике 11 класс рассчитаны для проведения различных внеурочных мероприятий.
К заданиям приведены полные решения,критерии оценки каждого задания чётко разработаны.
При оценивании заданий могут быть рассмотрены другие способы решений задач.
При составлении заданий учитывались индивидуальные возможности учащихся.
Олимпиадные задания по математике для 11, 10 , 9 классов
олимпиадные задания по математике (9, 10, 11 класс)
Олимпиадные задания по математике для 11, 10, 9 классов (с решением заданий )
Скачать:
| Вложение | Размер |
|---|---|
| Олимпиадные задания по математике 11 класс | 36 КБ |
| олимпиадные задания по математике 10 класс | 58 КБ |
| olimpiadnye_zadaniya_po_matematike_9_klass.doc | 36 КБ |
Предварительный просмотр:
Олимпиадные задания по математике 11 класс (с решением)
Докажите, что произведение четырех последовательных целых чисел, сложенное с единицей, есть точный квадрат.
Решите уравнение sin 4 4x + cos 2 x = 2sin4x х cos 4 x.
Существует ли многогранник с нечетным числом граней,
каждая из которых есть многоугольник с нечетным числом сторон?
Докажите, что касательные к гиперболе y = 1/x образуют с осями координат треугольники одной и той же площади.
В каждую клетку квадратной таблицы 25 x 25 вписано произвольным образом одно из чисел 1 или -1.
Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце.
Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке.
Докажите, что сумма 50 написанных произведений не может оказаться равной нулю.
Пусть это 4 последовательных числа: n, n + 1, n + 2, n + 3.
Тогда n (n + 1)(n + 2)(n + 3) + 1 = ( 2 + 3n)(n 2 + 3n + 2) + 1 = (n 2 + 3n) 2 + 2(n 2 + 3n) + 1 = (n 2 + 3n + 1) 2 .
Перенесем в левую часть 2sin4x · cos 4 x и прибавим и вычтем по cos 8 x.
В результате полученное уравнение можно преобразовать к виду (sin4x – cos 4 x) 2 + cos 2 x(1 – cos 6 x) = 0,
которое равносильно следующей системе:
Решая второе уравнение и подставляя его решения в первое уравнение,
в результате получим решение исходного уравнения x = π /2 + π k .
Пусть такой многогранник существует. Обозначим за 1, 2, …, число ребер на гранях,
тогда 1 + 2 + … – удвоенная сумма всех ребер многогранника, она – четная.
А в левой части стоит нечетная сумма слагаемых, каждое из которых – нечетно.
Получили противоречие. Значит, такого многогранника не существует.
Составим уравнение касательных к гиперболе в точке
Т. к.(1/x)’ = -1/(x 2 ), то эти уравнения будут иметь вид y = -1/(х 0 2 )(x — х 0 ) + 1/х 0 . (*)
Касательная с уравнением (*) пересекает ось абсцисс в точке (х 1 ;0);
х 1 можно определить из уравнения -1/(х 0 2 )(x — х 0 ) + 1/х 0 = 0.
Решая данное уравнение, получим х 1 = 2х 0 .
Точка (0; y 1 ) пересечения с осью ординат определяется подстановкой в уравнение (*) значения х = 0.
В итоге получим y 2 = 2/х 0 .
Отрезки осей координат и касательной составляют прямоугольный треугольник,
катеты которого имеют длины а = 2|х 0 | и b = 2 / |х 0 |.
Площадь данного треугольника равна 2.
Найдем произведение всех 25 чисел,
записанных под каждым столбцом и всех 25 чисел, записанных справа от строчек.
Так как в этом произведении каждое из чисел квадратной таблицы входит по два раза, то произведение этих 50 произведений, в каждом из которых стоит по 25 множителей, будет положительным, т. е. равно 1.
А так как произведение 50 чисел положительно, то отрицательных сомножителей будет четное число (2, 4, …, 50).
Сумма же 50 произведений может быть нулем лишь в случае, когда 25 слагаемых равно 1, а 25 слагаемых равно — 1, т. е. слагаемых с — 1 должно быть нечетное число.
А это значит, что сумма 50 написанных произведений не может равняться нулю.
Олимпиадные задания по математике 10-11 класс
олимпиадные задания по математике 10-11 класса с решениями для школьного тура.
Просмотр содержимого документа
«10 и 11 классы »
Задания школьной олимпиады по математике для 10 класса
2016 – 2017 учебный год
Докажите, что 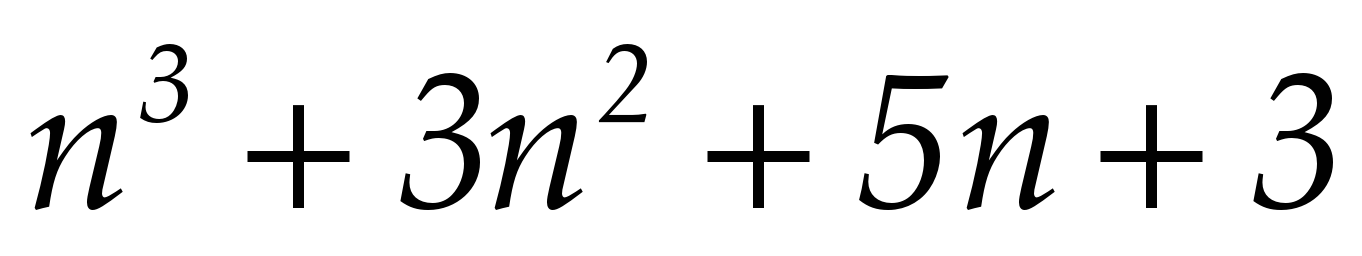
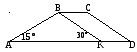
В трапеции ABCD длина основания AD равна 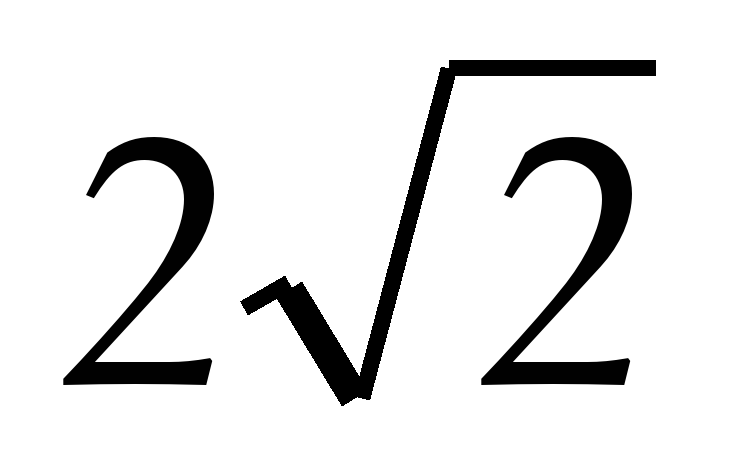
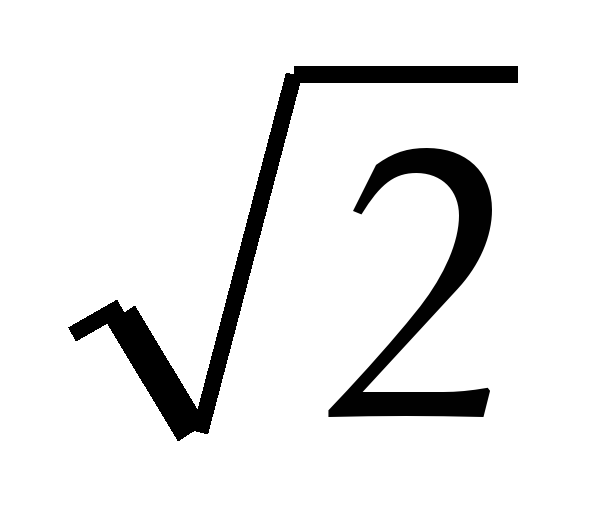
Какое наибольшее число натуральных слагаемых можно разложить число 96 так, чтобы все слагаемые были больше 1 и попарно взаимно просты?
Три подруги были в белом, красном и голубом платьях. Их туфли были так же трех цветов. Только у Тамары цвета платья и туфель совпадали. Валя была в белых туфлях. Ни платье, ни туфли Лиды не были красными. Определите цвет платья и туфель каждой из подруг.
Решить в целых числах систему уравнений
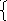
Задания школьной олимпиады по математике для 11 класса
2016 – 2017 учебный год
По дороге едут велосипедисты: на запад – Вася и Петя с равными между собой скоростями, а на восток – Коля и Миша с равными между собой скоростями. Вася встретился с Мишей в 12.00, Петя с Мишей – в 15.00, Вася с Колей – в 14.00. Когда встретились, Петя с Колей?
В мешке лежат 26 синих и красных шаров. Среди любых 18 шаров есть хотя бы один синий, а среди любых 10 шаров есть хотя бы один красный. Сколько красных шаров в мешке?
Морская вода содержит 5 процентов соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5 процентов.
Решите уравнение tgx ctgx ꞊ sin 5 x
В правильной треугольной пирамиде SABC с вершиной S SA/AB = 2. Проведены высота AD треугольника SAB и медиана BM треугольника ABC. Найдите отношение MD/BD.
Просмотр содержимого документа
«10 класс решение»
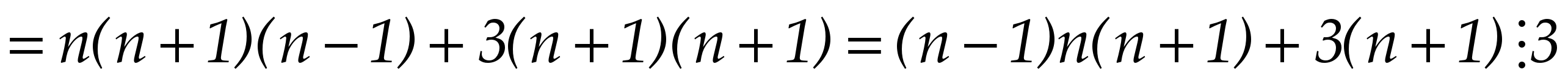
Проведем BK параллельно CD . Заметим KD || BC , KB || DC , следовательно, KBCD параллелограмм и KD = BC =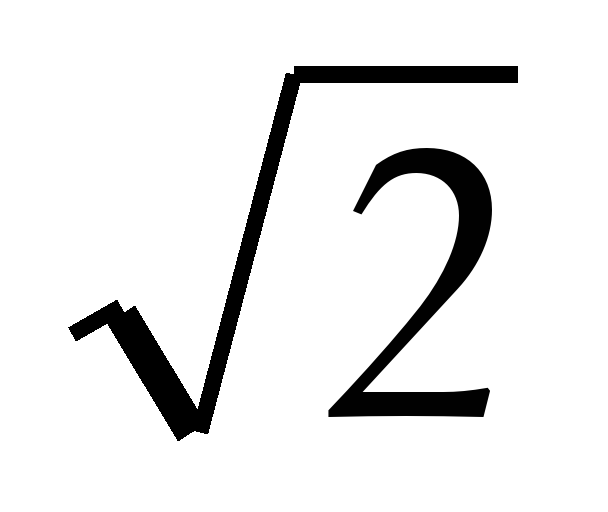
Далее найдем длину отрезка AK = AD – KD = 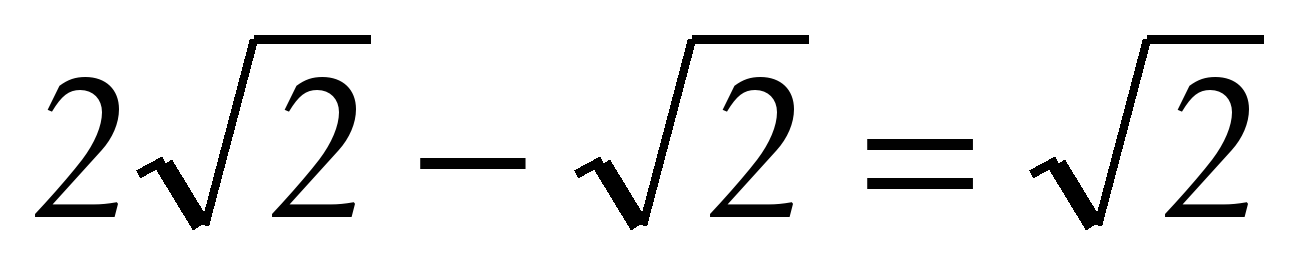
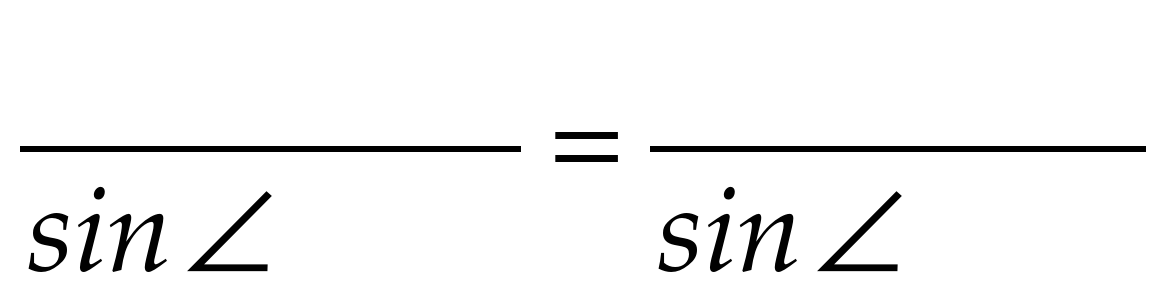
И sin 135° = 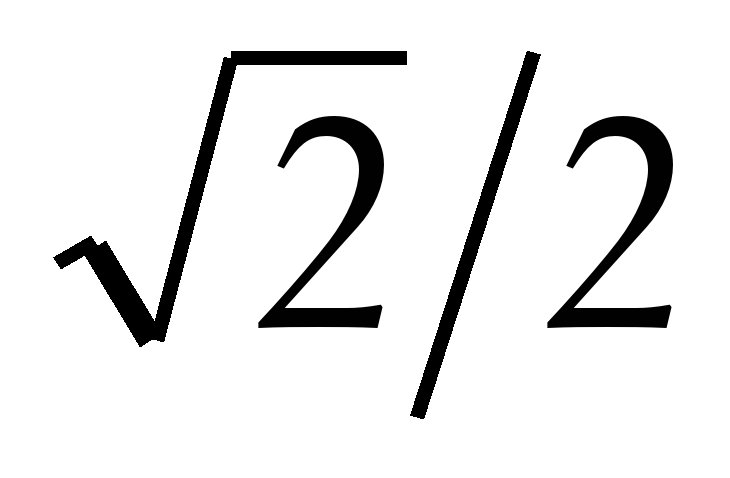
Ответ: на семь слагаемых.
Решение. Приведём пример разбиения числа 96 на семь слагаемых:
9 6 = 2 + 5 + 7 + 11 + 13 + 17 + 41.
Если слагаемых больше, то среди них не менее восьми нечётных (если их семь, то сумма нечётна). Заменим каждое из них на наименьший простой сомножитель. При этом сумма не увеличится, и все слагаемые будут различны. Но сумма восьми наименьших нечётных простых чисел равна 98.
Ответ: у Тамары были красные туфли и платье, у Вали – белые туфли и голубое платье, у Лиды – белое платье и голубые туфли.
Ответ: х = 95, у = 0, z = 94 или х = 31, у = 2, z = 32.
Решение. Вычтя из второго уравнения первое, получим (х — z)(1 — у) = 1.
По условию, х, у, z целые, тогда возможны два случая:
1) х– z = 1, 1 – у = 1, т. е. у = 0. Подставив значение у в систему, получим: z =94, x =95.
2) х – z = -1, 1 – у = — 1, т. е. z = х +1, у = 2. Подставим найденные значения у и z в первое уравнение, получим 2х + х +1 = 94, х = 31. Отсюда z = 32 .
Просмотр содержимого документа
«11 класс решение»
Решение. Расстояние между Мишей и Колей и их скорости не меняются, а скорости Васи и Пети равны. Вася встретил Колю через 2 часа после Миши, значит, Петя встретят Колю тоже через 2 часа после Миши, т. е. в 17.00.
Решение. Так как из 18 шаров найдется хотя бы один синий, то красных не более 17, а из любых 10 шаров найдется хотя бы один красный, то есть синих не более 9. Так как всех шаров 26, то синих – 9, а красных – 17.
Решение. 5 процентов от 30 кг — 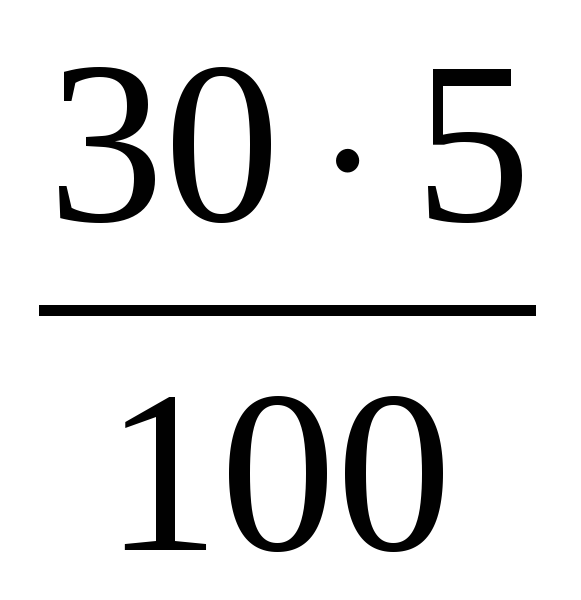
Х л добавили, стало (х+30)л. Х+30-100 процентов, 1,5 -1,5 процентов, тогда х=70
Ответ: 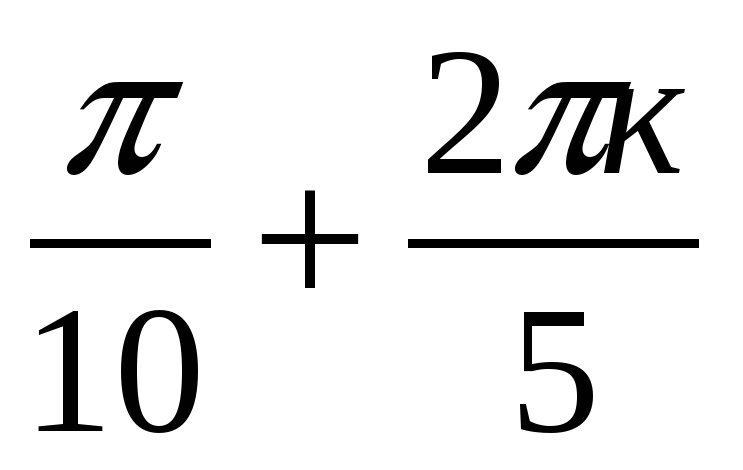

Решение. tgx ctgx ꞊ sin 5 x
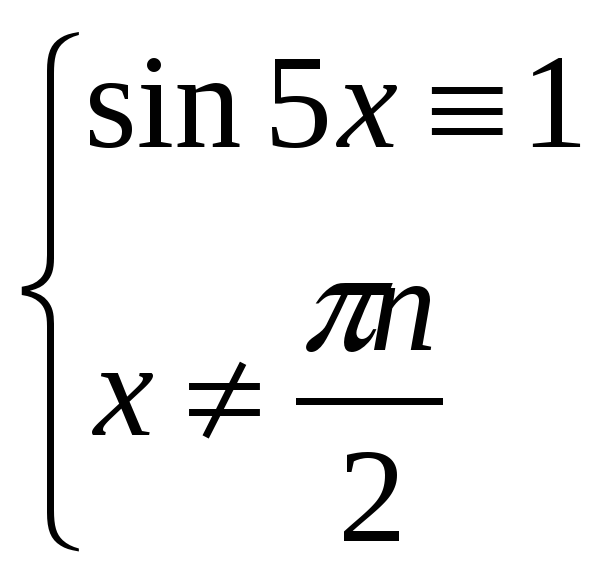
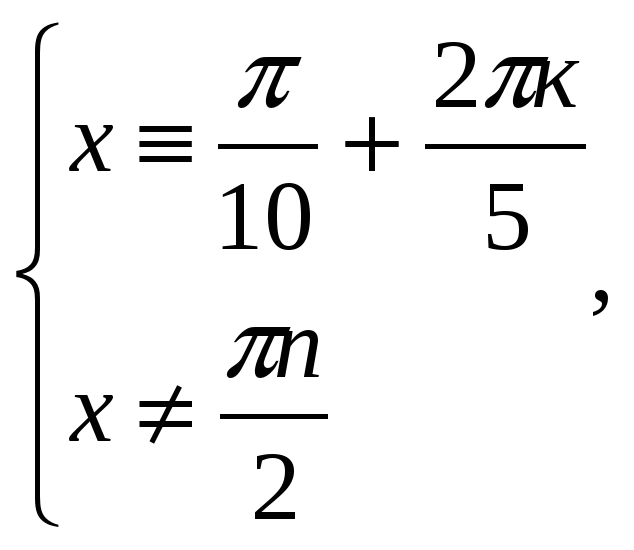


Найдем теперь такие k , при которых 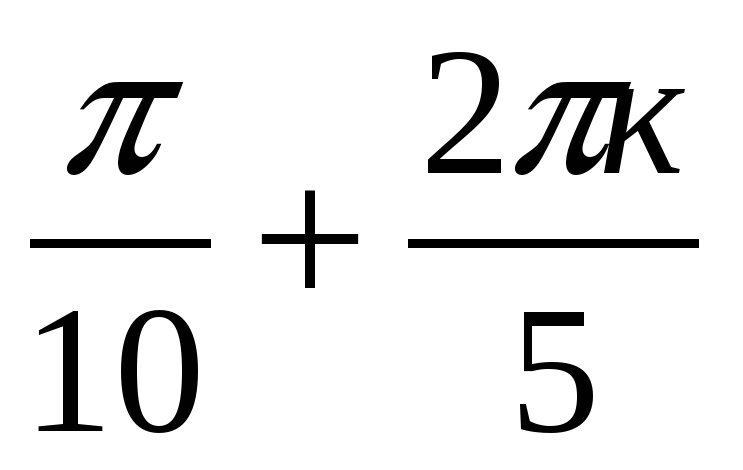
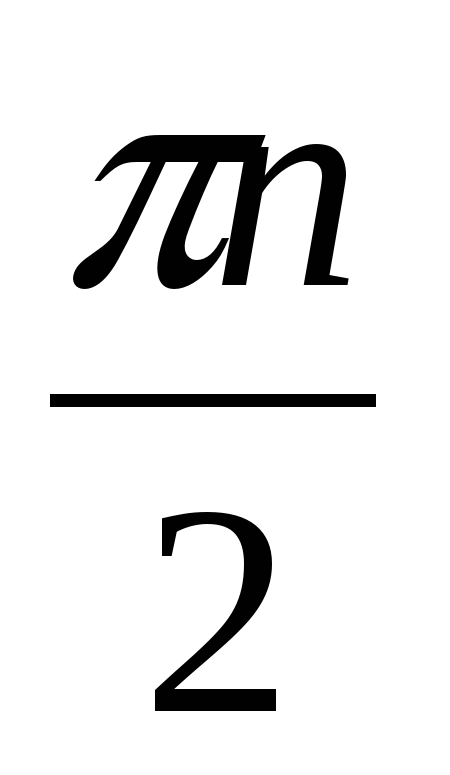
n 0꞊1, k 0꞊1,тогда k ꞊1+5 t , t
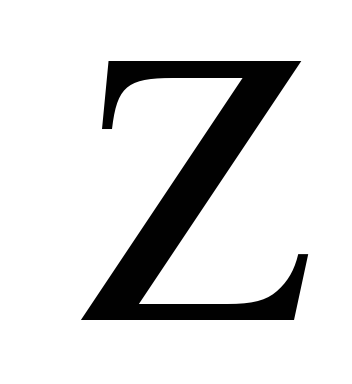
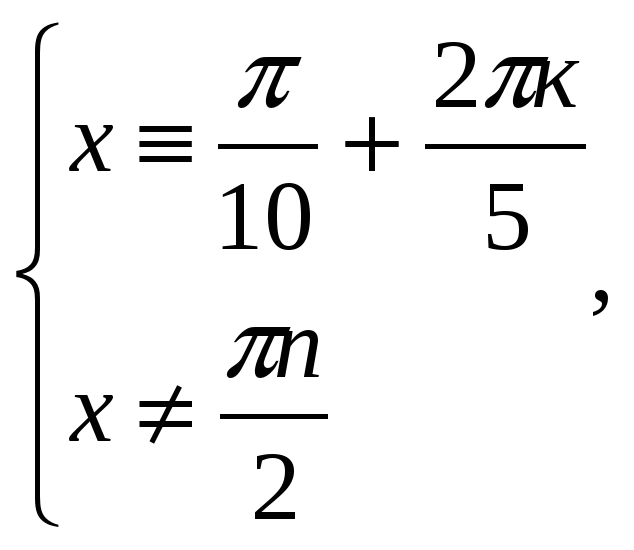
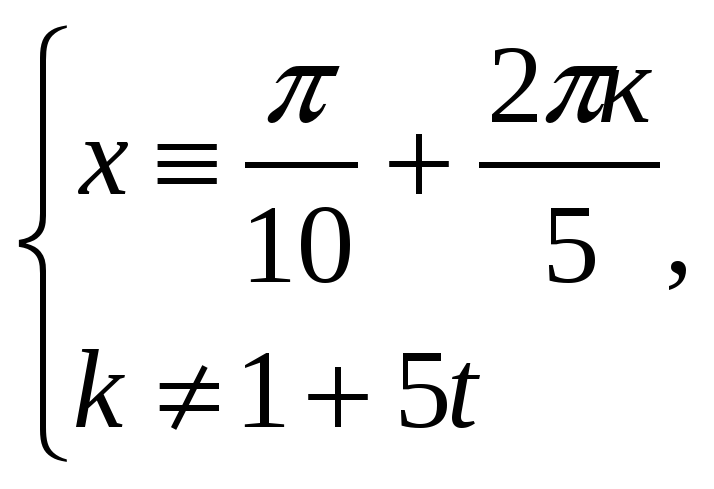

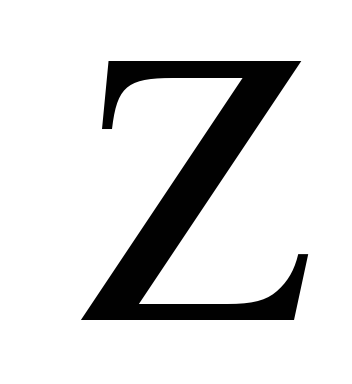

Ответ:
Решение. Обозначим длину отрезка AB за 1, тогда SA=2. Найдём прежде всего длины отрезков BD и SD. Пусть BD=x. Тогда, применяя теорему Пифагора к треугольникам ABD и ASD, получаем AD²=1–x² = 4 – (2–x)², BD=x=1/2. Далее в треугольнике BMD BM꞊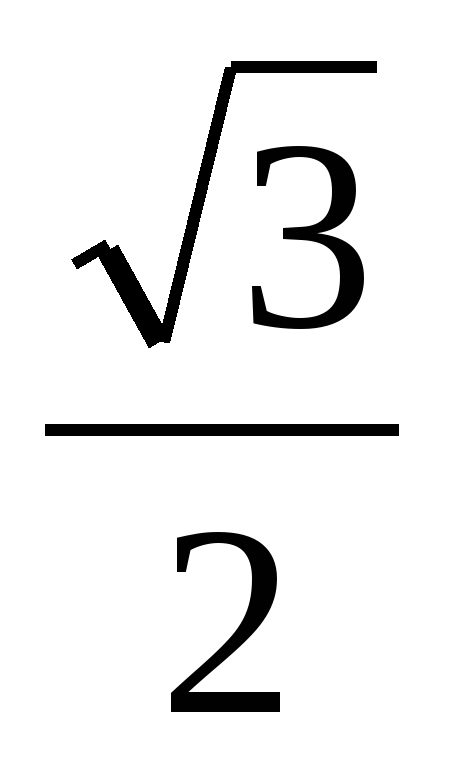
DM ² ꞊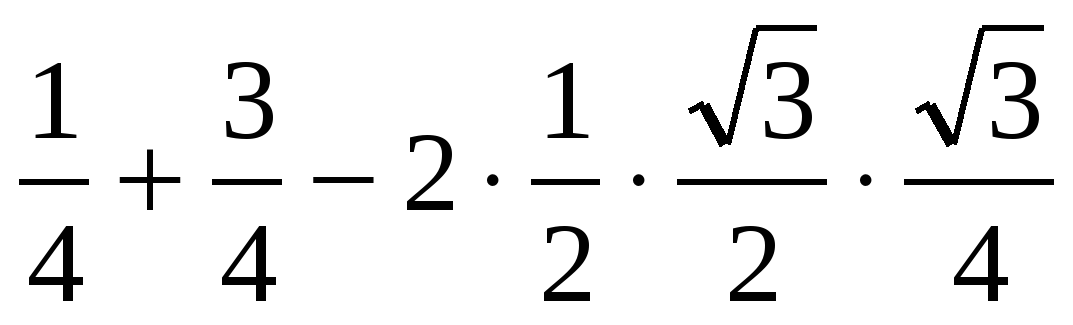
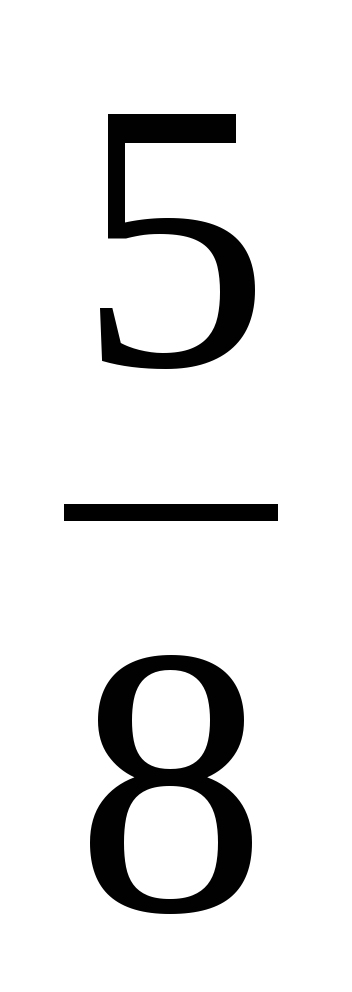
http://nsportal.ru/shkola/matematika/library/2019/03/18/olimpiadnye-zadaniya-po-matematike-dlya-11-klassa-s-resheniem
http://multiurok.ru/files/olimpiadnyie-zadaniia-po-matiematikie-10-11-klass.html