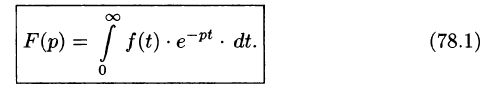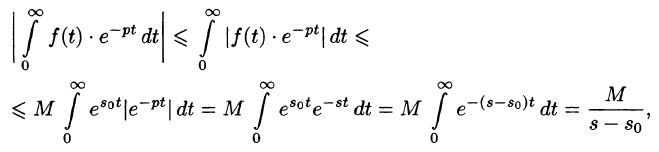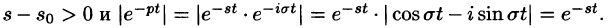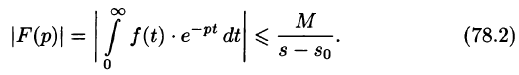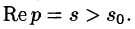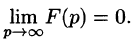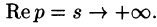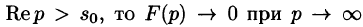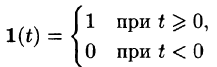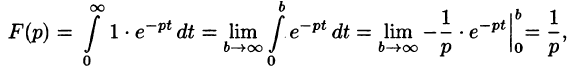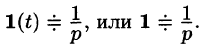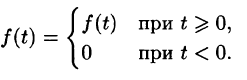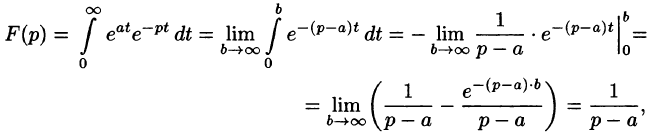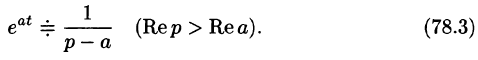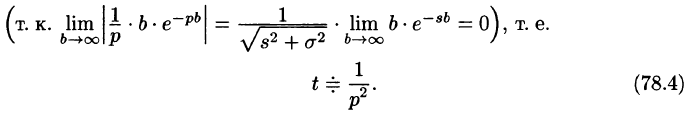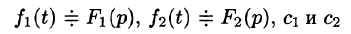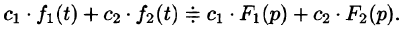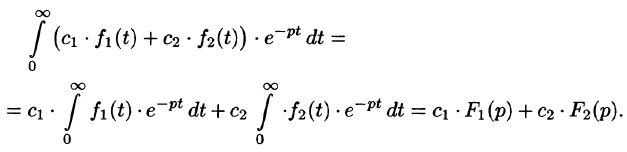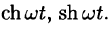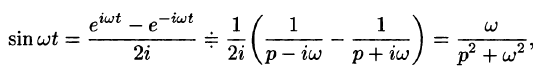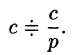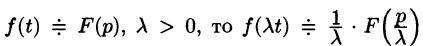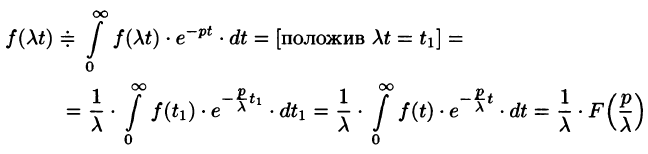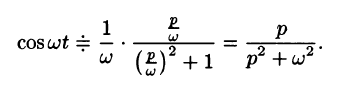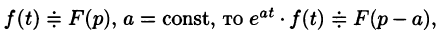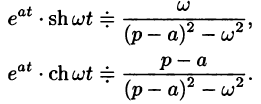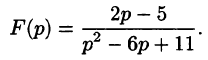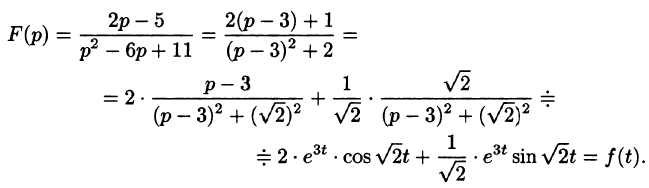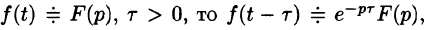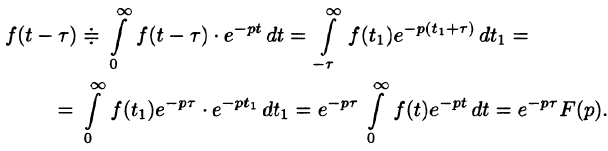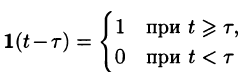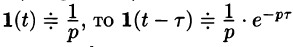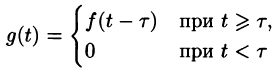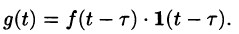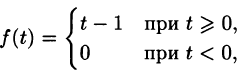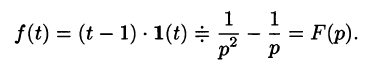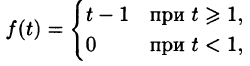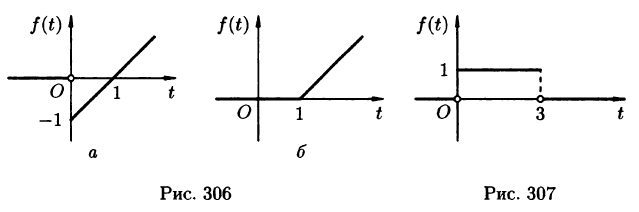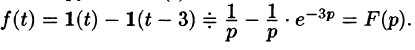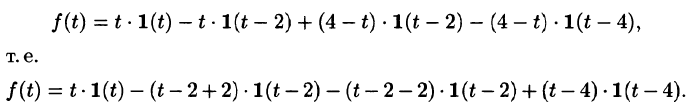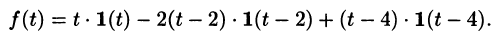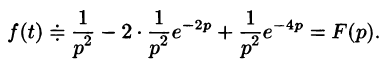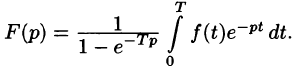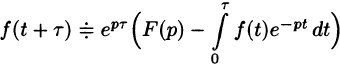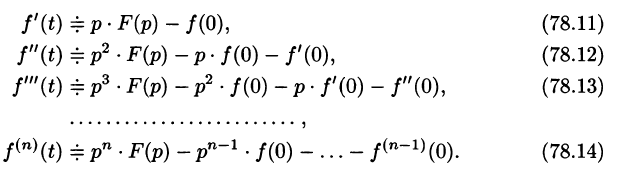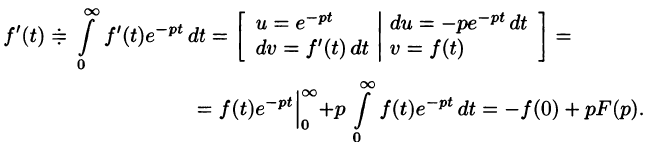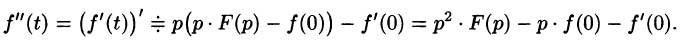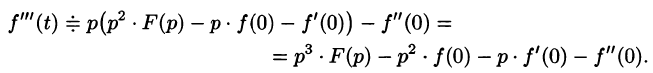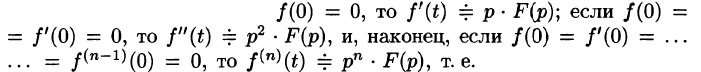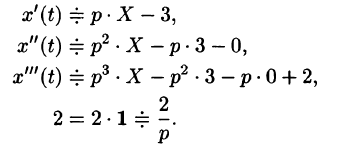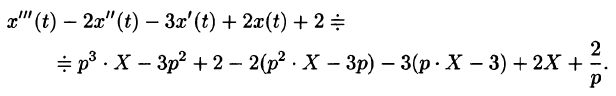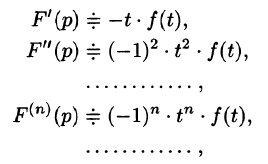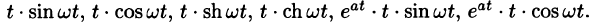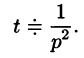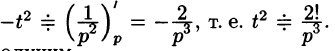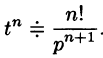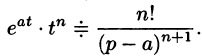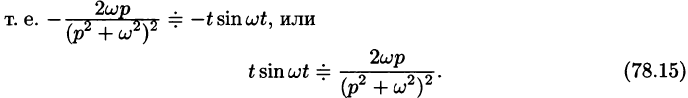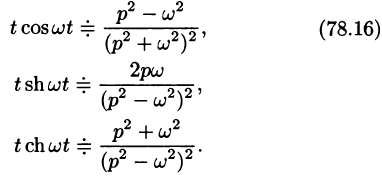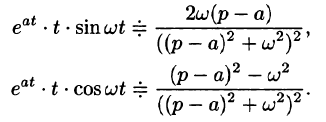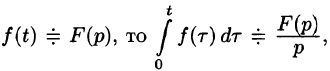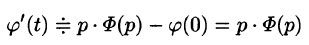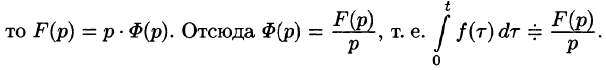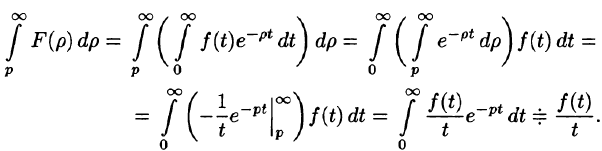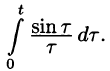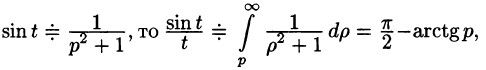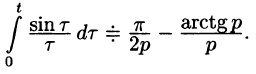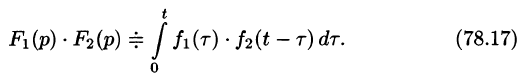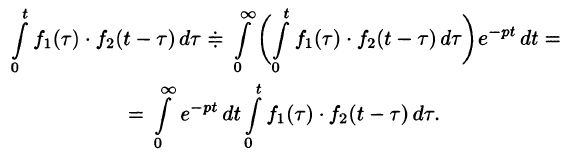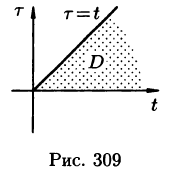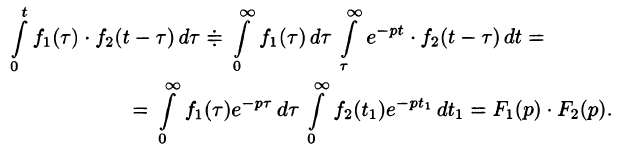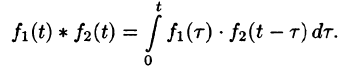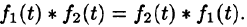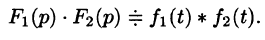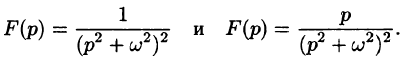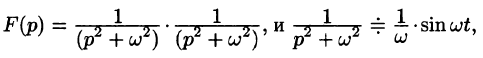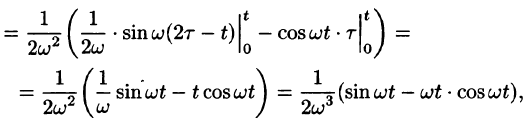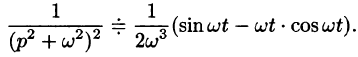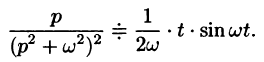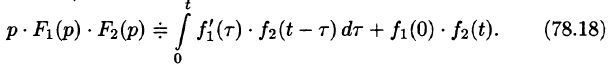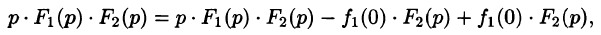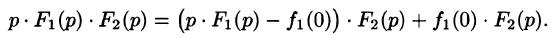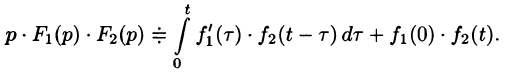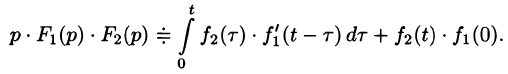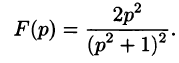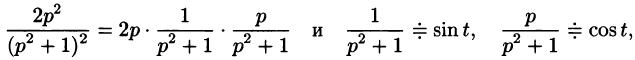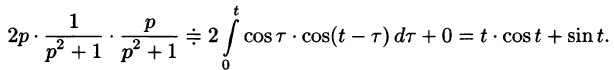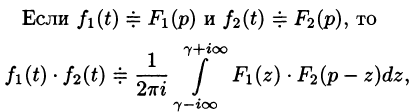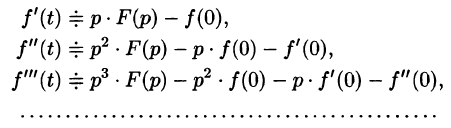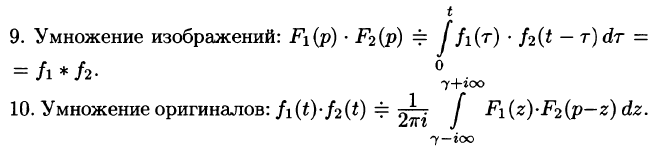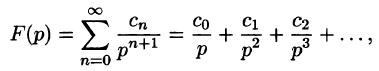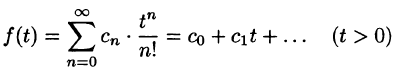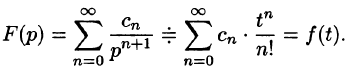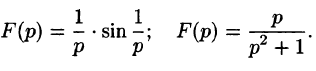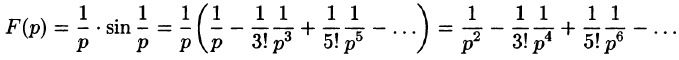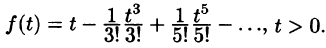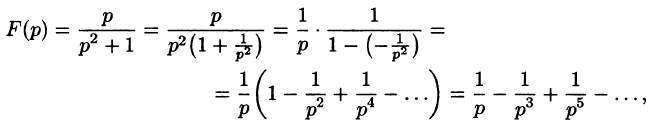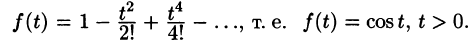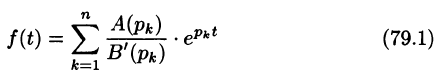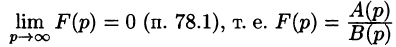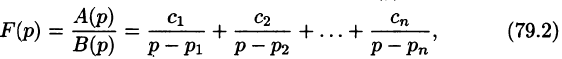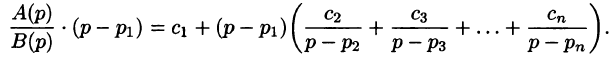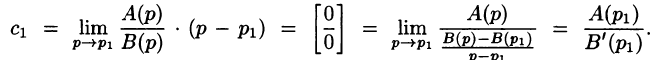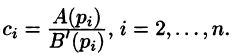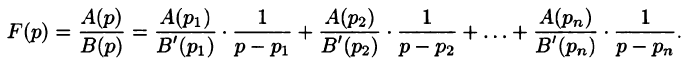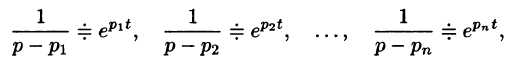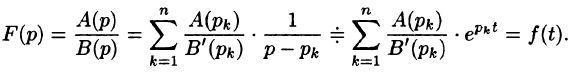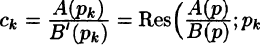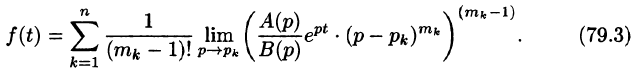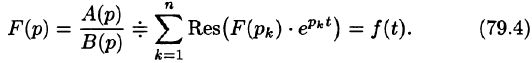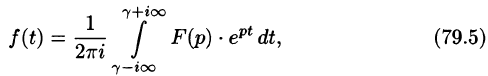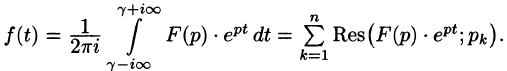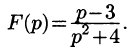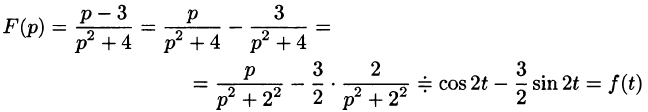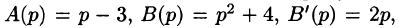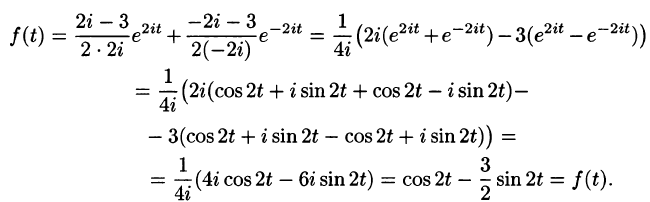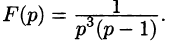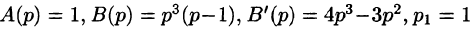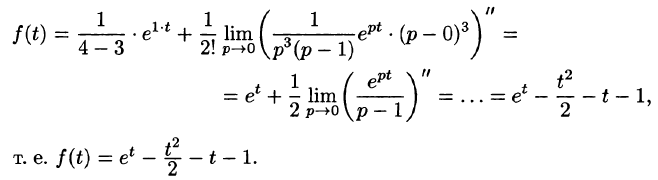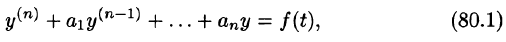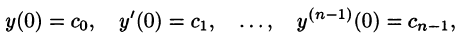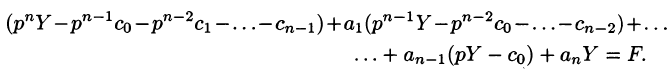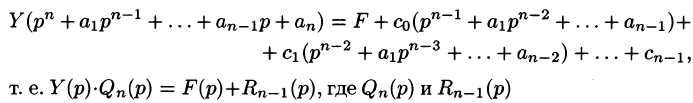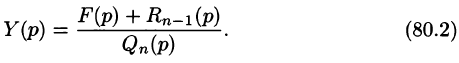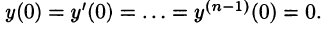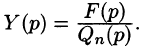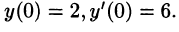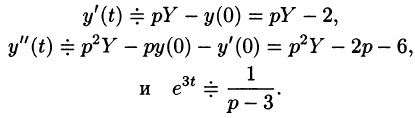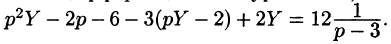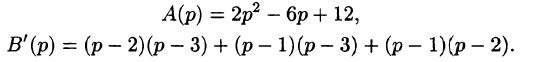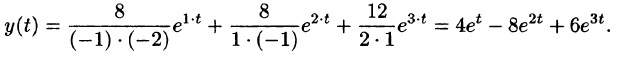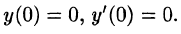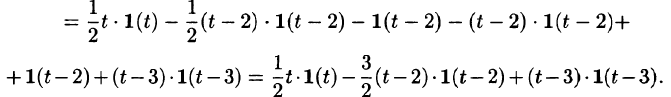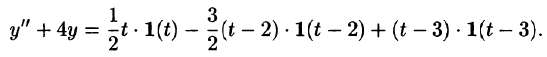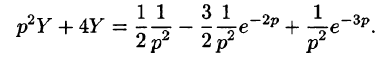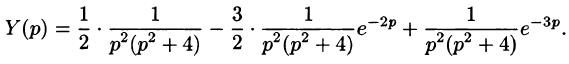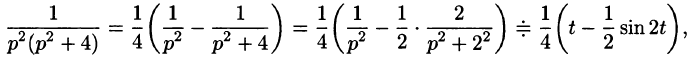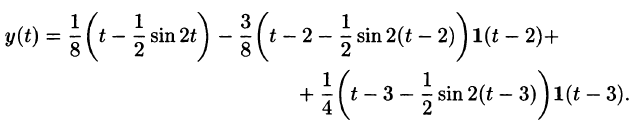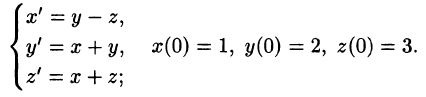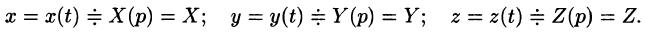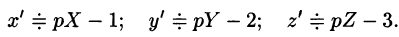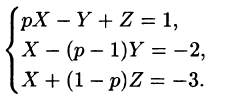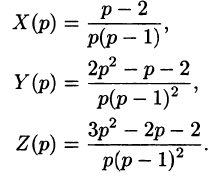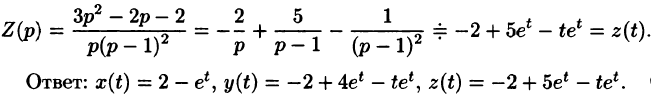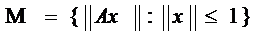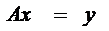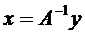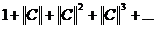Операционное исчисление с примерами решения и образцами выполнения
Операционное исчисление играет важную роль при решении прикладных задач, особенно в современной автоматике и телемеханике.
Операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев сводить исследование дифференциальных и некоторых типов интегральных операторов и решение уравнений, содержащих эти операторы, к рассмотрению более простых алгебраических задач.
Методы операционного исчисления предполагают реализацию следующей условной схемы решения задачи.
- От искомых функций переходят к некоторым другим функциям — их изображениям.
- Над изображениями производят операции, соответствующие заданным операциям над самими функциями.
- Получив некоторый результат при действиях над изображениями, возвращаются к самим функциям.
В качестве преобразования, позволяющего перейти от функции к их изображениям, будем применять так называемое преобразование Лапласа.
Преобразование Лапласа
Оригиналы и их изображения:
Основными первоначальными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть f(t) — действительная функция действительного переменного t (под t будем понимать время или координату).
Функция f(t) называется оригиналом, если она удовлетворяет следующим условиям:
- f(t)— кусочно-непрерывная при
т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
- Существуют такие числа
что для всех t выполняется неравенство
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число
называется показателем роста f(t).
Условия 1-3 выполняются для большинства функций, описывающих различные физические процессы.
Первое условие означает, что процесс начинается с некоторого момента времени; удобнее считать, что в момент t = 0. Третьему условию удовлетворяют ограниченные функции (для них можно положить 
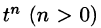
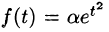
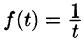
Замечание:
Функция f(t) может быть и комплексной функцией действительно переменного, т. е. иметь вид 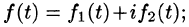
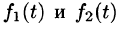
Изображением оригинала f(t) называется функция F(p) комплексного переменного 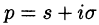
Операцию перехода от оригинала f(t) к изображению F(p) называют преобразованием Лапласа. Соответствие между оригиналом f(t) и изображением F(p) записывается в виде 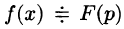
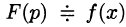
Теорема:
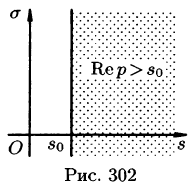
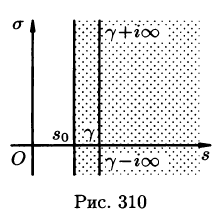
Существование изображения. Для всякого оригинала f(t) изображение F(p) существует (определено) в полуплоскости 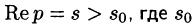
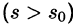
Докажем первую часть теоремы. Пусть 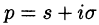
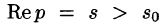
Учитывая, что 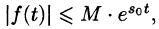
Отсюда вытекает абсолютная сходимость интеграла (78.1), т. е. изображение F(p) существует и однозначно в полуплоскости
Следствие:
Необходимый признак существования изображения. Если функция F(p) является изображением функции f(t) , то
Это утверждение непосредственно вытекает из неравенства (78.2), когда
Так как F(p) — аналитическая функция в полуплоскости
по любому направлению. Отсюда, в частности, следует, что функции 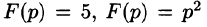
Отметим, что из аналитичности функции F(p) следует, что все ее особые точки должны лежать левее прямой 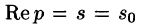
Теорема:
О единственности оригинала. Если функция F(p) служит изображением двух оригиналов 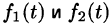
(Примем без доказательства.)
Пример:
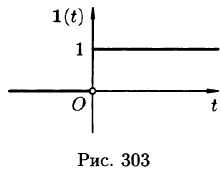
Найти изображение единичной функции Хевисайда
Решение:
По формуле (78.1) при 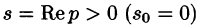
т. e. 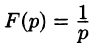
В дальнейшем функцию-оригинал будем кратко записывать в виде f(t) , подразумевал, что
Пример:
Найти изображение функции 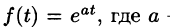
Решение:
Данная функция является оригиналом. По формуле (78.1) имеем
если Re(p — a) > 0. Таким образом,
Пример:
Найти изображение функции f(t) = t.
Решение:
В этом случае преобразование Лапласа имеет вид
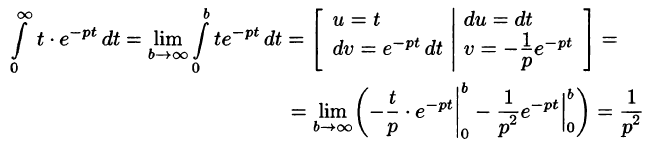
Замечание:
Функция 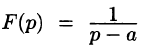
Свойства преобразования Лапласа
Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. Свойства преобразования Лапласа существенно облегчают задачу нахождения изображений для большого числа разнообразных функций, а также задачу отыскания оригиналов по их изображениям.
Линейность
Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т. е. если
— постоянные числа, то
Используя свойства интеграла, находим
Пример:
Найти изображения функций 
Решение:
Пользуясь свойством линейности, формулой (78.3), находим:
Аналогично получаем формулу
Далее, 
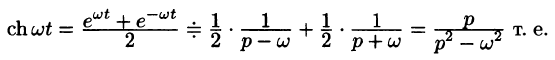
Аналогично получаем формулу
т.е. умножение аргумента оригинала на положительное число 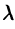
По формуле (78.1) имеем
(так как безразлично, какой буквой обозначена переменная интегрирования).
Например, пусть 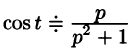
Смещение (затухание)
т. е. умножение оригинала на функцию 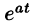
В силу формулы (78.1) имеем
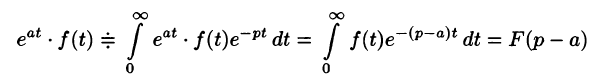
Благодаря этому свойству можно расширить таблицу соответствия между оригиналами и их изображениями:
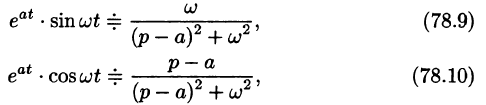
Пример:
Найти оригинал по его изображению
Решение:
Преобразуем данную дробь так, чтобы можно было воспользоваться свойством смещения:
(См. формулы (78.9), (78.10) и свойство линейности.)
Запаздывание
т. е. запаздывание оригинала на положительную величину 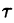
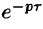
Положив 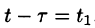
Поясним термин «запаздывание». Графики функции f(t) и 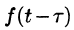
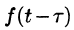
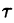
Рис. 304
Рис. 305
вправо (см. рис. 304). Следовательно, функции f(t) и 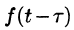
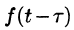
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями; функций, описывающих импульсные процессы.
называется обобщенной единично ной функцией (см. рис 305).
можно записать так:
Пример:
Найти изображение f(t) = t — 1.
Решение:
Для того чтобы быть оригиналом, функция f(t) должна удовлетворять условиям 1-3 (см. п. 78.1). В этом смысле исходную задачу можно понимать двояко.
Если понимать функцию f(t) как
т. е. 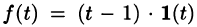
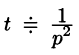
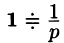
Если же понимать функцию f(t) как
т. е. 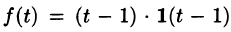
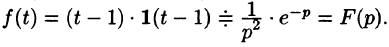
Пример:
Найти изображение функции
Решение:
Данная функция описывает единичный импульс (см. рис. 307), который можно рассматривать как разность двух оригиналов: единичной функции 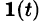
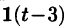
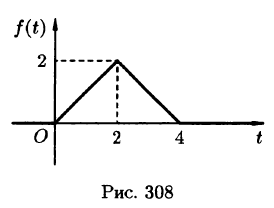
Пример:
Найти изображение функции

Решение:
Функция-оригинал изображена на рис. 308. Запишем ее одним аналитическим выражением, используя функции Хевисайда 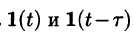
Раскроем скобки и приведем подобные слагаемые:
Изображение функции f(t) будет равно
Замечания:
1.Изображение периодического оригинала с периодом, равным Т,
есть
применяется значительно реже.
Дифференцирование оригинала
Если 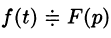
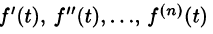
По определению изображения находим
Итак, 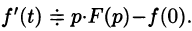
Аналогично найдем изображение третьей производной f»‘(t):
Применяя формулу (78.11) (п — 1) раз, получим формулу (78.14).
Замечание. Формулы (78.11)-(78.14) просто выглядят при нулевых начальных условиях: если
т. е. дифференцированию оригинала соответствует умножение его изображения на р.
Рассмотренное свойство дифференцирования оригинала вместе со свойством линейности широко используется при решении линейных дифференциальных уравнений.
Пример:
Найти изображение выражения
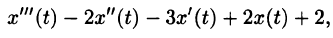
Решение:
Пусть 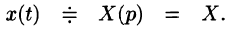
Дифференцирование изображения
Если 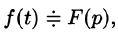
т. е. дифференцированию изображения соответствует умножение его оригинала на (-t).
Согласно теореме 78.1 существования изображения, F(p) является аналитической функцией в полуплоскости 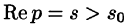
Пример:
Найти изображения функций
Решение:
Так как 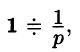
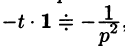
Продолжая дифференцирование, получим
С учетом свойства смещения получаем
Согласно формуле (78.5), 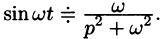
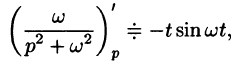
Аналогично, используя формулы (78.6), (78.7) и (78.8), находим
С учетом свойства смещения и формул (78.15) и (78.16), получаем
Интегрирование оригинала
т. е. интегрированию оригинала от 0 до t соответствует деление его изображения на р.
Функция 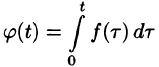
Пусть 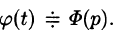
(так как 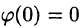
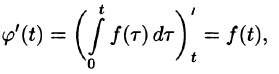
Интегрирование изображения
Если 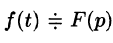
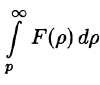
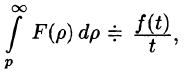
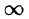
Используя формулу (78.1) и изменяя порядок интегрирования (обоснование законности этой операции опускаем), получаем
Пример:
Найти изображение функции 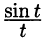
Решение:
т. е. 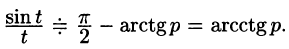
Умножение изображений
Если 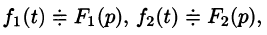
Можно показать, что функция 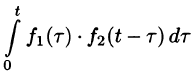
Используя преобразование Лапласа (78.1), можно записать
Область D интегрирования полученного двукратного интеграла определяется условиями 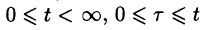
Изменяя порядок интегрирования и полагая 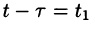
Интеграл в правой части формулы (78.17) называется сверткой функции 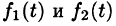
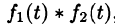
Можно убедиться (положив 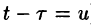
Умножение изображений соответствует свертыванию их оригиналов, т. е.
Пример:
Найти оригинал функций
Решение:
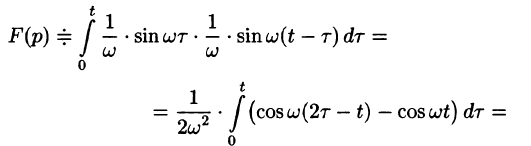
Следствие:
Если 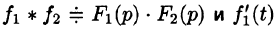
Запишем произведение 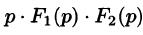
Первое слагаемое в правой части есть произведение изображений, соответствующих оригиналам 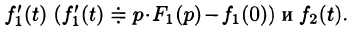
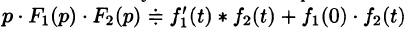
Формула (78.18) называется формулой Дюамеля. На основании свойства переместительности свертки формулу Дюамеля можно записать в виде
Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
Пример:
Найти оригинал, соответствующий изображению
Решение:
то на основании формулы Дюамеля (78.18) имеем
Умножение оригиналов
где путь интегрирования — вертикальная прямая 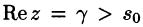
Рассмотренные свойства преобразования Лапласа представляют собой основные правила (аппарат) операционного исчисления. Для удобства пользования перечислим эти свойства.
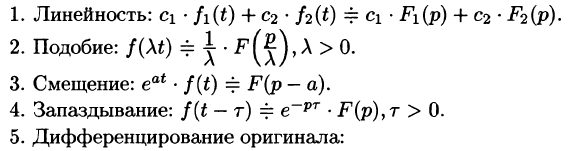
6. Дифференцирование изображения
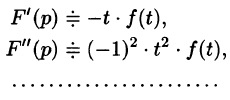
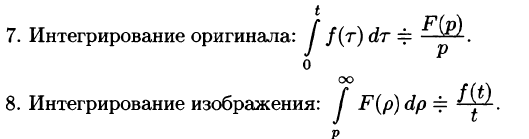
Таблица оригиналов и изображений
Составим краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями. Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В. А. Диткин и П. И. Кузнецов).


Обратное преобразование Лапласа
Теоремы разложения:
Рассмотрим две теоремы, называемые теоремами разложения, позволяющие по заданному изображению F(p) находить соответствующий ему оригинал f(t).
Теорема:
Если функция F(p) в окрестности точки 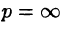
является оригиналом, имеющим изображение F(p), т. е.
Примем эту теорему без доказательства.
Пример:
Найти оригинал f(t), если
Решение:
Следовательно, на основании теоремы 79.1
Запишем лорановское разложение функции 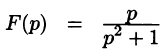
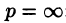
где 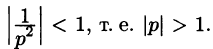
Теорема:
Если 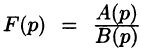
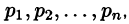
является оригиналом, имеющим изображение F(p).
Отметим, что дробь 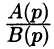
не может быть изображением.
Разложим правильную рациональную дробь 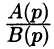
где 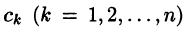
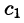
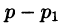
Переходя в этом равенстве к пределу при 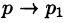
Итак, 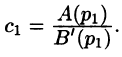
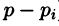
Подставляя найденные значения 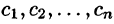
Так как по формуле (78.3)
то на основании свойства линейности имеем
Замечание:
Легко заметить, что коэффициенты 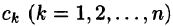
Можно показать, что если 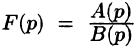
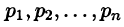
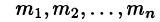
Теорему 79.2 можно сформулировать следующим образом:
Теорема:
Если изображение 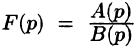
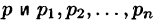
Формула Римана-Меллина
Общий способ определения оригинала по изображению дает обратное преобразование Лапласа (формула обращения Римана-Меллина), имеющее вид
где интеграл берется вдоль любой прямой 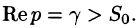
При определенных условиях интеграл (79.5) вычисляется по формуле
Замечание:
На практике отыскание функции-оригинала обычно проводят по следующему плану: прежде всего следует по таблице оригиналов и изображений попытаться отыскать для заданного изображения F(p) соответствующий ему оригинал; второй путь состоит в том, что функцию F(p) стараются представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности, найти оригинал; наконец, использовать теоремы разложения, свойство умножения изображений, формулу обращения и т.д.
Пример:
Найти оригинал по его изображению
Решение:
Проще всего поступить так:
(использовали свойство линейности и формулы (78.5) и (78.6)).
Если же использовать теорему 79.2 разложения, то будем иметь:
корни знаменателя 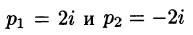
Пример:
Найти функцию-оригинал, если ее изображение
задано как
Решение:
— простой корень знаменателя, 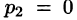
Приведем другой способ нахождения f(t). Разобьем дробь
на сумму простейших дробей:
Приведем третий способ нахождения f(t). Представим F(p) как
произведение 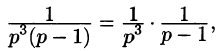
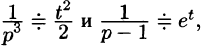
Операционный метод решения линейных дифференциальных уравнений и их систем
Пусть требуется найти частное решение линейного дифференциального уравнения с постоянными коэффициентами
удовлетворяющее начальным условиям
где 
Будем считать, что искомая функция y(t) вместе с ее рассматриваемыми производными и функция f(t) являются оригиналами.
Пусть 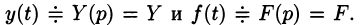
Полученное уравнение называют операторным (или уравнением в изображениях). Разрешим его относительно Y:
— алгебраические многочлены от p степени п и п-1 соответственно. Из последнего уравнения находим
Полученное равенство называют операторным решением дифференциального уравнения (80.1). Оно имеет более простой вид, если все начальные условия равны нулю, т. е.
В этом случае
Находя оригинал y(t), соответствующий найденному изображению (80.2), получаем, в силу теоремы единственности, частное решение дифференциального уравнения (80.1).
Замечание:
Полученное решение y(t) во многих случаях оказывается справедливым при всех значениях t (а не только при 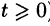
Пример:
Решить операционным методом дифференциальное уравнение 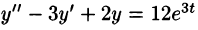
Решение:
Пусть 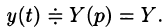
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:
Отсюда 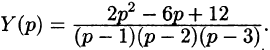
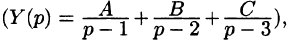
Пример:
Найти решение уравнения
при условии
Решение:
График данной функции имеет вид, изображенный на рисунке 311.
С помощью единичной функции правую часть данного дифференциального уравнения можно записать одним аналитическим выражением:
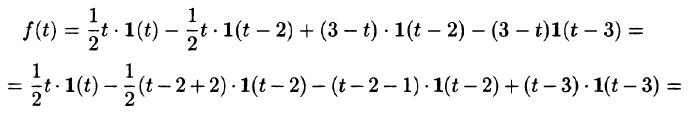
Таким образом, имеем
Операторное уравнение, при нулевых начальных условиях имеет вид
то по теореме запаздывания находим:
Аналогично применяется операционный метод для решения систем линейных дифференциальных уравнений с постоянными коэффициентами.
Покажем это на конкретном примере.
Пример:
Решить систему дифференциальных уравнений
Решение:
Система операторных уравнений принимает вид
Решая эту систему алгебраических уравнений, находим:
Переходя от изображений к оригиналам, получаем искомые решения:
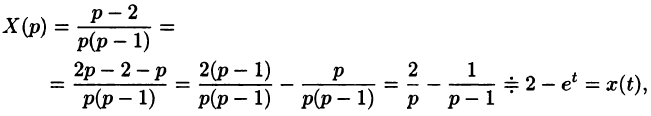
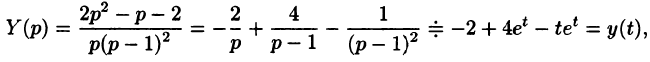
С помощью операционного исчисления можно также находить решения линейных дифференциальных уравнений с переменными коэффициентами, уравнений в частных производных, уравнений в конечных разностях (разностных уравнений); производить суммирование рядов; вычислять интегралы. При этом решение этих и других задач значительно упрощается.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Операторные уравнения и методы их решения
Сущность операторного метода заключается в том, что функции 


Изображение 

 . . | (1) |
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:

Следует отметить, что если оригинал 

В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Оригинал  | Изображение  |
| A |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Некоторые свойства изображений
- Изображение суммы функций равно сумме изображений слагаемых:


С использованием этих свойств и данных табл. 1, можно показать, например, что

Изображения производной и интеграла
В курсе математики доказывается, что если 



Таким образом, для напряжения на индуктивном элементе можно записать
или при нулевых начальных условиях

Отсюда операторное сопротивление катушки индуктивности

Аналогично для интеграла: если 

С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:

или при нулевых начальных условиях

откуда операторное сопротивление конденсатора

Закон Ома в операторной форме
Пусть имеем некоторую ветвь 
сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.
Для мгновенных значений переменных можно записать:

Тогда на основании приведенных выше соотношений получим:

 , , | (2) |
где 
Следует обратить внимание, что операторное сопротивление 


Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения, представленную на рис. 2.
Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю

Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура

При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде

В качестве примера запишем выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 — 

В первом случае в соответствии с законом Ома 
Во втором случае, т.е. при 
откуда 


Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа

которое представляет собой решение интегрального уравнения (1) и сокращенно записывается, как:

На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала.
Например, для изображения тока в цепи на рис. 5 можно записать

Тогда в соответствии с данными табл. 1

что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение 

где 
Это выражение может быть представлено в виде суммы простых дробей
 , , | (3) |
где 

Для определения коэффициентов 


При

Рассматривая полученную неопределенность типа 


Поскольку отношение 

 . . | (4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней уравнения 


В заключение раздела отметим, что для нахождения начального 

которые также могут служить для оценки правильности полученного изображения.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- В чем заключается сущность расчета переходных процессов операторным методом?
- Что такое операторная схема замещения?
- Как при расчете операторным методом учитываются ненулевые независимые начальные условия?
- Какими способами на практике осуществляется переход от изображения к оригиналу?
- Для чего используются предельные соотношения?
- Как связаны изображение и оригинал в формуле разложения? Какие имеются варианты ее написания?
С использованием теоремы об активном двухполюснике записать операторное изображение для тока через катушку индуктивности в цепи на рис. 6.
Ответ: 
С использованием предельных соотношений и решения предыдущей задачи найти начальное и конечное значения тока в ветви с индуктивным элементом.
Ответ: 
Операторные уравнения
Выпускная квалификационная работа
Выполнила студентка V курса математического факультета Кощеева Анна Сергеевна
Вятский Государственный Гуманитарный университет (ВятГГУ)
Функциональный анализ – мощное средство для решения математический задач, возникающих в реальных ситуациях, он имеет множество приложений в различных областях математики, его методы проникают в смежные технические дисциплины.
Многие задачи математической физики, теории упругости, гидродинамики сводятся к отысканию решения дифференциального линейного уравнения, что, в свою очередь, приводит к задаче отыскания решения уравнения Аx = y с линейным оператором А. В данной работе рассмотрены два метода решения операторных уравнений.
Цель данной работы: рассмотреть основы теории линейных операторов и методы решения операторных уравнений – метод малого параметра и метод продолжения по параметру, показать применение этих методов к решению задач.
Изучив имеющийся материал по данной теме, я поставила перед собой следующие задачи:
раскрыть некоторые основы теории линейных операторов, необходимые для освоения методов решения операторных уравнений;
проиллюстрировать на конкретных примерах способы решения операторных уравнений и дать пояснения по ходу решения конкретных задач.
Так как выделение из функционального анализа его прикладной части, содержащей конструктивные методы получения решений задач, преследует методическую цель – сделать эти методы доступнее тем, кто занимается приложениями математики. Поэтому данная работа разделена на две главы, в первой содержатся необходимые теоретические обоснования способов решения операторных уравнений и суть обоих методов, а во второй – решения конкретных задач.
Глава 1. Операторные уравнения
§1.Определение линейного оператора
Пусть X и Y – линейные пространства, оба вещественные или оба комплексные.
Оператор А: X → Y с областью определения D(А) называется линейным, если
А(λ1×1 + λ2×2) = λ1А(x1) + λ2А(x2)
для любых x1,x2 Î D и любых скаляров λ1 и λ2.
Пусть X и Y – нормированные пространства и А: X → Y, где А – линейный оператор, всюду заданный в X (т.е. D(А) = X).
Оператор А называется непрерывным в точке x0 Î X, если Аx → Аx0 при x → x0. Но судить о непрерывности линейного оператора в различных точках x0 Î X можно по непрерывности его в нуле пространства X.
Теорема 1. Пусть линейный оператор А всюду задан в банаховом пространстве X и со значениями в банаховом пространстве Y непрерывен в точке 0 Î X; тогда А непрерывен в любой точке x0 Î X.
Доказательство. Рассмотрим равенство Аx – Аx0 = А (x – x0). Если x → x0, то z = x – x0 → 0. По непрерывности в нуле Аz → 0, но тогда Аx – Аx0 → 0, что и требовалось доказать.
Линейный оператор А называется непрерывным, если он непрерывен в точке x = 0.
Пусть S1(0) – замкнутый шар ||x|| ≤ 1 в банаховом пространстве X.
Будем называть линейный оператор А: X → Y ограниченным, если он ограничен на единичным шаре S1(0), т.е. если ограничено множество
Согласно определению, если А ограничен, то существует постоянная с > 0 такая, что для любых x с ||x|| ≤ 1 справедливо неравенство
Теорема 2. А ограничен тогда и только тогда, когда справедлива оценка
для любых x Î X, где с – постоянная.
Теорема 3. Пусть А: X → Y, А – линейный оператор, X, Y – банаховы пространства. Для того чтобы А был непрерывным, необходимо и достаточно, чтобы он был ограниченным.
§2. Норма линейного оператора
В линейном пространстве непрерывных линейных операторов зададим норму следующим образом:
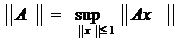
Поясним, почему существует конечное число ||А||, определяемое для любого ограниченного оператора равенством (1). Так как А – ограничен, то множество
ограничено сверху. По теореме о верхней грани существует 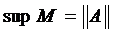
Из свойства sup M следует, что ||Аx|| ≤ ||А|| для всех x Î S1(0). Отсюда
справедливое для всех x Î X, включая x = 0. таким образом, ||А|| является наименьшей из констант в неравенстве ||Аx|| ≤ ||А||, и, значит, оценка (2) является наилучшей.
Пространство нормированных непрерывных линейных операторов, действующих из X в Y, будем обозначать L(X, Y).
Системы линейных алгебраических уравнений, интегральные уравнения, а также различные задачи для обыкновенных дифференциальных уравнений и уравнений с производными часто могут быть записаны в виде линейного уравнения
Если существует обратный оператор 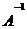
Важное значение приобретает теперь выявление условий, при выполнении которых обратный оператор существует и обладает теми или иными свойствами.
Пусть задан линейный оператор: А: X → Y, где X,Y – линейные пространства, причем его область определения D(A)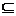
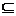
Введем множество 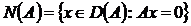
Теорема 4. Оператор А переводит D (А) в R (А) взаимно однозначно тогда и только тогда, когда N(A)=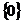
Теорема 5. Оператор А-1 существует и ограничен на R(A) тогда и только тогда, когда для некоторой постоянной m>0 и любого x Î D(A) выполняется неравенство
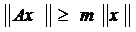
Введем теперь следующее важное понятие.
Будем говорить, что линейный оператор А: X → Y непрерывно обратим, если R(A)=Y , оператор обратим и A-1 Î L(Y, X), (т.е. ограничен).
Обращаясь к теореме 5, мы сможем сформулировать следующее утверждение.
Теорема 6. Оператор А непрерывно обратим тогда и только тогда, когда R(A)=Y и для некоторой постоянной m>0 и для всех 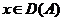
В случае определенного и ограниченного на всем множестве оператора A Î L(X,Y) имеется теорема Банаха об обратном операторе.
Теорема 7. Если А – ограниченный линейный оператор, отображающий взаимно однозначно банахово пространство X на банахово пространство Y, то обратный оператор А-1 ограничен.
Иными словами, если А Î L(X,Y), где X и Y банаховы, R(A)=Y и А обратим, то А непрерывно обратим.
Взглянем на понятие непрерывно обратимого оператора с точки зрения разрешимости линейного уравнения
Если А непрерывно обратим, то уравнение это имеет единственное решение x = A-1y для любой правой части у. Если при этом 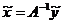

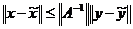
Пусть А Î L(X,Y). Оператор U Î L(X,Y) будем называть правым обратным к А, если AU = Iy. Оператор V Î L(X,Y) будем называть левым обратным к А, если VA = Ix.
Здесь через Iy (Ix) обозначен тождественный оператор в пространстве Y (X). Ниже для правого обратного к А используем обозначение Аr–1, а для левого – АL–1.
Лемма 1. Если существует правый обратный Аr–1 к А, то уравнение (2) имеет решение
Если существует левый обратный оператор к А, то уравнение (2) может иметь не более одного решения.
А(Аr–1 y) = (А Аr–1)y = y,
т.е. x = Аr–1 y обращает (2) в тождество и, значит, является решением.
Далее, пусть существует АL–1. рассмотрим N(A). Пусть x Î N(A), тогда Аx = 0. применим к этому равенству оператор АL–1, тогда АL–1Аx = 0, откуда x = 0. итак, всякое x Î N(A) оказывается равным 0. Значит, N(A) = <0>и, по теореме 4, А взаимно однозначен, т.е. для уравнения (2) справедлива теорема единственности. Что и требовалось доказать.
Пусть X – банахово пространство. Рассмотрим банахово пространство L(X) – пространство линейных, ограниченных и заданных на всем множестве операторов. Пусть I – тождественный оператор в L(X). Очевидно, что I непрерывно обратим. Ниже доказывается, что вместе с I непрерывно обратимы все операторы 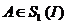
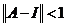
Для краткости положим C = I – A. Ниже мы будем ссылаться на признак Вейерштрасса: пусть X – банахово пространство, тогда всякий абсолютно сходящийся в X ряд сходится.
Теорема 8. Пусть 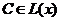
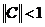
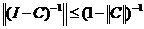
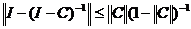
Доказательство. Рассмотрим в L(X) ряд
Так как 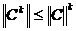
По признаку Вейерштрасса ряд (3) сходится равномерно, т.е.
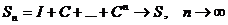
Где S – сумма ряда (3). Далее простой проверкой убеждаемся, что
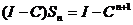
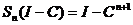
Но при этом 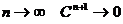
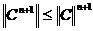
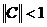
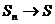
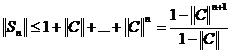
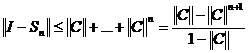
Переходя в этих неравенствах к пределу при 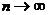
Теперь рассмотрим более общий случай пространства L(X,Y). Пусть А Î L(X,Y) непрерывно обратим.
Теорема 9. Пусть A, B Î L(X,Y), А непрерывно обратим и выполнено неравенство 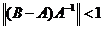
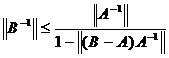
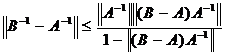
§4. Абстрактные функции
Пусть S – некоторое множество на числовой оси или в комплексной плоскости, а X – нормированное пространство.
Рассмотрим функцию x(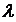
Пусть x(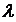
http://toehelp.ru/theory/toe/lecture27/lecture27.html
http://kazedu.com/referat/86674

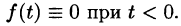
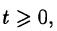 т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.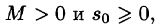 что для всех t выполняется неравенство
что для всех t выполняется неравенство 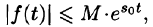 , т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число 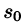 называется показателем роста f(t).
называется показателем роста f(t).