Определение и вывод уравнения пучка плоскостей

Пучок плоскостей

Доказательство необходимого условия. Дано: плоскость π₃ принадлежит пучку, образованному плоскостями π₁ и π₂, следовательно, π₁, π₂, π₃ принадлежат одному пучку плоскостей. Так как плоскости π₁ и π₂ различны, то ранг матрицы M≤2. Следовательно, левые части уравнения плоскостей π₁ и π₂ линейно независимы. Поэтому, левая часть в уравнении плоскости π₃ может быть представлена как линейная комбинация плоскостей π₁ и π₂, то есть существуют константы λ и μ, такие, что (1) A₃x+B₃y+C₃z+D₃=λ(A₁x+B₁y+C₁z+D₁)+μ(A₂x+B₂y+C₂z+D₂), где A₃=λA₁+μA₂, B₃=λB₁+μB₂, C₃=λC₁+μC₂, D₃=λD₁+μD₂.

Докажем достаточные условия теоремы 2. Дано: равенство 1, требуется доказать, что π₁, π₂, π₃ принадлежат одному пучку плоскостей. В самом деле, из равенства 1 следует, что A₃=λA₁+μA₂, B₃=λB₁+μB₂, C₃=λC₁+μC₂, D₃=λD₁+μD₂. Тогда третья строка матрицы M есть линейная комбинация первых двух строк этой матрицы. Следовательно, ранг матрицы M≤2, тогда, в силу теоремы 1, плоскость π₃ принадлежит пучку плоскостей, образованному π₁ и π₂. Следствие из теоремы 2: уравнение плоскости, проходящей через прямую пересечения двух плоскостей π₁ и π₂, заданных своими общими уравнениями относительно ПДСК, имеет вид A₁x+B₁y+C₁z+D₁+α(A₂x+B₂y+C₂z+D₂)=0, α=μ/λ≠0.

Чтобы добавить страницу в закладки, нажмите Ctrl+D.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Пучок плоскостей

Пучком плоскостей называют — множество всех плоскостей, проходящих через одну и ту же прямую KM (где KM — общая линия (прямая) пересечения плоскостей также называют её осью пучка см. рисунок ниже).

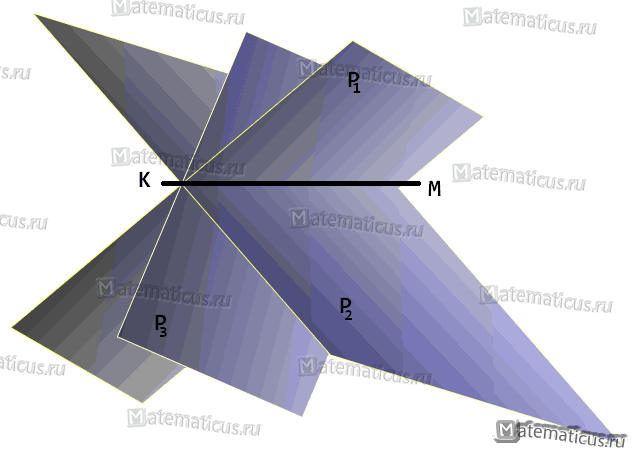
Если известны уравнения двух различных плоскостей P₁ и P₂

принадлежащих пучку, то каждую плоскость пучка можно представить уравнением вида:

Это уравнение называется уравнением пучка плоскостей
Когда m₁≠0, можно разделить уравнение на m₁. Обозначив m₁:m₂ через λ, получим уравнение:

Пример 1
Даны уравнения
5х-3у=0 и 3z-4x=0
Уравнение пучка есть:
m₁ ⋅ (5х-3у) + m₁ ⋅ (3z-4x )=0
Например, взяв m₁=1, m₂=-2, будем иметь:
1 ⋅ (5х-3у) + (-2) ⋅ (3z-4x )=0
Отсюда получаем:
13x-3y-6z=0
Уравнение представляет одну из плоскостей пучка.

Пример 2
Найти уравнения проекции прямой T
2x+3y+4z+5=0, x-6y+3z-7=0
на плоскость P
2x+2y+z+15=0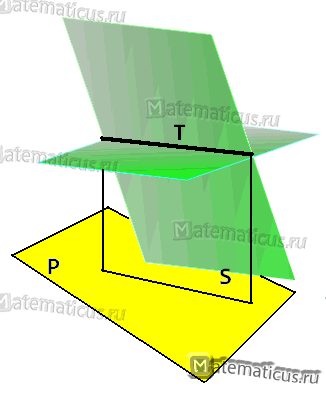

Решение

Искомая проекция представляется уравнением вида:
(2x+3y+4z+5)+λ ⋅ (x-6y+3z-7)=0

Чтобы найти λ, представим в виде:
(2+λ) ⋅ х+(3-6λ) ⋅ у+(4+3λ) ⋅ z+5-7λ=0 (1)
и запишем условие перпендикулярности плоскостей:

Подставляя A=2, B=2, C=1, получаем:
2 ⋅ (2+λ)+2 ⋅ (3-6λ)+1 ⋅ (4+3λ)=0
Отсюда λ=2. Подставляя λ=2 в уравнение (1), получим уравнение плоскости S. Искомая проекция представляется уравнениями:

Пучок прямых, уравнение пучка прямых

В статье рассматриваются определения пучка прямых с центром в заданной точке плоскости. Разбирается подробное решение с применением определения, рассматриваются задачи на составление уравнения пучка прямых, нахождение координат.

Пучок прямых – это определение

Пучок прямых определяется на плоскости, но не в трехмерном пространстве. Аксиома геометрии говорит о том, что если имеются две несовпадающие точки, расположенные на плоскости, то через них можно провести только одну прямую. Если на плоскости γ задается точка М 0 и M 1 , то через них можем провести прямую. Когда имеется еще одна точка М 2 , которая не лежит на прямой М 0 М 1 , тогда можно провести прямую М 0 М 2 . Если отметим точку М 3 , не принадлежащую ни одной из проведенных прямых, через нее также може провести прямую, проходящую через М 0 .

Отсюда следует, что в плоскости γ можно провести множество прямых через заданную точку. Это и привело к определению пучка прямых.

Заданная плоскость γ с множеством всех прямых, которые лежат в плоскости γ и проходящие через точку М 0 называют пучком прямых с центром в точке М 0 .

Исходя из определения, имеем, что любые две прямые из этого пучка пересекутся в центре данного пучка прямых. Пучок определяется при условии, если указан центр данного пучка.

Уравнение пучка прямых – решение задач

Для решения задач применяется уравнение пучка прямых, то есть сам пучок рассматривается относительно систему координат О х у на плоскости.

Когда имеем на плоскости прямоугольную систему координат О х у с указанными пересекающимися прямыми а 1 и а 2 _, пучок задает эти прямые. За систему координат О х у отвечает общее уравнение прямой, которое имеет вид A 1 x + B 1 y + C 1 = 0 или A 2 x + B 2 y + C 2 = 0 .

Введем обозначение пересечения прямых как точка М 0 с координатами х 0 и y 0 . Отсюда следует, что точка М имеет координаты M 0 ( x 0 , y 0 ) .

Чтобы определить вид используемого уравнения в пучках, рассмотрим на теореме.

При заданных двух пересекающихся прямых а 1 и а 2 имеются прямые, которые входят в пучок прямых, образованных в системе координат О х у . Их уравнения имеют вид A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 тогда и только тогда, когда уравнение прямой α · ( A 1 x + B 1 y + C 1 = 0 ) + β · ( A 2 x + B 2 y + C 2 ) = 0 соответствует ей,a α и β являются действительными числами, неравными нулю. Данное условие записывается так: α 2 + β 2 ≠ 0 .

Начнем рассмотрение доказательства с рассмотрения прямой a с указанного пучка, после чего докажем, что ее можно задавать при помощи уравнения α · ( A 1 x + B 1 y + C 1 ) + β · ( A 2 x + B 2 y + C 2 ) = 0 .

Центр пучка возьмем за точку с координатами M 0 = ( x 0 , y 0 ) .

Отсюда получаем, что n → = ( A 1 , B 1 ) является нормальным вектором прямой A 1 x + B 1 y + C 1 = 0 , тогда n 2 → = ( A 2 , B 2 ) — нормальный вектор для прямой A 2 x + B 2 y + C 2 = 0 . Получаем, что n → 1 и n 2 → — это неколлинеарные векторы, потому что у прямой а 1 и а 2 нет общих точек пересечения. Значит, необходимо разложить нормальный вектор n → по двум неколлинеарным n 1 → и n 2 → . Разложение необходимо выполнять по формуле n → = α · n 1 → + β · n 2 → . В итоге получаем, что n → = ( α · A 1 + β · A 2 , α · B 1 + β · B 2 ) .

После вычислений получаем координаты нормального вектора прямой a , равные n → = α · A 1 + β · A 2 , α · B 1 + β · B 2 . Координаты точки, пересекающиеся с прямой a в точке M 0 ( x 0 , y 0 ) , записываются при помощи общего уравнения прямой a . Тогда получаем выражение вида:

α · A 1 + β · A 2 · x — x 0 + α · B 1 + β · B 2 · y — y 0 = 0 ⇔ ⇔ α · ( A 1 x + B 1 y — A 1 x 0 + B 1 y 0 ) + β · A 2 x + B 2 y — A 2 x 0 — B 2 y 0 = 0

По — A 1 x 0 — B 1 y 0 = C 1 и — A 2 x 0 — B 2 y 0 = C 2 получим общее уравнение прямой a , имеющее вид α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 . Вышесказанная необходимость доказана.

Осталось найти доказательства достаточности.

Значит, нужно произвести доказательство выражения α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 , где имеем α и β некоторыми действительными числами неравными нулю, существует уравнение из пучка прямых с точкой пересечения M 0 ( x 0 , y 0 ) . Такое уравнение определено при помощи двух пересекающихся прямых A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Запишем уравнение α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 в виде α · A 1 + β · A 2 · x + α · B 1 + β · B 2 · y + α · C 1 + β · C 2 = 0 .

Уравнение будет считаться общим, если выполняется условие, когда α · A 1 + β · A 2 и α · B 1 + β · B 2 отличны от нуля. Иначе мы получили выражение вида α · A 1 + β · A 2 = 0 ⇔ A 1 = — β α · A 2 и α · B 1 + β · B 2 = 0 ⇔ B 1 = — β α · B 2 или α · A 1 + β · A 2 = 0 ⇔ A 2 = — α β · A 1 и α · B 1 + β · B 2 = 0 ⇔ B 2 = — α β · B 1 . Это значило бы, что векторы не коллинеарны.

Это невозможно в данном случае, так как n 1 → и n 2 → — это нормальные векторы прямых а 1 и а 2 , которые пересекаются.

Имеем, что уравнение α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 является общим уравнением прямой. Далее необходимо произвести доказательство удовлетворения координат точки при их пересечении, то есть координаты точки M 0 ( x 0 , y 0 ) . Докажем, справедливо ли равенство α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 .

M 0 ( x 0 , y 0 ) является точкой пересечения прямых, значит, ее координаты должны удовлетворять уравнениям обеих пересекающихся прямых.

Когда A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 справедливы, отсюда следует, что α · A 1 x + B 1 y + C 1 + β · A 2 x + B 2 y + C 2 = α · 0 + β · 0 = 0 .

Что и требовалось доказать.

Можем сделать вывод, что уравнение, которое имеет вид α · A 1 x + B 1 y + C 1 + β · A 2 x + B 2 y + C 2 = 0 и есть уравнение пучка.

Значения α и β необходимы для того, чтобы определять прямые, находящиеся в данном пучке, с уравнениями A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Необходимо, чтобы как минимум один из параметров был не равен нулю, тогда можно упростить выражение. При условии, что α ≠ 0 получаем выражение вида A 1 x + B 1 y + C 1 + λ · A 2 x + B 2 y + C 2 = 0 с λ = α β .

При β ≠ 0 выражение принимает вид μ · A 1 x + B 1 y + C 1 + A 2 x + B 2 y + C 2 = 0 с μ = α β .

Они не являются эквивалентными уравнению пучка прямых, относящихся к виду α · A 1 x + B 1 y + C 1 + β · A 2 x + B 2 y + C 2 = 0 . Уравнение A 1 x + B 1 y + C 1 + λ · A 2 x + B 2 y + C 2 = 0 при любых значениях λ не даст возможности получить уравнение вида A 2 x + B 2 y + C 2 = 0 .

Уравнение μ · A 1 x + B 1 y + C 1 + A 2 x + B 2 y + C 2 = 0 при любых значениях μ не даст в результате A 1 x + B 1 y + C 1 = 0 .

Подробно рассмотрим на решении примеров.

Написать уравнение прямой пучка с заданным центром в точке M 0 ( — 1 , 4 ) , k = 3 .

Необходимо составить уравнение прямой, которая будет проходить через заданную точку с координатами M 0 ( — 1 , 4 ) с угловым коэффициентом равным 3 . Тогда запишем уравнение прямой с угловым коэффициентом и получим y — 4 = 3 · ( x — ( — 1 ) ) ⇔ y = 3 x + 7 .

Ответ: y = 3 x + 7 .

Найти координаты центра пучка прямых в О х у , если известны два уравнения пересекающихся прямых x — 4 2 = y + 3 0 и x 2 3 + y — 1 = 1 .

Чтобы найти координаты центра пучка, необходимо найти точки пересечения x — 4 2 = y + 3 0 и x 2 3 + y — 1 = 1 .

Получим, что каноническое уравнение прямой на плоскости x — 4 2 = y + 3 0 эквивалентно x 2 3 + y — 1 = 1 , а уравнение в отрезках x 2 3 + y — 1 = 1 общему уравнению прямой 3 2 x — y — 1 = 0 .

Теперь составляем систему уравнений, включающую в себя уравнения прямых.

y + 3 = 0 3 2 x — y — 1 = 0 ⇔ y = — 3 3 2 x — ( — 3 ) — 1 = 0 ⇔ y = — 3 x = — 4 3

Получим, что — 4 3 , — 3 — это координаты центральной точки, где пересекаются все прямые.

Произвести составление уравнения пучка прямых в О х у , которое задано при помощи прямых 3 x — 2 y + 1 = 0 и x = — 2 + 2 · λ y = 5 · λ , имеющих общую точку пересечения.

Для начала необходимо получить общее уравнение прямой. Оно определено параметрическим уравнением x = — 2 + 2 · λ y = 5 · λ .

Отсюда следует, что

x = — 2 + 2 · λ y = 5 · λ ⇔ λ = x + 2 2 λ = y 5 ⇔ x + 2 2 = y 5 ⇔ ⇔ 5 · ( x + 2 ) = 2 · y ⇔ 5 x — 2 y + 10 = 0

Произведем запись уравнения пучка прямых и получим α · ( 3 x — 2 y + 1 ) + β · ( 5 x — 2 y + 10 ) = 0 , а α и β являются действительными числами, где обязательным условием считается α 2 + β 2 ≠ 0 .

Ответ: α · ( 3 x — 2 y + 1 ) + β · ( 5 x — 2 y + 10 ) = 0 .

Написать уравнение прямой, проходящей через точку M 1 ( 2 , — 1 ) и принадлежащей пучку прямых с уравнением α · ( 5 x + y — 19 ) + β · ( 2 x — 3 y + 6 ) = 0 .

Задача решается двумя способами.

Первый способ начинается с определения М 0 , являющейся центром пересечения. Тогда нужно найти точки пересечения уравнений 5 x + y — 19 = 0 и 2 x — 3 y + 6 = 0 , а их результат и будет являться координатами для M 0 .

Определяем координаты, решив получившуюся систему:

5 x + y — 19 = 0 2 x — 3 y + 6 = 0 ⇔ y = 19 — 5 x 2 x — 3 · ( 19 — 5 x ) + 6 = 0 ⇔ y = 19 — 5 x x = 3 ⇔ ⇔ y = 19 — 5 · 3 x = 3 ⇔ y = 4 x = 3

Значит точка М 0 имеет координаты ( 3 , 4 ) . Это записывается как M 0 ( 3 , 4 ) . Чтобы получить искомое уравнение , которое проходит через точки с координатами M 0 ( 3 , 4 ) и M 1 ( 2 , — 1 ) . В итоге получаем:

x — 3 2 — 3 = y — 4 — 1 — 4 ⇔ x — 3 — 1 = y — 4 — 5 ⇔ x — 3 1 = y — 4 5

Второй способ начинается с того, что необходимо определить параметры α и β , чтобы уравнение α · ( 5 x + y — 19 ) + β · 2 x — 3 y + 6 = 0 было уравнением прямой, которая проходит через M 1 ( 2 , — 1 ) . Для этого найдем координаты М 1 и получим, что

α · 5 · 2 + ( — 1 ) — 19 + β · 2 · 2 — 3 · ( — 1 ) + 6 = 0 ⇔ ⇔ — 10 · α + 13 · β = 0 ⇔ α = 13 · β 10

Принимаем значение β = 10 , при желании можно выбирать любое другое такое значение β , которое дает несложное вычисление α . Получаем α = 13 · β 10 = 13 · 10 10 = 13 .

При подстановке значений α = 13 и β = 10 в заданное уравнение пучка, преобразуем:

13 · ( 5 x + y — 19 ) + 10 · ( 2 x — 3 y + 6 ) = 0 ⇔ 85 x — 17 y — 187 = 0 ⇔ 5 x — y — 11 = 0

Необходимо проверить эквивалентность получившихся уравнений.

x — 3 1 = y — 4 5 ⇔ 5 · x — 3 = 1 · y — 4 ⇔ 5 x — y — 11 = 0

Отсюда следует, что все решено верно.

Ответ: 5 x — y — 11 = 0 .

Определить принадлежность прямой 3 x — y + 5 = 0 пучку прямых α · ( x — 2 y + 4 ) + β · ( x — y + 4 ) = 0 .

Решение производится двумя способами.

Первый способ решения начинается с нахождения центров координаты заданного уравнения пучка и их проверки:

x — 2 y + 4 = 0 x — y + 4 = 0 ⇔ x = 2 y — 4 x — y + 4 = 0 ⇔ x = 2 y — 4 2 y — 4 — y + 4 = 0 ⇔ ⇔ x = 2 y — 4 y = 0 ⇔ x = 2 · 0 — 4 y = 0 ⇔ x = — 4 y = 0 3 · ( — 4 ) — 0 + 5 = 0 ⇔ — 7 = 0

Получим, что подстановка координат центра в уравнение прямой 3 x — y + 5 = 0 дает неверное равенство. Делаем вывод, что прямая не пересекает центр пучков, значит, и не принадлежит ему.

Второй способ начинается с раскрытия скобок и приведения подобных слагаемых α · ( x — 2 y + 4 ) + β · x — y + 4 = 0 ⇔ 2 α + β · y + 4 α + 4 β = 0 .

Когда прямая 3 x — y + 5 = 0 принадлежит пучку прямых, тогда имеются такие значения α и β , что два уравнения α + β · x — 2 α + β · y + 4 α + 4 β = 0 и 3 x — y + 5 = 0 являются эквивалентными.

Тогда получаем систему, состоящую из трех равнений α + β = 3 2 α + β = 1 4 α + 4 β = 5 .

Для ее преобразования необходимо приравнять коэффициенты перед переменными x и y и свободные членов имеющихся уравнений α + β · x — 2 α + β · y + 4 α + 4 β = 0 и 3 x — y + 5 = 0 , чтобы получать результат решения.

Для проверки необходимо применить теорему Кронекера-Капелли.

Для этого необходимо записать основную и расширенную матрицы для составленной системы уравнений. Получим, что A = 1 1 2 1 4 4 и T = 1 1 3 2 1 1 4 4 5 .

Требуется посчитать ранг матрицы A . Он равен 2 , потому что 1 1 2 1 = — 1 ≠ 0 .

Результат нахождения ранга расширенной матрицы равняется 3 , потому как 1 1 3 2 1 1 4 4 5 = 7 ≠ 0 .

Отсюда имеем, что система уравнений α + β = 3 2 α + β = 1 4 α + 4 β = 5 не определена, то есть имеет решений. Так как решения отсутствуют, прямая не проходит через центр прямой имеющихся пучков прямых.

Ответ: нет, прямая 3 x — y + 5 = 0 не принадлежит заданному пучку прямых, записанных уравнением вида α · ( x — 2 y + 4 ) + β · ( x — y + 4 ) = 0 .