Алгебра
План урока:
Иррациональные уравнения
Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.
Приведем примеры иррациональных ур-ний:
Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.
Простейшие иррациональные уравнения
Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:
где а – некоторое число (константа), f(x) – рациональное выражение.
Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:
Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии
n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.
Ответ: корней нет.
Пример. Решите ур-ние
Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:
Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).
Пример. Найдите решение ур-ния
Решение. Возведем обе части в пятую степень:
х 2 – 14х – 32 = 0
Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:
D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324
Итак, нашли два корня: (– 2) и 16.
Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.
Пример. Решите ур-ние
Решение. Возводим обе части во вторую степень:
х – 2 = х 2 – 8х + 16
D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9
Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):
при х = 3 х – 4 = 3 – 4 = – 1
при х = 6 6 – 4 = 6 – 4 = 2
Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.
Пример. Решите ур-ние
Решение. Здесь используется кубический корень, а потому возведем обе части в куб:
3х 2 + 6х – 25 = (1 – х) 3
3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3
Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:
Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.
Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:
при х = 2 1 – х = 1 – 2 = – 1
Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:
Уравнения с двумя квадратными корнями
Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.
Пример. Решите ур-ние
Решение. Перенесем вправо один из корней:
Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:
Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:
Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:
(2х – 4) 2 = 13 – 3х
4х 2 – 16х + 16 = 13 – 3х
4х 2 – 13х + 3 = 0
D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121
Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:
Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3
На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.
Введение новых переменных
Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние
Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.
Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:
х 1/2 – 10х 1/4 + 9 = 0
Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид
Это квадратное ур-ние. Найдем его корни:
D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64
Получили два значения t. Произведем обратную замену:
х 1/4 = 1 или х 1/4 = 9
Возведем оба ур-ния в четвертую степень:
(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4
х = 1 или х = 6561
Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:
В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.
Пример. Решите ур-ние
х 1/3 + 5х 1/6 – 24 = 0
Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:
Его корни вычислим через дискриминант:
D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121
Далее проводим обратную заменуx 1/6 = t:
х 1/6 = – 8 или х 1/6 = 3
Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.
Замена иррационального уравнения системой
Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите ур-ние
Решение. Заменим первый корень буквой u, а второй – буквой v:
Исходное ур-ние примет вид
Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:
Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:
Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:
(х + 6) + (11 – х) = u 3 + v 2
из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:
17 = u 3 + (5 – u) 2
17 = u 3 + u 2 – 10u + 25
u 3 + u 2 – 10u + 8 = 0
Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа
подставим полученные значения в (4):
x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3
x + 6 = 1 или х + 6 = 8 или х + 6 = – 64
х = – 5 или х = 2 или х = – 70
Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим
Корень подошел. Проверяем следующее число, х = 2:
Корень снова оказался верным. Осталась последняя проверка, для х = – 70:
Итак, все три числа прошли проверку.
Уравнения с «вложенными» радикалами
Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:
При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:
Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:
Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:
Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:
Возводим в квадрат и получаем:
х 2 + 40 = (х + 4) 2
х 2 + 40 = х 2 + 8х + 16
И снова нелишней будет проверка полученного корня:
Иррациональные неравенства
По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:
Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.
Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида
Может быть справедливым только тогда, когда
То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во
при четном n можно заменить системой нер-в
Пример. При каких значениях x справедливо нер-во
Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:
х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)
Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во
чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.
Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.
Пример. Найдите решение нер-ва
Решение. Всё очень просто – надо всего лишь возвести обе части в куб:
x 2 – 7x– 8 2 – 7x– 8 = 0
D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81
Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:
Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.
Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.
Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид
Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.
Пример. Решите нер-во
Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):
И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:
D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9
Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.
стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:
f(x) > 0 (подкоренное выражение не может быть отрицательным);
g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).
Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.
Пример. Решите нер-во
Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим
х 2 – 10х + 21 > 0(1)
Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:
Во-вторых, выражение 4 – х не может быть отрицательным:
Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):
Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:
Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:
Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:
Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:
Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).
Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3
Иррациональные уравнения. Решение иррациональных уравнений.
Иррациональные уравнения – это один из видов уравнений, изучаемых на уроках математики в школе. Сейчас мы познакомимся с иррациональными уравнениями: узнаем определение иррациональных уравнений, рассмотрим примеры, взглянем на простейшие иррациональные уравнения. После этого переключимся на решение иррациональных уравнений: запишем универсальный алгоритм, изучим все методы решения иррациональных уравнений и детально разберем примеры решения иррациональных уравнений.
Иррациональные уравнения
Иррациональные уравнения – это… Определение
Иррациональные уравнения – это уравнения, в которых переменная содержится под знаком корня.
Приведенное определение объективно является самым простым, понятным и удобным определением иррационального уравнения. Оно позволяет по одному взгляду на уравнение определить, является оно иррациональным уравнением или нет: для этого нужно лишь посмотреть, есть переменная под знаком корня или нет.
Необходимо заметить, что в некоторых учебниках алгебры и начал анализа иррациональные уравнения определяются немного иначе. В одних книгах уточняется вид выражений, которые могут находиться под знаками корней, в других – к иррациональным уравнениям причисляют уравнения с переменной, находящейся в основании степени с дробным рациональным показателем. Эти нюансы раскрыты в материале что такое иррациональные уравнения. Там же упомянуто про иррациональные уравнения с несколькими переменными и про иррациональные уравнения с параметром.
Примеры иррациональных уравнений
Запишем несколько иррациональных уравнений, отвечающих определению из предыдущего пункта:
Во всех записанных уравнениях есть переменная под знаком корня, значит, это иррациональные уравнения.
Простейшие иррациональные уравнения
В некоторых задачниках можно встретить словосочетание «простейшие иррациональные уравнения». Обычно под простейшими иррациональными уравнениями понимают иррациональные уравнения, которые можно описать формулой 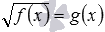
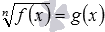
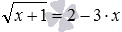
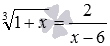
Решение иррациональных уравнений
Алгоритм решения иррациональных уравнений
Решение иррациональных уравнений проводится в соответствии с универсальным алгоритмом решения иррациональных уравнений. Чтобы решить иррациональное уравнение, надо:
- Выбрать подходящий метод решения
- Провести решение.
Методы решения иррациональных уравнений
Решение иррациональных уравнений упирается в
- знание методов решения иррациональных уравнений,
- умение выбирать подходящий метод в каждом конкретном случае
- и в умение проводить решение иррационального уравнения выбранным методом.
Сейчас мы перечислим и разберем все основные методы решения иррациональных уравнений, после этого дадим рекомендации по выбору метода.
Из представленной таблицы видно, что для решения иррациональных уравнений используются практически все известные методы решения уравнений. Давайте уделим внимание каждому из них:
- Метод решения иррациональных уравнений по определению корня наиболее удобно использовать при решении иррациональных уравнений
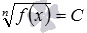 , в левых частях которых находятся корни, а в правых – числа. В частности, метод позволяет констатировать отсутствие решений в случае четного показателя корня и отрицательного числа в правой части. Например, иррациональное уравнение
, в левых частях которых находятся корни, а в правых – числа. В частности, метод позволяет констатировать отсутствие решений в случае четного показателя корня и отрицательного числа в правой части. Например, иррациональное уравнение 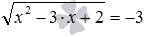 с квадратным корнем в левой части и отрицательным числом в правой части не имеет решений. В случае неотрицательного числа в правой части или нечетного показателя корня иррациональное уравнение
с квадратным корнем в левой части и отрицательным числом в правой части не имеет решений. В случае неотрицательного числа в правой части или нечетного показателя корня иррациональное уравнение 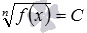 по определению корня заменяется решением уравнения C n =f(x) . Так решение иррационального уравнения
по определению корня заменяется решением уравнения C n =f(x) . Так решение иррационального уравнения 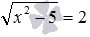 заменяется решением уравнения 2 2 =x 2 −5 , а от иррационального уравнения
заменяется решением уравнения 2 2 =x 2 −5 , а от иррационального уравнения 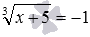 можно перейти к уравнению (−1) 3 =x+5 .
можно перейти к уравнению (−1) 3 =x+5 .Метод решения иррациональных уравнений по определению корня применяется и для решения иррациональных уравнений 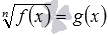
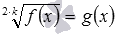
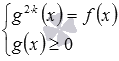
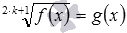

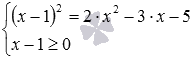
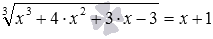
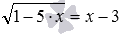 по методу возведения обеих частей уравнения в квадрат сводится к уравнению 1−5·x=(x−3) 2 , не содержащему знаков корней в записи. Метод возведения обеих частей уравнения в одну и ту же степень позволяет решать и многие другие иррациональные уравнения более сложного вида с двумя, тремя и большим количеством корней в записи, с корнями под корнями и т.д. Например, методом возведения обеих частей уравнения в одну и ту же степень могут быть решены следующие иррациональные уравнения:
по методу возведения обеих частей уравнения в квадрат сводится к уравнению 1−5·x=(x−3) 2 , не содержащему знаков корней в записи. Метод возведения обеих частей уравнения в одну и ту же степень позволяет решать и многие другие иррациональные уравнения более сложного вида с двумя, тремя и большим количеством корней в записи, с корнями под корнями и т.д. Например, методом возведения обеих частей уравнения в одну и ту же степень могут быть решены следующие иррациональные уравнения: 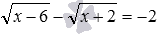 ,
, 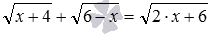 ,
, 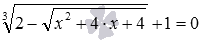 и т.п. При этом к возведению частей уравнения в степень приходится прибегать несколько раз и пользоваться дополнительным техническим приемом, называемым уединение радикала. Наконец, необходимо помнить, что при решении иррациональных уравнений методом возведения обеих частей в четную степень (в квадрат, четвертую, шестую и так далее) необходимо проводить отсеивание посторонних корней.
и т.п. При этом к возведению частей уравнения в степень приходится прибегать несколько раз и пользоваться дополнительным техническим приемом, называемым уединение радикала. Наконец, необходимо помнить, что при решении иррациональных уравнений методом возведения обеих частей в четную степень (в квадрат, четвертую, шестую и так далее) необходимо проводить отсеивание посторонних корней.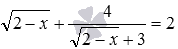 переменная находится только в составе корней
переменная находится только в составе корней 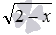 , значит, для решения целесообразно использовать метод введения новой переменной. Обязательно стоит изучить возможность введения новой переменной в случаях, когда в иррациональных уравнениях фигурируют корни с одинаковыми подкоренными выражениями, но разными показателями корня, корни из взаимно обратных выражений. Для наглядности приведем несколько характерных иррациональных уравнений:
, значит, для решения целесообразно использовать метод введения новой переменной. Обязательно стоит изучить возможность введения новой переменной в случаях, когда в иррациональных уравнениях фигурируют корни с одинаковыми подкоренными выражениями, но разными показателями корня, корни из взаимно обратных выражений. Для наглядности приведем несколько характерных иррациональных уравнений: 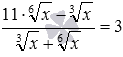 ,
, 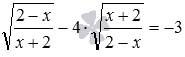 .
.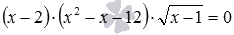 . Это иррациональное уравнение по методу разложение на множители на области допустимых значений переменной x для этого уравнения заменяется совокупностью трех уравнений x−2=0 , x 2 −x−12=0 и
. Это иррациональное уравнение по методу разложение на множители на области допустимых значений переменной x для этого уравнения заменяется совокупностью трех уравнений x−2=0 , x 2 −x−12=0 и 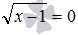 .
.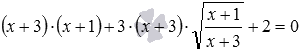 . Также очень широко используются и другие преобразования, хорошо известные к моменту изучения иррациональных уравнений, такие как перенос слагаемых из одной части уравнения в другую с изменением их знаков на противоположные, умножение и деление обеих частей уравнения на отличное от нуля число и др. Например, вынесение за скобки общего множителя
. Также очень широко используются и другие преобразования, хорошо известные к моменту изучения иррациональных уравнений, такие как перенос слагаемых из одной части уравнения в другую с изменением их знаков на противоположные, умножение и деление обеих частей уравнения на отличное от нуля число и др. Например, вынесение за скобки общего множителя  в уравнении
в уравнении 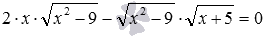 позволяет проводить дальнейшее решение методом разложения на множители.
позволяет проводить дальнейшее решение методом разложения на множители.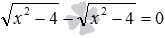 и
и 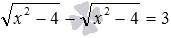 . Первое из них сводится к верному числовому равенству 0=0 , его решением является любое число из ОДЗ. А второе иррациональное уравнение сводится к неверному числовому равенству 0=3 , оно решений не имеет.
. Первое из них сводится к верному числовому равенству 0=0 , его решением является любое число из ОДЗ. А второе иррациональное уравнение сводится к неверному числовому равенству 0=3 , оно решений не имеет.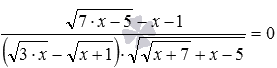 . По этому методу на ОДЗ для исходного уравнения нужно решить уравнение, являющееся результатом приравнивания числителя дроби к нулю.
. По этому методу на ОДЗ для исходного уравнения нужно решить уравнение, являющееся результатом приравнивания числителя дроби к нулю.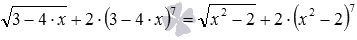 .
.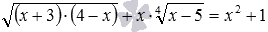 ОДЗ есть пустое множество, это позволяет констатировать, что уравнение не имеет решений.
ОДЗ есть пустое множество, это позволяет констатировать, что уравнение не имеет решений.- Графический метод решения уравнений может выручить, когда функции, отвечающие частям иррационального уравнения, довольно простые в плане построения графиков. В частности, графически могут быть решены иррациональные уравнения
и
.
- Решение иррациональных уравнений проводится методом решения уравнений через возрастание-убывание, когда очевиден или легко подбирается корень иррационального уравнения, а также просматривается возможность обосновать возрастание одной из функций, отвечающих частям уравнения, и убывание другой функции. Например, несложно подобрать корень иррационального уравнения
, также несложно обосновать убывание функции в левой части уравнения и возрастание функции в правой части уравнения.
- Иногда решить иррациональное уравнение позволяет метод оценки. Это касается тех случаев, когда не видно альтернативных более простых методов решения иррациональных уравнений, а также есть возможность получить подходящие оценки значений частей уравнения. В качестве примера приведем иррациональное уравнение
. Оценки его частей
и
позволяют получить решение.
Итак, мы рассмотрели все основные методы решения иррациональных уравнений. Хорошее владение ими позволяет довольно быстро выбрать подходящий метод решения для каждого конкретного иррационального уравнения. Также в этом помогают следующие рекомендации по выбору метода решения иррационального уравнения.
Примеры решения иррациональных уравнений
В этом пункте собраны примеры решения иррациональных уравнений. На них мы разберем все основные тонкости, возникающие при решении иррациональных уравнений. Для удобства разобьем примеры по группам в соответствии с применяемыми методами решения.
Первыми рассмотрим примеры решения иррациональных уравнений по определению корня. Три следующих примера демонстрируют, как определение корня позволяет решать иррациональные уравнения с корнем в левой части и числом в правой части:
Иррациональные уравнения. Методы решения.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Иррациональными уравнениями называются уравнения, содержащие переменную под знаком радикала (корня) или под знаком возведения в дробную степень. При этом, степень корня может быть произвольной.
Из определения следует, что если в записи уравнения нет знака корня (или дробного показателя степени), то уравнение не является иррациональным. Однако, не все уравнения, содержащие знаки корней, являются иррациональными. Действительно, в иррациональном уравнении под знаком корня должна быть переменная, и если её там нет, то уравнение не является иррациональным.
Например, В этих уравнениях под знаком корня стоят числа, а не переменные, значит, они не являются иррациональными.
Перечислим основные методы решения иррациональных уравнений.
По определению корня.
Метод возведения обеих частей уравнения в одну и ту же степень.
Метод введения новой переменной.
Метод разложения на множители.
Решение иррациональных уравнений через ОДЗ.
Решение иррациональных уравнений вида «дробь равна нулю».
Приведение иррациональных уравнений к числовым равенствам.
Преобразование иррациональных уравнений.
Рассмотрим каждый из перечисленных методов.
С помощью определения корня обычно решаются простейшие иррациональные уравнения, т.е. уравнения вида , где и – некоторые рациональные выражения. Решение таких уравнений зависит от чётности показателя корня.
Рассмотрим сначала случай, когда в правой части содержится число, т.е.
Если п – чётное, т.е. , где , то
Если п – нечётное, т.е. , где , то
Теперь рассмотрим случай, когда в правой части стоит выражение, зависящее от х, т.е.
Если п – чётное, т.е. , где , то
Если п – нечётное, т.е. , где , то
В основе метода возведения обеих частей уравнения в одну и ту же степень лежит следующее утверждение:
Возведение обеих частей уравнения в одну и ту же чётную натуральную степень даёт уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечётную степень даёт равносильное уравнение.
Поэтому, при возведении в чётную степень, необходимо находить область допустимых значений, либо выполнять проверку для найденных корней.
Этот метод обычно используется при решении уравнений вида
Если п – чётное, т.е. , где , то
Для упрощения записи решения уравнения, неравенства можно вынести в ОДЗ. Это будет выглядеть так:
Если п – нечётное, т.е. , где , то
ОДЗ, значит, этот корень посторонний.
Оба корня принадлежат области допустимых значений, значит, они являются корнями исходного уравнения.
уравнение не имеет действительных корней.
принадлежит области допустимых значений, значит, этот корень является корнем исходного уравнения.
Теперь к области допустимых значений добавляется ещё одно условие:
не принадлежат области допустимых значений, значит, этот корень посторонний.
Удобным методом решения иррациональных уравнений является метод введения новой переменной . Метод, обычно, применяется в случае, если в уравнении неоднократно встречается некоторое выражение с переменной. Тогда имеет смысл обозначить это выражение другой переменной.
Более сложным является случай, когда в уравнении присутствуют корни разных степеней. В этом случае есть смысл обозначить каждый корень другой переменной. Это можно выразить формулой:
Так как в уравнении присутствует корень нечётной степени, то находить ОДЗ не имеет смысла.
Введём новую переменную: , тогда . Значит, исходное уравнение принимает вид:
Возвращаемся к исходной переменной:
Введём новые переменные:
Тогда исходное уравнение равносильно системе:
Решим кубическое уравнение методом разложения на множители:
Возвращаемся к исходной переменной. Для этого достаточно использовать только одну из двух замен.
Метод разложения на множители используется тогда, когда достаточно просто найти общие множители в записи уравнения. Общий множитель выносится за скобки и используется свойство равенства нулю произведения.
Вынесем за скобки
Оба корня принадлежат области допустимых значений.
Функционально-графический метод используется в тех иррациональных уравнениях, когда остальные методы бессильны.
Можно выделить три основных направления функционально-графического метода решения иррациональных уравнений:
использование графиков функций (графический метод);
использование свойств возрастающих и убывающих функций (использование монотонности функций);
использование свойств ограниченных функций (метод оценки).
Эти три направления помогают решить подавляющее большинство иррациональных уравнений.
Обычно, этим методом решаются те уравнения, которые невозможно решить другим методом и графики функций, входящих в состав уравнения являются элементарными или получаются из таковых геометрическим преобразованием (растяжение, сжатие, смещение, сложение и вычитание).
Алгоритм использования графического метода:
построить графики функций, входящих в уравнение;
по взаимному расположению графиков сделать вывод о наличии и количестве корней решаемого уравнения:
если графики функций не пересекаются, то уравнение корней не имеет;
если графики функций имеют общие точки, то корнями уравнения являются абсциссы этих точек.
Следует учитывать, что, используя графический метод, сложно достичь высокой точности нахождения корней, поэтому, все найденные корни уравнения будут лишь приближёнными, нуждающимися в проверке и обосновании.
Для наглядности приведём простой пример.
На одной системе координат строим графики функций и .
Графики этих функций пересекаются в одной точке, значит, уравнение имеет один корень. Точка пересечения имеет координаты , значит, . Произведя проверку, убеждаемся, что этот корень точный.
Равенство верное, значит, .
Использование свойств возрастающих и убывающих функций.
Часто вместо графиков удобнее использовать свойства монотонности функций (свойства возрастания и убывания). Это происходит чаще всего в тех случаях, когда нужно найти количество корней уравнения.
Этот метод основывается на утверждении, которое следует из определения возрастания и убывания функции.
Если на множестве Х функции и непрерывны и одна из них возрастает, а другая убывает, то уравнение либо имеет единственный корень, либо не имеет корней.
Это утверждение верно как для иррациональных уравнений, так и для любых других.
Что касается нахождения значения корня уравнения, то, обычно, он является числом из ОДЗ и легко угадывается. Проверкой определяется правильность выбора корня.
Найдём область допустимых значений уравнения:
Функции и непрерывны на всей области допустимых значений.
Исследуем на монотонность функции и для .
Функция – линейная, угловой коэффициент у неё отрицательный, значит, она убывающая на всей области определения. Корень из убывающей функции – есть функция убывающая, значит, – убывающая для . Функция – обратная пропорциональность, она убывающая для всех , т.к. коэффициент . Значит, функция , равная сумме убывающих функций является убывающей на отрезке .
Функция – кубическая, она возрастающая на всей области определения, т.к. коэффициент положительный; функция также возрастающая при .
Итак, при функции, записанные в левой и правой частях уравнения являются непрерывными, причём одна из них убывает, а другая возрастает. Значит, уравнение либо не имеет корней, либо имеет единственный корень. Попробуем его отыскать. Методом подбора предполагаем, что и выполним проверку:
Равенство получилось верное, значит, уравнение имеет единственный корень .
Этот метод использует ограниченность функций.
Алгоритм метода оценки.
оцениваем значения функций в обеих частях уравнения;
ищем корни уравнения, используя полученные оценки, или обосновываем их отсутствие.
Способов оценки значений функции существует несколько. Мы рассмотрим все способы, поскольку в иррациональных уравнениях могут использоваться не только выражения с корнем.
оценка на основании определения корня с чётным показателем;
оценка на основании свойства корней: если , то ;
оценка на основании свойства степени с чётным показателем:
оценка значений квадратного трёхчлена;
оценка на основании свойств числовых неравенств;
оценка с использованием наибольшего и наименьшего значений функции.
Рассмотрим их подробнее.
Т.к., по определению, корень с чётным показателем есть неотрицательное число, то для любого х из области допустимых значений справедливо неравенство , где – некоторое выражение. Причём, понятно, что только тогда, когда .
Если выполняется неравенство , где , то для любого х из области допустимых значений справедливо неравенство .
Так как любое число в чётной степени есть неотрицательное число, то это свойство распространяется и на многочлены, т.е. для любого х из области допустимых значений справедливо неравенство . Также понятно, что тогда и только тогда, когда .
Если выражение задано в виде квадратного трёхчлена, то для его оценки необходимо сначала проверить на знак дискриминант.
Если , то значение квадратного трёхчлена оцениваем с помощью ординаты вершины параболы. Напомним, что . Тогда , если (ветви параболы направлены вверх); и , если (ветви параболы направлены вниз).
Если , то значение квадратного трёхчлена сравниваем с нулём: если , то , если , то .
Оценка на основе свойств числовых неравенств. Вспомним эти свойства.
Если к обеим частям верного неравенства прибавить (или отнять) некоторое число, то получится равносильное неравенство.
, где a и с – некоторые числа.
Если обе части верного неравенства умножить (или разделить) на одно и то же положительное число, то получится равносильное неравенство.
, где а и с – некоторые числа, причём .
Если обе части верного неравенства умножить (или разделить) на одно и то же отрицательное число и поменять знак неравенства на противоположный, то получится равносильное неравенство.
, где а и с – некоторые числа, причём .
Если в верном неравенстве обе положительные части заменить обратными выражениями и поменять знак неравенства на противоположный, то получится равносильное неравенство на всей области допустимых значений.
Если верные неравенства почленно сложить, то получится верное неравенство.
Если , где — некоторые числа, то справедливо неравенство:
Если верные неравенства с положительными левой и правой частями почленно умножить, то получится верное неравенство.
Если , где – положительные выражения, и — положительные числа, то справедливы неравенства:
Если , причём , то .
Оценка с использованием наибольшего и наименьшего значения функции.
Если наименьшее значение функции равно , то , на всей области определения.
Если наибольшее значение функции равно , то , на всей области определения.
После оценки значений функции, нужно сделать заключение о существовании решений уравнения.
Уравнение не имеет решений на множестве допустимых значений, если:
Уравнение равносильно системе уравнений на множестве допустимых значений, если:
, где и , причём – неотрицательные числа.
Уравнение не имеет решений на множестве допустимых значений, если:
Уравнение равносильно системе уравнений для любого х из области допустимых значений, если (или наоборот).
Произведём оценку левой и правой части уравнения.
Т.к. при любом значении х, то при любом х, а это значит, что . Поэтому,
Т.к. , то , а значит, . Поэтому, .
Мы получили, что , а . Значит, исходное уравнение равносильно системе двух уравнений:
Из второго уравнения легко найден единственный корень . Подставив его в первое уравнение, мы получили неверное равенство. Это означает, что система уравнений, а, значит, и исходное уравнение решений не имеет.
Ответ: решений нет.
Зададим функцию . Она состоит из суммы трёх слагаемых, значит, , где . Произведём оценку каждой из этих функций.
Т.к. , то , значит, . Поэтому,
Т.к. , то , значит, . Поэтому,
Т.к. , то , значит, . Поэтому,
Зная, что , , и , заключаем, что , т.е. . А т.к. , то исходное уравнение решений не имеет.
Ответ: решений нет.
Рассмотрим похожий пример: .
Рассуждения такие же, как и в предыдущем примере.
Т.к. , то , значит, . Поэтому,
Т.к. , то , значит, . Поэтому,
Значит, . Используя пункт 2 из метода оценки, переходим к системе:
Метод использования области допустимых значений (ОДЗ) является частью решения иррациональных уравнений, поскольку, практически всегда в таких уравнениях находим ОДЗ.
Если областью допустимых значений уравнения является пустое множество, значит, уравнение корней не имеет.
Если область допустимых значений имеет конечное множество чисел, то, подставляя каждое из них в исходное уравнение, находим корни.
Если область допустимых значений имеет бесконечное множество чисел, то рассматриваем другой способ решения.
Найдём область допустимых значений.
Область допустимых значений состоит из пустого множества, значит, исходное уравнение корней не имеет.
Ответ: корней нет.
Найдём область допустимых значений.
Так как область допустимых значений состоит из двух чисел и , то проверим, обращает ли каждое из них исходное уравнение в верное равенство.
Значит, является корнем уравнения.
Значит, не является корнем уравнения.
Иррациональные уравнения вида «дробь равна нулю».
Из этого утверждения вытекают два подхода к решению уравнений такого вида:
Найти ОДЗ исходного уравнения, решить уравнение , проверить корни на принадлежность ОДЗ. Этот случай удобнее использовать в тех случаях, когда найти область допустимых значений проще, чем решить уравнение .
Решить уравнение и проверить, какие из его корней являются решениями исходного уравнения. Этот случай используется, когда нахождение области допустимых значений затруднительно.
Найдём область допустимых значений уравнения.
Так как ОДЗ состоит только из одного числа, то осталось проверить, является ли это число корнем исходного уравнения.
. Значит, действительно является корнем исходного уравнения.
Нахождение области допустимых значений усложняется за счёт второго множителя в знаменателе. Поэтому решим сначала уравнение , а затем проверим найденные корни для исходного уравнения.
. Полученное выражение не имеет смысла, т.к. в знаменателе оказался нуль, значит, не является корнем исходного уравнения.
. Значит, является корнем исходного уравнения.
Приведение иррациональных уравнений к числовым равенствам.
Приведение иррациональных уравнений к неверным числовым равенствам.
В этом случае исходное уравнение корней не имеет.
Как видно, в результате равносильных преобразований, получилось неверное числовое равенство. Это означает, что исходное уравнение корней не имеет.
Ответ: корней нет.
Приведение иррациональных уравнений к верным числовым равенствам. Во время преобразований, ведущих к верному числовому равенству, необходимо следить за тем, что происходит с областью допустимых значений. Если она расширяется, то отсеиваем посторонние корни (в соответствии с ОДЗ); если область допустимых значений сужается, то лучше поискать другой способ решения данного уравнения.
Получилось верное равенство, значит, уравнение должно иметь бесконечно много корней. Однако, при использовании равносильных преобразований у нас расширилась область допустимых значений. Поэтому, необходимо найти ОДЗ исходного уравнения, это и будет его решением.
Переход к модулям может быть использован на основании одного из свойств корня: , где – любое действительное число. Такое преобразование является равносильным и ОДЗ не изменяется.
Воспользуемся определением модуля:
, значит, единственным корнем уравнения является .
Преобразование иррациональных уравнений. Выполняя преобразования при решении иррациональных уравнений, необходимо помнить, что есть преобразования, которые сохраняют область допустимых значений, а есть преобразования, которые изменяют ОДЗ. Рассмотрим возможные преобразования.
Замена выражений тождественно равными выражениями, не изменяющими ОДЗ.
К таким заменам относятся:
перестановка местами слагаемых и множителей в обеих частях уравнения;
раскрытие скобок в обеих частях уравнения;
группировка слагаемых (множителей) в обеих частях уравнения;
вынесение за скобки общего множителя;
замена числовых выражений их значениями;
выполнение действий с одночленами и многочленами, присутствующими в записи уравнения.
Обратите внимание , что приведение подобных слагаемых, сокращение дробей, замена нулём произведения или дроби с равным нулю числителем, может привести к изменению ОДЗ. Причём, появление посторонних корней можно откорректировать областью допустимых значений, а вот потерю корней откорректировать не получится. Поэтому, в таком случае, следует поискать другой способ решения уравнения.
На первый взгляд уравнение кажется достаточно простым и многим придёт на ум идея представить выражение в виде корня в квадрате . Тогда уравнение приобретает вид: . А теперь разберём, что мы получаем в этом случае. ОДЗ исходного уравнения: . После преобразования ОДЗ станет: . Мы получили сужение области допустимых значений, а это приводит к потере корней. Значит, такое преобразование выполнять нельзя.
Другие сделают другое преобразование: . Но такое преобразование не будет тождественно равным, т.к. , но никак не . Тогда, с учётом модуля, исходное уравнение будет представлено в виде системы двух уравнений, а это решение уже не будет оптимальным.
Значит, ищем другой подход к решению данного уравнения. Обращаем внимание на то, что в каждом из первых двух слагаемых присутствуют одинаковые выражения. Можно сделать замену переменной: , тогда и уравнение принимает вид:
Возвращаемся к исходной переменной:
Значит, – посторонний корень.
Аналогично проверяем остальные три значения х. Получаем, что – тоже посторонний корень. Значит, корнями исходного уравнения являются: и
Прибавление (или вычитание) одного и того же числа к обеим частям уравнения.
Это равносильное преобразование, оно не изменяет область допустимых значений.
Вычитаем из обеих частей уравнения .
Возводим в квадрат обе части уравнения.
Прибавление (вычитание) одного и того же выражения, не изменяющего ОДЗ, к обеим частям уравнения.
Вычитаем из обеих частей уравнения слагаемое и получаем уравнение:
Так как правая часть этого уравнения должна быть неотрицательной, то область допустимых значений не изменилась, т.е. преобразование равносильно. Возведём в квадрат обе части уравнения.
Перенесение слагаемых из одной части уравнения в другую с противоположным знаком.
Это преобразование всегда равносильное, область допустимых значений не изменяет.
Перенесём слагаемые в правую часть уравнения с противоположными знаками. Область допустимых значений не изменится.
Умножение (деление) обеих частей уравнения на одно и то же, отличное от нуля, число.
Это равносильное преобразование, не изменяет области допустимых значений и используется, обычно, для перехода от дробных чисел к целым.
Умножим обе части уравнения на , при этом ОДЗ не изменится.
Умножение (деление) обеих частей уравнения на одно и то же выражение, не изменяющее ОДЗ, и не равное в этой области нулю.
Это преобразование равносильно тогда, когда выражение, на которое умножают или делят, не изменяет область допустимых значений и не обращается на этой области в нуль. При использовании этого преобразования, необходимо следить за изменением ОДЗ.
Сразу отметим, что преобразование, которое приводит исходное уравнение к виду: не является равносильным, т.к. в этом случае сужается ОДЗ, что приводит к потере корней. Действительно, ОДЗ полученного уравнения:
Поэтому такое преобразование недопустимо.
Мы поступим по-другому. Так как , то умножим на это выражение обе части уравнения. Получим:
. Это преобразование не изменило ОДЗ.
В левой части раскроем скобки, а в правой – умножим дробь на выражение. Как мы выяснили ранее, эти преобразования опять-таки не меняют ОДЗ, значит, равносильные. .
Далее воспользуемся свойством корня из произведения и сокращением дробей. Это преобразование расширит ОДЗ, однако, мы сможем отсеять посторонние корни в соответствии с ОДЗ исходного уравнения.
Оба найденных корня принадлежат ОДЗ исходного уравнения, значит, они являются корнями исходного уравнения.
Возведение обеих частей уравнения в одну и ту же степень.
Это преобразование в общем случае не является равносильным, т.к. приводит к расширению ОДЗ, поэтому необходимо либо найти сразу ОДЗ, а затем отсеять посторонние корни, либо решить уравнение и в конце выполнить проверку найденных корней. Примеры таких преобразований присутствуют практически во всех ранее рассмотренных примерах.
На основании всего выше сказанного, подытожим:
производите равносильные преобразования;
следите за областью допустимых значений.
http://www.cleverstudents.ru/equations/irrational_equations.html
http://infourok.ru/irracionalnie-uravneniya-metodi-resheniya-3530431.html
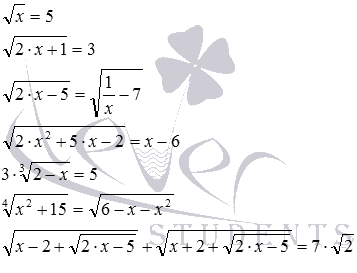

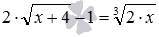 и
и 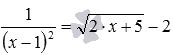 .
.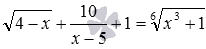 , также несложно обосновать убывание функции в левой части уравнения и возрастание функции в правой части уравнения.
, также несложно обосновать убывание функции в левой части уравнения и возрастание функции в правой части уравнения.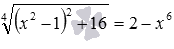 . Оценки его частей
. Оценки его частей 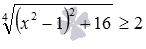 и
и 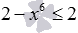 позволяют получить решение.
позволяют получить решение.