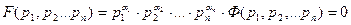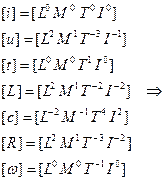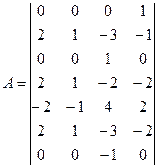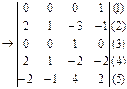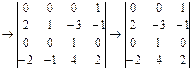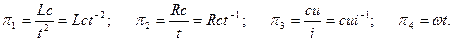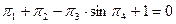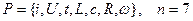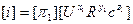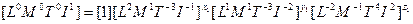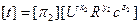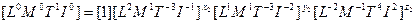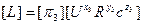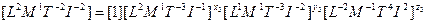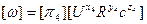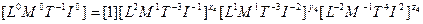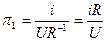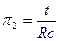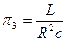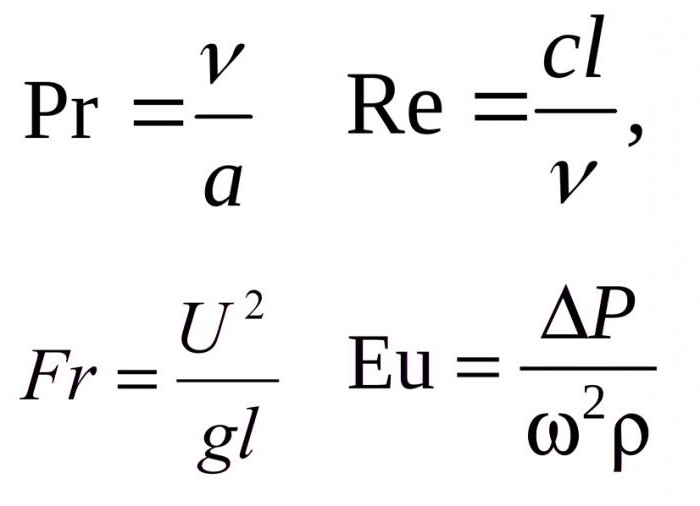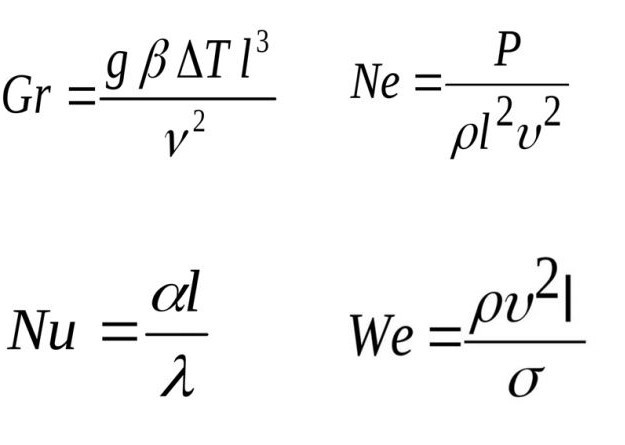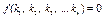Определение критериев подобия из уравнений процесса

Определение критериев подобия при известном

математическом описании

Пусть объект описывается уравнением (уравнение – размерная величина).

Любую размерную величину можно представить в виде произведения степенного комплекса размерной величины и безразмерной функции этих же величин.

Из свойств степенных комплексов безразмерная функция размерных величин может быть представлена в виде функции безразмерных степенных комплексов:

Если математическое описание группы заведомо подобных процессов известно и выглядит, например, как линейное дифференциальное уравнение,

(3.1)

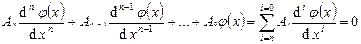
решение которого (общий интеграл имеет вид):

(3.2)

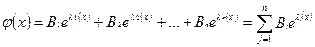
Для конкретного процесса u_c(t) изменения напряжения u_c во времени t на конденсаторе С в последовательной цепи из конденсатора и активного сопротивления R, которая включается на постоянное напряжение Е, при нулевых начальных условиях. При различных значениях R, C, и Е процессы u_c(t) заведомо будут иметь качественно одинаковый характер, что позволяет рассматривать их как группу подобных процессов. Переходный процесс описывается линейным дифференциальным уравнением:

(3.1а)

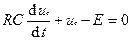
Решение которого имеет вид:

(3.2а)

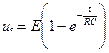
Согласно правилу Фурье все члены уравнения, описывающего какой — либо физический процесс, имеют одинаковую размерность. Поэтому уравнение можно привести к безразмерному виду, если разделить его на один из членов, здесь u_c:

,

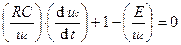
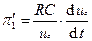
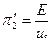
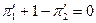
если обозначить и , то формула примет вид:

(3.3а)

Для подобных процессов соотношения пропорциональности справедливы и для «точечных» значений и для малых отклонений от этих параметров D:

С учетом (3.4a) можно записать p₁’ и p₂’ в виде:

(3.5а)

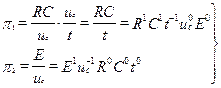
Выражения для p₁ и p₂, имеющие вид безразмерных степенных комплексов параметров, характеризующих рассматриваемый процесс, называются критериями подобия; критерии подобия численно одинаковы для сходственных точек подобных процессов.

Аналогично приводится к безразмерному виду (3.1) путем деления на первый член:

(3.3)

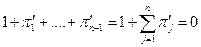
Преобразования аналогичные (3.5а), с учетом (3.4а) позволяют получить для (3.3) систему критериев подобия вида:

(3.4)

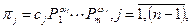
P₁, . P_m — параметры рассматриваемого процесса, ( P_i = x ); c_j, a_j, . w_j — безразмерные числа, принимающие некоторые действительные, в том числе нулевые, значения.

Критерии подобия имеют вид безразмерных степенных комплексов параметров, которые характеризуют процесс.

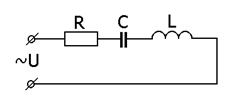Пример: Пусть процесс, происходящий в цепи представленной на рис.11 описывается уравнением:

Рис. 11 График процесса, происходящего в цепи

1 .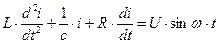

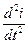
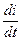
Тогда параметры, описывающие систему L, c, R, ω, i, u, t, и .

С точки зрения подобия (для вывода критерия подобия)

; .

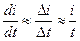
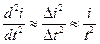
Замена 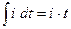называется “способ интегральных оценок”.

Способ интегральных оценок — способ определения критериев подобия по известному математическому описанию процесса путем приведения его к безразмерному виду, при котором символы дифференцирования и интегрирования в выражениях для определения критериев подобия опускаются.

Вообще, существует две системы критериев подобия: первая — получаемая из дифференциального уравнения, вторая — из решения (общего интеграла) дифференциального уравнения. Однако обе системы критериев подобия идентичны, т.к. имеют одинаковый физический смысл.

Таким образом, интеграл дифференциального уравнения можно представить в виде функции критериев подобия, но при этом констатируется только факт возможности получения такой зависимости, вид связей критериев не устанавливается.

Следовательно, в описании системы 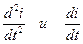— лишние параметры, тогда полный набор параметров P = , n=7.

Для определения количества критериев запишем размерность каждого параметра через основные единицы измерения L, M, T, I:

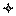
откидываем как независимую строку

(т.к. ранг матрицы определяется количеством независимых параметров).

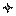
Откидываем как зависимые строки: (6) [(4)-(3) = (6)], [(2)-(1).3+(3)=(4)],

а также 2-ой столбец , тогда максимальный возможный ранг матрицы = 3.

Так как определитель матрицы ≠ 0, тогда ранг матрицы 3, соответственно количество независимых параметров k = 3, тогда количество критериев

Исходное уравнение перепишем с учетом способа интегральных оценок:

,

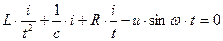
где каждое из слагаемых имеет одинаковую размерность.

Поделим уравнение на 2-ое слагаемое, получим:

,

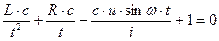
тогда критерии имеют вид:

Определение критериев подобия с использованием теории размерности

(при неизвестном математическом описании)

1 шаг: Выявление параметров Р_i, характеризующих процесс, .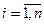

2 шаг:Составление полной матрицы размерности параметров Р_i (матрица А).

3 шаг:Определение количества зависимых и независимых параметров (k, m = n-k).

4 шаг:Любой зависимый параметр может быть представлен как

2 .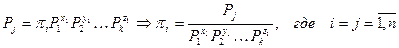

Если неизвестны математические описания процессов, критерии также можно получить. Для этого функциональную зависимость, полученную из эксперимента или расчета и имеющую в размерных физических величинах P₁, . P_j, . P_m вид:

Или, для рассмотренного примера F(u_c, t, R, C, E) = 0 можно представить как

Для определения критериев подобия в данном случае применяется метод анализа размерностей физических величин P_j, определяющих характер процесса. Возможность установления критериев подобия, когда вид функциональной зависимости неизвестен, создает предпосылки для представления данных экспериментального исследования в обобщенной форме и распространения результатов единичного эксперимента на группу или класс подобных процессов.

Допустим, что в качестве основных единиц измерения выбраны [a b …q], тогда

размерность 1-го параметра ,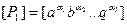

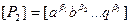
2-го параметра ,

n-го параметра 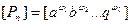, где l- количество единиц измерения.

Рассмотрим уравнение 2 с точки зрения размерности.

— уравнение для p₁,

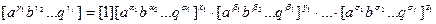
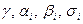
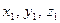
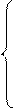
где — известные, — неизвестные величины.

g₁ = a₁x₁ + b₁y₁ +… + s₁z₁

Решив эти уравнения, находим критерии подобия по формулам:

, , … .

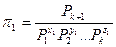
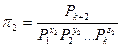
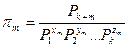
Пример: Математическое описание не известно.

1.Определим по методике вектор параметров

2,3 пункты см. выше k =3, m =4.

Группа независимых параметров (можно выбрать любые): [U, R,c].

Группа зависимых параметров [I, t, L, w].

По формуле находим 4 критерия подобия:

, , , .

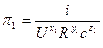
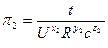
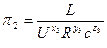
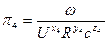
Определим p₁:

Получим систему уравнений

Так как 1 и 2 уравнения зависимые, то получим следующую совместную систему:

x₁ + y₁ — z₁ = 0 x₁ = 1

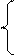
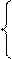
Определим p₂:

Получим систему уравнений

Так как 1 и 2 уравнения зависимые, то получим следующую совместную систему:

x₂ + y₂ — z₂ = 0 x₂ = 0

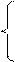
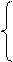
Определим p₃:

Получим систему уравнений

Так как 1 и 2 уравнения зависимые, то получим следующую совместную систему:

x₃ + y₃ — z₃ = 1 x₃ = 0

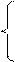
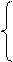
Определим p₄:

Получим систему уравнений

Так как 1 и 2 уравнения зависимые, то получим следующую совместную систему:

x₄ + y₄ — z₄ = 0 x₄ = 0

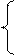
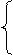
Найдем виды критериев по формуле:

,

.

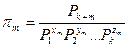
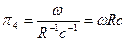
Рассмотренные положения относятся к случаю заведомо подобных процессов, т.е. определяют необходимые условия существования подобия. В связи с этим возникает вопрос об условиях, не только необходимых, но и достаточных для существования подобия. Такие обстоятельства, кроме равенства критериев, включают в себя требования подобия начальных и граничных условий сопоставляемых процессов.

Положения относительно необходимых и достаточных условий подобия изложены в виде первой, второй и третьей теорем о подобии, первые две — определяют необходимые, третья — необходимые и достаточные условия подобия.

Основные теоремы теории подобия

Теория подобия включает три основные теоремы: 1-ая теорема подобия (Теорема Ньютона-Бертранса) о небходимом условии подобия, 2-ая теорема подобия (Пи-теорема), 3-ая теорема подобия (Теорема Кирпичова-Гухмана) о необходимом и достаточном условии подобия.

Дата добавления: 2015-11-10 ; просмотров: 861 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Критерий подобия: определение и примеры

Слово «критерий» греческого происхождения, означает признак, являющийся основой для формирования оценки объекта или явления. На протяжении последних лет широко используется как в научной среде, так и в образовании, управлении, экономике, сфере обслуживания, в социологии. Если критерии научности (это определенные условия и требования, обязательные к соблюдению) представлены в абстрагированной форме для всего научного сообщества, то критерии подобия затрагивают только те области науки, которые имеют дело с физическими явлениям и их параметрами: аэродинамикой, теплообменом и массообменом. Для того чтобы разобраться в практической ценности применения критериев, необходимо изучить некоторые понятия из категориального аппарата теории. Стоит отметить, что критерии подобия использовались в технических специальностях задолго до того, как получили свое название. Самым тривиальным критерием подобия можно назвать нахождение процента от целого. Подобную операцию проделывали все без особых проблем и сложностей. А коэффициент полезного действия, который отражает зависимость потребляемой мощности машины и отдаваемой, всегда являлся критерием подобия и от этого не стал восприниматься как нечто туманно-заоблачное.

Основания возникновения теории

Физическое подобие явлений, будь то природа или рукотворный технический мир, применяется человеком в исследованиях по аэродинамике, массо- и теплообмену. В научной среде неплохо зарекомендовал себя метод исследования процессов и механизмов при помощи моделирования. Естественно, что при планировании и проведении эксперимента опорой является энергодинамическая система величин и понятий (ЭСВП). Следует сделать оговорку, что система величин и система единиц (СИ) не равнозначны. На практике ЭСВП существует в окружающем мире объективно, и исследования лишь выявляют их, поэтому основные величины (или критерии физического подобия) не обязаны совпадать с основными единицами. А вот основные единицы (систематизированные в СИ), отвечая требованиям практики, утверждаются (условно) при помощи международных конференций.

Понятийный аппарат подобий

Теория подобия — понятия и правила, целью которых является определение подобия процессов и явлений и обеспечение возможности переноса исследуемых явлений с опытного образца на реальный объект. Основу терминологического словаря составляют такие понятия, как однородные, одноименные и безразмерные величины, константа подобия. Для облегчения понимания сути теории следует рассмотреть значение перечисленных терминов.

• Однородные — величины, которые имеют равные физический смысл и размерность (выражение, показывающее, каким образом единица измерения данной величины составляется из единиц основных величин; скорость имеет размерность длины, разделённой на время).
• Одноименные — процессы, которые различаются по значению, но имеют одинаковую размерность (индукция и взаимоиндукция).
• Безразмерные — величины, в размерность которых основные физические величины входят в степени, равной нулю.

Константа — безразмерная величина, в которой базовой является величина с фиксированным размером (например, элементарный электрический заряд). Она позволяет произвести переход от модели к натуральной системе.

Основные виды подобия

Подобными могут быть любые физические величины. Принято выделять четыре вида:

• геометрическое (наблюдается при равенстве отношений сходных линейных размеров образца и модели);
• временное (наблюдается на сходных частицах подобных систем, двигающихся по подобным путям за определенный промежуток времени);
• физических величин (можно наблюдать на двух сходных точках модели и образца, для которых соотношение физических величин будет постоянным);
• начальных и граничных условий (можно наблюдать при соблюдении трех предыдущих подобий).

Инвариант подобия (обычно обозначается idem в расчетах и обозначает инвариантно или «такой же») – это выражение величин в относительных единицах (т. е. отношение сходных величин в рамках одной системы).

В том случае, если инвариант содержит отношения однородных величин, его называют симплексом, а если разнородных величин, то критерием подобия (им присущи все свойства инвариантов).

Законы и правила теории подобия

В науке все процессы регулируются при помощи аксиом и теорем. Аксиоматическая составляющая теории включает три правила:

• значение h величины H такое же, как отношение величины к единице ее измерения [H];
• физическая величина независима от выбора единицы ее измерения;
• математическое описание явления не подчиняется конкретному выбору единиц измерения.

Основные постулаты

При помощи теорем описаны следующие правила теории:

• Теорема Ньютон-Бертрана: для всех подобных процессов все исследуемые критерии подобия попарно равны друг другу (π₁*=π₁**; π₂*=π₂** и т. д.). Отношение критериев двух систем (модели и образца) всегда равно 1.
• Теорема Бэкингема-Федермана: критерии подобия связаны при помощи уравнения подобия, которое представляется безразмерным решением (интегралом) и называется критериальным уравнением.
• Теорема Киринчен-Гухмана: для подобия двух процессов необходимы качественная их равнозначность и попарная равнозначность определяющих критериев подобия.
• Теорема π (иногда именуется Бэкингема или Ваши): взаимосвязь между h величинами, которые измеряются при помощи m единиц измерения, представляется в виде отношения h – m безразмерными сочетаниями π₁,…, π_h-m этих h величин.

Критерий подобия – это комплексы, объединенные при помощи π–теоремы. Вид критерия можно установить при помощи составления списка величин (A₁,…, A_n) описывающих процесс, и применить рассматриваемую теорему к зависимости F(a₁,…,a_n)=0, являющейся решением задачи.

Критерии подобия и методы исследования

Бытует мнение, что наиболее точно описывающее название теории подобия должно звучать как метод обобщенных переменных, поскольку она является одним из способов обобщения в науке и экспериментальных исследованиях. Основными сферами влияния теории являются методы моделирования и аналогии. Использование основных критериев подобия как частной теории существовало задолго до введения этого термина (ранее назывались коэффициентами или степенями). В качестве примера можно привести тригонометрические функции всех углов подобных треугольников – они безразмерны. Они представляют пример геометрического подобия. В математике самым известным критерием является число Пи (отношение размеров окружности и диаметра круга). На сегодняшний день теория подобия является широко распространенным орудием научных исследований, которое качественно преобразовывается.

Физические явления, изучаемые посредством теории подобия

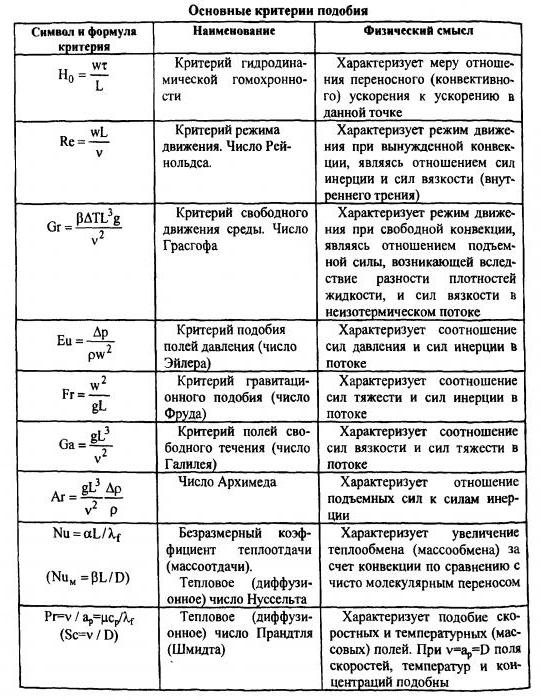
В современном мире трудно представить изучение процессов гидродинамики, теплообмена, массообмена, аэродинамики в обход теории подобий. Критерии выводятся для любых явлений. Главное, что между их переменными существовала зависимость. Физический смысл критериев подобия отражается в записи (формуле) и предшествующих ей вычислениях. Обычно критерии, как и некоторые законы, называются в честь знаменитых ученых.

Изучение теплообмена

Критерии теплового подобия состоят из величин, которые способны описать процесс теплоотдачи и теплообмена. Наиболее известных критериев четыре:

В формуле представлены следующие величины:

• с – скорость носителя тепла;
• l – геометрический параметр (размер);
• v – коэффициент кинематической вязкости

При помощи критерия установлена зависимость сил инерции и вязкости.

В него входят такие составляющие:

• α – является коэффициентом теплоотдачи;
• l – геометрический параметр (размер);
• λ – является коэффициентом теплопроводности.

Данный критерий описывает зависимость между интенсивностью теплоотдачи и проводимостью теплоносителя.

• Критерий Прандтля (Pr)

В формуле представлены следующие величины:

• v – является коэффициентом кинематической вязкости;
• α – является коэффициентом температуропроводности.

Данный критерий описывает соотношение температурных и скоростных полей в потоке.

Формула составлена при помощи таких переменных:

• g – обозначает ускорение земного притяжения;
• β – является коэффициентом объемного расширения теплоносителя;
• ∆T – обозначает разность температур между теплоносителем и проводником.

Данный критерий описывает соотношение двух сил молекулярного трения и подъемной силы (происходит благодаря разной плотности жидкости).

Критериями подобия теплообмена при свободной конвенции обычно называются критерии Нуссельта, Грасгофа и Прандтля, а при вынужденной конвенции – Пекле, Нуссельта, Рейнольдса и Прандтля.

Изучение гидродинамики

Критерии гидродинамического подобия представлены следующими примерами.

В формуле представлены следующие величины:

• υ – обозначает скорость вещества на расстоянии от обтекаемого ею предмета;
• l – описывает геометрические (линейные) параметры предмета;
• g – обозначает ускорение силы тяжести.

Данный критерий описывает соотношение сил инерции и тяжести в потоке вещества.

• Критерий подобия Струхаля (St).

Формула содержит такие переменные:

• υ – обозначает скорость;
• l – обозначает геометрические (линейные) параметры;
• Т – обозначает интервал времени.

Данный критерий описывает неустановившиеся движения вещества.

В формуле представлены следующие величины:

• υ – обозначает скорость вещества в конкретной точке;
• с – обозначает скорость звука (в жидкости) в конкретной точке.

Данный критерий гидродинамического подобия описывает зависимость движения вещества от его сжимаемости.

Кратко об остальных критериях

Перечислены наиболее встречающиеся критерии физического подобия. Не менее важными являются такие как:

• Вебера (We) – описывает зависимость сил поверхностного натяжения.
• Архимеда (Ar) – описывает зависимость подъемных сил и инерции.
• Фурье (Fo) – описывает зависимость скорости изменения температурного поля, физических свойств и размеров тела.
• Померанцева (Po) – описывает соотношения интенсивности внутренних источников теплоты и температурного поля.
• Пекле (Pe) – описывает соотношения конвективного и молекулярного переносов теплоты в потоке.
• Гидродинамической гомохронности (Ho) – описывает зависимость переносного (конвективного) ускорения и ускорения в данной точке.
• Эйлера (Eu) — описывает зависимость сил давления и инерции в потоке.
• Галилея (Ga) – описывает соотношение сил вязкости и тяжести в потоке.

Заключение

Критерии подобия могут состоять из определенных величин, но могут выводиться и из других критериев. И такая комбинация также будет являться критерием. Из приведенных примеров видно, что принцип подобия является незаменимым в гидродинамике, геометрии, механике, существенно упрощая в некоторых случаях процесс исследования. Достижения современной науки стали возможными во многом благодаря возможности моделировать сложные процессы с большой точностью. Благодаря теории подобия, было сделано не одно научное открытие, отмеченное затем Нобелевской премией.

Теория подобия и критериальные уравнения

Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. Попытки аналитического решения полной системы уравнений наталкиваются на серьезные трудности. Поэтому большое значение приобретает экспериментальный путь исследования. Однако при изучении столь сложного процесса, как конвективный теплообмен, не всегда легко проводить и опытное исследование.

Для исследования влияния на процесс какой-либо одной величины остальные нужно сохранять неизменными, что не всегда возможно или затруднительно из-за большого количества переменных. Кроме того, нужно быть уверенным, что результаты, получаемые с помощью какой-либо конкретной установки (модели), можно перенести и на другие аналогичные процессы (образец). Эти трудности помогает разрешить теория подобия. С помощью теории подобия размерные физические величины можно объединить в безразмерные комплексы, причем так, что число комплексов будет меньше числа величин. Полученные безразмерные комплексы можно рассматривать как новые переменные.

При введении в уравнения безразмерных комплексов число величин под знаком искомой функции формально сокращается, что упрощает исследование физических процессов.

Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому. Ввиду этого теория подобия является теоретической базой эксперимента, но не только. Теория подобия является важным подспорьем теоретических исследований. Хотя методами теории подобия вид искомой функции не может быть определен, эта теория облегчает в ряде случаев анализ процесса и описание полученных результатов.

Для практического использования выводов теории подобия необходимо уметь приводить к безразмерному виду математические описания изучаемых процессов.

Имеется несколько методов, и один из них — метод масштабных преобразований.

независимые переменные: х, у.

зависимые переменные:

постоянные величины: и др. Для определенной задачи они являются постоянными.

Таким образом, искомые зависимые переменные 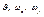зависят от большого числа величин: они являются функцией независимых переменных и постоянных величин.

В качестве масштабов удобно принять постоянные величины .

; ; ; ; , тогда

; ; ; ; .

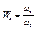
Помимо безразмерных величин и безразмерных координат X, Y, составленных из однородных физических величин, в уравнения входят также безразмерные комплексы, состоящие из разнородных физических величин.

Безразмерные соотношения параметров характеризующих процесс, имеющие у подобных явлений в сходственных точках численно одинаковые значения называются числами подобия.

1). У подобных явлений числа подобия численно одинаковы.

2). Интеграл дифференциальной функции (или системы уравнений) может быть представлен как функция чисел дифференциального уравнения.

3). Подобны те явления, условия однозначности которых подобны, и числа подобия, составленные из условия однозначности, численно одинаковы.

Условия однозначности: Явление, протекающее в геометрически подобных системах; для рассматривания явления можно составить дифференциальные уравнения; установлены существование и единственность решения уравнений при заданных граничных условиях; известны числовые значения коэффициентов и физических параметров.