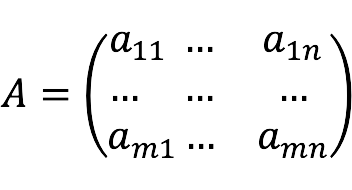Определение основной матрицы системы линейных алгебраических уравнений

Системы линейных алгебраических уравнений: основные понятия, виды

Определение СЛАУ

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

$$\left\<\begin a_ <11>\cdot x_<1>+a_ <12>\cdot x_<2>+\ldots+a_ <1 n>\cdot x_=b_ <1>\\ a_ <21>\cdot x_<1>+a_ <22>\cdot x_<2>+\ldots+a_ <2 n>\cdot x_=b_ <2>\\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots . . \\ a_ \cdot x_<1>+a_ \cdot x_<2>+\ldots+a_ \cdot x_=b_ \end\right.$$

Упорядоченный набор значений $$\left\^<0>, x_<2>^<0>, \ldots, x_^<0>\right\>$$ называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

Задание. Проверить, является ли набор $<0,3>$ решением системы $\left\<\begin 3 x-2 y=-6 \\ 5 x+y=3 \end\right.$

Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$:

$$5 x+y=3 \Rightarrow 5 \cdot 0+3=3 \Rightarrow 3=3$$

Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.

Ответ. Набор $<0,3>$ является решением системы $\left\<\begin 3 x-2 y=-6 \\ 5 x+y=3 \end\right.$

Виды систем

СЛАУ называется совместной, если она имеет, хотя бы одно решение.

В противном случае система называется несовместной.

Система $\left\<\begin 3 x-2 y=-6 \\ 5 x+y=3 \end\right.$ является совместной, так как она имеет, по крайней мере, одно решение $x=0$, $y=3$

Система $\left\<\begin 5 x+y=-6 \\ 5 x+y=3 \end\right.$ является несовместной, так как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Ни для каких наборов $$ это не выполняется.

Система называется определённой, если она совместна и имеет единственное решение.

В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.

Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.

Система называется квадратной, если количество уравнений равно количеству неизвестных.

Система $\left\<\begin 3 x-2 y=-6 \\ 5 x+y=3 \end\right.$ квадратная, так как неизвестных две и это число равно количеству уравнений системы.

Матричная запись систем уравнений

Исходную СЛАУ можно записать в матричном виде:

Задание. Систему $\left\<\begin x-y+z-4 t=0 \\ 5 x+y+t=-11 \end\right.$ записать в матричной форме и выписать все матрицы, которые ей соответствуют.

Решение. Заданную СЛАУ записываем в матричной форме $A. X=B$ , где матрица системы:

$$A=\left(\begin 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end\right)$$

то есть, запись СЛАУ в матричной форме:

$$\left(\begin 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end\right)\left(\begin x \\ y \\ z \\ t \end\right)=\left(\begin 0 \\ -11 \end\right)$$

Расширенная матрица системы

Задание. Записать матрицу и расширенную матрицу системы $\left\<\begin 2 x_<1>+x_<2>-x_<3>=4 \\ x_<1>-x_<2>=5 \end\right.$

Решение. Матрица системы $A=\left(\begin 2 & 1 & -1 \\ 1 & -1 & 0 \end\right)$ , тогда расширенная матрица $\tilde=(A \mid B)=\left(\begin 2 & 1 & -1 & 4 \\ 1 & -1 & 0 & 5 \end\right)$

Система линейных алгебраических уравнений

В данной публикации мы рассмотрим определение системы линейных алгебраических уравнений (СЛАУ), как она выглядит, какие виды бывают, а также как ее представить в матричной форме, в том числе расширенной.

Определение системы линейных уравнений

Система линейных алгебраических уравнений (или сокращенно “СЛАУ”) – это система, которая в общем виде выглядит так:

Индексы коэффициентов ( a_ij ) формируются следующим образом:

• i – номер линейного уравнения;
• j – номер переменной, к которой относится коэффициент.

Решение СЛАУ – такие числа c₁, c₂,…, c_n , при постановке которых вместо x₁, x₂,…, x_n , все уравнения системы превратятся в тождества.

Виды СЛАУ

1. Однородная – все свободные члены системы равны нулю ( b₁ = b₂ = … = b_m = 0 ).
   

В зависимости от количества решений, СЛАУ может быть:

1. Совместная – имеет хотя бы одно решение. При этом если оно единственное, система называется определенной, если решений несколько – неопределенной.
   
   СЛАУ выше является совместной, т.к. есть хотя бы одно решение: , y = 3 .
2. Несовместная – система не имеет решений.
   
   Правые части уравнений одинаковые, а левые – нет. Таким образом, решений нет.

Матричная форма записи системы

СЛАУ можно представить в матричной форме:

• A – матрица, которая образована коэффициентами при неизвестных:
  
• X – столбец переменных:
  
• B – столбец свободных членов:
  

Пример
Представим систему уравнений ниже в матричном виде:

Пользуясь формами выше, составляем основную матрицу с коэффициентами, столбцы с неизвестными и свободными членами.

Полная запись заданной системы уравнений в матричном виде:

Расширенная матрица СЛАУ

Если к матрице системы A добавить справа столбец свободных членов B , разделив данные вертикальной чертой, то получится расширенная матрица СЛАУ.

Для примера выше получается так:

– обозначение расширенной матрицы.

Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений с неизвестными называется система уравнений вида

Числа называются коэффициентами системы ; — свободными членами , — неизвестными . Количество уравнений в системе может быть меньше, больше или равно числу неизвестных.

Решением системы называется упорядоченная совокупность чисел такая, что после замены неизвестных соответственно числами каждое уравнение системы превращается в верное числовое равенство. Система называется совместной , если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной .

Система (5.1) называется однородной , если все свободные члены равны нулю:

В отличие от однородной, систему общего вида (5.1) называют неоднородной .

Систему (5.1) принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы

свободные члены записываем в столбец свободных членов

а неизвестные — в столбец неизвестных

Матричная запись неоднородной системы уравнений (5.1) имеет вид

Матричную запись (5.3) системы уравнений можно представить в эквивалентной форме

Тогда решение системы представляется столбцом и удовлетворяет равенству

т.е. столбец свободных членов является линейной комбинацией столбцов матрицы системы.

Относительно системы уравнений нас интересуют ответы на следующие вопросы:

1. Совместна система или нет?

2. Если система совместна, то имеет ли она единственное решение или нет?

3. Если решение единственное, то как его найти?

4. Если система имеет бесконечно много решений, то какова структура множества решений?

5. Как в бесконечном множестве решений системы определить одно решение, наилучшее с практической точки зрения?

6. Если система несовместна, то как определить ее приближенное решение?

Правило Крамера

Рассмотрим случай, когда число уравнений равно числу неизвестных , т.е. систему

где матрица системы — квадратная n-го порядка:

Ее определитель обозначим

Теорема 5.1 (правило Крамера). Если определитель матрицы системы линейных уравнений с неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам

где — определитель матрицы, полученной из матрицы системы заменой i-го столбца столбцом свободных членов, т.е.

В самом деле, рассмотрим систему (5.6) как матричное уравнение . Так как определитель матрицы отличен от нуля, по теореме 4.2 заключаем, что матричное уравнение имеет единственное решение:

где — обратная матрица. Запишем i-й элемент столбца , учитывая, что в i-й строке присоединенной матрицы стоят алгебраические дополнения i-го столбца матрицы

Заметим, что в скобках записано разложение определителя по i-му столбцу, т.е. , что и требовалось доказать.

1. На практике при больших правило Крамера не применяется, так как вычисление определителя n-го порядка требует большого числа арифметических операций. Поэтому применяются более экономичные алгоритмы. Обычно, правило Крамера используется, когда нужно найти только несколько неизвестных (например, одну) среди многих. В теоретических исследованиях правило Крамера незаменимо и используется весьма продуктивно.

2. Если и хотя бы один определитель , то система несовместна. Если , то возможны два случая: либо система несовместна, либо имеет бесконечно много решений.

Пример 5.1. Решить систему линейных уравнений с помощью правила Крамера

Решение. Составим матрицу системы . Вычислим ее определитель

Так как определитель отличен от нуля, система имеет единственное решение (см. теорему 5.1). Находим определители и неизвестные

Условие совместности системы линейных уравнений

Рассмотрим систему (5.3) линейных уравнений с неизвестными. Составим блочную матрицу, приписав к матрице справа столбец свободных членов. Получим расширенную матрицу системы :

Эта матрица содержит всю информацию о системе уравнений, за исключением обозначений неизвестных.

Теорема 5.2 Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы: .

Необходимость следует из равенства (5.5) и следствия 1 теоремы 3.3. Если система имеет решение, то столбец свободных членов есть линейная комбинация столбцов матрицы системы. Поэтому при вычеркивании столбца Ь из расширенной матрицы ее ранг не изменяется. Следовательно, .

Для доказательства достаточности нужно использовать теорему о базисном миноре. Из равенства следует, что базисный минор матрицы является базисным минором расширенной матрицы . Поэтому столбец является линейной комбинацией столбцов базисного минора матрицы , а, значит, и всех столбцов матрицы . Следовательно, существуют числа , удовлетворяющие условию (5.5), т.е. система совместна.

Замечание 5.2. Теорема Кронекера-Капелли дает лишь критерий существования решения системы, но не указывает способа отыскания этого решения.

Пример 5.2. Определить, имеет ли система уравнений решения

Решение. Составим матрицу системы и расширенную матрицу системы

Ранг матрицы равен 2, так как она имеет не равные нулю миноры второго порядка и третья строка этой матрицы равна сумме первых двух строк. Следовательно, третью строку можно вычеркнуть, при этом ранг матрицы не изменится. Ранг расширенной матрицы равен трем, так как она имеет не равный нулю минор третьего порядка, например, минор, составленный из первого, второго и последнего столбцов расширенной матрицы

Следовательно, . Поэтому система несовместна (не имеет решений).