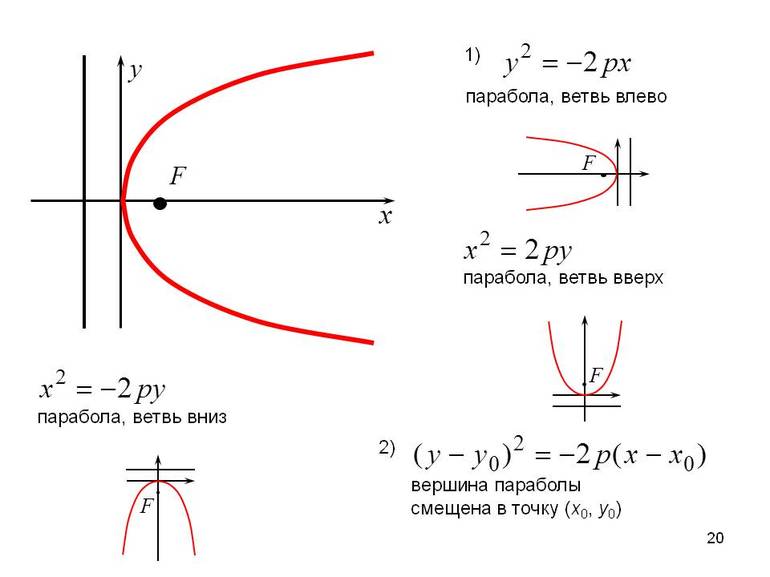
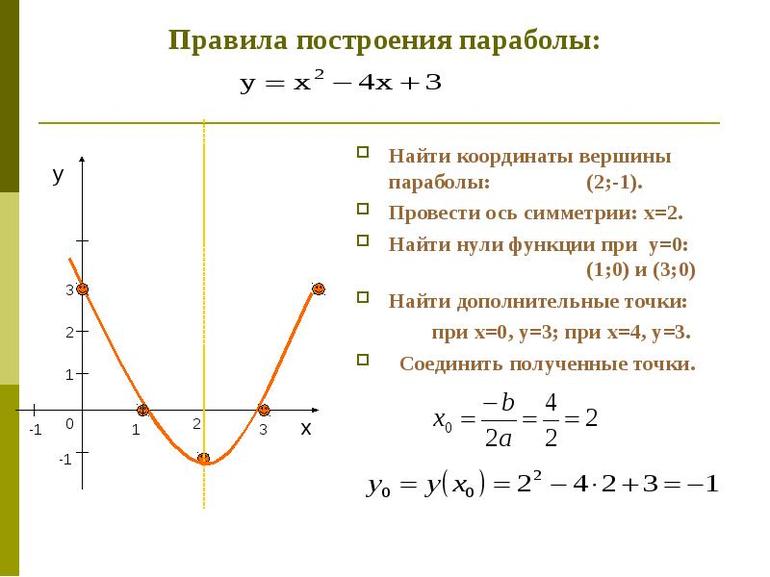
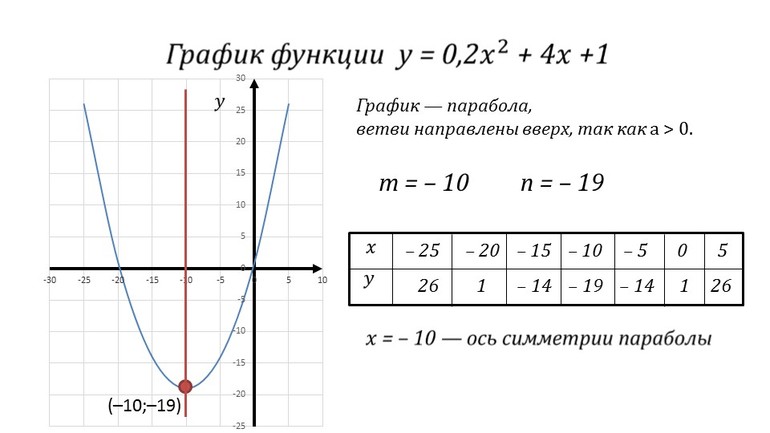
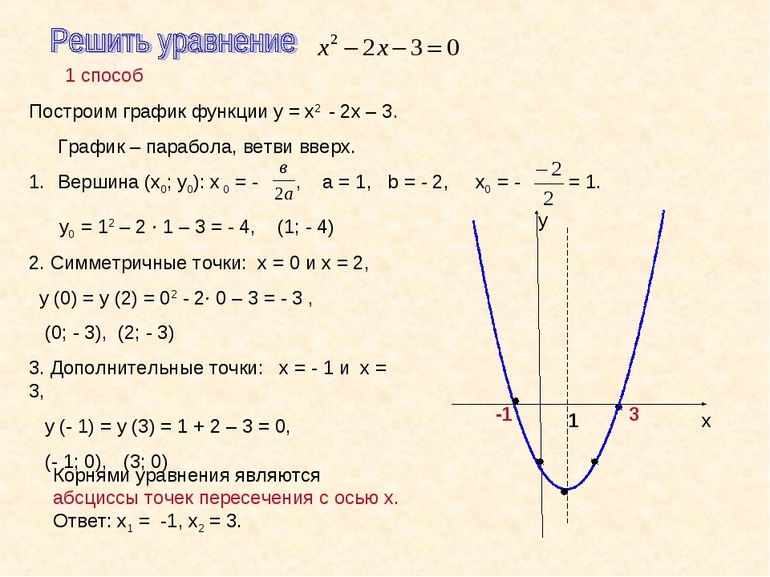
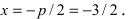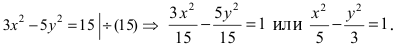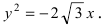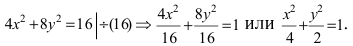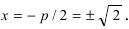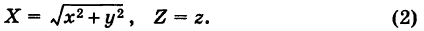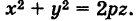Парабола — определение и вычисление с примерами решения
Парабола:
Определение: Параболой называется геометрическое место точек равноудаленных от выделенной точки F, называемой фокусом параболы, и прямой (l), называемой директрисой.
Получим каноническое уравнение параболы. Выберем декартову систему координат так, чтобы фокус F лежал на оси абсцисс, а директриса проходила бы через точку, расположенную симметрично фокусу, перпендикулярно к оси абсцисс (Рис. 34). Пусть точка M(х; у) принадлежит параболе: Вычислим расстояния от точки M(х; у) до фокуса и директрисы
Рис. 34. Парабола, (уравнение директрисы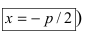
Возведем обе части уравнения в квадрат
Раскрывая разность квадратов, стоящую в правой части уравнения, получим каноническое уравнение параболы: 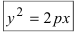
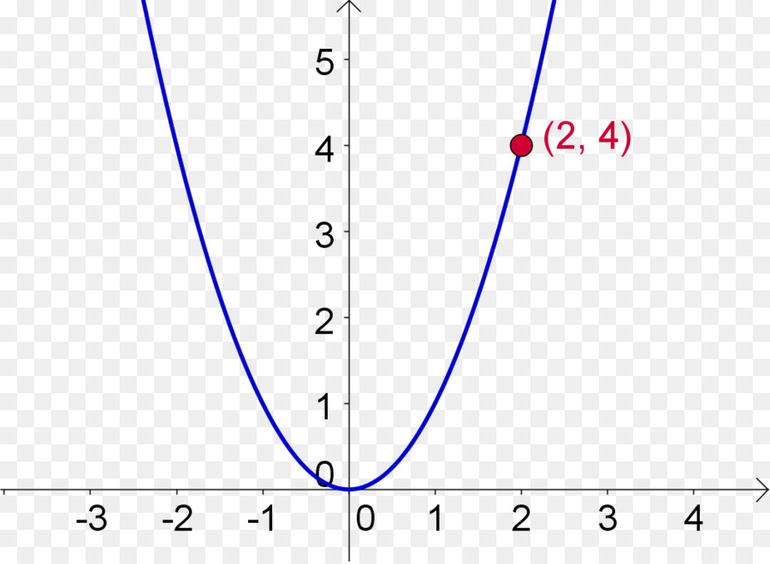
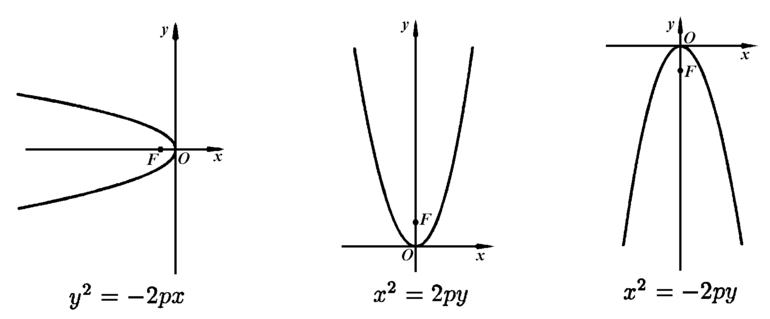
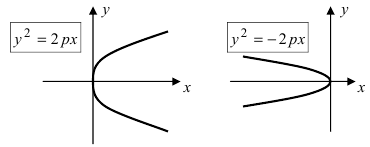
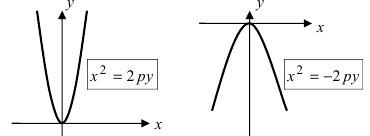
Рис. 35а. Параболы и их уравнения.
Рис. 356. Параболы и их уравнения.
Найдем координаты точек пересечения параболы с координатными осями:
— точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью ординат.
Определение: Точка О(0; 0) называется вершиной параболы.
Если точка М(х; у) принадлежит параболе, то ей принадлежат и точка 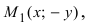
Пример:
Дано уравнение параболы 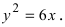
Решение:
Так как из уравнения параболы 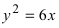
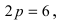
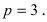
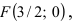
Пример:
Составить каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат, а параметр р равен расстоянию от фокуса гиперболы 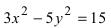
Решение:
Для определения координат фокусов гиперболы преобразуем её уравнение к каноническому виду.
Гипербола:
Следовательно, действительная полуось гиперболы 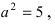
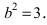
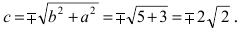
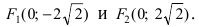
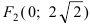
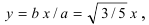
Следовательно, каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат имеет вид:
Пример:
Составить каноническое уравнение параболы, фокус которой совпадает с одним из фокусов эллипса 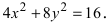
Решение:
Для определения координат фокусов эллипса преобразуем его уравнение к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса 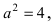
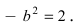
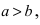
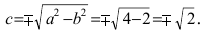
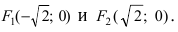
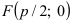
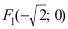
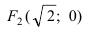

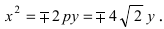
Уравнение параболоида вращения
Пусть вертикальная парабола
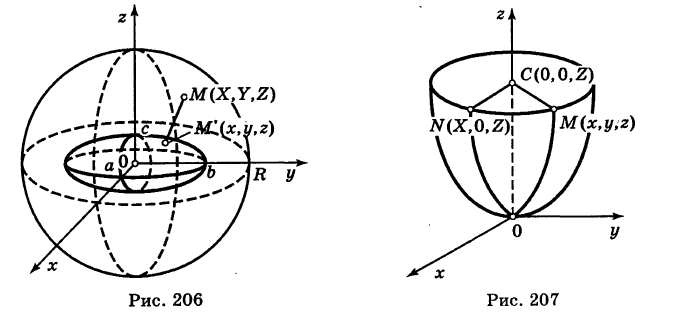
расположенная в плоскости Охz, вращается вокруг своей оси (ось Oz). При вращении получается поверхность, носящая название параболоида вращения (рис. 207).
Для вывода уравнения поверхности рассмотрим произвольную точку 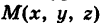
Так как точки М и N расположены в одной и той же горизонтальной плоскости и CN = СМ как радиусы одной и той же окружности, то имеем
Подставляя формулы (2) в уравнение (1), получим уравнение параболоида вращения
Заметим, что форму параболоида вращения имеет поверхность ртути, находящейся в вертикальном цилиндрическом сосуде, быстро вращающемся вокруг своей оси. Это обстоятельство используют в технике для получения параболических зеркал.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Многогранники
- Окружность
- Эллипс
- Гипербола
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Парабола
Парабола, её форма, фокус и директриса.
Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^<2>=2px\label
$$
при условии \(p > 0\).
Из уравнения \eqref
Форма параболы известна из курса средней школы, где она встречается в качестве графика функции \(y=ax^<2>\). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством \(2p=a^<-1>\).
Фокусом параболы называется точка \(F\) с координатами \((p/2, 0)\) в канонической системе координат.
Директрисой параболы называется прямая с уравнением \(x=-p/2\) в канонической системе координат (\(PQ\) на рис. 8.11).
Рис. 8.11. Парабола.
Свойства параболы.
Расстояние от точки \(M(x, y)\), лежащей на параболе, до фокуса равно
$$
r=x+\frac
<2>.\label
$$
Вычислим квадрат расстояния от точки \(M(x, y)\) до фокуса по координатам этих точек: \(r^<2>=(x-p/2)^<2>+y^<2>\) и подставим сюда \(y^<2>\) из канонического уравнения параболы. Мы получаем
$$
r^<2>=\left(x-\frac
<2>\right)^<2>+2px=\left(x+\frac
<2>\right)^<2>.\nonumber
$$
Отсюда в силу \(x \geq 0\) следует равенство \eqref
Заметим, что расстояние от точки \(M\) до директрисы также равно
$$
d=x+\frac
<2>.\nonumber
$$
Следовательно, мы можем сделать следующий вывод.
Для того чтобы точка \(M\) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.
Докажем достаточность. Пусть точка \(M(x, y)\) одинаково удалена от фокуса и от директрисы параболы:
$$
\sqrt<\left(x-\frac
<2>\right)^<2>+y^<2>>=x+\frac
<2>.\nonumber
$$
Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы \eqref
Параболе приписывается эксцентриситет \(\varepsilon=1\). В силу этого соглашения формула
$$
\frac
$$
верна и для эллипса, и для гиперболы, и для параболы.
Уравнение касательной к параболе.
Выведем уравнение касательной к параболе в точке \(M_<0>(x_<0>, y_<0>)\), лежащей на ней. Пусть \(y_ <0>\neq 0\). Через точку \(M_<0>\) проходит график функции \(y=f(x)\), целиком лежащий на параболе. (Это \(y=\sqrt<2px>\) или же \(y=-\sqrt<2px>\), смотря по знаку \(y_<0>\).) Для функции \(f(x)\) выполнено тождество \((f(x))^<2>=2px\), дифференцируя которое имеем \(2f(x)f'(x)=2p\). Подставляя \(x=x_<0>\) и \(f(x_<0>)=y_<0>\), находим \(f'(x_<0>)=p/y_<0>\) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_<0>=\frac
$$
Упростим его. Для этого раскроем скобки и вспомним, что \(y_<0>^<2>=2px_<0>\). Теперь уравнение касательной принимает окончательный вид
$$
yy_<0>=p(x+x_<0>).\label
$$
Заметим, что для вершины параболы, которую мы исключили, положив \(y_ <0>\neq 0\), уравнение \eqref
Касательная к параболе в точке \(M_<0>\) есть биссектриса угла, смежного с углом между отрезком, который соединяет \(M_<0>\) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).
Рассмотрим касательную в точке \(M_<0>(x_<0>, y_<0>)\). Из уравнения \eqref
$$
(\overrightarrow
<2>y_<0>+py_<0>=y_<0>(x_<0>+\frac
<2>).\nonumber
$$
Но \(|\overrightarrow
Заметим, что \(|FN|=|FM_<0>|\) (см. рис. 8.12).
Парабола — свойства, формулы и примеры построения
Основные определения
Параболой называется кривая второго порядка, состоящая из множества точек, которые удалены на равные расстояния от директрисы и вершины. Ее еще называют функцией квадратичного типа. Не следует путать с гиперболой, поскольку она является прямой второго порядка, но ее называют кубической.
Директриса — условная прямая, относительно которой строится кубическая парабола. Она не указывается на чертеже, но полезна при нахождении неизвестных параметров, когда требуется выполнить дополнительное построение.
Вершина (фокус) — ближайшая точка к директрисе. Из нее исходят симметричные ветви кривой, на которой располагаются точки, имеющие одинаковое значение ординат, а их абсциссы равны между собой по модулю и являются противоположными числами.
Полезные свойства
Парабола, как и любое геометрическое тело, обладает определенными свойствами:
- Ветви проходят в зависимости от коэффициента, стоящего перед аргументом старшей степени A: A 0 — вверх.
- Геометрическая фигура, принадлежащая к кривым ll порядка.
- Симметричность.
- Изделия, изготовленные в форме параболы, всегда отражают свет, аккумулируя его в одной точке — вершине.
- Отрезок, соединяющий среднюю точку хорды и точку, где пересекаются прямые-касательные, всегда перпендикулярен директрисе.
- Подобие всех кубических парабол.
Свойства помогают находить некоторые параметры кривой, доказывать утверждения и теоремы. Однако этого недостаточно для решения задач. Следует разобрать математические формы записи параболы.
Формула кривой
Формула параболы — математическая запись, описывающая ее поведение в пространстве. В физико-математических дисциплинах описаны 3 основные формы: каноническая, квадратичная и общая. В первом случае уравнение выглядит у^2=2nх, где у — ордината, х — абсцисса и n — параметр, равный отрезку между директрисой и вершиной кривой.
Следует отметить, что р>0. Чтобы вывести формулу параболы, следует применить алгоритм:
- Записать формулу директрисы. Она параллельна OУ (ординате): х+n/2=0.
- Координаты вершины — (n/2;0).
- Отметить произвольную точку М на одной из ветвей кривой, а затем соединить с вершиной (фокусом — F). В результате получится отрезок FМ.
- Длина FM: FM=[(х-n/2)^2+у^2]^0.5.
- Также FМ записывается при помощи такого тождества: х+n/2.
- Поставить знак равенства между тождествами в четвертом и пятом пунктах: х+n/2=[(х-n/2)^2+у^2]^0.5.
- Возвести обе части во вторую степень, а затем привести подобные коэффициенты: y^2 = 2pn.
Вторая форма математической записи — квадратичная функция. Последняя имеет вид обыкновенного квaдратного трехчлена, т. е. y=Ах^2+Bx+C, где А, В и С — некоторые коэффициенты. Иногда формула рассматривается без дополнительных элементов В и С, т. е. y= ax^2 . В этом случае вершина кривой II порядка находится по формулам:
- Абсцисса: х=-B/2A.
- Ордината: у=-D/2A, где D — значение дискриминанта D=(-B)^2 — 4AC.
Третье представление (уравнение параболы) — общее. Его можно править следующим образом: Ах^2+Вху+Су^2+Dх+Еу+F = 0. Некоторые коэффициенты могут быть эквивалентны нулю. Кроме того, кривая задается также в полярной системе при помощи соотношения n(1+cos(s))=n. В последнем равенстве параметр «n» эквивалентен отрезку, соединяющему директрису и вершину.
Методы нахождения координат вершины
Очень часто функция квадратичного типа при решении задач может быть представлена в некотором виде, который следует при помощи математических преобразований привести в читабельную форму. Последний термин обозначает, что требуется преобразовать формулу параболы для удобного построения таблицы и схематического представления. Делается эта операция по следующему алгоритму на примере z=t^2 +4t+2:
- Приравнять к нулевому значению (квадратное уравнение): t^2 +4t+2=0.
- Выполнить подготовительную операцию по выделению квадрата: t^2 +4t+2+2=0.
- Выделить формулу сокращенного умножения — квадрат: (t+2)^2 -2=0.
- Перенести «-2» вправо, т. е. (t+2)^2=2.
- Найти вершину исходя из решения тождества без «-2».
- Определить ординату z: z=-(2), т. е. число из правой части выражения, умноженное на -1.
- Вычислить координату фокуса (смещение относительно начала координат): (t;z)=(-2;-2).
Методика позволяет найти фокус без дополнительных формул. Однако существует и другой способ определения вершины, где применяется производная функции:
- Определить производную: z’=2t+4.
- Приравнять z’ к нулевому значению: 2t+4=0.
- Найти корень: t=-2.
- Подставить в первоначальную функцию для нахождения ординаты, т. е. z=-2.
- Координата вершины: (-2;-2). Она совпадает со значением в предыдущем примере.
Существуют программные продукты для нахождения параметров параболы. Названия имеют английскую номенклатуру, т. е. «parabola».
График функции
Иногда требуется в заданиях графическое представление функции. Для этого необходимо следовать инструкции:
- Найти вершину любым из способов.
- Рассчитать координаты точек, в которых происходит пересечение с ординатами и абсциссами в прямоугольной системе координат.
- Построить вспомогательную таблицу. Специалисты рекомендуют использовать для схематического построения не менее 4 точек, не считая вершины, а для точного — не менее 10. Кроме того, вершина всегда находится посередине значений таблиц.
- Отметить каждую точку, а затем соединить плавными линиями.
График параболы хорош тем, что позволяет освободиться от большого количества расчетов, поскольку является симметричным. Для таблицы зависимостей достаточно подставить 2 одинаково противоположные величины, а иногда и разные числа превращают значения функции в одинаковые величины.
В первом случае для уравнения z=f^2+1 возможно взять 2 значения аргумента «f» — 1 и -1. При подстановке их в формулу z не изменится, т. е. z1=2 и z2=2. Во втором — 5 и 7 могут давать значение функции, равное 8.
Пример решения
Для практического применения теоретических знаний о параболе рекомендуется решать задачи. Условие одной из них формулируется следующим образом: дана формула функции параболы f=(t+2)^2 -3t^2+8t-5+3(t-1)^2, для которой необходимо подготовить данные, чтобы построить график в схематическом виде (8 значений). Решать ее следует по следующей методике:
- Раскрыть скобки и привести подобные элементы: f=t^+4t-1.
- Приравнять к 0: t^2+4t-1=0.
- Выделить квадрат: (t+2)^2-5.
- Перенос свободного члена: (t+2)^2=5.
- Вершина с координатами: (-2;-5).
- Вычислить нули функции с абсциссами: t^2+4t-1=0. Корни: t1=-2-(5)^0.5 и t2=-2+(5)^0.5. Координаты: (-2-(5)^0.5;0) и (-2+(5)^0.5;0)
- Нули функции (пересечение оси ординат при t=0): (0+2)^2-5=-1. Координата — (0;-1).
- Построение таблицы.
| f | -5 | -3 | -1 | 0 | -5 | 0 | -1 | -3 | -5 |
| t | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
Можно приступать к построению графика. Специалисты рекомендуют чертить его при помощи карандаша. Отмечать следует только точки, указанные в таблице. Кроме того, необходимо указать на графике нули функции, а также ее пересечения с ординатой. Ветви искомой параболы будут направлены вверх, поскольку коэффициент при квадрате 1>0.
Таким образом, парабола — кривая ll порядка, которая используется для описания некоторых физических явлений, траекторий движения тел в пространстве, а также для описания квадратичной зависимости между двумя величинами.
http://univerlib.com/analytic_geometry/second_order_lines_and_surfaces/parabola/
http://nauka.club/matematika/parabol%D0%B0.html
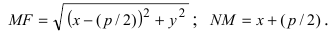
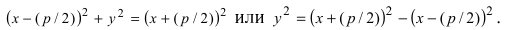
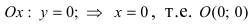 — точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью абсцисс;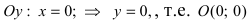 — точка пересечения параболы с осью ординат.
— точка пересечения параболы с осью ординат.