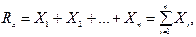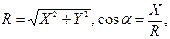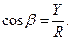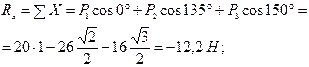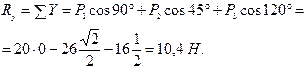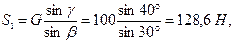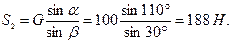Аналитическое определение равнодействующей
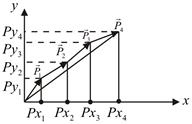
Равнодействующую системы сходящихся сил можно определить и аналитически (способом проекций). Для этого необходимо воспользоваться теоремой: проекция равнодействующей на данную ось равна алгебраической сумме проекций слагаемых сил на ту же ось.
Проекции равнодействующей на координатные оси х и у определяются как суммы проекций составляющих.

Для удобства и простоты индекс и пределы суммирования ставить не будем:
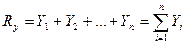
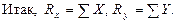
Зная проекции, определяют модуль и направление равнодействующей по формулам:
При решении задач на сложение плоской системы сходящихся сил аналитическим способом необходимо: выбрать систему координатных осей х и у;найти углы каждой силы с координатными осями, а затем, определив проекции равнодействующей, найти ее модуль и направление.
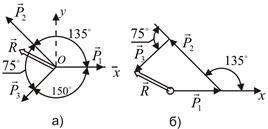
Пример 4.Даны силы P1 = 20 Н, P2 = 26 Н, P3 = 16 Н, приложенные к точке О. Силы составляют между собой следующие углы: 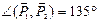
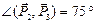
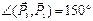
Определить равнодействующую 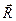



|
|
|
|
|
|
|
Решение. Примем точку О за начало координат, линию действия силы 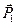
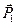
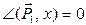
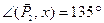
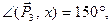
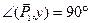
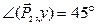
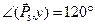
Определим проекции равнодействующей:
Тогда модуль и направление равнодействующей равны:
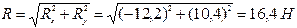
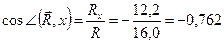
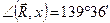
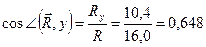
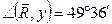
Этот же результат можно получить и геометрически, построив в определенном масштабе силовой многоугольник (рис. 4.12, б).
Метод проекции при решении задач на равновесие системы особенно удобен в том случае, если в систему входит более трёх сил.
4.6. Геометрическое и аналитическое условия
равновесия системы сходящихся сил
Необходимым и достаточным условием равновесия плоской системы сходящихся сил является равенство нулю равнодействующей этой системы сил. Это условие можно выразить одним векторным равенством:
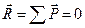
или двумя алгебраическими (скалярными) равенствами:
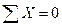
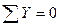
Векторное равенство выражает условие замкнутости многоугольника данных сил, т.е. условие равновесия плоской системы сходящихся сил в геометрической форме (4.10).
Равенства выражают условие равновесия плоской системы сходящихся сил в аналитической форме (4.11), и их называют условиями равновесия плоской системы сходящихся сил: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на координатные оси были равны нулю.
Методические указания к решению задач
геометрическим способом
При решении задач геометрическим (графическим) способом необходимо придерживаться следующего порядка.
1. Выделить тело (или точку), равновесие которого следует рассмотреть.
2. Изобразить все активные (заданные) силы, действующие на выделенное тело.
3. Освободить это тело от наложенных на него связей, заменив их действие реакциями связей.
4. Построить замкнутый силовой многоугольник (или треугольник, если действуют три силы). При этом следует сначала сложить все заданные, а затем достроить неизвестные силы.
5. Решить силовой многоугольник (по известным элементам определить неизвестные) или, если силовой многоугольник построен в масштабе, определить искомые силы по масштабу.
Методические указания к решению задач
аналитическим способом
При решении задач аналитическим способом рекомендуется придерживаться следующего порядка.
1. Выделить тело (или точку), равновесие которого следует рассмотреть.
2. Изобразить активные (заданные) силы, действующие на выделенное тело.
3. Освободить тело от наложенных на него связей, заменив их действие реакциями связей.
4. Выбрать систему координат. Координатные оси следует по возможности направлять по неизвестным силам, тогда проекция неизвестной силы на перпендикулярную ей ось окажется равной нулю. Благодаря этому в уравнение равновесия войдет только одно неизвестное.
5. Составить уравнения равновесия плоской системы сил: 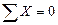
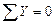
6. Решить уравнения равновесия относительно искомых величин.
Преимущества аналитического способа проекций перед геометрическим способом силового многоугольника особенно заметны в задачах на равновесие системы более трёх сил. Действительно, решение силового четырёх-, пяти- и n-угольника представляет известные трудности, в то время как решение методом проекций не усложняется при увеличении числа проектируемых сил.
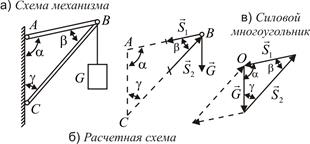
Пример 5. В шарнире В кронштейна ABC подвешен груз весом G = 100 Н. Определить усилия в стержнях кронштейна, если a = 110°, b = 30°, g = 40°. Стержни прикреплены к стене шарнирно (рис. 4.13, а).
|
|
|
Решение. Рассмотрим равновесие шарнира В (рис. 4.13, б). К нему приложена активная сила 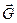
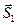
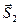
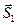
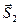
Для решения применим геометрический способ. Поскольку шарнир находится в равновесии, то силовой треугольник, составленный из этих сил, должен быть замкнут. Из некоторой точки О (рис. 4.13, в) в выбранном масштабе строим вектор 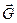
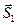
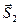
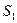
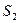
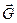
Модули 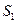
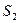
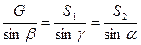
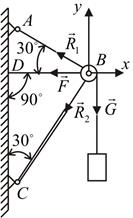
Пример 6. На оси шарнира В свободно вращается блок (рис. 4.14). Через блок перекинута нить, с помощью которой удерживается груз весом G = 50 Н. Определить усилия в стержнях АВ и ВС. При этом диаметром блока, трением нити можно пренебречь.
Решение. Для решения применим аналитический метод.
1. Выделим точку, равновесие которой следует рассмотреть: в данной задаче это будет точка В неподвижного блока.
2. Изобразим векторы всех активных сил, действующих на нее: в нашем примере это натяжение вертикальной ветви нити и натяжение горизонтальной ветви нити, равные весу груза.
3. Мысленно отбросим связи и заменим их реакциями 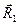
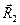
4. Все силы изобразим в виде векторов, предположив, что стержни АВ и ВС растянуты, направив соответственно 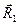
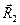
Выбрав направление координатных осей х и у,составим два уравнения равновесия:
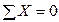
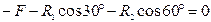
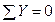
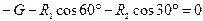
Рис. 4.14. Шарнирно-стержневая система
Учитывая, что F = G = 50 Н, решив совместно оба уравнения, получим R1= – 18,6 Н; R2= – 68,5 Н. Здесь знак «–» указывает на то, что стержни АВ и ВС сжаты, а не растянуты, как мы предполагали ранее.
Контрольные вопросы
1. Как влияет угол между двумя сходящимися силами на модуль их равнодействующей?
2. Какие условия необходимы для того, чтобы задача разложения силы на две составляющие была определённой?
3. Для чего и как строится силовой многоугольник?
4. В чем заключается геометрическое условие равновесия плоской системы сходящихся сил?
5. Чему равна проекция силы на ось?
6. В каких случаях проекция силы на ось равна нулю, и в каких случаях она равна модулю силы?
7. Как определяется знак проекции силы на ось?
8. Как найти модуль и направление силы, если известны ее проекции на две взаимно перпендикулярные оси координат?
9. В чем заключаются аналитические условия равновесия плоской системы сходящихся сил?
Дата добавления: 2015-12-26 ; просмотров: 15138 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Техническая механика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
- 1. Аксиомы и понятие силы статики
- 2. Связи и реакции связей
- 3. Определение равнодействующей геометрическим способом
- 4. Определение равнодействующей аналитическим способом
- 5. Пара сил. Момент силы
Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
4. Определение равнодействующей аналитическим способом
Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.
Проекция силы на две взаимно перпендикулярные оси.
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.
Модуль (величину) равнодействующей можно определить по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской системы сходящихся сил:
При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
Плоская система сходящихся сил
Содержание:
Плоская система сходящихся сил – это система сил линии действия которых сходятся в одной точке, называются сходящимися.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Плоская система сходящихся сил — основные понятия и определения
Если все силы, приложенные к телу, расположенные в одной плоскости и линии их действия пересекаются в одной точке, то такая система сил носит название плоской системы сходящихся сил.
Покажем на рис. 1.6 произвольное тело, к которому приложена плоская системы сходящихся сил 



Определение равнодействующей системы сходящихся сил
Геометрический способ сложения сил:
Добавить систему сил означает определить их равнодействующую. Попробуем найти равнодействующую для плоской системы сходящихся сил, которая изображена на
рис. 1.6. Возьмем (условно) две первые силы 

статики найдем их равнодействующую 


сторонах, построим свой параллелограмм, диагональ которого, которая приложена в
точке A, и является их равнодействующей 


параллелограмм, диагональ которого будет второй равнодействующей 


Если внимательно присмотреться к геометрическому построению параллелограммов, то можно увидеть, что к концу вектора силы 




Таким образом, геометрический способ добавления сходящихся сил сводится к построению силового многоугольника. Он строится путем параллельного переноса векторов сил в масштабе, когда начало следующей силы совпадает с концом предыдущей силы. Тогда вектор равнодействующей соединяет начало первой силы с концом последней силы. Это можно записать так:
Величина равнодействующей силы не изменится, если будет изменен порядок
присоединения (добавление) сил до многоугольника, но конфигурация силового
многоугольника будет другой.
Условие равновесия плоской системы сходящихся сил в геометрической форме
Если к свободному материальному телу приложена одна сила, то о равновесии этого тела речи не может быть. Таким образом, если рассматривать плоскую систему сходящихся сил, которая сведена к равнодействующей, то тело не может быть в равновесии.
Для равновесия тела под действием плоской системы сходящихся сил необходимо и
достаточно, чтобы равнодействующая всех сил была равна нулю.
Равнодействующая такой системы сил будет равна нулю, когда силовой многоугольник будет замкнутым, то есть когда начало вектора первой силы будет совпадать с концом вектора последней силы.
Теорема о равновесии тела под действием трех не параллельных сил
Если тело под действием системы трех плоских не параллельных сил находится в равновесии, то линии действия этих сил пересекаются в одной точке.
Представим тело (рис. 1.7), к которому в точках А, B, C приложены силы





Далее, если есть в точке О две приложенные силы, то на основании III аксиомы статики их можно заменить одной силой, то есть равнодействующей 






Проекция силы на ось и на плоскость
Представим силу 

Обозначим сначала конце вектора силы 


По знаку проекция силы на ось тогда будет положительная, когда угол α (угол пересечения направления вектора силы или линии действия силы с осью) острый. В полной мере разумеется, если этот угол равен в 90º, то проекция силы 

Но практически тут удобнее использовать тупой угол α2, а острый угол β между вектором силы 
Таким образом, проекция силы на ось — это направленный отрезок на оси, образованный между перпендикулярами, которые опущены из концов вектора силы на ось, и который по величине равен произведению модуля силы на косинус угла между направлением вектора силы и осью.
Спроектируем теперь вектор силы на плоскость и оси координат.
Возьмем силу 




где α — угол между вектором силы 
Следует заметить, что проекция вектора силы на плоскость является вектором, потому что плоскость на имеет базисных векторов, ортов.
Если в плоскости xOy обозначить угол β, то есть возможность спроектировать силу 

В данном случае через ось z и вектор силы 
где ϒ — угол между вектором силы 
Определение силы за ее проекциями
Предположим, что у нас в плоскости рисунка имеем прямоугольную декартову систему координат Oxy, заданные две проекции силы — 


На заданных проекциях, как на сторонах, строим прямоугольник, диагональ которого, проходит через точку пересечения проекций, и является искомым вектором силы 

Углы между вектором силы 
Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.
Аналогично для пространственной системы сил (рис. 1.9) можно построить на проекциях сила как на сторонах параллелепипед, а модуль силы 
Направление вектора этой силы также определяется через направляющие косинусы его углов с соответствующими осями координат x, y и z:
Через арккосинус определяют сами углы.
Теорема о проекции равнодействующей силы на ось
Проекция вектора равнодействующей силы на ось равна алгебраической сумме проекций векторов составляющих сил на ту же ось.
Доказательство. Имеем систему сил 




Добавим алгебраически все проекции и подсчитаем, почему эта сумма равна:
Но отрезок ak и является проекцией равнодействующей силы 
Аналитический способ добавления системы сходящихся сил
На основании теоремы о проекции равнодействующей силы на ось, имеем:
Аналогично проекция равнодействующей силы на ось y будет равняться
Модуль равнодействующей равен
Углы между вектором равнодействующей 
Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.
Условия равновесия тела под действием плоской системы сходящихся сил в аналитической форме
Плоскую систему сходящихся сил можно заменить одной силой, которая носит название равнодействующей.
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы равнодействующая была равна нулю. А если равнодействующая равна нулю, то и ее проекции на оси x и y тоже должны равняться нулю. Поскольку проекции
равнодействующей равны алгебраическим суммам проекций составляющих сил, то,
окончательно, иметь условия равновесия тела под действием плоской системы
сходящихся сил
Для равновесия тела, находящегося под действием плоской системы сходящихся
сил, необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси
координат были равны нулю.
Услуги по теоретической механике:
Учебные лекции:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://kartaslov.ru/%D0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%90%D1%83%D1%80%D0%B8%D0%BA%D0%B0_%D0%9B%D1%83%D0%BA%D0%BE%D0%B2%D0%BA%D0%B8%D0%BD%D0%B0_%D0%A2%D0%B5%D1%85%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BC%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0_%D0%A8%D0%BF%D0%B0%D1%80%D0%B3%D0%B0%D0%BB%D0%BA%D0%B0/4
http://natalibrilenova.ru/ploskaya-sistema-shodyaschihsya-sil/