Определить число вещественных корней уравнения

Алгоритм расчёта вещественных корней полиномов

Основополагающая идея этого алгоритма очень проста и может быть изложена двумя предложениями. Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома. Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.

А теперь по порядку.

Проблема нахождения корней алгебраических полиномов известна давно, по крайней мере со средневековья. В школе учат решать квадратные уравнения. В википедии можно найти формулы Кардано для решения кубических уравнений и описание метода Феррари для решения в радикалах уравнения четвёртой степени. Там же описан метод Лобачевского для решения алгебраических уравнений произвольной степени. Суть метода Лобачевского вкратце сводится к следующему.

Нетрудно, имея некоторый исходный полином, построить полином2, имеющий те же по модулю корни, что и исходный полином, но с противоположным знаком. Перемножая исходный полином и полином2, получаем полином, корни которого равны квадратам корней исходного полинома.

Это преобразование (квадрирование) полезно повторить несколько раз. В результате, если корни исходного полинома не были равны друг другу, их многократно квадрированные значения оказываются далеко разнесёнными по величине, а их приближенные значения очень просто выражаются через коэффициенты соответствующего квадрированного полинома.

В частности, если коэффициент при старшей степени аргумента полинома равен единице, то следующий по старшинству коэффициент равен (с обратным знаком) сумме корней уравнения, а поскольку значения этих корней сильно разнесены, то приближенно можно считать эту сумму равной наибольшему по модулю корню.

Для конкретности сообщим, что для полинома 4-й степени с корнями 1, 2, 3, 4 метод Лобачевского уже после четвёртого квадрирования даёт правильные до второго знака после запятой значения корней. При этом для представления коэффициентов полиномов достаточно формата long double.

Бесспорно, этот метод является ценным инструментом в руках исследователя, наделённого интеллектом. Однако, его программирование для современной вычислительной техники вызывает серьёзные затруднения при необходимости строгой гарантии достоверности результата при всевозможных особых случаях расположения корней.

Теперь я начну описывать иной метод. В общедоступной печати упоминание о нём начинается с работы [1]. Какие-либо независимые публикации о применении такого метода мне неизвестны. Этот алгоритм сводится к последовательному исследованию интервалов монотонного изменения исходного полинома. Если на границах этого интервала монотонности значения полинома имеют разные знаки, то запускается процедура деления отрезка пополам для расчёта точного значения очередного корня. Границами интервалов монотонности являются точки, в которых значение производной полинома обращается в нуль, т.е. это корни производного полинома. Производный полином имеет степень на единицу меньшую, чем исходный полином, и процесс расчёта коэффициентов производных полиномов следует продолжить до полинома первой степени, корень которого находится непосредственно, без привлечения процедуры деления отрезка пополам. В результате этого шага получим два интервала монотонного изменения для производного полинома второй степени.

Теперь можно найти два вещественных корня производного полинома второй степени (если они существуют) и далее по лестнице из производных полиномов подниматься до корней исходного полинома. Остаётся пояснить, как технически реализуются границы «плюс, минус бесконечность» интервалов монотонности исходного и производных полиномов.

Нормируем полином так, чтобы коэффициент при старшей степени аргумента стал равным единице. Пусть M — наибольшее по модулю значение среди его остальных коэффициентов. Тогда значение полинома больше единицы для всех значений аргумента, больших, чем M+1.

Для доказательства рассмотрим расчёт полинома p(x)=x^n+k[n-1]*x^(n-1)+. +k[1]*x+k[0] по схеме Горнера.

На первом шаге вычисляется p[1]=k[n-1]+x и очевидно, что p[1]>1.
На втором шаге вычисляется p[2]=k[n-2]+x*p[1] и вновь очевидно, что p[2]>1.
Аналогичное имеет место на последующих шагах.
На последнем шаге вычисляется p(x)=k[0]+x*p[n-1] и окончательно получим p(x)>1.

Таким образом, если нужно определить знак полинома при бесконечном значении аргумента, следует взять аргумент равным M+1.

Прилагаемый текст соответствующей программы вполне заменяет занудное изложение отдельных технических подробностей описанного тут алгоритма.

Прокомментирую, наконец, не вполне очевидную особенность реализации алгоритма деления отрезка пополам.

Пробная точка pt, расположенная посередине между текущими концами ng и vg отрезка, вычисляется оператором pt=0.5*(ng+vg); а цикл делений пополам прерывается оператором if(pt =vg)break;.

В силу конечной точности представления вещественных чисел в машине рано или поздно наступает состояние, при котором операция деления пополам вместо нового числа даёт значение одной из исходных границ. Именно в этом состоянии следует прекратить цикл делений пополам. Это состояние соответствует максимально достижимой точности результата.

Недавно мне удалось использовать этот алгоритм для решения задачи вычисления комплексного корня полинома, не имеющего вещественных корней. Но об этом я планирую рассказать на Хабре в следующей статье.

Ниже, как приложение, приведен полный текст файла polynomRealRoots.cpp, реализующего описанныйалгоритм.

Примите также текст заголовочного файла polynomRealRoots.h, позволяющего легко организовать ссылку на приведенный выше программный модуль.

Литература

1. Костин И.К. Семейство алгоритмов расчета интервалов прохождения космического аппарата над круговым наземным объектом с учетом продольной ошибки определения параметров орбиты

Вопросы радиоэлектроники, сер. РЛТ, 2004г., вып. 1

Эту ссылку можно найти в Яндексе поиском по закавыченной фразе «семейство алгоритмов расчета», но текст этой статьи в электронном виде, кажется, недоступен. Поэтому приведу здесь цитату из двух предложений этой статьи:

Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома.

Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.

Применение производной для решения нелинейных уравнений и неравенств

п.1. Количество корней кубического уравнения

Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. \begin f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+bx+c \end Если в уравнении \(f'(x)=0\) дискриминант \(D=4b^2-12ac=4(b^2-3ac)\gt 0\), кубическая парабола имеет две точки экстремума: \(x_<1,2>=\frac<-2b\pm\sqrt><6a>\). Если при этом значения функции в точках экстремума \(f(x_1)\cdot f(x_2)\lt 0\), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но \(f(x_1)\cdot f(x_2)=0\), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.

Пример 1. Сколько корней имеют уравнения:

1) \(x^3+3x^2-4=0\) \(b^2-3ac=9\gt 0 (c=0) \) \(f(x)=x^3+3x^2-4 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=-4,\ f(x_2)=0 \) \(f(x_1)\cdot f(x_2)=0\Rightarrow\) два корня	2) \(x^3+3x^2-1=0\) \(b^2-3ac=9\gt 0 \) \(f(x)=x^3+3x^2-1 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=-1,\ f(x_2)=3 \) \(f(x_1)\cdot f(x_2)\lt 0\Rightarrow\) три корня
3) \(x^3+3x^2+1=0\) \(b^2-3ac=9\gt 0\) \(f(x)=x^3+3x^2+1 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=1,\ f(x_2)=5 \) \(f(x_1)\cdot f(x_2)\gt 0\Rightarrow\) один корень	4) \(x^3+x^2+x+3=0\) \(b^2-3ac=1-3\lt 0 \) Один корень

п.2. Количество корней произвольного уравнения

Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.

Пример 2. а) Найдите число корней уравнения \(\frac 1x+\frac<1>+\frac<1>\)
б) Найдите число корней уравнения \(\frac 1x+\frac<1>+\frac<1>=k\)

Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью \(y=1\). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=\frac1x+\frac<1>+\frac<1> $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: \(x\ne\left\<0;1;3\right\>\)
Все три точки – точки разрыва 2-го рода. \begin \lim_\left(\frac1x+\frac<1>+\frac<1>\right)=-\infty-1-\frac13=-\infty\\ \lim_\left(\frac1x+\frac<1>+\frac<1>\right)=+\infty-1-\frac13=+\infty\\ \lim_\left(\frac1x+\frac<1>+\frac<1>\right)=1-\infty-\frac12=-\infty\\ \lim_\left(\frac1x+\frac<1>+\frac<1>\right)=1+\infty-\frac12=+\infty\\ \lim_\left(\frac1x+\frac<1>+\frac<1>\right)=\frac13+\frac12-\infty=-\infty\\ \lim_\left(\frac1x+\frac<1>+\frac<1>\right)=\frac13+\frac12+\infty=+\infty \end 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные \(x=0, x=1, x=3\) – точки разрыва 2-го рода
2. Горизонтальные: \begin \lim_\left(\frac1x+\frac<1>+\frac<1>\right)=-0-0-0=-0\\ \lim_\left(\frac1x+\frac<1>+\frac<1>\right)=+0+0+0=+0\\ \end Горизонтальная асимптота \(y=0\)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: \(k=0\), нет.
4) Первая производная $$ f'(x)=-\frac<1>-\frac<1><(x-1)^2>-\frac<1><(x-3)^2>\lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.

5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.

6) Точки пересечения с OY – нет, т.к. \(x=0\) – асимптота
Точки пересечения с OX – две, \(0\lt x_1\lt 1,1\lt x_2\lt 3\)

7) График

Получаем ответ для задачи (а) 3 корня.

Решаем более общую задачу (б). Передвигаем горизонталь \(y=k\) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При \(k\lt 0\) — три корня
При \(k=0\) — два корня
При \(k\gt 0\) — три корня

Ответ: а) 3 корня; б) при \(k=0\) два корня, при \(k\ne 0\) три корня.

Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ \sqrt+\sqrt<10-2x>=a $$ имеет по крайней мере одно решение.

Исследуем функцию \(f(x)=\sqrt+\sqrt<10-2x>\)
ОДЗ: \( \begin x-1\geq 0\\ 10-2x\geq 0 \end \Rightarrow \begin x\geq 1\\ x\leq 5 \end \Rightarrow 1\leq x\leq 5 \)
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: \(f(1)=0+\sqrt<8>=2\sqrt<2>,\ f(5)=\sqrt<4>+0=2\)
Первая производная: \begin f'(x)=\frac<1><2\sqrt>+\frac<-2><2\sqrt<10-2x>>=\frac<1><2\sqrt>-\frac<1><\sqrt<10-2x>>\\ f'(x)=0\ \text<при>\ 2\sqrt=\sqrt<10-2x>\Rightarrow 4(x-1)=10-2x\Rightarrow 6x=14\Rightarrow x=\frac73\\ f\left(\frac73\right)=\sqrt<\frac73-1>+\sqrt<10-2\cdot \frac73>=\sqrt<\frac43>+\sqrt<\frac<16><3>>=\frac<6><\sqrt<3>>=2\sqrt <3>\end Промежутки монотонности:

Можем строить график:

\(y=a\) — горизонтальная прямая.
Количество точек пересечения \(f(x)\) и \(y\) равно количеству решений.
Получаем:

По крайней мере одно решение будет в интервале \(2\leq a\leq 2\sqrt<3>\).

п.3. Решение неравенств с построением графиков

Пример 4. Решите неравенство \(\frac<2+\log_3 x>\gt \frac<6><2x-1>\)

Разобьем неравенство на совокупность двух систем.
Если \(x\gt 1\), то \(x-1\gt 0\), на него можно умножить слева и справа и не менять знак.
Если \(x\lt 1\), то \(x-1\lt 0\), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: \(x\gt 0\)

Получаем совокупность: \begin \left[ \begin \begin x\gt 1\\ 2+\log_3 x\gt\frac<6(x-1)> <2x-1>\end \\ \begin 0\lt x\lt 1\\ 2+\log_3 x\lt\frac<6(x-1)> <2x-1>\end \end \right. \\ 2+\log_3 x\gt \frac<6(x-1)><2x-1>\Rightarrow \log_3 x\gt \frac<6(x-1)-2(2x-1)><2x-1>\Rightarrow \log_3 x\gt \frac<2x-4><2x-1>\\ \left[ \begin \begin x\gt 1\\ \log_3 x\gt\frac<2x-4> <2x-1>\end \\ \begin 0\lt x\lt 1\\ \log_3 x\lt\frac<2x-4> <2x-1>\end \end \right. \end Исследуем функцию \(f(x)=\frac<2x-4><2x-1>=\frac<2x-1-3><2x-1>=1-\frac<3><2x-1>\)
Точка разрыва: \(x=\frac12\) – вертикальная асимптота
Односторонние пределы: \begin \lim_\left(1-\frac<3><2x-1>\right)=1-\frac<3><-0>=+\infty\\ \lim_\left(1-\frac<3><2x-1>\right)=1-\frac<3><+0>=-\infty \end Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: \(y=1\) \begin \lim_\left(1-\frac<3><2x-1>\right)=1-\frac<3><-\infty>=1+0\\ \lim_\left(1-\frac<3><2x-1>\right)=1-\frac<3><+\infty>=1-0 \end На минус бесконечности кривая стремится к \(y=1\) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=\left(1-\frac<3><2x-1>\right)’=\frac<3><(2x-1)^2>\gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-\frac<6> <(2x-1)^3>$$ Одна критическая точка 2-го порядка \(x=\frac12\)

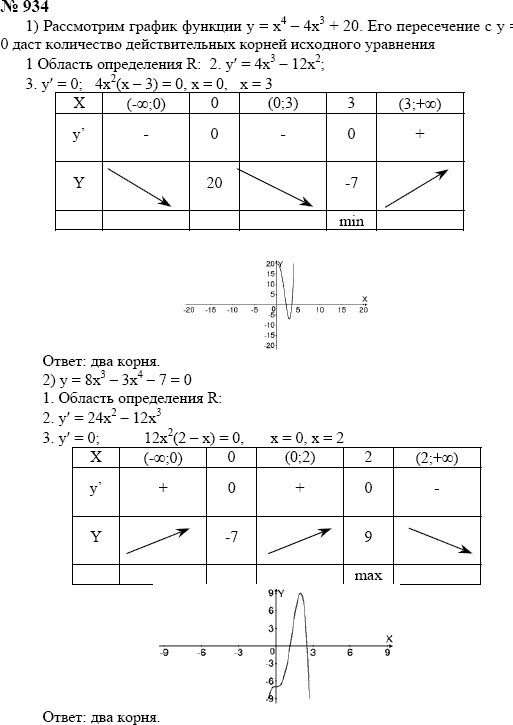
Найдем число действительных корней. ГДЗ 10 класс Алгебра Алимов Упр 934 параграф 51

Доброго дня! А давайте вместе решим?)
Найти число действительных корней уравнения:
1) х4 — 4х8 + 20 = 0;
2) 8х3 — Зх4 — 7 = 0.

Решили уже!

Не понимаю, как решить задачу Гл.V №441.
Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.
( Подробнее. )

Доброго дня! Построим график функций?
1) у = x3 — Зх2 + 4;
3) у = -х3 + 4×2 — 4х; ( Подробнее. )

Что это за мнемоническое правило?

Что такое логарифм?

Докажите, что при осевой симметрии плоскости:
а) прямая, параллельная оси симметрии, отображается на прямую, параллельную оси ( Подробнее. )