Определить геометрическое место точки по уравнению

Геометрические места точек

Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.

Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.

Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .

Определить геометрическое место точки по уравнению

Древнеегипетскую и вавилонскую культуру в области математики продолжали греки. Они не только усвоили весь опыт их геометрии, но и пошли гораздо дальше. Ученые древней Греции сумели привести в систему накопленные геометрические знания и, таким образом, заложить начала геометрии как дедуктивной науки.

Греческие купцы познакомились с восточной математикой, прокладывая торговые пути. Но люди Востока почти не занимались теорией, и греки быстро это обнаружили. Они задавались вопросами: почему в равнобедренном треугольнике два угла при основании равны; почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах?

К сожалению, не сохранилось первоисточников, описывающих ранний период развития греческой математики. Только благодаря восстановленным текстам четвертого столетия до нашей эры и трудам арабских ученых, которые были богаты переводами сочинений авторов античной Греции, мы располагаем изданиями Евклида, Архимеда, Аполлония и других великий людей. Но в этих произведениях уже представлена вполне развитая математическая наука.

Математика древней Греции прошла длительный и сложный путь развития, начиная с VI столетия до н.э. и по VI век. Историки науки выделяют три периода ее развития в соответствии с характером знаний:

1. Накопление отдельных математических фактов и проблем (6 — 5B.B. до н.э.).
2. Систематизация полученных знаний (4 — 3 в.в. до н.э.).
3. Период вычислительной математики (3в. до н.э. — 6 в.).

Геометрическое место точек (ГМТ).

Определения.

Геометрическое место – термин, применявшийся в старой литературе по геометрии и до сих пор применяющийся в учебной литературе, для обозначения множества точек, удовлетворяющих некоторому условию, как правило, геометрического характера. Например: геометрическое место точек, равноудаленных от двух данных точек A и B – это серединный перпендикуляр к отрезку AB. Иногда говорят и о геометрическом месте прямых и других фигур.

Название связано с представлением о линии как о «месте», на котором располагаются точки.

Геометрическое Место Точек (ГМТ) — в геометрии траектория некоторой точки, перемещающейся в соответствии с данной формулой или условием. Например, круг является геометрическим местом точки, перемещающейся на плоскости так, что расстояние от места ее нахождения до центра остается неизменным.

Геометрическое место точек (ГМТ) — это множество точек, в которое попадают все точки, удовлетворяющие определенному условию, и только они.

Геометрическое место точек (ГМТ) — фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством.

Примеры.

• Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от концов отрезка.
• Окружность есть геометрическое место точек, равноудалённых от данной точки, называемой центром окружности.
• Парабола есть геометрическое место точек, равноудалённых от точки (называемой фокусом) и прямой (называемой директрисой).

Пример 1.

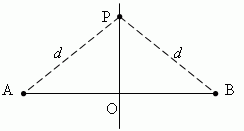
Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO перпендикулярно AB и AO = OB :

Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d .

Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.

Пример 2.

Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон.

Пример 3.

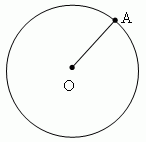
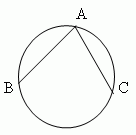
Окружность есть геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра ( на рис. показана одна из этих точек – А ).

Окружность

Теоретическая часть.

Окружность — это геометрическое место точек (т.е. множество всех точек) на плоскости, равноудалённых от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности ( AmB, рис.1 ) называется дугой. Прямая PQ, проходящая через точки M и N окружности ( рис.1 ), называется секущей, а её отрезок MN, лежащий внутри окружности — хордой.

рис. 1

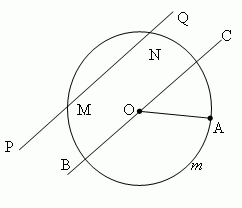
Хорда, проходящая через центр круга ( например, BC, рис 1), называется диаметром и обозначается d или D . Диаметр – это наибольшая хорда, равная двум радиусам (d = 2 r).

Касательная. Предположим, секущая PQ ( рис.2 ) проходит через точки K и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K. Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K. По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.

рис. 2

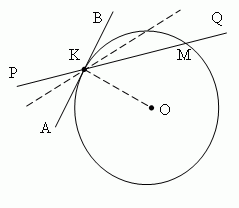
1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания ( AB перпендикулярно OK, рис.2 ).
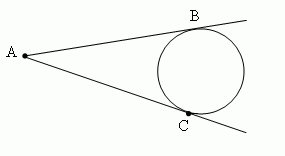
2. Из точки, лежащей вне круга, можно провести две касательные к одной и той же окружности; их отрезки равны АВ=АС ( рис.3 ).

рис. 3

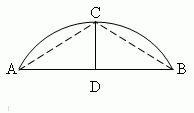
Сегмент – это часть круга, ограниченная дугой ACB и соответствующей хордой AB ( рис.4 ). Длина перпендикуляра CD, проведенного из середины хорды AB до пересечения с дугой ACB, называется высотой сегмента.

рис. 4
Сектор – это часть круга, ограниченная дугой AmB и двумя радиусами OA и OB, проведенными к концам этой дуги ( рис.5 ).

Центральный угол – угол, образованный двумя радиусами ( ∠AOB, рис.5 ). Вписанный угол – угол, образованный двумя хордами AB и AC, проведенными из их одной общей точки ( ∠BAC, рис.4 ). Описанный угол – угол, образованный двумя касательными AB и AC, проведенными из одной общей точки ( ∠BAC, рис.3 ).

рис. 6

Соотношения между элементами круга.

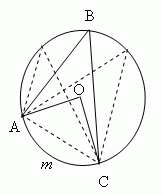
Вписанный угол ( ∠ABC, рис.7 ) равен половине центрального угла, опирающегося на ту же дугу AmC ( ∠AOC, рис.7 ). Поэтому, все вписанные углы ( рис.7 ), опирающиеся на одну и ту же дугу ( AmC, рис.7 ), равны. А так как центральный угол содержит то же количество градусов, что и его дуга ( AmC, рис.7 ), то любой вписанный угол измеряется половиной дуги, на которую он опирается ( в нашем случае AmC ).

рис. 7

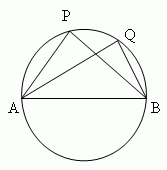
Все вписанные углы, опирающиеся на полукруг (∠APB, ∠AQB, …, рис.8 ), прямые.

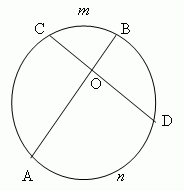
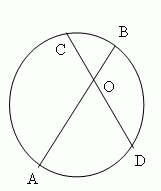
Угол (∠AOD, рис.9 ), образованный двумя хордами ( AB и CD ), измеряется полусуммой дуг, заключённых между его сторонами: ( AnD + CmB ) / 2 .

рис. 8 рис. 9

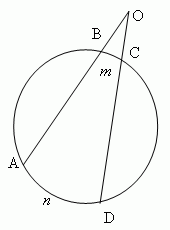
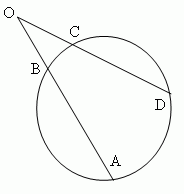
Угол (∠AOD, рис.10), образованный двумя секущими ( AO и OD ), измеряется полуразностью дуг, заключённых между его сторонами: ( AnD – BmC ) / 2.

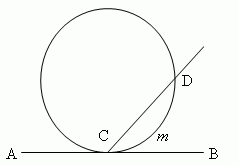
Угол (∠DCB, рис.11), образованный касательной и хордой ( AB и CD ), измеряется половиной дуги, заключённой внутри него: CmD / 2.

Угол (∠BOC, рис.12), образованный касательной и секущей ( CO и BO ), измеряется полуразностью дуг, заключённых между его сторонами: ( BmC – CnD ) / 2 .

рис. 10 рис. 11

Описанный угол (∠AOC, рис.12), образованный двумя касательными ( CO и AO ), измеряется полуразностью дуг, заключенных между его сторонами: ( ABC – CDA ) / 2 .

Произведения отрезков хорд ( AB и CD, рис.13 или рис.14), на которые они делятся точкой пересечения, равны: AO · BO = CO · DO.

Квадрат касательной равен произведению секущей на её внешнюю часть ( рис.12): OA 2 = OB · OD. Это свойство можно рассматривать как частный случай рис.14.

рис. 13 рис. 14

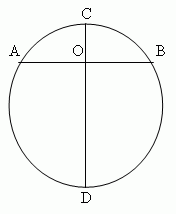
Хорда ( AB , рис.15), перпендикулярная диаметру ( CD ), O пополам: AO = OB .

рис. 15

Интересный факт:

Поздравляем с Пи-раздником вас.

Выражаясь научным языком, число «Пи» — это отношение длины окружности к ее диаметру. Простая вроде бы вещь, но волнует умы математиков с глубокой древности. И продолжает волновать. До такой степени, что ученые — лет 20 назад — договорились отмечать праздник этого числа. И призвали присоединиться к торжествам всю прогрессивную общественность. Она присоединяется: ест круглые Пи-роги, вы-ПИ-вает, обязательно Пи-во и издает звуки Пи при встрече.

Фанаты будут соревноваться, вспоминая знаки числа «Пи». И постараются превзойти рекорд 24-летнего китайского студента Лю Чао, который назвал по памяти без ошибок 68890 знаков. На это у него ушло 24 часа и 4 минуты.

Отправление торжеств назначено на 14 марта — дату, которая в американском написании выглядит как 3.14 — то есть, первыми тремя цифрами числа «Пи».
По легенде, о числе «Пи» знали еще вавилонские жрецы. Использовали при строительстве Вавилонской башни. Но не смогли точно вычислить его значение и от этого не справились с проектом. Сам символ числа «Пи» впервые использовал в своих трудах в 1706 году математик Уильям Джон (William Jones). Но реально он прижился после 1737 года благодаря стараниям шведского математика Леонарда Эйлера (Leonhard Euler).

Отмечать праздник придумал американский физик Ларри Шо (Larry Shaw).
На вопрос, сколько знаков в числе «Пи» после запятой, точного ответа нет. Скорее всего, их бесконечное число. А главная особенность в том, что последовательность этих знаков не повторяется. Сегодня их известно 12411 триллионов. Обследовано 500 миллиардов. И повторений не найдено.

Как считают некоторые видные физики и математики, например Дэвид Бейли, Питер Борвин и Саймон Плофе (David Bailey, Peter Borewin, Simon Plouffe), их — повторений — не найти никому и никогда. Хоть испиши знаками всю Вселенную. Да хоть сколько Вселенных. И в этом ученые видят некую скрытую мистику. Полагают, что в числе «Пи» зашифрован бесконечный первородный хаос, ставший потом гармонией. Или какая-то загадочная информация.

1. Сформулируйте определение окружности и круга?
2. С какими новыми понятиями вы познакомились?
3. Что называется геометрическим местом точек?
4. Какая разница между диаметром и радиусом?
5. Как найти радиус окружности какая описана около треугольника?

Список использованных источников:

1. Урок на тему «Наглядная геометрия» Автор: Самылина Марина Валентиновна., г. Киев
2. Савин А.П. Метод геометрических мест /Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. Сост. И.Л. Никольская. – М.: Просвещение, с. 74.
3. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 84.
4. Шарыгин И.Ф. Геометрия. 7-9 классы: Учебник для общеобразовательных учебных заведений. – М.: Дрофа, с. 76.
5. Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Определить геометрическое место точки по уравнению

Задание 5. Изобразить геометрическое место точек, заданных уравнением

б) в пространстве

Решение. а) Данное уравнение есть общее уравнение кривой второго порядка. Методом выделения полного квадрата приведём его к каноническому виду:

Это уравнение эллипса с центром в точке . Ось по Х равна ось по У равна

В пространстве заданному уравнению соответствует эллиптический цилиндр, направляющей линией которого является полученный в пункте а) эллипс. Направляющая расположена в плоскости Oxy, а образующие – прямые, параллельные оси Oz