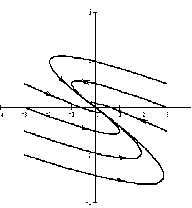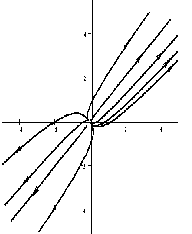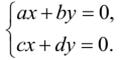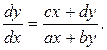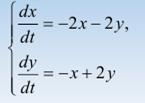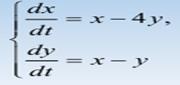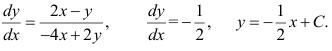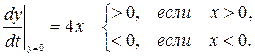Определить характер точек покоя системы уравнений

2.1 Точки покоя системы дифференциальных уравнений

(2.1)

Если точка удовлетворяет условиям , то

Есть решение рассматриваемой системы, при этом точку называют точкой покоя этой системы.

Будем рассматривать однородную систему двух линейных уравнений с постоянными коэффициентами

(2.2)

Точка , очевидно, точка покоя этой системы. Составим характеристический определитель системы

Его корни определяют вид решений и устойчивость точки покоя. Если корни имеют отрицательные вещественные части, то точка покоя устойчива асимптотически.

Если корни чисто мнимые, т. е. , то точка покоя устойчива, но не асимптотически.

Если хотя бы один корень имеет положительную вещественную часть , то точка покоя неустойчива. Если один корень нулевой, а другой отрицательный, то точка покоя устойчива, но не асимптотически. Если два нулевых корня, то точка может быть как устойчивой не асимптотически, так и неустойчивой.

Наиболее наглядно устойчивость и неустойчивость точки покоя проявляется при рассмотрении фазовых траекторий системы (2.2).

Фазовая траектория системы (2.2) есть кривая на плоскости , задаваемая функциями есть решение системы (2.2). На этой кривой обычно стрелками указывают движение точки при возрастании . В зависимости от корней характеристического уравнения различают следующие точки покоя:

1) если корни вещественные отрицательные, то точку покоя называют устойчивым узлом (рис. 2.2).

2) если корни вещественные положительные, точку покоя называют неустойчивым узлом (рис. 2.3).

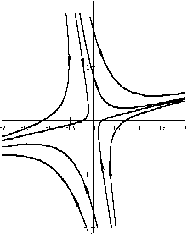
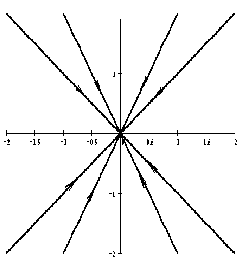
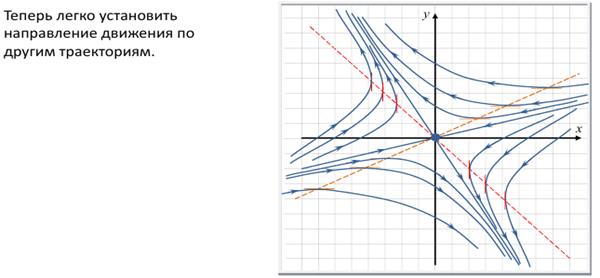
3) Если корни вещественные разного знака, то точку покоя называют седлом (рис. 2.4).

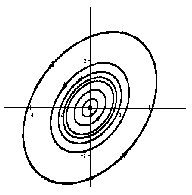
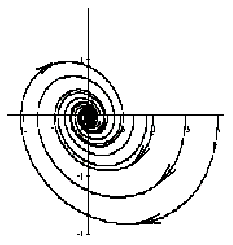
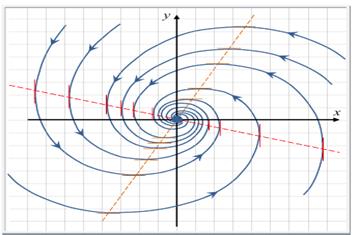
4) Если корни комплексные, то при положительных вещественных частях точка покоя есть неустойчивый фокус, при отрицательных – устойчивый фокус (рис. 2.5 и 2.6 соответственно).

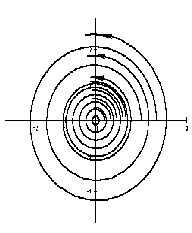
5) Если корни чисто мнимые, то точка покоя называется центром (устойчива не асимптотически) (рис. 2.7).

Фазовые траектории вблизи различных точке покоя показаны на рис. 2.2 – 2.7. следует отметить, что для асимптотически устойчивой точки покоя все фазовые траектории при стремятся к началу координат. В случае неасимптотической устойчивости (центр) фазовые траектории для всех находятся в ограниченной окрестности начала координат. Для неустойчивой точки покоя существуют траектории, начинающиеся сколь угодно близко к началу и со временем неограниченно удаляющиеся.

Определить характер точек покоя системы уравнений

ТОЧКИ ПОКОЯ АВТОНОМНОЙ СИСТЕМЫ 2-ГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

Высшая математика

Рассмотрим линейную автономную систему 2-го порядка с постоянными коэффициентами x‘ = A·x :

Такая система имеет единственную точку покоя x ≡ 0, x=0, y=0, (0, 0).

Характер точки покоя (её устойчивость, асимптотическую устойчивость, неустойчивость) можно установить по собственным значениям λ₁, λ₂ матрицы системы A.

Если λ₁, λ₂ — разные действительные отрицательные числа , то точка покоя асимптотически устойчива, такая точка покоя называется устойчивый узел .

На рисунке приведен фрагмент фазового портрета в окрестности устойчивого узла.

Если λ₁, λ₂ — разные действительные положительные числа , то точка покоя неустойчива, такая точка покоя называется неустойчивый узел .

На рисунке приведен фрагмент фазового портрета в окрестности неустойчивого узла.

Если λ₁, λ₂ — действительные числа разных знаков , то точка покоя неустойчива, такая точка покоя называется седло .

На рисунке приведен фрагмент фазового портрета в окрестности седла.

Если λ₁, λ₂ — комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ ≤ 0 , то точка покоя устойчива .

Если λ₁, λ₂ — комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ = 0 , то точка покоя устойчива, но не асимптотически устойчива, такая точка покоя называется центром .

На рисунке приведен фрагмент фазового портрета в окрестности центра.

Если λ₁, λ₂ — комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ , то точка покоя асимптотически устойчива, такая точка покоя называется устойчивым фокусом .

На рисунке приведен фрагмент фазового портрета в окрестности устойчивого фокуса.

Если λ₁, λ₂ — комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ > 0 , то точка покоя неустойчива, такая точка покоя называется неустойчивым фокусом .

На рисунке приведен фрагмент фазового портрета в окрестности неустойчивого фокуса.

Если λ₁= λ₂ ≠ 0 — действительные положительные числа , то точка — узел специального вида — диакритический узел ;

На рисунке приведен фрагмент фазового портрета в окрестности устойчивого диакритического узла.

Если λ₁= 0, λ₂ ≠ 0, то существует прямая, проходящая через начало координат, все точки которой являются точками покоя.

Если λ₁= λ₂ = 0, то все точки плоскости являются точками покоя системы.

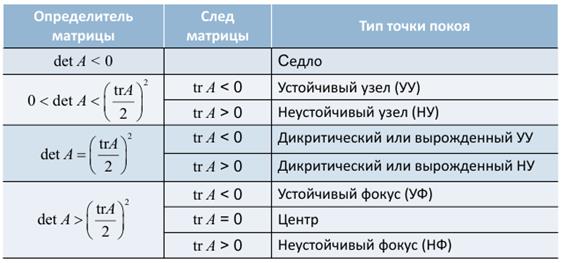
Правила определения типа точки покоя

Можно определить тип точки покоя и характер ее устойчивости, не находя собственных значений матрицы системы (1), а зная только ее след tr A и определитель det A.

Классификация особых точек линейных двумерных систем

Алгоритм построения фазового портрета ЛДС

1.Определить положения равновесия, решив систему уравнений:

2. Найти собственные значения матрицы системы, решив характеристическое уравнение:

3. Определить тип точки покоя и сделать вывод об устойчивости.

4. Найти уравнения главных изоклин горизонтальной и вертикальной, и построить их на фазовой плоскости.

5. Если положение равновесия является седлом или узлом, найти те фазовые траектории, которые лежат на прямых, проходящих через начало координат.

6. Нарисовать фазовые траектории.

7. Определить направление движения по фазовым траекториям, указав его стрелками на фазовом портрете.

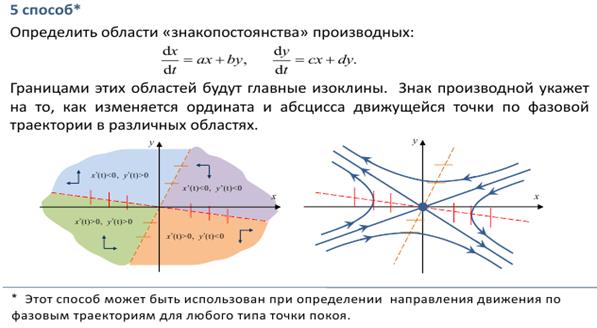
Заметим, что точка покоя на фазовой плоскости это пересечение главных изоклин. Вертикальную изоклину на фазовой плоскости будем помечать вертикальными штрихами, а горизонтальную горизонтальными.

Фазовые траектории

Если положение равновесия является седлом или узлом, то существуют фазовые траектории, которые лежат на прямых, проходящих через начало координат.

Уравнения таких прямых можно искать в виде y = kx. Подставляя y = k x в уравнение:

для определения k получим:

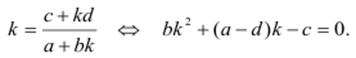(4)

(Уравнения прямых, содержащих фазовые траектории, можно искать и в виде x = ky . Тогда для нахождения коэффициентов следует решить уравнение

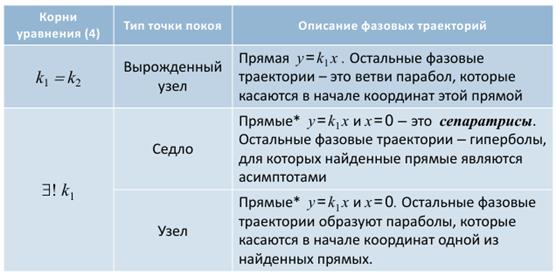
Дадим описание фазовых траекторий в зависимости от количества и кратности корней уравнения (4).

* Если уравнения прямых ищутся в виде x = ky, тогда это будут прямые x= k₁ y и y = 0.

Если положение равновесия является центром, то фазовые траектории являются эллипсами.

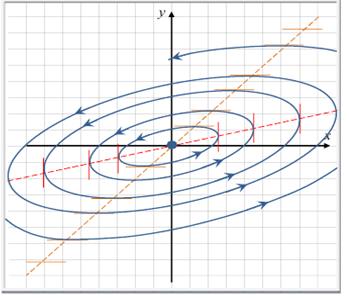
Если положение равновесия является фокусом, то фазовые траектории являются спиралями.

В случае, когда ЛДС имеет прямую точек покоя, то можно найти уравнения всех фазовых траекторий, решив уравнение:

Его первый интеграл ax + by = C и определяет семейство фазовых прямых.

Если положение равновесия является узлом или фокусом, то направление движения по фазовым траекториям определяется однозначно его устойчивостью (к началу координат) или неустойчивостью (от начала координат).

Правда, в случае фокуса требуется установить еще и направление закручивания (раскручивания), спирали по часовой или против часовой стрелки. Это можно сделать, например, так. Определить знак производной y′(t) в точках оси x.

Когда 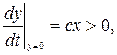если x > 0, то ордината движущейся точки по фазовой траектории при пересечении «положительного луча оси » возрастает.

Значит «закручивание (раскручивание)» траекторий происходит против часовой стрелки.

Когда если x > 0, то «закручивание (раскручивание)» траекторий происходит по часовой стрелки.

Если положение равновесия является центром, то направление движения по фазовым траекториям (по часовой стрелке или против) можно определить так же, как устанавливается направление «закручивания (раскручивания)» траектории в случае фокуса.

Следовательно, если положение равновесия седло, то достаточно установить направление движения по какой-нибудь траектории. И далее можно однозначно установить направление движения по всем остальным траекториям.

Направление движения (седло)

Чтобы установить направление движения по фазовым траекториям в случае седла, можно воспользоваться одним из следующих способов:

Определить, какая из двух сепаратрис соответствует отрицательному собственному значению. Движение по ней происходит к точке покоя.

Определить, как изменяется абсцисса движущейся точки по любой из сепаратрис. Например, для y = k₁x имеем:

Если x(t) → 0 при t → +∞, то движение по сепаратрисе y = k₁x происходит к точке покоя.

Если x(t) → ±∞ при t→+∞, то движение происходит от точки покоя.

Если ось x не является сепаратрисой, определить как изменяется ордината движущейся точки по фазовой траектории при пересечении оси x.

Когда 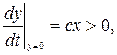если x > 0,то ордината точки возрастает и, значит, движение по фазовым траекториям, пересекающим положительную часть оси x, происходит снизу вверх. Если же ордината убывает, то движение будет происходить сверху вниз.

Если определять направление движение по фазовой траектории, пересекающей ось y, то лучше анализировать изменение абсциссы движущейся точки.

Пример 1.

1. Система имеет единственное нулевое положение равновесия, так как

2. Построив соответствующее характеристическое уравнение l 2 – 6 = 0, найдем его корни l_1,2 = ± Ö6. Корни вещественные и разного знака. Следовательно, положение равновесия седло.

Найдем корни характеристического уравнения, или собственные значения, системы уравнений с помощью функции eig.

3. Сепаратрисы седла ищем в виде y = kx.

4. Вертикальная изоклина: x + y = 0.

Горизонтальная изоклина: x + 2y = 0.

Пример 2.

1. Система имеет единственное нулевое положение равновесия, так как det A = 10 ≠ 0.

2. Построив соответствующее характеристическое уравнение l 2 + 7l + 10 = 0,

найдем его корни l₁ = 2, l₂ = 5. Следовательно, положение равновесия неустойчивый узел.

4. Вертикальная изоклина: 2x + y = 0.

Горизонтальная изоклина: x + 3y = 0.

Найдем собственные вектора матрицы А:

Т.е., собственные значения l₁ = 5 и l₂ = 2.

Так как l₂ = 2 является меньшим по абсолютной величине собственным значением, найдем соответствующий ему собственный вектор:

Следовательно, остальные фазовые траектории, образующие параболы, касаются в начале координат прямой y = –x.

Неустойчивость положения равновесия однозначно направление движения – от точки покоя.

Пример 3.

1. Система имеет единственное нулевое положение равновесия, так как det A = 18 ≠ 0.

2. Построив соответствующее характеристическое уравнение l 2 + 3l + 18 = 0,

найдем его дискриминант D = 63. Так как D > a=[-1 -4;4 -2];

3. Вертикальная изоклина: x + 4y = 0.

Горизонтальная изоклина: 2x – y = 0.

Фазовые траектории являются спиралями, движение по которым происходит к началу координат. Направления «закручивания траекторий» можно определить следующим образом.

Определим знак производной y′(t) в точках оси x. При y = 0 имеем:

если x > 0.

Таким образом, ордината движущейся точки по фазовой траектории при пересечении «положительного луча оси x» возрастает.

Значит, «закручивание» траектории происходит против часовой стрелки.

Пример 4.

1. Система имеет единственное нулевое положение равновесия, так как det A = 3 ≠ 0.

2. Построив соответствующее характеристическое уравнение l 2 +3 = 0, найдем его корни l_1,2 = ±iÖ3. Следовательно, положение равновесия центр.

3. Вертикальная изоклина: x – 4y = 0.

Горизонтальная изоклина: x – y = 0.

Фазовые траектории системы эллипсы.

Направление движения по ним можно установить, например, так.

Определим знак производной y′(t) в точках оси x. При y = 0 имеем:

если x > 0.

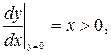
Таким образом, ордината движущейся точки по фазовой траектории при пересечении «положительного луча оси x» возрастает.

Значит, движение по эллипсам происходит против часовой стрелки.

Пример 5.

Так как определитель матрицы системы det A = 0, то система имеет бесконечно много положений равновесия. Все они лежат на прямой y = 2x.

Построив соответствующее характеристическое уравнение l 2 + 5l = 0,

Следовательно, все положения равновесия устойчивы по Ляпунову.

Построим уравнения остальных фазовых траекторий:

Таким образом, фазовые траектории лежат на прямых

Пример 6.

Так как определитель матрицы системы det A = 0, то система имеет бесконечно много положений равновесия. Все они лежат на прямой y = 2x.

Так как и след матрицы системы trA=0, то корни характеристического уравнения l₁ = l₂ = 0.

Следовательно, все положения равновесия неустойчивы.

Построим уравнения остальных фазовых траекторий:

Таким образом, фазовые траектории лежат на прямых y = 2x + C, C – const, и параллельны прямой точек покоя.

Установим направление движения по траекториям следующим образом.

Определим знак производной y′(t) в точках оси x. при y = 0 имеем:

Таким образом, ордината движущейся точки по фазовой траектории при пересечении «положительного луча оси x» возрастает, а «отрицательного» – убывает.

Значит, движение по фазовым траекториям правее прямой точек покоя будет снизу вверх, а левее – сверху вниз.