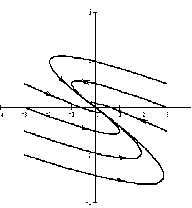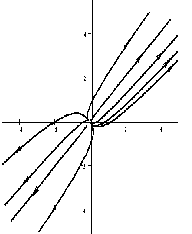Определить характер точки покоя для системы дифференциальных уравнений

ТОЧКИ ПОКОЯ АВТОНОМНОЙ СИСТЕМЫ 2-ГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

Высшая математика

Рассмотрим линейную автономную систему 2-го порядка с постоянными коэффициентами x‘ = A·x :

Такая система имеет единственную точку покоя x ≡ 0, x=0, y=0, (0, 0).

Характер точки покоя (её устойчивость, асимптотическую устойчивость, неустойчивость) можно установить по собственным значениям λ₁, λ₂ матрицы системы A.

Если λ₁, λ₂ — разные действительные отрицательные числа , то точка покоя асимптотически устойчива, такая точка покоя называется устойчивый узел .

На рисунке приведен фрагмент фазового портрета в окрестности устойчивого узла.

Если λ₁, λ₂ — разные действительные положительные числа , то точка покоя неустойчива, такая точка покоя называется неустойчивый узел .

На рисунке приведен фрагмент фазового портрета в окрестности неустойчивого узла.

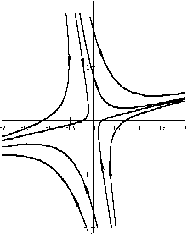
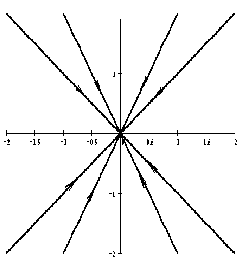
Если λ₁, λ₂ — действительные числа разных знаков , то точка покоя неустойчива, такая точка покоя называется седло .

На рисунке приведен фрагмент фазового портрета в окрестности седла.

Если λ₁, λ₂ — комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ ≤ 0 , то точка покоя устойчива .

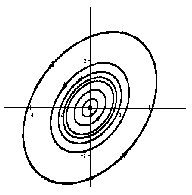
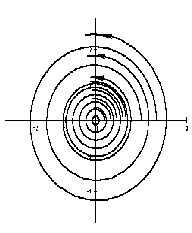
Если λ₁, λ₂ — комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ = 0 , то точка покоя устойчива, но не асимптотически устойчива, такая точка покоя называется центром .

На рисунке приведен фрагмент фазового портрета в окрестности центра.

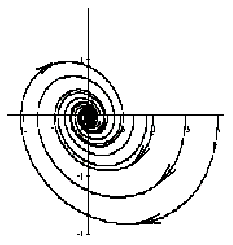
Если λ₁, λ₂ — комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ , то точка покоя асимптотически устойчива, такая точка покоя называется устойчивым фокусом .

На рисунке приведен фрагмент фазового портрета в окрестности устойчивого фокуса.

Если λ₁, λ₂ — комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ > 0 , то точка покоя неустойчива, такая точка покоя называется неустойчивым фокусом .

На рисунке приведен фрагмент фазового портрета в окрестности неустойчивого фокуса.

Если λ₁= λ₂ ≠ 0 — действительные положительные числа , то точка — узел специального вида — диакритический узел ;

На рисунке приведен фрагмент фазового портрета в окрестности устойчивого диакритического узла.

Если λ₁= 0, λ₂ ≠ 0, то существует прямая, проходящая через начало координат, все точки которой являются точками покоя.

Если λ₁= λ₂ = 0, то все точки плоскости являются точками покоя системы.

2.1 Точки покоя системы дифференциальных уравнений

(2.1)

Если точка удовлетворяет условиям , то

Есть решение рассматриваемой системы, при этом точку называют точкой покоя этой системы.

Будем рассматривать однородную систему двух линейных уравнений с постоянными коэффициентами

(2.2)

Точка , очевидно, точка покоя этой системы. Составим характеристический определитель системы

Его корни определяют вид решений и устойчивость точки покоя. Если корни имеют отрицательные вещественные части, то точка покоя устойчива асимптотически.

Если корни чисто мнимые, т. е. , то точка покоя устойчива, но не асимптотически.

Если хотя бы один корень имеет положительную вещественную часть , то точка покоя неустойчива. Если один корень нулевой, а другой отрицательный, то точка покоя устойчива, но не асимптотически. Если два нулевых корня, то точка может быть как устойчивой не асимптотически, так и неустойчивой.

Наиболее наглядно устойчивость и неустойчивость точки покоя проявляется при рассмотрении фазовых траекторий системы (2.2).

Фазовая траектория системы (2.2) есть кривая на плоскости , задаваемая функциями есть решение системы (2.2). На этой кривой обычно стрелками указывают движение точки при возрастании . В зависимости от корней характеристического уравнения различают следующие точки покоя:

1) если корни вещественные отрицательные, то точку покоя называют устойчивым узлом (рис. 2.2).

2) если корни вещественные положительные, точку покоя называют неустойчивым узлом (рис. 2.3).

3) Если корни вещественные разного знака, то точку покоя называют седлом (рис. 2.4).

4) Если корни комплексные, то при положительных вещественных частях точка покоя есть неустойчивый фокус, при отрицательных – устойчивый фокус (рис. 2.5 и 2.6 соответственно).

5) Если корни чисто мнимые, то точка покоя называется центром (устойчива не асимптотически) (рис. 2.7).

Фазовые траектории вблизи различных точке покоя показаны на рис. 2.2 – 2.7. следует отметить, что для асимптотически устойчивой точки покоя все фазовые траектории при стремятся к началу координат. В случае неасимптотической устойчивости (центр) фазовые траектории для всех находятся в ограниченной окрестности начала координат. Для неустойчивой точки покоя существуют траектории, начинающиеся сколь угодно близко к началу и со временем неограниченно удаляющиеся.

Простейшие типы точек покоя

Пусть имеем систему двух линейных однородных дифференциальных уравнений с постоянными коэффициентами причем

Точка , в которой правые части уравнений системы (1) обращаются в ноль, называется точкой покоя системы (1).

Для исследования точки покоя системы (1) надо составить характеристическое уравнение

и найти его корни и .

Возможны следующие случаи.

1. Корни характеристического уравнения (2) вещественные и разные:

а) . Точка покоя асимптотически устойчива (устойчивый узел, рис. 32);

б) 0,\,\lambda_2>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAH4AAAATCAMAAABhl0k+AAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMWHQwCEQA0GageBx8LFRDpCt4AAAAbhJREFUSMfFVldyxCAMpUei6v6nDQZcFsvZkMwk/vDs2KxeUbMQ/34p493KeQnMQzRlJYYDefyOhAvgOmNQ9+eG5ILigKiP8yl8/5/BVwp0N6AsaICNqg+750isc8i4rMhuUs39Da8BuMRmXW+Wdg8ly/zDorkRyNTvt6AfDxqUQTs/o8ae8uFoYk2qBPSUZt3gPeO+fHIfZgIw4A+7kJR4IOBfCdAj/JOGRuDFRiB/hup1M4xgqtd5fcnfDs/QHRosMNTkNY8zvAyhJdNnYps0av9evdJNA2DJxn1ZSNDTtMPLVCLFRpz4Nj3hwxO80k5vGkwULsV7jFpGZcp9GuiqdoHuL96Zb6jf52qOSYqmwSDXl/Y6Fd2ANx0dWytZFr6Cq6uVsff9VrSXuVnzLsWuoYaf1MPUwbr3fWzouY8TZODvjeeSHxND0mnBqLquQXg9Nx4wsysm25i4c2i9wltuj1SzlN6o2nAUgByN0GtK4dWuwowdgSGOxWHHWQtuhs/A9oGKw3V/vN/TIOXWY1XZxXfLBbGxOG4XrGzNzO1paQCK/9HmN5rMwt5ijwaql/qDzxR0vw7xCYY/D3jyG++NAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />. Точка покоя неустойчива (неустойчивый узел, рис. 33);

в) 0,\,\lambda_2 . Точка покоя неустойчива (седло, рис. 34).

2. Корни характеристического уравнения (2) комплексные:

а) . Точка покоя асимптотически устойчива (устойчивый фокус, рис.35);

q\ne0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGoAAAAVCAMAAACZi4uxAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAYSHAEJnpQYEB0DHBcbFSUNy43AAAAbpJREFUSMfVVcmShCAMFQKBsJn//9phUTvYdpfW1ByGg5ZWyPMtxGX570v/arN7sF0X+RQdPUGy6JM1d6uLE0BoLaonSBUm2ZvVTpAy6Cscu6s6r97p9vpF8U0NQdRlblqEclVnfMhnpVbO7WP5ng5Osk9MxzVCMdGC6GJU8DOY7wI49m9tFZTo8vwuCVKEG1RrEAwGawzKelLB6guodFYAQt3JeU9aXwraddtO/IKqbBGbvmGyaAazH6B6WizHTWbfF/ZrnKB6Axdj12UQlWAuHWAfWEVurgDSR6d2KBgRzO1mGJczVLXhBHVKu+W1NZvSRUlfQA2vltIe1lObCiQEVFsC51gQtCC73aohoB367QJu2euVNSPQ8FB/iYXmca7qfi2iCtgZx0XEAtcRDn0w7+cqDMHxdGSoh51m/1vn9k2Bswgm1bkzWaXO50G3aOvRPrMFi04eYf827EwqqoT6miwm8RZKmayi8LZVoc043KlWaU1yMF1OVefH15CRrY1xnL+R6hMh6+04w7O/iZpnQz6suiY1jTf76G9iYOpmApvvpMTAAiiPSK0TJ0gJXj4Hs/zlIrr5n/8Bj3oQCknmmsUAAAAASUVORK5CYII=» style=»vertical-align: middle;» />. Точка покоя неустойчива (неустойчивый фокус, рис.36);

3. Корни кратные:

а) . Точка покоя асимптотически устойчива (устойчивый узел, рис.38, 39);

б) 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGgAAAATBAMAAACO11WQAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQoFewKTnMRAg0CJxkY7DLSgAAAFdSURBVCjPY2AgC/D4YBc/cgC7uDiYjDPAKsn6GKtwWWg6iJoXgFWW8xU2Ue5kBrMNQJrrJXZ3+G2AM6dOgLF4HzDwXQDSzG+wa7JDeIrRtQDKYnNgYFkApDleYdfUl4BgM4YIQBh8QE0PwCEBM4aBXRAMGiAh8RzZLyGQ4NoH02QHdCQnWIhZCQwghjC/ZWBolIDrCgPrkgNqeggyPi2BYdISLIGbxsAZGAYPAg4tAyRNZqWPGTpVMPSwp8cZ8AZwBaBqgvqJ+SHjUwYGFQzn2RnUBfAu4IWFBjdYDyj0uBJAkgxpDVBNSAHB/JiB7QUwEqE2cUdBAoIVGE8BYO/qGTBgOM8ugIEJmJCsGqCBBw1yxocMcgIgfQzzHDA1AZ3MmcLA7gFR6iIAEzc7kwx0EcgcAUxNIH9tZGhpACeLUkSK4jaGhyemJkiIOQoG4M5UJWnOWLPHu3cXGKgEAGUFSl2PiR1zAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />. Точка покоя неустойчива (неустойчивый узел, рис.40, 41).

Пример 1. Определить характер точки покоя (0,0) системы

Решение. Составляем характеристическое уравнение

\lambda_2=3-\sqrt<2>>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAS8AAAAXBAMAAACortSfAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQRGBpGbAgugg0DGRUU3Z2TAAAAPiSURBVEjH7VbdS5NRGH/ed3v30TZZZUE3Mk3Muoih4IUXMi3NLRhvRmQFY2mJGogYfdCFSKVMLFmgoRAiYiB9yAITMYgFEeWF6EW34nTm1Lm/ofPxfu19T2qw7nou9Ow55/zO7/yej/cA/Ld/badHkXlyBofRRnMBxA9mkHXmipcZo6VygWRqKEKWM8VeYrQi9tz5JbY0J5humwdeGJycWyXezD5Fs0Rr1cAfMTg/0HuXrjG31D18y3Jfhfn2pE4w17Pv6rGLImub8K6e5bePw0KH/pyS5id0zwYLydnEp+j5XFTrn+DvQCicvXZkSehXfoyFWXBzMcsuw20VnaIjEs123oJScgn7NgvJsgEdVAarNghCJ5cEWwKNHD8UZxAgrW7cYsF1h01phvsM2PphMY6rQDnFsQvmHoobZWnfBpmYkdghj5AC8zoeHvfLzj6AVnUjMwCzopPlvwd5O1CANbbXyaG2JsC0Q0YhLztdf0np7M5KMbiB1cSWf1NyooUdatFss7O/9DGjwMaBE2GFBJ9/JDGzrIGVhv1sj7LyMDHChGusYRBr0p4xRJk5MDG1HoIxJSgUjgRk+E2MlWJkA2XEV5ZRYqtg3aThQcLxNJwPiJEFpgp/NjG8hPPhUZWs+lCvLG2Hyj4UB36Z8HRROMLoaEDXlewkxTD9pKzf9TKJmIkSC6SBq2eEM4IQXeXlFefKyzH2PFLcgvlzaracem8g5or0wFB+v1EdvAvBISuTM/sK0d+nrCHMFGLm8QjYLQxiiz5y6fsXyKW5dlSL+aT0VXVOYmJ8Vo41zuzCV5g0pmxK0bALN6sgQp/AE5ql12toWZvI1QOexSWQiN0lN8Lj4jhUhbWh5AuR5G1Y+gE4JgG9ei1X5ZRSlAnUTxagHhR9iNzfolwmK8nstjXUe7AuIsRlXl1EKFSVuB+ZB+CzTyamJv/KGlFMm/zTUZJiJTH4IqXYbaWPJUGgWRoSIeKRZNAkf8bLZXShXUe9B/2vlRIXJX+XdDXax1ARIfKGUI74+MFYNrGQD6cYP9XSmshuFwVuLgEhUttCmtSGa0IH1+5xbupaRQQu4w19LdNeyqtBmnkKpUhD1wbpiQZi3GTlc127sG3NYCT0TlklDbZaCV9vowhzJN/zfOSjNOsxfP+C+qdSt4jZ5yE4XOT2gPItnaudxNuxLJ+MxKDwkkdHTNi8qJl3+NXx8DX0h/x24DPcfJOgh/toeKyM9WqpmtVuwv/UZKPF+8cnk/IR5yPhvZ5WmsmS5fwDvBFTB3jVCa19sf1Xdbv3gtBcLZhJ749mT+bsfV6816Tzr+H8e03+BtfBA04k/tP9AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> вещественные, разные, положительные. Следовательно, точка покоя — неустойчивый узел.

Связь между типами точек покоя и значениями корней характеристического уравнения (2) можно представить наглядно. Для этого введем обозначения . Тогда характеристическое уравнение запишется в виде .

Рассмотрим плоскость с прямоугольными декартовыми координатами и и отметим на ней области, соответствующие различным типам покоя (рис. 42). Из приведенной выше классификации следует, что условиями устойчивости точки покоя являются . Они выполняются при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADUAAAARBAMAAACP9fljAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwEURoSHbgmbwMZHLPgtLAAAAy0lEQVQY02NgwA+YF+CWYzmKKcakAKFjjmBKzd4GMczxTAC6XKQCx1QQzTpZxgEswLUVLufDwHAaRHMX6EAtVPSCySUyMIiBaDMDRpiFKkJQxkEGBhkQXc7AdNIAKhYCkeSCyjEnA+kCmGEhGWBnguSAvmAHiutMhrvCPAkmtwBkHQMD43FUOWaomeUgdXALo8FmMkxkYMiEWIewMEQC7j+g2zkmCgJBzmRUP+goMB1iYGA7AwYnwH53gtnKMaOtASUQuVwR7IhWBgYAYb0rVmdybtQAAAAASUVORK5CYII=» /> и 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA0GginYExwEIB4FEh8BGxVXXvTAAAAL9JREFUKM+1kdsOAyEIREURvC///7WV3U1bL0nbh/pgonJkhjHmbysGir/U24SY6Pv6IKFDte3eyJf18oC+NbH73xjdbKCy7sLXMftz0TsSBsDJBYj6biBVBBLk9y7IYbDwAhpAMaWimYbmkHMcAZMU8FU9Mq9eHKa8doiCJ7sFYAPQOSonfi1n+5QUbwDuRLquKRIaTRu+cuhqYrJK5SmJYxyryUKatNolwIPpQ3BdQ7KY7qBLmdS4Xf7OZpX9AFDMBpP54cUeAAAAAElFTkSuQmCC» />, т. е. для точек, которые находятся в первой четверти.

Если и комплексные, то точка покоя будет типа фокуса. Этому условию удовлетворяют точки, которые лежат между ветвями параболы и не принадлежат оси .

Точки полуоси , для которых 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADUAAAARBAMAAACP9fljAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwEURoSHbgmbwMZHLPgtLAAAAy0lEQVQY02NgwA+YF+CWYzmKKcakAKFjjmBKzd4GMczxTAC6XKQCx1QQzTpZxgEswLUVLufDwHAaRHMX6EAtVPSCySUyMIiBaDMDRpiFKkJQxkEGBhkQXc7AdNIAKhYCkeSCyjEnA+kCmGEhGWBnguSAvmAHiutMhrvCPAkmtwBkHQMD43FUOWaomeUgdXALo8FmMkxkYMiEWIewMEQC7j+g2zkmCgJBzmRUP+goMB1iYGA7AwYnwH53gtnKMaOtASUQuVwR7IhWBgYAYb0rVmdybtQAAAAASUVORK5CYII=» />, соответствуют точкам покоя типа центра.

Точки, расположенные вне параболы 4\Delta)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAKcAAAAZBAMAAACm+CPaAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAb6BKEHnXaEQ0AlxkSizG6IAAAK8SURBVEjHtZVBa9RAFMff7KZmAy0kcYngYdmNpWihYWmwailL6mGpIktR97p0tUXsIUSQpfRQeihWpZYiuPQgYhGhXvoZhOq9B08eBFu79ZTP4HuTpMluWpg9+A5DMvnnN/P+82YG4P+FZDui0vc3RJUz905EpWt3VwWVP2FUUDkwL/8RlC7BxDlf3kUPudnAqOGB43Okd3giyZ7dlCbvUVuZDV83ov7sXEqa5cMdUdtOLM7gl5TychEbxS0Gb/JO1F9Nr2lFpVQ6W2TPx7j79lZaSbisFSZ7wQu7leF0Tj5Bq1YZW/YkLqmDbKrKLIK2Zw6D15Ya9m87z3nGz2Kp7tLH9cbTLiFU7fFeqF4j6E3JD0y9GvW/sa/xCU/G1CkLQVJTJ1NZjbvzwLavj5tXeqFTBYQq87DJTWWPafL7tv3NNAOXlclbUU4lgua8AW6q8RWbt76/GPmQr/OgsfIlgl5ahRovS4msrfidkbjyleWQqjsErarMJVN1GnN0un26sLLNw+FKghoO5P7ymkfo4In2K7mebPlHkBMQdB1ghUzN4G/yMQz97smcrN4Hgi7hHH0nhFbL0JiFLuornj1BpSZOgUzNlLAadyDTPOOEWag3PjtsHh83V0NoxYGVbuh9gma+1/ceQg5TlzvkLUILZTCK6fTzprn3yJOJx00lKB4PL9Qks8X3pG6a7hi00RjmeoGnH7zE8NLpQjGARhGMaY1pOpmqINQE5agr+Wj5KX1bw1hpBtDMQT7eA1oyuUYJWibGCJlKJTUB28X4c1xSoO4xZZGkFh6gBvog7b72zjxzCr5fdn0eZMJLdGvsU5IZF7/lH14MlB10C/Nm0vQ5J5mmghYEGdmiYzDh6FBimzJNZaEUjVbFLxzDE9PxrScaclHwZpjr527cEJO1nX6gOTH1Wn/XuCbmKa7TP6ovmlkrqbjpAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, соответствуют точкам покоя типа узла.

Область плоскости , где , содержит точки покоя типа седла.

Исключая особые случаи (прохождение через начало координат), замечаем, что седло может перейти в узел устойчивый или неустойчивый (рис.42). Устойчивый узел может перейти либо в седло, либо в устойчивый фокус. Случай равных корней соответствует границе между узлами и фокусами, т.е. параболе .

Пример 2. Исследовать уравнение упругих колебаний с учетом трения и сопротивления среды (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQBAMAAABNQoq8AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcGe2BFbQSGBMfCxcU2qjNsAAADDSURBVBjTY2AgDYgvxCHB5WyyALtM9wW2HUhcDgs4006A8TGyyprjAlCWiwCjCpDNekkzACLQrA6RYnwkwKgHZK42DVFghkq5CcBlAhi4NjOwPSuGGtMJlmJ/xMCgV8DA9JSB6yXc8kg3IMEKkelTAOo2gMv4Iuypm8DA+DoArgVkGiPQbdpgGdY3DDAXQP3DAPKPiAFjkRMbiqsZ1iWwPweGkY+RafYxEL8IJsHA5jklAeSShQysIHtYEaHD2JbKwAAA/gYrl5lLD9QAAAAASUVORK5CYII=» />)

Решение. Переходим от уравнения (3) к эквивалентной ему системе уравнений

источники:

http://matica.org.ua/metodichki-i-knigi-po-matematike/reshenie-sistem-lineinykh-differentcialnykh-uravnenii-s-postoiannymi-koeffitcientami-ustoichivost-reshenii/2-1-tochki-pokoia-sistemy-differentcialnykh-uravnenii

http://mathhelpplanet.com/static.php?p=prostyeishie-tipy-tochek-pokoya